РОЗВЯЗУВАННЯ НЕРІВНОСТЕЙ З ВИКОРИСТАННЯМ НЕВЯЗКИ , ЗВЕДЕННЯМ ДО РІВНЯНЬ

Про матеріал

РОЗВЯЗУВАННЯ НЕРІВНОСТЕЙ З ВИКОРИСТАННЯМ НЕВЯЗКИ , ЗВЕДЕННЯМ ДО РІВНЯНЬ- цікава науково- дослідницька робота учнів

Перегляд файлу

Міністерство освіти і науки, молоді та спорту України

Головне управління освіти і науки Львівської облдержадміністрації

Львівське територіальне відділення МАН України

Сокальська МАН

Відділення: математика

Секція: прикладна математика

РОЗВЯЗУВАННЯ НЕРІВНОСТЕЙ З ВИКОРИСТАННЯМ НЕВЯЗКИ , ЗВЕДЕННЯМ ДО РІВНЯНЬ

Роботу виконав:

Кровіцький Роман Олегович

учениця 10 класу

Сокальської спеціалізованої

школи №3

Науковий керівник:

Вець Богуслава Теодозіївна

Вчитель математики

Сокальської школи № 3

ЗМІСТ

ВСТУП.........................................................................................................................3

Розділ І

Розвязування нерівностей, зведенням до рівнянь з урахуванням невязки:

Лінійні нерівності з однією змінною……………………………………...5
Системи лінійних нерівностей з однією змінною………………………..8
Квадратні нерівності……………………………………………………...12
Ірраціональні нерівності………………………………………………….16

Розділ ІІ.

Дослідження більш складних нерівностей, структуризація розвязків яких має чітку наочність:

2.1. Показникові нерівності……………………………………………………..20

2.2. Логарифмічні нерівності……………………………………………………22

2.3. Тригонометричні нерівності………………………………………………..27

Висновки…………………………………………………………………………31

Список використаних джерел…………………………………………………..32

ВСТУП

Не в кількості знань полягає освіта,

А в повному розумінні

й майстерному застосуванні

всього того, що знаєш.

Дістверг

Систематизація сучасної науки розширює застосування математичних теорій у наукових дослідженнях.

Математика – наука про абстрактні структури, які розглядають об’єкти досить загальної природи. До предмета її вивчення належать просторові форми і відношення реального світу, які мають такий рівень незалежності від змістової основи, що можуть бути повність абстраговані від неї в поняття, за допомогою яких можна суто логічно розвинути теорію.

Такий підхід у дослідженні математичних закономірностей має значні переваги, оскільки основним методом розвитку математичних теорій є логічний висновок, який спирається на експеримент.

Історично склалося так, що математика виникла з практичних потреб людини, на основі задач поставлених життям, і розвивалася з їх розв’язуванням. Пошуки розв’язків окремих задач спонукали вчених розробляти нові методи досліджень, створювати більш досконалі алгоритми, відкривати невідомі закономірності. Усе це сприяло розвитку математичної науки.

Метою моєї роботи є дослідити розв’язування нерівностей, зведенням до рівнянь, структуризація розв’язків яких має чітку наочність, опанувати алгоритм знаходження комплексних розв’язків.

Об’єктом дослідження є нерівності різних видів: лінійні, квадратні, ірраціональні, показникові, логарифмічні, тригонометричні.

Моя робота актуальна, адже на уроках, факультативах при розв’язуванні нерівностей, можна допуститися помилок при змінюванні знаку нерівності, при знаходженні спільних розв’язків, при врахуванні належності точок до інтервалу, або при побудові множини розв’язків за допомогою комп’ютерних програм. Ще складнішим є знаходження комплексних розв’язків нерівності. Проте задача спрощується, якщо опанувати алгоритм знаходження комплексних розв’язків за допомогою способу нев’язки. Його можна використовувати і під час розв’язування олімпіадних або конкурсних завдань. Таке дослідження розв’язків дає більшу інформацію, ніж традиційно прийнята, оскільки можна дізнатися не тільки, якому інтервалу належать розв’язки, а й на скільки більші або менші відповідні вирази для конкретних значень.

Пропоную звести задачу про розв’язування нерівності до розв’язування рівняння з урахуванням нев’язки r (різниці між лівою і правою частинами рівняння). Це дає змогу структуризувати розв’язки нерівності, вказати, де використовується нерівність , наскільки менше ніж для знайденого x, тобто дорівнює нев’язка r.

Лінійні нерівності з однією змінною

Нерівності з однією змінною багато в чому схожі на рівняння з однією змінною. Традиційно їх розв’язують на основі теорем про рівносильність нерівностей. Але оперування з рівняннями простіше, ніж з нерівностями. Наприклад, коли множать або ділять рівняння на число , не треба враховувати знак множника(дільника), на відміну від нерівностей. Запропонований спосіб нев’язки дозволяє запобігти помилкам такого роду.

Приклад 1. Розв’язати нерівність

Розв’язання

Щоб зрівняти обидві частини нерівності, додамо до лівої(меншої) частини нерівності число :

Використаємо відомий алгоритм розв’язування лінійних рівнянь:

Отриманий розв’язок – це множина значень х, які виражаються формулою якщо :

За допомогою параметра r, який є нев’язкою в даній нерівності, множина розв’язків структурована: кожному становиться у відповідність єдиний розв’язок , який задовольняє дану нерівність. Наприклад, якщо

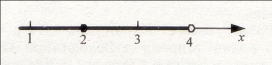
$E:\математика\img037.jpg$

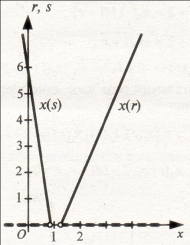
Такі розв’язки отримуємо й без використання нев’язки, але їх структуризація не має чіткої наочності. Тому зобразимо розв’язки, враховуючи те, що х залежить від нев’язки r.

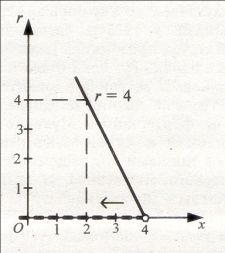
$E:\математика\Originals\img037.jpg$

Коли врахувати, що між розв’язком х та параметром rіснує функціональна залежність , і використати функцію виду , то розв’язок можна зобразити так.

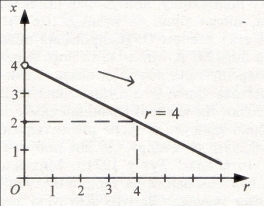
$E:\математика\Originals\Originals\img037.jpg$

Приклад 2. Розв’язати нерівність

Розв’язання

У випадку не строгої нерівності вводимо нев’язку , маємо:

Отже,

Зауваження. Якби в даній нерівності замість знака «» був знак «», то нерівність не мала б жодного розв’язку.

Приклад 3. Розв’язати нерівність

Розв’язання

Введемо нев’язку , маємо:

Значення суперечить умові . Отже, нерівність розв’язків не має.

Системи лінійних нерівностей з однією змінною

Приклад 4. Розв’язати систему нерівностей:

Розв’язання

Дана система рівносильна системі рівнянь і нерівностей:

З рівняння знаходимо:

звідки

Оскільки

Отже,

Міркуючи аналогічно, неважко отримати:

Така відповідь дає більшу інформацію, ніж традиційно прийнята, оскільки можна дізнатися не тільки, якому інтервалу належать значення х, а й на скільки більші або менші відповідні вирази для конкретних значень х. При цьому ще й вказуються верхні межі нев’язок r.

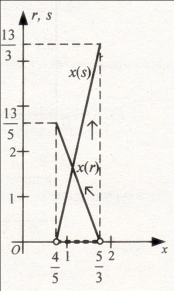
$E:\математика\img038.jpg$

Як бачимо, розв’язки належать інтервалу але вони чітко структуровані для вибраних параметрів або

Приклад 5. Розв’язати систему нерівностей

Розв’язання

Введемо параметри , маємо систему:

звідки отримуємо:

Отже, , якщо , а це суперечить умові Тому розв’язки даної системи відсутні.

$E:\математика\Originals\img038.jpg$

Приклад 6. Розв’язати систему нерівностей

Розв’язання

Введемо параметри , маємо систему:

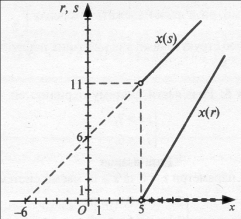
Отже,

Якщо , то параметр s буде завжди додатний, а для параметра s маємо умову

Тому

$E:\математика\img039.jpg$

Квадратні нерівності

Приклад 7. Розв’язати нерівність

Розв’язання

Зрозуміло, що розв’язки цієї нерівності будуть комплексні числа, бо

Введемо нев’язку маємо:

Тоді загальний розв’язок даної нерівності можна записати так:

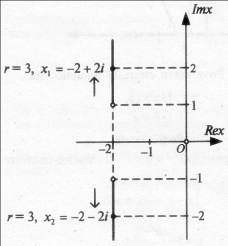
$E:\математика\Originals\img039.jpg$

На малюнку показано, що для конкретного значення (наприклад ) будемо мати два розв’язки:

Зрозуміло, що із збільшенням точка буде рухатися вгору, а – вниз. Отже, дана нерівність має комплексні розв’язки, геометрично зображені об’єднанням двох півосей, паралельних осі

Появу комплексних розв’язків можна спостерігати й у випадку неповних квадратних нерівностей.

Зображати графік залежності набагато складніше через появу додаткової осі , тобто треба будувати залежність не на площині, а в просторі, інакше губляться комплексні значення . Тому обмежимося побудовою комплексних розв’язків.

Приклад 8. Розв’язати нерівність

Розв’язання

Введемо параметр , маємо рівняння:

звідки

Залежно від знака підкореневого виразу маємо два випадки:

1). Тоді

Якщо то

Якщо то .

Отже,

2). Тоді тобто

Отже,

Тоді загальний розв’язок нерівності запишеться так:

Отже, нерівність має, крім дійсних, ще й комплексні розв’язки, виявити які легко методом нев’язки. Зокрема, якщо то отримаємо розв’язки

Якщо то отримаємо розв’язки:

$E:\математика\Originals\Originals\img039.jpg$

Приклад 9. Розв’язати нерівність

Розв’язання

Вводимо параметр , маємо рівняння:

звідки

Залежно від знака підкореневого виразу маємо два випадки:

1). Тоді

Якщо

Отже,

2). Тоді тобто

Отже,

Тоді загальний розв’язок нерівності запишеться так:

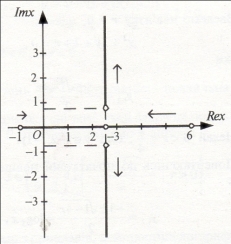
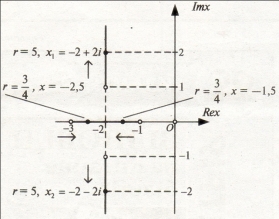
$E:\математика\img041.jpg$

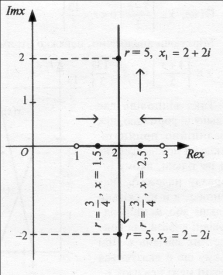
Як бачимо з малюнка, для вибраних значень нев’язки матимемо такі розв’язки:

Перевірку знайдених розв’язків пропонуємо виконати самостійно.

Ірраціональні нерівності

Приклад 10. Розв’язати нерівність

Розв’язання

Дана нерівність зводиться до системи нерівностей:

Кожну нерівність системи розв’яжемо методом нев’язки.

Введемо параметр

1).

звідки

Якщо

Тобто

2).

звідки

Тому

3).

звідки

Залежно від матимемо два випадки.

Якщо , то підкореневий вираз додатний. Отже, існують дійсні розв’язки.

Якщо , то підкореневий вираз від’ємний, а тому маємо комплексні розв’язки:

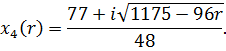
Якщо , то маємо:

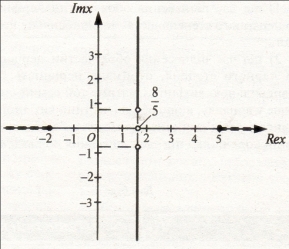
$E:\математика\Originals\img041.jpg$

Як бачимо з малюнка, крім дійсних розв’язків, з’являються ще й комплексні.

Виконаємо перевірку того, чи задовольняють знайдені комплексні розв’язки дану нерівність. Підставимо у нерівність значення

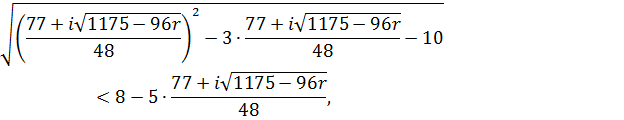
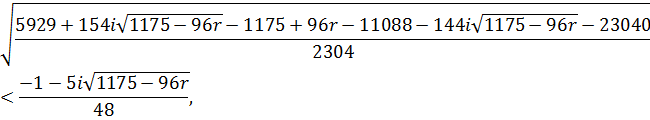
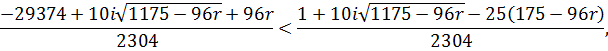
звідки

Оскільки , то маємо правильну нерівність.

Отже, комплексні розв’язки задовольняють дану нерівність. Тому

Розв’язками ірраціональних нерівностей можуть бути й комплексні числа, отримати які можна, використовуючи метод нев’язки. Зрозуміло, що їх поява пов’язана з функціями, які містить ірраціональна нерівність, або зі степенем кореня (радикала). Тому розв’язуючи ірраціональну нерівність, пропонуємо спочатку перейти до системи алгебраїчних нерівностей і зводити кожну з нерівностей системи до рівнянь.

Розв’язуючи ірраціональні нерівності, треба пам’ятати, що:

1). Під час піднесення обох частин нерівності до непарного степеня дістаємо рівносильну нерівність;

2). Під час піднесення обох частин нерівності до парного степеня, отримана нерівність буде рівносильною вихідній і матиме той самий смисл лише у випадку, якщо обидві частини вихідної нерівності невід’ємні; інакше можуть з’явитися сторонні корені (як і під час піднесення до квадрата).

Показникові нерівності

Приклад 11. Розв’язати нерівність

Розв’язання

Оскільки , то

Введемо нев’язку , маємо:

звідки

Залежно від значення , матимемо два випадки:

1).

Якщо

Якщо то

2).

Тоді матимемо комплексні розв’язки

$E:\математика\img042.jpg$

Перевіримо, чи задовольняють комплексні розв’язки дану нерівність. Підставимо у нерівність значення , маємо:

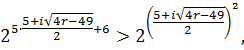
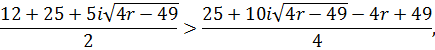
Якщо , то матимемо правильну нерівність. Отже, комплексні розв’язки задовольняють дану нерівність. Тому

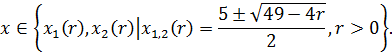
Логарифмічні нерівності

Приклад 12. Розв’язати нерівність

Розв’язання

Введемо нев’язку , маємо:

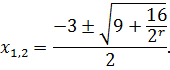
Якщо

Отже,

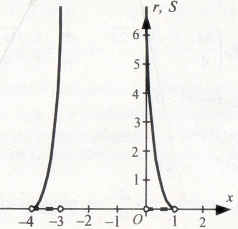
Розв’яжемо дану нерівність інакше. Нерівність рівносильна системі

Розв’яжемо кожну нерівність окремо, використовуючи метод нев’язки.

1).

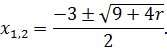
Якщо

Отже,

2).

Нехай

Якщо

Отже,

Нехай Маємо комплексні розв’язки логарифмічної нерівності:

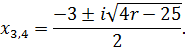
Перевіримо, чи задовольняють вони дану нерівність. Підставимо у нерівність значення

Маємо:

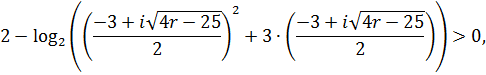
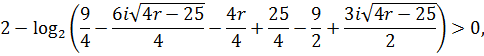
Для значень ця рівність справджується. Отже, комплексні розв’язки задовольняють дану нерівність.

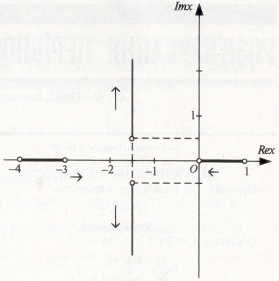
Розв’язок запишемо у вигляді

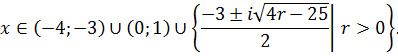
Цікаво, що в першому випадку розв’язки знайти не вдалося. Тому під час розв’язування логарифмічних нерівностей, які містять квадратичні функції, бажано спочатку використати загальноприйнятий спосіб розв’язування, отримати систему нерівностей, які вже й розв’язувати методом зведення до рівнянь.

Приклад 13. Розв’язати нерівність

Розв’язання

Позначивши , дістанемо :

Введемо нев’язку , маємо:

звідки

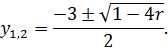
Нехай , тоді

Повертаючись до початкової невідомої , маємо:

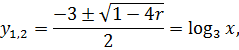
Якщо

Отже,

Нехай Тоді отримаємо комплексні розв’язки

Повертаючись до початкової невідомої , маємо:

Перевіримо, чи задовольняють комплексні розв’язки дану нерівність.

Підставимо у нерівність значення

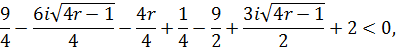
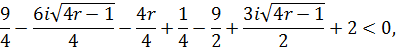
Для значень ця нерівність правильна.

Отже, комплексні розв’язки задовольняють дану нерівність. Розв’язок запишемо у вигляді

Як бачимо з прикладів, найпростіші логарифмічні нерівності краще розв’язувати, безпосередньо зводячи їх до рівнянь, а складніші краще спочатку звести до відповідної системи алгебраїчних нерівностей, а вже потім кожну нерівність системи звести до рівнянь.

Тригонометричні нерівності

Приклад 14. Розв’язати нерівність

Розв’язання

Введемо нев’язку і замінимо нерівність системою

Маємо два випадки.

1). Для дійсних розв’язків

або, з урахуванням того, що , маємо:

Розв’язки запишемо у вигляді

Якщо то

2). Для комплексних розв’язків

З урахуванням того, що маємо:

Тоді розв’язки можна записати у вигляді:

Отже, множина розв’язків, яка складається з пар чисел , у кожному із зчисленної множини інтервалів структурована і в загальному випадку розв’язки нерівності можна записати так:

Аналогічно можна отримати формули для розв’язування інших нерівностей даного типу.

Приклад 15. Розв’язати нерівність

Розв’язання

Введемо нев’язку і замінимо дану в умові нерівність системою

1). Для дійсних розв’язків

або, з урахуванням того, що , маємо:

Розв’язки запишемо у вигляді

Якщо , то

2). Для комплексних розв’язків

З урахуванням того, що маємо:

Тоді розв’язки можна записати у вигляді:

Приклад 16. Розвязати нерівність

Розв’язання

Введемо нев’язку маємо:

Якщо то

Приклад 17. Розв’язати нерівність

Розв’язання

Введемо нев’язку , маємо:

Якщо , то

Якщо то

ВИСНОВКИ

У сучасних умовах розвитку суспільства досягти життєвого успіху може лише творча особистість, з особливим стилем критичного мислення. Саме робота над цією науково-дослідницькою роботою створила мені умови для самореалізації.

Китайська мудрість проголошує: «…Покажи мені – і я запам’ятаю. Дай мені діяти самому – і я навчуся…». Для мене уміння працювати самостійно є дуже важливим й у житті. Дуже часто показником успіху є не тільки кінцевий результат, а й процес його досягнення.

Під час написання роботи, я збільшила свої знання, і вдосконалила вміння. Мої дослдіження привели мене до досягнення певного результату. Всі нерівності, які я розглядала у своїй роботі можна розв’язувати стандартним добре вивченим методом, але я дослідила застосування способу нев’язки, який дозволяє запобігти помилкам певного роду. Множина розв’язків нерівності структурована: кожному r > 0 ставиться у відповідність єдиний розв’язок x(r), який задовольняє нерівність.

Я дослдіила, що розвязуючи логарифмічні нерівності не завжди вдасться знайти розв’язки звичайним методом, який спочатку використовується для отримання системи нерівностей, які в свою чергу розв’язуються методом зведення до рівнянь з урахуванням нев’язки.

Я не тільки ознайомилася з розвязуванням нерівностей, зведенням до рівнянь, з урахуванням нев’язки, а й підвищила рівень своїх розумових та пізнавальних здібностей; почала виробляти в собі здатність до аналізу, синтезу, узагальнення і конкретизації, вміння логічно мислити. Я збагатила свою математичну культуру. Формувала навички дослідницької діяльності.

«Щоб засвоїти знання, треба смакувати їх з апетитом». Ці слова французького письменника ХІХ ст.. Анатоля Франса, стали для мене творчим кредом при праці над цією роботою. Адже тільки праця з бажанням, дає позитивні результати.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

Алімов Ш.А. Алгебра і початки аналізу: Підр. для 10-11 кл. середовищ. шк. - М.:Просвітництво, 1993.
Башмаков М.І. Алгебра і початки аналізу: Підр. для 10-11 кл. середовищ. шк. - М.: Просвітництво, 1992.
Віленкін Н.Я. та ін Алгебра і математичний аналіз для 11 класу: Навч. посібник для учнів шк. і кл. з поглиблений. вивч. математики. - М.: Просвітництво, 1998.
Григор'єв А.М. Ірраціональні рівняння. / / Квант, № 1, 1972.
Колмогоров А.Н. Алгебра і початки аналізу.Підр. для 10-11 кл. середовищ. шк. - М.: Просвітництво, 1991.
Кузнєцова Г.М. Програма для загаль. шкіл, гімназій, ліцеїв: Математика.5-11 кл. - М.: Дрофа, 2004.
Резуненко В.О. Ярмак В.О. Тригонометричні рівняння і нерівності для старшокласників і абітурієнтів. - Х.:Вид.група "Основа" 2011.
Корнієнко Т.Л., Фіготіна В.І. Факультативи та курси за вибором. Алгебра 10 – 11 кл. Методи розвя’язування рівнянь, нерівностей та їх системи: Навч. посіб.
В.А.Ясінський Практикум з розв'язування задач математичних олімпіад. — X.: Вид. гр. «Основа», 2006.
Семенов В. О., Тристан В. М. Доведення нерівностей. Показникові і логарифмічні нерівності.Х.Вид.група «Основа», 2007.
О.М.Вороний Готуємось до олімпіади з математики. Книга 1. — X. : Вид. група «Основа», 2008.
О.М.Вороний Готуємось до олімпіади з математики. Книга 2. — X. : Вид. група «Основа», 2008.
Фурман М. С. Збірник задач з алгебри і початків аналiзу. 11 клас.— Х. : Вид. група «Основа», 2010.

doc

Завантажити

Зберегти на потім

Додав(-ла)

Кровіцька Лариса Ярославівна

Пов’язані теми

Математика, 11 клас, Матеріали до уроків

Додано

5 березня 2023

Переглядів

291

Оцінка розробки

Відгуки відсутні