Самостіна робота на тему: " Коло. Круг. Дотична до кола". (8 варіантів)

 Самостійна робота

 Варіант 1 

1.    3 точки кола проведено дві хорди, які дорівнюють його радіусу. Знай­діть кут між ними.

А) 30^°; Б) 60^°; В) 90^°; Г)120^°.

2. Діаметр кола з центром у точці О дорівнює 8 см. Знайдіть периметр трикутника АОС, якщо хорда АС дорівнює 5 см.

А) 8 см; Б) 9 см; В) 13 см; Г) 18 см.

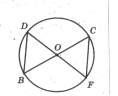
3.    На рисунку ВС і DF — діаметри кола з центром у точці О. Яке твердження неправильне:

А)   ∆ВОD — рівносторонній; Б) ∆ ВОD — рівнобедрений;

 В)  ∆ВОD = ∆COF; Г) Точка О – середина ВС.

 

Самостійна робота

 Варіант 2

1.    3 точки кола проведено діаметр і хорду, яка дорівнює його радіусу. Знайдіть кут між ними.

А) 30^°; Б) 60^°; В) 90^°; Г)120^°.

2.    Діаметр кола з центром у точці О дорівнює 10 см. Знайдіть периметр трикутника МОК, якщо хор­да МК дорівнює 8 см.

А) 8 см; Б) 9 см; В) 13 см; Г) 18 см.

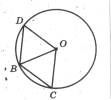
4.    На рисунку ВС і ВD — рівні хорди кола з цен­тром у точці О. Яке твердження неправильне:

А)      ∆ ВОD — рівнобедрений; Б)  ∆ ВОD — рівносторонній;

В)     ∆ ВОD = ∆ ВОС; Г) СО=ВО=DO.

 

 

 

Самостійна робота

 Варіант 3 

1.    Діаметр кола з центром у точці О дорівнює 8 см. Знайдіть периметр трикутника АОС, якщо хорда АС дорівнює 5 см.

А)  18 см; Б) 9 см; В) 8 см; Г) 13  см.

2.    3 точки кола проведено дві хорди, які дорівнюють його радіусу. Знай­діть кут між ними.

А) 30^°; Б) 60^°; В) 120^°;  Г) 90^°;

3.    На рисунку ВС і DF — діаметри кола з центром у точці О. Яке твердження неправильне:

А)   ∆ВОD = ∆COF; Б) ∆ ВОD — рівносторонній;

 В)  ∆ВОD — рівнобедрений; Г) Точка О – середина ВС.

 

Самостійна робота

 Варіант 4

1.    Діаметр кола з центром у точці О дорівнює 10 см. Знайдіть периметр трикутника МОК, якщо хор­да МК дорівнює 8 см.

А)  18 см; Б) 9 см; В) 13 см; Г) 8 см.

2.    3 точки кола проведено діаметр і хорду, яка дорівнює його радіусу. Знайдіть кут між ними.

А) 30^°; Б) 90^°; В) 60^°; Г)120^°.

3.    На рисунку ВС і ВD — рівні хорди кола з цен­тром у точці О. Яке твердження неправильне:

А)      ∆ ВОD — рівнобедрений; Б)  СО=ВО=DO;

В)     ∆ ВОD = ∆ ВОС; Г) ∆ ВОD — рівносторонній.

 

 

 

Самостійна робота

 Варіант 5 

1.    На рисунку ВС і DF — діаметри кола з центром у точці О. Яке твердження неправильне:

А)   ∆ВОD — рівносторонній; Б) ∆ ВОD — рівнобедрений;

 В)  ∆ВОD = ∆COF; Г) Точка О – середина ВС.

 

2.    3 точки кола проведено дві хорди, які дорівнюють його радіусу. Знай­діть кут між ними.

А) 120^°; Б) 60^°; В) 90^°; Г) 30^°.

3. Діаметр кола з центром у точці О дорівнює 8 см. Знайдіть периметр трикутника АОС, якщо хорда АС дорівнює 5 см.

А) 8 см; Б) 13 см; В) 9 см; Г) 18 см.

 

Самостійна робота

 Варіант 6

1.    На рисунку ВС і ВD — рівні хорди кола з цен­тром у точці О. Яке твердження неправильне:

А)      ∆ ВОD — рівносторонній; Б)  ∆ ВОD — рівнобедрений;

В)     ∆ ВОD = ∆ ВОС; Г) СО=ВО=DO.

 

2.    3 точки кола проведено діаметр і хорду, яка дорівнює його радіусу. Знайдіть кут між ними.

А) 60^°; Б) 30^°; В) 90^°; Г)120^°.

3.    Діаметр кола з центром у точці О дорівнює 10 см. Знайдіть периметр трикутника МОК, якщо хор­да МК дорівнює 8 см.

А) 8 см; Б) 18 см; В) 13 см; Г) 9 см.

 

Самостійна робота

 Варіант 7 

1.    На рисунку ВС і DF — діаметри кола з центром у точці О. Яке твердження неправильне:

А)   Точка О – середина ВС; Б)∆ ВОD — рівнобедрений;

 В)  ∆ВОD = ∆COF; Г) ∆ВОD — рівносторонній.

 

2. Діаметр кола з центром у точці О дорівнює 8 см. Знайдіть периметр трикутника АОС, якщо хорда АС дорівнює 5 см.

А) 8 см; Б) 18 см; В) 9 см; Г) 13 см.

3.    3 точки кола проведено дві хорди, які дорівнюють його радіусу. Знай­діть кут між ними.

А) 60^°; Б) 120^°; В) 90^°; Г) 30^°.

 

Самостійна робота

 Варіант 8

1.    На рисунку ВС і ВD — рівні хорди кола з цен­тром у точці О. Яке твердження неправильне:

А)      ∆ ВОD — рівносторонній; Б)  ∆ ВОD — рівнобедрений;

В)     ∆ ВОD = ∆ ВОС; Г) СО=ВО=DO.

 

2.    3 точки кола проведено діаметр і хорду, яка дорівнює його радіусу. Знайдіть кут між ними.

А) 90^°; Б) 30^°; В) 60^°; Г)120^°.

3.    Діаметр кола з центром у точці О дорівнює 10 см. Знайдіть периметр трикутника МОК, якщо хор­да МК дорівнює 8 см.

А) 8 см; Б) 18 см; В) 13 см; Г) 9 см.