Самостійна робота "Координати у просторі"
Самостійна робота з теми: «Координати в просторі»
В – 1
1 частина
- Яка з точок належить площині ОХУ:
А) (3; 0; – 4); Б) (0; 3; – 4); В) (3; – 4; 0); Г) (0; 0; 3)
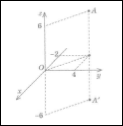
- Визначить координати точки А в просторі:
А) (4; 6;– 2); Б) (–2; 4; 6); В) (6;– 2; 4) Г) (–2; 6; 4)
- Найти відстань від точки А до площини ОХZ:
А) 2; Б) 4; В) 6; Г) інша відповідь
- Указати рівняння сфери с центром в точці (0; – 1; 0), що дотикається до площини у = 2:
А) х2 + (у + 1)2 + z2 = 4; Б) х2 + (у + 1)2 + z2 = 9;
В) х2 + (у – 1)2 + z2 = 9; Г) х2 + (у – 1)2 + z2 = 3;
2 частина
- Побудувати точки: А(6; 0; 0), В(0; 0; 5), С(0; 3; – 2), Е(2; 4; 3).
- Знайти довжину медіани ВМ трикутника АВС, якщо А(–2; 3; 5), В(1; – 3; 5); С(4; –3; 1).
- Найти відстань від точки А(3; 4; –3) до осі ОZ.
- Скласти рівняння сфери з центром в точці А(1; –1; 2), що проходить через точку М(–2; 0; 1)
3 частина
- Найти радіус і координати центра сфери, що задана рівнянням: х2 + у2 + z2 – 2x + 4y – 2z = 31.
------------------------------------------------------------------------------------
Самостійна робота з теми: «Координати в просторі»
В – 2
1 частина
- Яка з точок належить площині ОУZ:
А) (3; 0; – 4); Б) (0; 3; – 4); В) (3; – 4; 0); Г) (0; 0; 3)
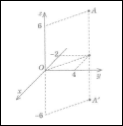
2. Визначить координати точки А! в просторі:
А) (4; –6;– 2); Б) (–2; 4; –6);
В) (–6;– 2; 4) Г) (–2; –6; 4)
- Знайти відстань від точки А до площини ОХY:
А) 2; Б) 4; В) 6; Г) інша відповідь
- Указати рівняння сфери с центром в точці (0; – 1; 0), що дотикається до площини у = 1:
А) х2 + (у + 1)2 + z2 = 4; Б) х2 + (у + 1)2 + z2 = 9;
В) х2 + (у – 1)2 + z2 = 4; Г) х2 + (у – 1)2 + z2 = 3;
2 частина
- Побудувати точки: А(0; 4; 0), В(0; 0; 2), С(0; –2; 3), Е(3; 2; 1).
- Знайти довжину медіани АМ трикутника АВС, якщо А(–2; 3; 5), В(1; – 3; 5); С(4; –3; 1).
- Найти відстань від точки А(3; 4; –3) до осі ОX.
- Скласти рівняння сфери з центром в точці М(1; 1; 3), що проходить через точку А(2; 0; – 1)
- частина
- Найти радіус і координати центра сфери, що задана рівнянням: х2 + у2 + z2 + 6x – 2y = 26.
--------------------------------------------------------------------------------------------


про публікацію авторської розробки
Додати розробку
