Самостійна робота "Вектори у просторі"
Самостійна робота.
Тема: «Вектори в просторі»
В – 1
-
Відомо, що А(1; 0), В(0; 1), О(0; 0). Знайдіть координати вектора, що дорівнює
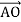 +
+ 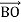 :
:
А) ( 1; 1); Б) (1; 0); В) (1; – 1); Г) (– 1; 1) Д) (0; 1)
-
Вектори
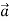 (2 – х; у +3; z – 5) та
(2 – х; у +3; z – 5) та 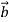 (5; 0; – 1) такі, що
(5; 0; – 1) такі, що 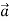 =
= 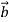 .
.
Знайдіть х + у + z.
- – 6; Б) 4; В) – 2; Г) 10; Д) – 4.
-
Обчисліть значення n, при якому вектори
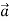 (n; 3) і
(n; 3) і 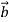 (2; – 1) колінеарні.
(2; – 1) колінеарні.
А) – 1,5; Б) 3; В) 6; Г) – 6; Д) 1.
-
Знайдіть координати вектора
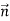 =
= 
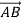 +
+ 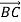 , якщо В(–1;2; 3), С(0; – 1; – 2), А(– 3; – 2; – 1).
, якщо В(–1;2; 3), С(0; – 1; – 2), А(– 3; – 2; – 1).
А) (![]() ); Б) (
); Б) (![]() ) ; В) (
) ; В) (![]() ); Г) (
); Г) (![]() )
)
-
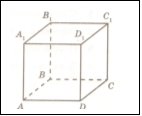 Дано куб АВСДА1В1С1Д1. Нехай
Дано куб АВСДА1В1С1Д1. Нехай
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() . Який із наведених векторів дорівнює вектору
. Який із наведених векторів дорівнює вектору ![]() –
– ![]() –
– ![]() ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ;
;
Г) ![]() ; Д)
; Д) ![]()
-
Знайдіть скалярний добуток векторів
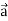 (– 1; 3;– 2) і
(– 1; 3;– 2) і 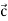 (0; –1; 5)
(0; –1; 5)
А) – 14; Б) – 13; В) 0; Г) 7; Д) 4.
- Установіть відповідність між векторами (1-4) і їх довжинами (А-Д)
1). ![]() (–1; 1; 0) А) 0
(–1; 1; 0) А) 0
2). ![]() , А(
, А(![]() ; 0; 1) , В(
; 0; 1) , В(![]() ; 1; 0) Б) 1
; 1; 0) Б) 1
3). ![]() (3; 0; 4) В)
(3; 0; 4) В) ![]()
4). ![]() , С(0; 5) Г) 2;
, С(0; 5) Г) 2;
Д) 5.
- Установіть відповідність між векторами, зображеними на рисунках (1-4) та їхніми скалярними добутками (А-Д)
|
вектор |
Скалярний добуток |
|
|
А) – 3 Б) – 2 В) 3; Г) 0 Д) 6 |
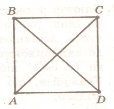
- На рисунку зображено квадрат АВСД. Установіть відповідність між кутами (1-4) та градусними мірами цих кутів (А-Д)
|
1) кут між векторами
2) кут між векторами
3) кут між векторами
4) кут між векторами |
А) 0о Б) 45о В) 90о Г) 135о Д) 180о |
|
-
У прямокутному трикутнику АВС катети АС і ВС відповідно дорівнюють 5 та 9. Знайдіть скалярний добуток векторів
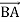 та
та 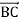 .
.
Самостійна робота.
Тема: «Вектори в просторі»
В – 2
-
Відомо, що А(1; 0), В(0; 1), О(0; 0). Знайдіть координати вектора, що дорівнює
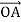 +
+ 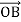 :
:
А) ( 1; 1); Б) (1; 0); В) (1; – 1); Г) (– 1; 1) Д) (0; 1)
-
Вектори
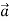 (х – 2; у + 1; 5 – z) та
(х – 2; у + 1; 5 – z) та 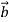 (1; 0; –2) такі, що
(1; 0; –2) такі, що 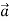 =
= 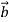 .
.
Знайдіть х + у + z.
- – 5; Б) 11; В) – 9; Г) 9; Д) 5.
-
Обчисліть значення у, при якому вектори
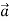 (5; – 4) і
(5; – 4) і 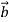 (1; у) колінеарні.
(1; у) колінеарні.
А) – 0,8; Б) 1,25; В) 0,8; Г) – 1,25; Д) 0,6.
-
Знайдіть координати вектора
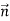 =
= 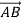 +2
+2 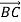 , якщо В(–1;2; 3), С(0; – 1; – 2), А(– 3; – 2; – 1).
, якщо В(–1;2; 3), С(0; – 1; – 2), А(– 3; – 2; – 1).
А) (![]() ); Б) (
); Б) (![]() ) ; В) (
) ; В) (![]() ); Г) (
); Г) (![]() )
)
-
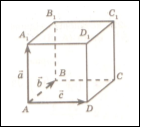 Дано куб АВСДА1В1С1Д1.
Дано куб АВСДА1В1С1Д1.
За рисунком виразіть вектор ![]() через вектори
через вектори ![]() ;
; ![]() ;
; ![]() ?
?
А)![]() +
+ ![]() –
– ![]() ; Б)– (
; Б)– ( ![]()
![]() +
+ ![]() );
);
В) ![]() +
+ ![]() +
+ ![]() ; Г) –
; Г) –![]() –
– ![]() ; Д)
; Д) ![]() +
+ ![]() .
.
-
Знайдіть скалярний добуток векторів
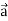 (– 1; – 3; 2) і
(– 1; – 3; 2) і 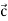 (1; 0; 5)
(1; 0; 5)
А) 11; Б) 6; В) 9; Г) – 9; Д) – 1.
- Установіть відповідність між векторами (1-4) і їх довжинами (А-Д)
1). ![]() (–1; 1; 0) А) 1
(–1; 1; 0) А) 1
2). ![]() , А(
, А(![]() ; 0; 1) , В(
; 0; 1) , В(![]() ; 1; 0) Б) 2
; 1; 0) Б) 2
3). ![]() (3; 0; 4) В)
(3; 0; 4) В) ![]()
4). ![]() , С(0; 5) Г) 0;
, С(0; 5) Г) 0;
Д) 5.
- Установіть відповідність між векторами, зображеними на рисунках (1-4) та їхніми скалярними добутками (А-Д)
|
вектор |
Скалярний добуток |
|
|
А) – 2 Б) – 3 В) 6; Г) 3 Д) 0 |
- На рисунку зображено квадрат АВСД. Установіть відповідність між кутами (1-4) та градусними мірами цих кутів (А-Д)
|
1) кут між векторами
2) кут між векторами
3) кут між векторами
4) кут між векторами |
А) 90о Б) 135о В) 180о Г) 45о Д) 0о |
|
-
Знайдіть скалярний добуток векторів
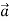 +
+ 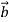 і
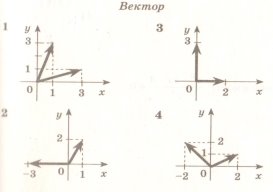
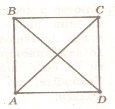
і 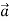 –
– 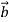 , якщо
, якщо
![]() (3; 2),
(3; 2), ![]() (2; – 1).
(2; – 1).


про публікацію авторської розробки
Додати розробку

-

Перевертень Світлана Михайлівна
25.01.2022 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Аліна Білогуб
14.04.2021 в 22:17
Відповідей не завадалоб
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Oksana
17.04.2020 в 15:02
Хотілося б відповідей. Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Патик Лідія Іванівна
10.03.2020 в 07:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук