Самостійна робота "Лінійні нерівності. Числові проміжки"
Про матеріал
Самостійна робота дозволить перевірити компетентності учнів розв'язувати лінійні нерівності. Робота містить 4 однакових за складністю варіанти. Перегляд файлу
САМОСТІЙНА РОБОТА
ВАРІАНТ І
-
Який з проміжків є розв'язком нерівності
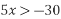 .
.
- Розв’яжіть лінійну нерівність:
- Зобразіть проміжки на координатній прямій та запишіть їх переріз:
-
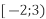 і
і 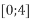
-
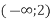 і
і 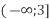
-
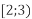 і
і 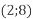
- Зобразіть проміжки на координатній прямій та запишіть їх об’єднання:
-
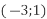 і
і 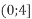
-
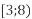 і
і 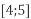
-
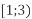 і
і 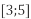
САМОСТІЙНА РОБОТА
ВАРІАНТ ІІ
-
Який з проміжків є розв'язком нерівності
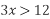 .
.
- Розв’яжіть лінійну нерівність:
- Зобразіть проміжки на координатній прямій та запишіть їх переріз:
-
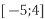 і
і 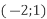
-
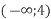 і
і 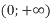
-
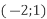 і
і 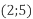
- Зобразіть проміжки на координатній прямій та запишіть їх об’єднання:
-
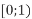 і
і 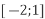
-
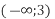 і
і 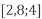
-
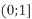 і
і 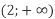
САМОСТІЙНА РОБОТА
ВАРІАНТ ІII
-
Який з проміжків є розв'язком нерівності
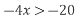 .
.
- Розв’яжіть лінійну нерівність:
- Зобразіть проміжки на координатній прямій та запишіть їх переріз:
-
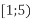 і
і 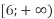
-
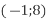 і
і 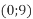
-
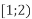 і
і 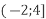
- Зобразіть проміжки на координатній прямій та запишіть їх об’єднання:
-
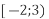 і
і 
-
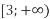 і
і 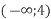
-
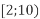 і
і 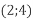
САМОСТІЙНА РОБОТА
ВАРІАНТ ІV
-
Який з проміжків є розв'язком нерівності
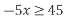 .
.
- Розв’яжіть лінійну нерівність:
- Зобразіть проміжки на координатній прямій та запишіть їх переріз:
-
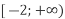 і
і 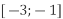
-
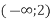 і
і 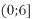
-
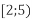 і
і 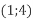
- Зобразіть проміжки на координатній прямій та запишіть їх об’єднання:
-
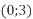 і
і 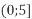
-
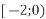 і
і 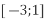
-
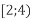 і
і 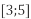
docx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
