Урок-гра "Аксіоми стереометрії та їх найпростіші наслідки, паралельність прямих і площин, перпендикулярність прямих та площин

Тема уроку: Аксіоми стереометрії та їх найпростіші наслідки, паралельність прямих і площин, перпендикулярність прямих і площин.

Мета уроку: повторити навчальний матеріалів з названих тем, розвивати навички використання теоретичних знань до розв’язування задач, пізнавальну активність учнів, культуру спілкування, вміння формулювати відповіді на запитання.

Обладнання: таблиці, роздатковий матеріал.

Тип уроку: урок узагальнення і систематизації знань, умінь і навичок.

ХІД УРОКУ

І. Організаційний момент

Урок проводиться у вигляді гри «Щасливий випадок». Гра складається з чотирьох геймів, результати яких оцінюються журі. У грі беруть участь дві команди 10-го класу.

ІІ. Гра.

І гем «Далі, далі, далі…»

Кожній команді пропонується по 15 запитань. Час відповіді на всі запитання команди – 3 хвилини. Відповідають члени команди по черзі, яку визначає капітан  команди. Кожна правильна відповідь оцінюється 1 балом. Якщо учень не може відповісти, то він говорить «Далі…», при цьому команда втрачає один бал. Відповісти на це запитання може наступний учень, але за правильну відповідь йому зараховується 0,5 бала. Після цього він відповідає на своє запитання.

Запитання першій команді

1. Сформулюйте аксіому стереометрії С₁.

(Яка ба не була площина, існують точки,

що належать цій площині, і точки, які не належать їй.)

2. Чи можна стверджувати, що будь-які дві точки завжди лежать на одній прямій: так чи ні?

(Так.)

3. Дві прямі в просторі називаються паралельними, якщо …

(вони лежать в одній площині і не перетинаються)

4. Чи можуть дві різні площини мати лише одну спільну точку?

(Ні.)

5. Якщо прямі АВ і СD мимобіжні, то прямі АС і ВD…

(мимобіжні.)

6. Пряма а паралельна площині . Чи існують у площині прямі, не паралельні прямій а?

(так.)

7. Чи можуть бути паралельними площини, які проходять через не паралельні прямі?

(Так.)

8. Якщо дві площини паралельні третій, то…

(вони паралельні між собою.)

9. Відрізки паралельних прямих, які знаходяться між двома паралельними площинами, …

(рівні.)

10. Чи можна при паралельному проектуванні прямокутника отримати трапецію?

(Ні.)

11. Пряма називається перпендикулярною до площини, …

(якщо вона перпендикулярна до будь-якої прямої,

що лежать у цій площині й проходить через точку площини.)

12.          Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна до жодної прямої цієї площини?

(Ні.)

13.          Через одну зі сторін трикутника можна провести площину , перпендикулярну до другої сторони. Який це трикутник?

(Прямокутний.)

14.          Площина перпендикулярна до прямої b, а пряма b паралельна прямій с. яке взаємне розміщення площини і прямої с?

15.          Пряма а перпендикулярна до площини , а площина паралельна прямій с. Яке взаємне розташування прямих а і с?

(а і с мимобіжні.)

Запитання другій команді

1.     Сформулюйте аксіому стереометрії С₂.

(Якщо дві різні площини мають спільну точку,

то вони перетинаються по прямій, що проходить через цю точку.)

2.     Чи можна стверджувати, що будь-які чотири точки завжди лежать в одній площині?

(Ні.)

3.     Пряма і площина називаються паралельними, якщо…

(вони не перетинаються.)

4.     Чи правильно, що пряма, яка має з колом тільки одну спільну точку, є дотичною до кола в цій точці у просторі?

(Не можна стверджувати.)

5.     Прямі, що не перетинаються і не лежать в одній площині, називаються…

(мимобіжними.)

6.     Пряма а паралельна прямій b, а пряма b паралельна площині . Чи обов’язково пряма а паралельна площині

(Так.)

7.     Дві прямі паралельні третій,…

(якщо вони паралельні між собою.)

8.     Якщо площина перетинає одну з двох паралельних прямих, то вона…

(перетинає й другу.)

9.     Якщо дві паралельні площини перетинаються третьою площиною, то прямі перетину…

(паралельні.)

10. Чи можна при паралельному проектуванні прямокутника отримати паралелограм?

(Так.)

11. Дві прямі в просторі називаються перпендикулярними, якщо…

(вони перетинаються під прямим кутом.)

12. Скільки різних площин визначають прямі МА, МВ, МС?

(Три.)

13. Скільки прямих перпендикулярних до даної площини, можна провести через точку поза даною площиною?

(Одну.)

14. Площина перпендикулярна до прямої b, а пряма b перпендикулярна до прямої с. Яке взаємне розміщення площини і прямої с?

(с  )

15. Дві мимобіжні прямі мають спільний перпендикуляр і до того є …

(тільки один.)

ІІ гейм «Заморочки з бочки»

Кожному члену команди пропонується розв’язати по одній задачі. Учні вибирають задачу, із запропонованого конверта. За правильне розв’язання нараховується по одному або два бали залежно від рівня складності задачі.

Задачі з конвертів

1. Чи можна стверджувати, що через пряму і дві точки поза нею можна провести площину? (1 бал)
2. З точки до площини проведені перпендикуляр довжиною 5 см і похила довжиною 13 см. Знайти довжину проекції цієї прямої на площину. (1 бал)
3. З центра О правильного трикутника АВС зі стороною 9 см проведено перпендикуляр ОМ до його площини довжиною 3 см. Знайти кут МАО. (2 бали)
4. З вершини прямого кута С трикутника АВС до його площини проведено перпендикуляр СМ довжиною 4 см. Знайти відстань від точки М до АВ, якщо АС=ВС=8 см. (2 бали)
5. АВCDA1B1C1D1 – куб, довжина ребра якого дорівнює 4 см. Знайти відстань між прямими АС1 і ВВ1.

Геомузик

(між ІІ і ІІІ геймами пропонується музична пауза)

  Пропонуємо дати геометричну інтерпретацію фрагментам шести музичних творів. За  кожну правильну (чи можливу) інтерпретацію нараховується 1 бал.

1. «Місячна дорога» (слова М. Бакая; пряма на площині)

Місячна дорога край села

У холодних росах пролягла,
Повела з тобою нас в рідний край.

Не забудем ми дорогу ту,

І кохання нашого весну,

Не забудем,не забудем ми.

2. «Как провожают пароходи» (К. Ваншенкин; паралельні прямі)

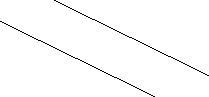Как провожают пароходи,

Сов сем не так как поезда.

Морские  медленние води

Не то, что рельси в два ряда.

3.  З кінофільму «Земля Санникова»  (перетин прямої з площиною)

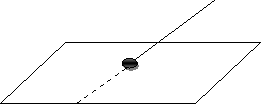Призрачно все в этом мире бушующем,

Есть только миг, за него и держись.

Есть только миг между прошлым и будущим,

Именно он називается жизнь.

4. «Повернення додому» (слова А. Кичинського, пряма, перпендикулярна до площини)

На відстані сльози

Над полум’ям рудим

Стоїть холодний дим

До самого неба

Холодний і гіркий

Іде в небо дим,

Теплішого мені, солодшого не треба.

5. «Журавлині ключі» (слова П. Лехновського; паралельні площини)

Журавлині ключі –

То чужі і незвідані далі,

Журавлині ключі –

Біль розлуки, страждання, печалі.

Журавлині ключі –

Промінці нездійсненної мрії,

 Журавлині ключі –

Непогашені іскри надії.

6. «Как провожают пароходи» (К. Ваншенкин; площина)

Как не шути – волнений больше,

Ведь ты уже не не земле.

Как не ряди – разлука дальше,

Когда плывеш на корабле.

Вода, вода, кругом вода.

Вода, вода, шумит вода.

ІІІ гейм «Темна конячка»

 Цей гейм проводить гість гри. Він пропонує учням такі завдання: у форматі задач і за посиланням https://learningapps.org/display?v=phg9s4f3k19.

Завдання І команді

1. У класній кімнаті показати перпендикулярні прямі.
2. Чи може бути пряма бути паралельною одночасно двом різним площинам? Проілюструвати на елементах класної кімнати.
3. Трикутник АВС є паралельною проекцією рівностороннього трикутника. Побудувати зображення перпендикулярів, проведених з точок М і N до сторін АС і АВ трикутника.

Завдання ІІ команді

1. У класні й кімнаті показати мимобіжні прямі.
2. Чи може пряма бути перпендикулярною одночасно до двох різних площин? Проілюструвати на елементах класної кімнати.
3. На зображенні паралельної проекції рівнобічної трапеції побудувати зображення її висот,проведених з вершин тупих кутів.

ІV гейм «Ти –  мені, я – тобі»

 Команди пропонують одна одній по одній задачі, яку вони підготували до уроку.

Задача І команди

 Кінці відрізка лежать у двох взаємно перпендикулярних площинах. Проекції відрізка на площини дорівнюють 20 см і 16 см. Відстань між основами перпендикулярів, проведених з кінців відрізка до лінії перетину площин, дорівнює 12 см. Знайти довжину відрізка.

Задача ІІ команди

 Кінці відрізка, довжина якого дорівнює 13 см, належать двом взаємно перпендикулярним площинам, а відстані від кінців відрізка до лінії перетину площин дорівнює 8 см і 5 см. Знайти відстань між основами перпендикулярів, проведених з кінців відрізка до лінії перетину площини.

ІІІ. Підсумок гри.

Оголошується команда-переможниця, учні які набрали більше балів.