Самостійна робота з теми: «Застосування похідної до дослідження функцій»

1. Розробити систему вправ для самостійної роботи учнів з теми:

«Застосування похідної до дослідження функцій»

Самостійна робота з теми: «Застосування похідної до дослідження функцій»  Початковий рівень

1.      Обчислити похідні:

-   Знайти похідну функції  f(x) = ;

-   Знайти похідну функції  f;

-   Знайти похідну функції  f(x) = .

2.      Знайти критичні точки функції  f(x) =   

Середній рівень:

3.      Дослідити на монотонність проміжки зростання та спадання функцію f(x) =  .

4.      Знайти точки екстремуму функції f(x) =  та визначте їхній характер (максимум чи мінімум).

Достатній рівень:

5.      Дослідження функції з використанням похідних другого порядку: дослідити на опуклість і вгнутість та знайдіть точки перегину функції  f(x) =    

6.      Знайти екстремуми та точки перегину функції  f(x) =  Високий рівень:

7.      Дослідити функцію f(x) на проміжки зростання та спадання,

знайдіть екстремуми, точки перегину, а також дослідіть на асимптоти.

8.      Знайти значення параметра а, при яких функція f(x) =  - 3ax + 2  має дві різні точки екстремуму.

Додаткові задачі для самостійного вирішення:

9.      Знайти максимальну площу прямокутника, вписаного в півколо радіусом 5 одиниць.

10.Знайти швидкість зміни об'єму кулі, якщо її радіус змінюється зі швидкістю 0.5 см/сек.

2.        Розробити систему вправ для самостійної роботи учнів з теми:

„Властивості первісної. Правила знаходження первісних”.

Самостійна робота з теми: «Властивості первісної. Правила знаходження первісних» Початковий рівень:

1.               Знайдіть загальний вигляд первісної для наступних функцій:

1)    f(x) =;

2)    f(x) = cos x; 3)f(x) = ; 4) f(x) = .

2.               Перевірити, чи є функція F (x) = первісною для f(x) =.

Поясніть свій результат.

3.               Знайдіть константу С так, щоб первісна F (x) =  задовольняла умову F(1) = 5.

Середній рівень:

4.               Знайдіть первісну для функції, використовуючи правило лінійності:

1)    f(x) =;

2)    f(x) = 4 sin (x)3 cos (x);

5.               Використовуючи таблицю основних первісних, знайдіть первісну для функції: 

1)    f(x)= ;

2)    f(x)= ;

Достатній рівень:

6.               Знайдіть первісну для функції, яка є сумою двох функцій:

1)    f(x)=;

2)    f(x)=;

7.               Знайдіть загальний вигляд первісної для функції f(x)=; Високий рівень:

8.               Знайдіть первісну для функції f(x)=.

 

Виконати          додатково інтерактивну     вправу: https://learningapps.org/view8010077  

 

 

3.        Опрацювати матеріал книги Виленкин Н.Я. Комбінаторика (с.9-12, 31-59), підготувати конспект. 

Тема уроку: «Елементи комбінаторики» Мета: Навчальна:

•   Ознайомити учнів з основними поняттями комбінаторики: факторіалом, перестановками, розміщеннями та комбінаціями.

•   Навчити учнів використовувати формули для обчислення кількості перестановок, розміщень та комбінацій.

•   Розвинути вміння учнів розв'язувати комбінаторні задачі.

Виховна:

•   Виховувати в учнів інтерес до математики та прагнення до знань.

•   Розвивати в учнів логічне мислення, увагу, пам'ять та кмітливість.

•   Виховувати в учнів працьовитість, наполегливість та впевненість у власних силах.

Розвивальна:

•   Розвивати в учнів уміння аналізувати та систематизувати інформацію.

•   Розвивати в учнів математичну мову та культуру.

•   Розвивати в учнів творче мислення та вміння знаходити нестандартні рішення задач.

Хід уроку:

І. Організаційний момент: Доброго ранку, любі учні. Сьогодні ми будемо працювати над темою: «Елементи комбінаторики». Комбінаторика – це розділ математики, що вивчає задачі вибору, розташування та впорядкування елементів множин. Основні об'єкти дослідження включають перестановки, розміщення і комбінації. 

ІІ. Актуалізація опорних знань: Дану тему ми з вами розглядали в 9 класі, тому давайте оновимо наші знання за допомогою інтерактивної вправи з посиланням: https://learningapps.org/view4076445;

ІІІ. Вивчення нового матеріалу: 

Основні поняття комбінаторики

1.     Перестановки:

•   Перестановки без повторень: кількість способів розташування n елементів. Формула: 

•   Перестановки з повтореннями: кількість перестановок множини, де деякі елементи можуть повторюватися. Формула: 

2.     Розміщення:

•   Розміщення без повторень: кількість способів вибору та впорядкування k елементів з n без повторень. Формула: 

•   Розміщення з повтореннями: кількість способів вибору та впорядкування k елементів з n з повтореннями. Формула:  

3.     Комбінації:

•   Комбінації без повторень: кількість способів вибору k елементів з n без врахування порядку. Формула:  

•   Комбінації з повтореннями: кількість способів вибору k елементів з n

з врахуванням повторень. Формула:  

Додаткові методи

•   Рекурентні співвідношення: метод знаходження загальної формули через зв'язок з попередніми елементами.

•   Генеруючі функції: використовуються для вирішення задач, пов'язаних з рекурентними співвідношеннями та комбінаторними об'єктами.

Приклади задач

1.                        Задача про перестановки: Скільки різних способів можна розставити 5 книг на полиці?

2.                        Задача про розміщення: Скільки способів можна вибрати і впорядкувати 3 із 5 різних марок?

3.                        Задача про комбінації: Скількома способами можна вибрати 2 елементи з множини, що складається з 4 елементів?

IV. Розв’язання вправ та задач:

Вправа 1: Перестановки без повторень

Задача: Скільки існує різних способів розташувати 4 різні книги на полиці?

Розв'язок: Кількість перестановок n елементів обчислюється за формулою n!

Для 4 книг: =4!=4×3×2×1=24

Отже, існує 24 різні способи розташувати 4 книги.

Вправа 2: Перестановки з повтореннями

Задача: Скільки різних перестановок можна утворити зі слів "АНАНАС"?

Розв'язок: Кількість перестановок з повтореннями обчислюється за формулою Р =   

 

Для "АНАНАС": n =6, = 3, = 2,  = 1

P

Отже, існує 60 різних перестановок слова "АНАНАС".

Вправа 3: Розміщення без повторень

Задача: Скільки способів можна вибрати і впорядкувати 3 із 5 різних марок?

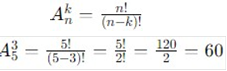Розв’язок: Кількість розміщень k елементів з n без повторень обчислюється за формулою: Для 3 з 5 марок: 

 

Отже, існує 60 способів вибрати і впорядкувати 3 із 5 різних марок.

Вправа 4: Комбінації без повторень

Задача: Скількома способами можна вибрати 2 елементи з множини, що складається з 5 елементів?

Розв'язок: Кількість комбінацій k елементів з n без повторень обчислюється за формулою  Для 2 з 5 елементів: 

 

Отже, існує 10 способів вибрати 2 елементи з 5.

Вправа 5: Комбінації з повтореннями

Задача: Скількома способами можна вибрати 3 елементи з множини з 4 елементів (з повторенням)?

Розв'язок: Кількість комбінацій k елементів з n з повтореннями обчислюється за формулою  Для 3 з 4 елементів: 

 

Отже, існує 20 способів вибрати 3 елементи з 4 з повторенням. V. Домашнє завдання: 

1)           Скільки різних перестановок можна скласти з літер слова "КНИГА"?

2)           Скількома способами можна розставити 3 червоні та 2 сині прапорці в ряд?

3)           Скількома способами можна вибрати 3 студента з групи з 10 студентів?

4)           На скільки способів можна розподілити 5 різних книг між трьома студентами, якщо кожен студент повинен отримати хоча б одну книгу?

VІ. Рефлексія:…

 

4.                    Опрацювати матеріал книги Кремер Н.Ш. Теорія вероятностей и

математическая статистика (с.16-35), підготувати конспект

Тема уроку: «Теорія ймовірностей та математичної статистики» Мета:  Навчальна:

•   Узагальнити та систематизувати знання учнів з основних понять теорії ймовірностей та математичної статистики.

•   Ознайомити учнів з новими поняттями та методами теорії ймовірностей та математичної статистики.

•   Навчити учнів застосовувати знання з теорії ймовірностей та математичної статистики для розв'язування задач та проблем.

Виховна:

•   Виховувати в учнів наукове світосприйняття, логічне мислення, прагнення до пізнання нового.

•   Розвивати в учнів самостійність, відповідальність, вміння працювати в команді.

•   Сприяти формуванню в учнів інтересу до математики та її застосування в різних галузях науки та техніки.

Розвивальна:

•   Розвивати в учнів пам'ять, увагу, уяву.

•   Вдосконалювати в учнів навички аналізу, синтезу, порівняння.

•   Формувати в учнів вміння досліджувати, робити висновки, узагальнення.

Хід уроку: 

I.         Організаційний момент: Вітаю, в нас сьогодні тема: «Теорія ймовірностей та математичної статистики». Сьогодні ми розпочинаємо вивчення нової теми - теорії ймовірностей та математичної статистики. Ці науки мають велике значення для сучасного життя. Вони використовуються в багатьох галузях науки та техніки, таких як економіка, фінанси, медицина, соціологія, інженерія та багато інших. Знання теорії ймовірностей та математичної статистики допоможуть вам краще розуміти світ навколо вас, приймати обґрунтовані рішення та робити точні прогнози.

II.      Перевірка домашнього завдання:

III.   Актуалізація опорних знань: Фронтальне опитування:

•               Що таке теорія ймовірностей?

•               Які основні поняття теорії ймовірностей?

•               Які методи математичної статистики ви знаєте?

•               Як теорія ймовірностей та математична статистика використовуються в реальному житті?

IV.  Вивчення нового матеріалу: 

1.1 Вступ до теорії ймовірностей

•   Визначення ймовірності: Ймовірність події - це числова міра ступеня впевненості в тому, що ця подія станеться.

•   Класична ймовірність:       Ймовірність         події A       визначається        як відношення числа сприятливих для неї результатів до загального числа можливих результатів у рівно ймовірному експерименті: 

1.2 Основні поняття і визначення

•   Випадкова подія: подія, результат якої не можна передбачити заздалегідь.

•   Простір елементарних подій: сукупність всіх можливих результатів експерименту.

•   Випадкова          величина: числова       характеристика    випадкового експерименту, що може набувати різних значень.

1.3 Операції над подіями

•   Об’єднання подій A∪B: подія, яка відбудеться, якщо відбудеться хоча б одна з подій A або B.

•   Перетин подій A∩B: подія, яка відбудеться, якщо відбудуться обидві події A та B.

•   Доповнення події  ̅: подія, яка відбудеться, якщо подія A не відбудеться.

1.4 Властивості ймовірності

•      Неможлива подія: подія, яка ніколи не відбудеться, має ймовірність 0.

•      Достовірна подія: подія, яка відбудеться завжди, має ймовірність 1.

•      Сума ймовірностей всіх можливих подій дорівнює 1.

1.5 Теореми ймовірності

•   Теорема додавання: Якщо події A та B несумісні, то ймовірність їх об’єднання P(A∪B)=P(A)+P(B).

•   Теорема множення: Якщо події A та B незалежні, то ймовірність їх перетину P(A∩B)=P(A)⋅P(B). Розділ 2: Основи математичної статистики

2.1 Вибіркові дослідження

•Вибірка: частина генеральної сукупності, яка використовується для оцінки параметрів цілої сукупності.

•Параметри вибірки: середнє, дисперсія, мода, медіана.

2.2 Основні поняття

•   Генеральна сукупність: повна сукупність усіх можливих об’єктів або результатів.

•   Вибіркова середня: середнє значення вибірки, яке використовується для оцінки середнього значення генеральної сукупності.

2.3 Оцінка параметрів

•   Точкові оцінки: конкретні числові значення, які є оцінками параметрів генеральної сукупності.

•   Інтервальні оцінки: інтервали, в яких з певною ймовірністю знаходяться параметри генеральної сукупності.

Розділ 3: Методи математичної статистики

3.1 Перевірка статистичних гіпотез

•   Гіпотеза: припущення щодо параметра генеральної сукупності, яке перевіряється на основі вибіркових даних.

•   Критичні значення: значення, які визначають область відхилення нульової гіпотези.

3.2 Регресійний аналіз

•Лінійна регресія: метод, що використовується для моделювання залежності між двома змінними.

•Коефіцієнт кореляції: міра лінійної залежності між двома змінними.

3.3 Дисперсійний аналіз

•   Однофакторний дисперсійний аналіз: метод, що використовується для визначення впливу одного фактора на змінну.

•   Двухфакторний дисперсійний аналіз: метод, що дозволяє оцінити вплив двох факторів та їх взаємодії на змінну.

V.     Розв’язання вправ та задач на засвоєння: 

Вправа 1.1: Класична ймовірність 

Завдання: Є урна, що містить 5 червоних і 3 синіх кульки. Знайдіть ймовірність витягнути червону кульку. 

Розв'язок: Ймовірність події A (витягнути червону кульку) визначається як відношення числа сприятливих результатів до загального числа можливих результатів.

 

Вправа 1.2: Теорема додавання ймовірностей 

Завдання: В ящику 7 білих, 3 чорні та 5 червоних кульок. Знайдіть ймовірність витягнути білу або чорну кульку. 

            Розв'язок:      Ймовірність     витягнути     білу     або     чорну      кульку:

 

Вправа 1.3: Теорема множення ймовірностей 

Завдання: У коробці є 4 сині та 6 зелених кульок. Витягуємо дві кульки послідовно без повернення. Знайдіть ймовірність, що обидві кульки будуть сині. 

Розв'язок: Ймовірність витягнути першу синю кульку: 

Ймовірність витягнути другу синю кульку після першої:  

Ймовірність обох подій: 

Розділ 2: Основи математичної статистики

Вправа 2.1: Вибіркова середня 

Завдання: Відомі наступні дані: 5, 7, 9, 10, 12. Знайдіть вибіркове середнє. 

Розв'язок: Вибіркове середнє обчислюється як сума всіх значень, поділена на їх кількість:  

 

Вправа 2.2: Вибіркова дисперсія 

Завдання: Для тих самих даних (5, 7, 9, 10, 12) обчисліть вибіркову дисперсію. 

            Розв'язок:      Вибіркова     дисперсія      обчислюється     за      формулою:

  

Спочатку обчислюємо відхилення кожного значення від середнього:

Додаємо ці значення: 12.96 + 2.56 + 0.16 + 1.96 + 11.56 = 29.2

Обчислюємо дисперсію: 

Розділ 3: Перевірка статистичних гіпотез

Вправа 3.1: Перевірка гіпотези про середнє значення 

Завдання: Гіпотеза: середній бал учнів класу дорівнює 75. Вибірка з 10 учнів має середній бал 72 і стандартне відхилення 5. Використовуйте рівень значущості 0.05 для перевірки гіпотези. 

Розв'язок: Використовуємо t-критерій:  

 

Критичне значення для df=9 і =0.05 становить приблизно 2.262. Оскільки

−1.9<2.262, немає підстав відкидати нульову гіпотезу.

 

VI.     Домашнє завдання:

Завдання 1.1: Класична ймовірність

В урні знаходиться 10 кульок: 4 червоні, 3 сині та 3 зелені. Знайдіть ймовірність витягнути синю кульку.

Завдання 1.2: Теорема додавання ймовірностей

У коробці 6 червоних, 8 синіх і 6 зелених кульок. Знайдіть ймовірність витягнути червону або зелену кульку. Розділ 2: Основи математичної статистики

Завдання 2.1: Вибіркова середня

Для даних 8, 12, 14, 10, 11 обчисліть вибіркове середнє.

Завдання 2.2: Оцінка параметрів

Для вибірки з 20 спостережень, середнє значення якої становить 15, а стандартне відхилення - 3, знайдіть 95%-ний довірчий інтервал для середнього значення генеральної сукупності.

Розділ 3: Перевірка статистичних гіпотез

Завдання 3.1: Перевірка гіпотези про середнє значення

Вибірка з 15 студентів показала середній бал 78 з стандартним відхиленням 4. Перевірте гіпотезу, що середній бал дорівнює 80, на рівні значущості 0.05.

VII.     Рефлексія…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Опрацювати матеріал книги Кремер Н.Ш. Теорія вероятностей и математическая статистика (с.264-275, 286-289), підготувати конспект

Тема уроку: «Елементи математичної статистики» Мета:  Навчальна:

•   Ознайомити учнів з основними поняттями математичної статистики: генеральна сукупність, вибірка, статистична частота, емпірична функція розподілу, ряди розподілу, статистичні міри центральної тенденції (середнє арифметичне, медіана, мода), статистичні міри розсіювання (вибіркове дисперсія, розмах, стандартне відхилення).

•   Навчити учнів обчислювати статистичні міри центральної тенденції та розсіювання для даних, представлених у вигляді таблиць та рядів розподілу.

•   Розвинути вміння учнів аналізувати та інтерпретувати статистичні дані. Виховна:

•   Виховувати в учнів наукову свідомість, прагнення до пізнання нового, самостійність та відповідальність за результати навчальної діяльності.

•   Сприяти розвитку логічного мислення, критичного ставлення до інформації, вміння працювати в команді.

Розвивальна:

•   Розвивати в учнів пізнавальні інтереси, математичні здібності, вміння використовувати математичні знання для розв'язання практичних задач.

•   Формувати в учнів інформаційну компетентність, навички роботи з комп'ютером.

Хід уроку:

I.         Організаційний момент: Вітаю, сьогодні розглядаємо тему «Елементи  математичної статистики». Математична статистика – це розділ математики, який займається методами збору, аналізу, інтерпретації та представлення даних. Вона є невід'ємною частиною досліджень у різних галузях знань, від економіки до біології, і відіграє важливу роль у прийнятті рішень на основі даних.

II.     Перевірка домашнього завдання… III.    Актуалізація опорних знань:

На іспиті з математики 10 учнів отримали оцінку "5", 8 учнів - "4", 4 учні - "3", 2 учні - "2". Складіть ряд розподілу та оберіть графічне зображення даних, яке найкраще його ілюструє.

IV.            Вивчення нового матеріалу

1.         Основні поняття та визначення

1.    Статистична сукупність – набір об'єктів, що вивчаються.

2.    Вибірка – підмножина статистичної сукупності, що використовується для аналізу.

3.    Генеральна сукупність – повний набір об'єктів, що підлягають вивченню.

2.         Характеристики вибірки 1. Середні величини:

•        Середнє арифметичне (mean) – сума всіх значень, поділена на кількість значень.

•        Медіана (median) – середнє значення впорядкованої вибірки.

•        Мода (mode) – найбільш часто повторюване значення у вибірці.

2. Показники варіації:

•             Дисперсія (variance) – середнє значення квадратів відхилень від середнього.

•             Стандартне відхилення (standard deviation) – квадратний корінь з дисперсії.

•             Коефіцієнт варіації (coefficient of variation) – відношення стандартного відхилення до середнього значення, виражене у відсотках.

3.         Моменти варіаційного ряду

1.              Початкові моменти – моменти, обчислені від початку координат.

2.              Центральні моменти – моменти, обчислені від середнього значення.

4.         Методи оцінки параметрів

1. Точкові оцінки – оцінки параметрів генеральної сукупності на основі вибірки.

•             Несміщена оцінка – оцінка, математичне сподівання якої дорівнює оцінюваному параметру.

•             Ефективна оцінка – оцінка, що має мінімальну дисперсію серед всіх несміщених оцінок.

2. Інтервальні оцінки – методи визначення інтервалу, в якому з певною ймовірністю знаходиться параметр генеральної сукупності.

         Довірчий інтервал – інтервал, що з ймовірністю 1−1−α містить істинне значення параметра.

5.         Перевірка статистичних гіпотез

1.              Нульова гіпотеза (H0) – припущення, що параметр генеральної сукупності має певне значення.

2.              Альтернативна гіпотеза (H1) – припущення, що заперечує нульову гіпотезу.

3.              Критерій перевірки гіпотез – правило, на основі якого приймається рішення про відхилення чи не відхилення нульової гіпотези. Практичні завдання

1.       Розрахунок середнього арифметичного, медіани та моди для вибірки.

2.       Обчислення дисперсії та стандартного відхилення.

3.       Побудова довірчого інтервалу для середнього значення.

4.       Перевірка нульової гіпотези на основі вибіркових даних.

V.                Розв’язування вправ і задач на засвоєння

Вправа 1: Розрахунок середнього арифметичного

Завдання: Дано вибірку з п'яти значень: 5, 7, 8, 6, 9. Знайти середнє арифметичне.

Розв'язок: 

Відповідь: Середнє арифметичне значення вибірки дорівнює 7.

Вправа 2: Обчислення медіани

Завдання: Дано вибірку з шести значень: 10, 2, 7, 8, 3, 9. Знайти медіану.

Розв'язок:

1.       Впорядкуємо значення у зростаючому порядку: 2, 3, 7, 8, 9, 10.

2.       Оскільки кількість значень парна, медіана дорівнює середньому арифметичному двох середніх значень: 

       Відповідь: Медіана вибірки дорівнює                                                 7.5.

Вправа 3: Обчислення дисперсії та стандартного відхилення

Завдання: Дано вибірку: 4, 8, 6, 5, 9. Знайти дисперсію та стандартне відхилення.

Розв'язок:

1.       Обчислимо середнє арифметичне: 

2.       Знайдемо відхилення кожного значення від середнього, піднесемо їх до квадрату і обчислимо суму:

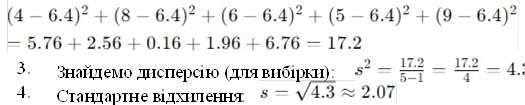
Відповідь: Дисперсія вибірки дорівнює 4.3, стандартне відхилення – 2.07. Вправа 4: Перевірка нульової гіпотези

Завдання: Відомо, що середній зріст студентів університету становить 170 см. Для вибірки з 25 студентів середній зріст склав 172 см, стандартне відхилення – 5 см. Перевірити гіпотезу про те, що середній зріст студентів дорівнює 170 см на рівні значущості 0.05.

Розв'язок:

1. 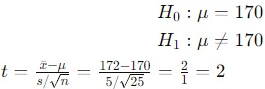      Формулюємо нульову та альтернативну гіпотези: 

 

2.       Обчислимо тестову статистику: 

 

3.       Для рівня значущості 0.05 і 24 ступенів свободи критичне значення t (двостороннє) приблизно дорівнює 2.064.

4.       Порівняємо значення тестової статистики з критичним значенням: Оскільки 2<2.064, ми не відхиляємо нульову гіпотезу.

Відповідь: Немає підстав відхиляти нульову гіпотезу на рівні значущості

0.05, середній зріст студентів можна вважати рівним 170 см. VI. Домашнє завдання 1. Виконати   інтерактивну        вправу        за       посиланням: https://learningapps.org/view16131448  

2.                    Дано вибірку з десяти значень: 12, 15, 14, 10, 13, 18, 16, 17, 11, 19.

•      Обчисліть середнє арифметичне.

•      Знайдіть медіану.

•      Визначте моду, якщо вона існує.

3.                    Середній час виконання завдання для робітників складає 50 хвилин. Вибірка з 16 робітників показала середній час виконання завдання 52 хвилини з стандартним відхиленням 5 хвилин. Перевірте гіпотезу, що середній час виконання завдання не відрізняється від 50 хвилин на рівні значущості 0.05.

VII. Рефлексія…