Самостійні роботи з алгебри 7 клас
Архів містить самостійні роботи з математики у 2 варіантах по дві самостійні роботи з кожної теми. Роздруковуються на обох сторонах аркуша, розрізаються та роздаються по одному на парту.
7 класс тема 1 с.р. №1
|
1 варіант
1.Розв’язати рівняння: 1) І2хІ=0; 2) І3хІ= - 2; 3) -5х=15.(3б)
2.Спростити вираз: 4х-5(у-х). (2б)
3.Розв’язати рівняння: 2+3 (х+1) = 4+5 (х-2). (2б)
4.Знайти значення виразу 2х –3(1 –у) + 4у при х= -2, у= 5. (2б)
5.Довести тотожність: 3с –(5 –11с) –6с + 5 = 8с. (3б)
|
2 варіант
1.Розв’язати рівняння: 1) І7хІ=0; 2) І12хІ= - 4; 3) -3х=9.(3б)
2.Спростити вираз: 7а+3(-2а+b); (2б)
3.Розв’язати рівняння: 2х-(х+2) = 5+3(х-4) (2б)
4.Знайти значення виразу 5(-4х + 0,6) + 17,5х –0,5 при х=0,8 (2б)
5.Довести тотожність: 7(4 –а) -3( -3а + 1) –25 = 2а. (3б) |
7 класс тема 1 с.р. №1
|
1 варіант
1.Розв’язати рівняння: 1) І2хІ=0; 2) І3хІ= - 2; 3) -5х=15.(3б)
2.Спростити вираз: 4х-5(у-х). (2б)
3.Розв’язати рівняння: 2+3 (х+1) = 4+5 (х-2). (2б)
4.Знайти значення виразу 2х –3(1 –у) + 4у при х= -2, у= 5. (2б)
5.Довести тотожність: 3с –(5 –11с) –6с + 5 = 8с. (3б)
|
2 варіант
1.Розв’язати рівняння: 1) І7хІ=0; 2) І12хІ= - 4; 3) -3х=9.(3б)
2.Спростити вираз: 7а+3(-2а+b); (2б)
3.Розв’язати рівняння: 2х-(х+2) = 5+3(х-4) (2б)
4.Знайти значення виразу 5(-4х + 0,6) + 17,5х –0,5 при х=0,8 (2б)
5.Довести тотожність: 7(4 –а) -3( -3а + 1) –25 = 2а. (3б) |
7 класс тема 1 с.р. №1
|
1 варіант
1.Розв’язати рівняння: 1) І2хІ=0; 2) І3хІ= - 2; 3) -5х=15.(3б)
2.Спростити вираз: 4х-5(у-х). (2б)
3.Розв’язати рівняння: 2+3 (х+1) = 4+5 (х-2). (2б)
4.Знайти значення виразу 2х –3(1 –у) + 4у при х= -2, у= 5. (2б)
5.Довести тотожність: 3с –(5 –11с) –6с + 5 = 8с. (3б)
|
2 варіант
1.Розв’язати рівняння: 1) І7хІ=0; 2) І12хІ= - 4; 3) -3х=9.(3б)
2.Спростити вираз: 7а+3(-2а+b); (2б)
3.Розв’язати рівняння: 2х-(х+2) = 5+3(х-4) (2б)
4.Знайти значення виразу 5(-4х + 0,6) + 17,5х –0,5 при х=0,8 (2б)
5.Довести тотожність: 7(4 –а) -3( -3а + 1) –25 = 2а. (3б) |
7 класс тема 1 с.р. №1
|
1 варіант
1.Розв’язати рівняння: 1) І2хІ=0; 2) І3хІ= - 2; 3) -5х=15.(3б)
2.Спростити вираз: 4х-5(у-х). (2б)
3.Розв’язати рівняння: 2+3 (х+1) = 4+5 (х-2). (2б)
4.Знайти значення виразу 2х –3(1 –у) + 4у при х= -2, у= 5. (2б)
5.Довести тотожність: 3с –(5 –11с) –6с + 5 = 8с. (3б)
|
2 варіант
1.Розв’язати рівняння: 1) І7хІ=0; 2) І12хІ= - 4; 3) -3х=9.(3б)
2.Спростити вираз: 7а+3(-2а+b); (2б)
3.Розв’язати рівняння: 2х-(х+2) = 5+3(х-4) (2б)
4.Знайти значення виразу 5(-4х + 0,6) + 17,5х –0,5 при х=0,8 (2б)
5.Довести тотожність: 7(4 –а) -3( -3а + 1) –25 = 2а. (3б) |
7 класс тема 1 с.р. №2
|
1 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
3) |
2 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
|
7 класс тема 1 с.р. №2
|
1 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
3) |
2 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
|
7 класс тема 1 с.р. №2
|
1 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
3) |
2 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
|
7 класс тема 1 с.р. №2
|
1 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
3) |
2 варіант
1. Обчислити:
3. Спростити вираз: 1) 2)
|
7 клас тема 2 с.р. №1
Варіант 1
- Спростити вираз
-
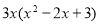 ; 2)
; 2) 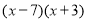 ;
;
-
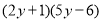 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №1
Варіант 1
- Спростити вираз
-
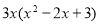 ; 2)
; 2) 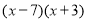 ;
;
-
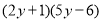 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №1
Варіант 1
- Спростити вираз
-
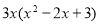 ; 2)
; 2) 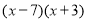 ;
;
-
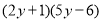 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №1
Варіант 2
- Спростити вираз
-
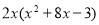 ; 2)
; 2) 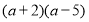 ;
;
-
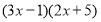 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №1
Варіант 2
- Спростити вираз
-
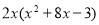 ; 2)
; 2) 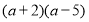 ;
;
-
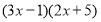 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №1
Варіант 2
- Спростити вираз
-
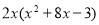 ; 2)
; 2) 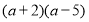 ;
;
-
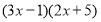 .
.
- Розкрити дужки та привести подібні
![]() .
.
- Розв’яжіть рівняння
![]() .
.
- Доведіть тотожність:
![]() .
.
7 клас тема 2 с.р. №2 Варіант 1
- Винесіть спільний множник за дужки:
-
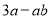 ;
;
-
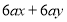 ;
;
-
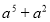 ;
;
-
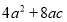 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
7 клас тема 2 с.р. №2 Варіант 1
- Винесіть спільний множник за дужки:
-
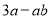 ;
;
-
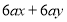 ;
;
-
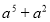 ;
;
-
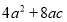 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
7 клас тема 2 с.р. №2 Варіант 1
- Винесіть спільний множник за дужки:
-
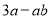 ;
;
-
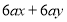 ;
;
-
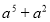 ;
;
-
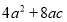 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
7 клас тема 2 с.р. №2 Варіант 2
- Винесіть спільний множник за дужки:
-
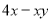 ;
;
-
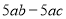 ;
;
-
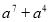 ;
;
-
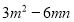 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
7 клас тема 2 с.р. №2 Варіант 2
- Винесіть спільний множник за дужки:
-
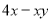 ;
;
-
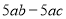 ;
;
-
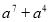 ;
;
-
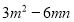 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
7 клас тема 2 с.р. №2 Варіант 2
- Винесіть спільний множник за дужки:
-
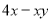 ;
;
-
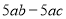 ;
;
-
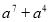 ;
;
-
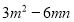 .
.
2. Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() .
.
- Розкладіть на множники:
1)![]() ;
;
2) ![]() ;
;
3) ![]()
Сам. Роб. № 1 Варіант 1
1. Розкрити дужки:
а) (a – 2)2; б) (3a +2b)2;
в) (x–2)(x+ 2) ; г) (4n +7)(4n - 7).
2. Спростіть: (2x + 3)(2x –3) – (2x –5)2 –10x
3. Розв’яжіть рівняння:
(2y –1)2 – 4(y–2)(y+2) = –5y +18
Сам. Роб. № 1 Варіант 1
1. Розкрити дужки:
а) (a – 2)2; б) (3a +2b)2;
в) (x–2)(x+ 2) ; г) (4n +7)(4n - 7).
2. Спростіть: (2x + 3)(2x –3) – (2x –5)2 –10x
3. Розв’яжіть рівняння:
(2y –1)2 – 4(y–2)(y+2) = –5y +18
Сам. Роб. № 1 Варіант 1
1. Розкрити дужки:
а) (a – 2)2; б) (3a +2b)2;
в) (x–2)(x+ 2) ; г) (4n +7)(4n - 7).
2. Спростіть: (2x + 3)(2x –3) – (2x –5)2 –10x
3. Розв’яжіть рівняння:
(2y –1)2 – 4(y–2)(y+2) = –5y +18
Сам. Роб. № 1 Варіант 1
1. Розкрити дужки:
а) (a – 2)2; б) (3a +2b)2;
в) (x–2)(x+ 2) ; г) (4n +7)(4n - 7).
2. Спростіть: (2x + 3)(2x –3) – (2x –5)2 –10x
3. Розв’яжіть рівняння:
(2y –1)2 – 4(y–2)(y+2) = –5y +18
Сам. Роб. № 1 Варіант 2
1. Розкрити дужки:
а) (a + 3)2; б) (2x – 5)2
в) (x–3)(x+ 3) ; г) ( 4n +3)(4n - 3).
2. Спростіть: (2k – 3)(2k + 3) – (3k – 5)2 – 30k
3. Розв’яжіть рівняння:
(3y + 1)2 – 9(y +1)(y – 1)= 8y – 16
Сам. Роб. № 1 Варіант 2
1. Розкрити дужки:
а) (a + 3)2; б) (2x – 5)2
в) (x–3)(x+ 3) ; г) ( 4n +3)(4n - 3).
2. Спростіть: (2k – 3)(2k + 3) – (3k – 5)2 – 30k
3. Розв’яжіть рівняння:
(3y + 1)2 – 9(y +1)(y – 1)= 8y – 16
Сам. Роб. № 1 Варіант 2
1. Розкрити дужки:
а) (a + 3)2; б) (2x – 5)2
в) (x–3)(x+ 3) ; г) ( 4n +3)(4n - 3).
2. Спростіть: (2k – 3)(2k + 3) – (3k – 5)2 – 30k
3. Розв’яжіть рівняння:
(3y + 1)2 – 9(y +1)(y – 1)= 8y – 16
Сам. Роб. № 1 Варіант 2
1. Розкрити дужки:
а) (a + 3)2; б) (2x – 5)2
в) (x–3)(x+ 3) ; г) ( 4n +3)(4n - 3).
2. Спростіть: (2k – 3)(2k + 3) – (3k – 5)2 – 30k
3. Розв’яжіть рівняння:
(3y + 1)2 – 9(y +1)(y – 1)= 8y – 16
Сам. Роб. № 2 Варіант 1
1. Представити у вигляді квадрата двочлена:
а) 4а²+4аb+b²; б) 9а²-6аb+b²
2. Розкласти на множники:
а) 49т2 – 25п2; б) ![]() ;
;
в) (7х – 4)![]()
![]()
![]() - 4а
- 4а![]() в + 2а
в + 2а![]() в
в![]() .
.
Сам. Роб. № 2 Варіант 1
1. Представити у вигляді квадрата двочлена:
а) 4а²+4аb+b²; б) 9а²-6аb+b²
2. Розкласти на множники:
а) 49т2 – 25п2; б) ![]() ;
;
в) (7х – 4)![]() - 25; г) 2а
- 25; г) 2а![]() - 4а
- 4а![]() в + 2а
в + 2а![]() в
в![]() .
.
Сам. Роб. № 2 Варіант 1
1. Представити у вигляді квадрата двочлена:
а) 4а²+4аb+b²; б) 9а²-6аb+b²
2. Розкласти на множники:
а) 49т2 – 25п2; б) ![]() ;
;
в) (7х – 4)![]() - 25; г) 2а
- 25; г) 2а![]() - 4а
- 4а![]() в + 2а
в + 2а![]() в
в![]() .
.
Сам. Роб. № 2 Варіант 1
1. Представити у вигляді квадрата двочлена:
а) 4а²+4аb+b²; б) 9а²-6аb+b²
2. Розкласти на множники:
а) 49т2 – 25п2; б) ![]() ;
;
в) (7х – 4)![]() - 25; г) 2а
- 25; г) 2а![]() - 4а
- 4а![]() в + 2а
в + 2а![]() в
в![]() .
.
Сам. Роб. № 2 Варіант 2
1. Представити у вигляді квадрата двочлена:
а) а²-6аb+9b²; б) 16а²+8аb+b²
2. Розкласти на множники:
а) 9т2 – 16п2; б) ![]() ;
;
в) (9х + 7)![]()
![]()
![]() + 6х
+ 6х![]() у + 3х
у + 3х![]() у
у![]() .
.
Сам. Роб. № 2 Варіант 2
1. Представити у вигляді квадрата двочлена:
а) а²-6аb+9b²; б) 16а²+8аb+b²
2. Розкласти на множники:
а) 9т2 – 16п2; б) ![]() ;
;
в) (9х + 7)![]()
![]()
![]() + 6х
+ 6х![]() у + 3х
у + 3х![]() у
у![]() .
.
Сам. Роб. № 2 Варіант 2
1. Представити у вигляді квадрата двочлена:
а) а²-6аb+9b²; б) 16а²+8аb+b²
2. Розкласти на множники:
а) 9т2 – 16п2; б) ![]() ;
;
в) (9х + 7)![]()
![]()
![]() + 6х
+ 6х![]() у + 3х
у + 3х![]() у
у![]() .
.
Сам. Роб. № 2 Варіант 2
1. Представити у вигляді квадрата двочлена:
а) а²-6аb+9b²; б) 16а²+8аb+b²
2. Розкласти на множники:
а) 9т2 – 16п2; б) ![]() ;
;
в) (9х + 7)![]()
![]()
![]() + 6х
+ 6х![]() у + 3х
у + 3х![]() у
у![]() .
.
Сам. Роб. № 1 Варіант 1
1.Функцію задано формулою ![]() Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
5 |
-3 |
|
|
|
у |
|
|
6 |
-4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 1 Варіант 1
1.Функцію задано формулою ![]() Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
5 |
-3 |
|
|
|
у |
|
|
6 |
-4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 1 Варіант 1
1.Функцію задано формулою ![]() Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
Знайдіть: а) у(-1), у(1); б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
5 |
-3 |
|
|
|
у |
|
|
6 |
-4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 1 Варіант 2
1.Функцію задано формулою ![]() . Знайдіть: а) у(-1), у(1);
. Знайдіть: а) у(-1), у(1);
б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
-5 |
3 |
|
|
|
у |
|
|
-6 |
4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 1 Варіант 2
1.Функцію задано формулою ![]() . Знайдіть: а) у(-1), у(1);
. Знайдіть: а) у(-1), у(1);
б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
-5 |
3 |
|
|
|
у |
|
|
-6 |
4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 1 Варіант 2
1.Функцію задано формулою ![]() . Знайдіть: а) у(-1), у(1);
. Знайдіть: а) у(-1), у(1);
б) значення аргументу, при якому у(х) = -1, у(х) = 1;
в) заповніть порожні клітинки таблиці для даної функції.
|
х |
-5 |
3 |
|
|
|
у |
|
|
-6 |
4 |
2.Знайдіть область визначення функції, яка задана формулою: а) ![]() ; б)
; б) ![]() .
.
Сам. Роб. № 2 Варіант 1
1. Побудуйте графік функції у = – 3х + 5
2. На одній координатній площині побудуйте графіки функцій у = х та у = – 2х + 3. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
Сам. Роб. № 2 Варіант 1
1. Побудуйте графік функції у = – 3х + 5
2. На одній координатній площині побудуйте графіки функцій у = х та у = – 2х + 3. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
Сам. Роб. № 2 Варіант 1
1. Побудуйте графік функції у = – 3х + 5
2. На одній координатній площині побудуйте графіки функцій у = х та у = – 2х + 3. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
х + 3 з’ясувати, чи проходить цей графік через точку:а) (0; - 3); б) (12; 6); в) (- 12; 1); г) (6; 3).
Сам. Роб. № 2 Варіант 2
1. Побудуйте графік функції у = –5х + 3.
2. На одній координатній площині побудуйте графіки функцій у = – х та у = 2х – 3.. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
Сам. Роб. № 2 Варіант 2
1. Побудуйте графік функції у = –5х + 3.
2. На одній координатній площині побудуйте графіки функцій у = – х та у = 2х – 3.. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
Сам. Роб. № 2 Варіант 2
1. Побудуйте графік функції у = –5х + 3.
2. На одній координатній площині побудуйте графіки функцій у = – х та у = 2х – 3.. Знайдіть точку перетину цих графіків.
3. Не виконуючи побудови графіка функції у = ![]() х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
х – 3 з’ясувати, чи проходить цей графік через точку: а) (6; 3); б) (12; 6); в) (- 12; 1); г) (0; - 3).
Сам. Роб. № 1 Варіант 1
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 1
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 1
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 1
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 2
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 2
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 2
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 1 Варіант 2
Розв'яжіть систему рівнянь:
а) графічним способом: ![]()
б) способом підстановки: ![]()
в) способом додавання: ![]()
Сам. Роб. № 2 Варіант 1
1. У перший день продали х кг картоплі, а в другій у кг. Складіть систему рівнянь з двома змінними за такою умовою:
всього за два дні продали 164 кг картоплі, а
різниця між кількістю картоплі, проданої у перший і другий дні, дорівнює 18 кг.
2. Сума двох чисел дорівнює 92, а їх різниця дорівнює 16. Знайдіть ці числа.
3. Три яблука і дві груші важать разом 1200 г, а два яблука і три груші важать 1300 г. Скільки важить яблуко і скільки важить груша?
Сам. Роб. № 2 Варіант 1
1. У перший день продали х кг картоплі, а в другій у кг. Складіть систему рівнянь з двома змінними за такою умовою:
всього за два дні продали 164 кг картоплі, а
різниця між кількістю картоплі, проданої у перший і другий дні, дорівнює 18 кг.
2. Сума двох чисел дорівнює 92, а їх різниця дорівнює 16. Знайдіть ці числа.
3. Три яблука і дві груші важать разом 1200 г, а два яблука і три груші важать 1300 г. Скільки важить яблуко і скільки важить груша?
Сам. Роб. № 2 Варіант 1
1. У перший день продали х кг картоплі, а в другій у кг. Складіть систему рівнянь з двома змінними за такою умовою:
всього за два дні продали 164 кг картоплі, а
різниця між кількістю картоплі, проданої у перший і другий дні, дорівнює 18 кг.
2. Сума двох чисел дорівнює 92, а їх різниця дорівнює 16. Знайдіть ці числа.
3. Три яблука і дві груші важать разом 1200 г, а два яблука і три груші важать 1300 г. Скільки важить яблуко і скільки важить груша?
Сам. Роб. № 2 Варіант 1
1. У перший день продали х кг картоплі, а в другій у кг. Складіть систему рівнянь з двома змінними за такою умовою:
всього за два дні продали 164 кг картоплі, а
різниця між кількістю картоплі, проданої у перший і другий дні, дорівнює 18 кг.
2. Сума двох чисел дорівнює 92, а їх різниця дорівнює 16. Знайдіть ці числа.
3. Три яблука і дві груші важать разом 1200 г, а два яблука і три груші важать 1300 г. Скільки важить яблуко і скільки важить груша?
Сам. Роб. № 2 Варіант 1
1. На верхній полиці х книг, а на нижній у книг. Складіть систему рівнянь з двома змінними за такою умовою: всього на полицях 112 книг, а на верхній полиці на 36 книг більше, ніж на нижній.
2. Сума двох чисел дорівнює 17, а їх різниця дорівнює 7. Знайдіть ці числа.
3. Сім альбомів і два зошити коштують разом 111 грн., а п'ять альбомів і три зошити коштують 84 грн.. Скільки коштує один альбом і скільки коштує одна зошит?
Сам. Роб. № 2 Варіант 1
1. На верхній полиці х книг, а на нижній у книг. Складіть систему рівнянь з двома змінними за такою умовою: всього на полицях 112 книг, а на верхній полиці на 36 книг більше, ніж на нижній.
2. Сума двох чисел дорівнює 17, а їх різниця дорівнює 7. Знайдіть ці числа.
3. Сім альбомів і два зошити коштують разом 111 грн., а п'ять альбомів і три зошити коштують 84 грн.. Скільки коштує один альбом і скільки коштує одна зошит?
Сам. Роб. № 2 Варіант 1
1. На верхній полиці х книг, а на нижній у книг. Складіть систему рівнянь з двома змінними за такою умовою: всього на полицях 112 книг, а на верхній полиці на 36 книг більше, ніж на нижній.
2. Сума двох чисел дорівнює 17, а їх різниця дорівнює 7. Знайдіть ці числа.
3. Сім альбомів і два зошити коштують разом 111 грн., а п'ять альбомів і три зошити коштують 84 грн.. Скільки коштує один альбом і скільки коштує одна зошит?
Сам. Роб. № 2 Варіант 1
1. На верхній полиці х книг, а на нижній у книг. Складіть систему рівнянь з двома змінними за такою умовою: всього на полицях 112 книг, а на верхній полиці на 36 книг більше, ніж на нижній.
2. Сума двох чисел дорівнює 17, а їх різниця дорівнює 7. Знайдіть ці числа.
3. Сім альбомів і два зошити коштують разом 111 грн., а п'ять альбомів і три зошити коштують 84 грн.. Скільки коштує один альбом і скільки коштує одна зошит?
-
Дякую!


про публікацію авторської розробки
Додати розробку
