Семінар - урок " Квадратична функція, її графік і властивості".

Семінар – урок

      Алгебра, 9 клас, тема: "Квадратична функція, її графік і властивості»

Мета. 1. Узагальнити і систематизувати знання про квадратичну функцію і її властивості. Учити застосовувати отримані знання при рішенні вправ і завдань.

2. Розвивати творчу і розумову діяльність учнів. Сприяти умінню чітко і ясно висловлювати свої думки.

3. Формувати вміння відбирати й використовувати потрібні знання та способи діяльності, застосовувати способи взаємодії з партнерами.

                                                                    План уроку

1. Підготовка до семінару.

     План семінару, додаткові питання учням повідомляються за два тижні до уроку. Упродовж цього часу проводяться консультації.

План семінару.   1) Квадратична функція і її властивості.

                                2) Історія виникнення і розвиток поняття функції.

                                3) Різні способи побудови графіку квадратичної функції.

                              Література

1. А. Г. Мерзляк, В. Б. Полонський, М. С. Якір.- Х,: Гімназія. 2017.
2. С. П. Бабенко. Алгебра. 9 клас. Експрес контроль. Видавництво «Ранок» 2009 рік
3. Г. І. Глейзер «Історія математики в школі»-М. : Просвещение,1982

(Вчитель призначає відповідальних (зазвичай з числа добре успішних учнів), які з урахуванням побажань однокласників формують робочі групи (по 4-5 чоловік). При цьому важливо проконтролювати, щоб групи були приблизно рівні по знанням, по кількісному складу і щоб до них увійшли усі члени класного колективу).

1. Вчитель

 Мудрець сказав: «Дві людини, які обмінялися золотими монетами, не стали багатшими. Але якщо вони  обмінялися думками, то кожен з них став вдвоє багатшим. Адже обидва стали тепер розумнішими.»

• Ця притча проста, але зміст її глибокий. Обмінюючись думками, ідеями, досвідом, знаннями, люди нічого не втрачають, а тільки набувають нові знання.

Ось і ви сьогодні дізнаєтесь нове про квадратичну функцію. Я сподіваюсь, що кожен із вас буде уважним та активним.

2. Вчитель та його помічник

а) Фронтальне опитування.

1. Дати означення  квадратичної функції.
2. Дати означення області визначення функції.
3. Дати означення множини значень функції.
4. Дати означення графіка функції.
5. Дати означення зростаючої функції.
6. Дати означення спадної функції.
7. Дати означення нулів функції.
8. Як знайти координати вершини параболи?
9. Як виділити повний квадрат двочлена?

 

б) Самостійна робота.

 І варіант                                                                                       ІІ варіант

 

1. Визначити який знак має  а, перший коефіцієнт квадратичної функції.
2. Визначити координати вершини параболи.
3. Знайти нулі функції.
4. Знайти проміжки зростання та спадання функції.

3. Другий учень та його група.

Історична довідка

Функція - одне з найбільш важливих понять сучасної математики. Воно виникло в ХVІІ столітті. Спочатку Р. Декарт ввів поняття змінної величини і систему координат, став розглядати залежність ординат точок графіка від їх абсцис. Слово "функція" для назви таких залежностей в перше ввів німецький математик Г. Лейбніц (1646 - 1716). Швейцарський математик Л. Ейлер (1707 - 1716) функцією називав вираз, що складається з змінних і чисел. Наприклад 3х - 5 - функція від змінної х, оскільки значення цього виразу залежить від значень х. Це поняття зусиллями багатьох математиків уточнювалося, розширювалося, наповнювалося новим змістом. Українські математики теж зробили свій внесок. Так хотілося згадати видатного українського математика М. П .  Кравчука.

       Кравчук М. П. (1982 – 1942)- один із засновників Інституту математики Академії наук УРСР, вніс фундаментальний вклад у різні галузі математики, а саме: алгебру, теорію чисел, теорію функцій, теорію диференціальних та інтегральних рівнянь, теорію ймовірностей, математичну статистику. М.П. Кравчук – автор понад 180 наукових праць, у тому числі 10 монографій. Широко відомими у світовій математичній літературі стали наукові терміни, що носять його ім’я, такі, як ”многочлени і q-многочлени Кравчука”, ”q-функції Кравчука-Мейкснера”. Він по праву вважається одним із найвидатніших алгебраїстів 1-ої половини 20-го ст.

М. П. Кравчук  (1892-1942)      Г. В. Лейбніц (1646- 1716)  Р.  Декарт (1596- 1650)
4.Третій учень та його група

Різні  способи побудови графіка квадратичної функції.

Розв’язуємо вправу разом.

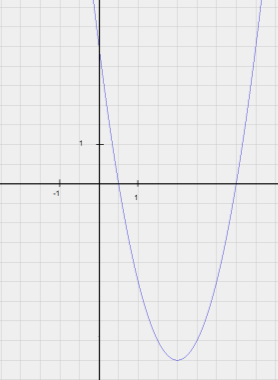
1. Побудуйте графік функциії: У = 2X² - 4X- 6.

 

Розглянемо квадратичну функцію У = 2X² - 4X- 6. Виділимо квадрат двочлена:                                                                                     

У = 2X² - 4X- 6= 2 (Х² – 2Х + 1 – 3 - 1) = 2 (Х – 1)² – 8.

Отже графік функції у = 2х² спочатку потрібно змістити паралельним перенесенням на 1 одиницю вправо, а потім на 8 одиниці вниз.

 

 

 

 

     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

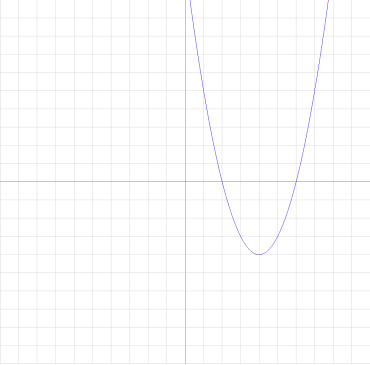
2. Даний графік можна було побудувати і іншим способом: перенести систему координат у вершину параболи (1; - 8) і в новій  системі координат побудувати графік функції у = х².

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язуємо вправу разом.

3. Можна будувати графік квадратичної функції У = 2X² - 4X- 6, і без виділення повного квадрата за наступним алгоритмом:

1.  а>0, то вітки вгору, якщо а<0, то вітки вниз.
2. Знаходимо нулі функції  (точки перетину графіка з віссю ОХ) – корені квадратного рівняння ах² + bх + с = 0.

2X² - 4X- 6 =0,

X² - 2X- 3 =0,

                     Х₁ = -1; Х₂ = 3,   (-1; 0); (3; 0).   

3. Знаходимо абсцису вершини параболи

                          Х₀ = - , (1;-8).

                           У₀ = 2 ·1² –4 –6 = -8.

4. Знаходимо точку перетину параболи з віссю ОУ: У = с.  У = - 6.
5. Знайдемо декілька допоміжних точок:

Х     0    2

У      -6  -6  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язуємо вправу разом.

4. Побудуємо графік функції  У= 2Х² – 4Х або  У = Х (2Х - 4).  Нулі функції - Х = 0; Х = 2. Ці точки симетричні відносно осі параболи, яку необхідно побудувати, тому абсциса її вершини Х = 1. Ордината її                                                                  У = 1 ∙ (2 - 4) = - 2. Відмітимо її на координатній площині. Через позначені три точки проходить графік функції У= 2Х² - 4Х. Перенесемо його на 6 одиниць вниз, отримаємо графік функції У = 2x² - 4x- 6.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Робота з картками. Оберіть спосіб, який вам до вподоби, виконайте самостійну роботу.

І варіант	ІІ варіант	ІІІ варіант
Побудувати графік функції  у = -х2 - 4х - 3 та вказати  E(y), проміжки зростанні та спадання, проміжки знакосталості функції.	Побудувати графік функції  у = -х2 - 2х - 4 та вказати  E(y), проміжки зростанні та спадання, проміжки знакосталості функції.	Побудувати графік функції    у = -х2 - 6х - 8 та вказати  E(y), проміжки зростанні та спадання, проміжки знакосталості функції.

 

III. Додому

1.  Визначити напрям віток, знайти координати вершини і побудувати схематично графік квадратичної функції  у = х² - 10х + 20.
2. Побудувати графік функції у = -0,2х² + 2х – 5. Знайти нулі функції та значення х, при яких f(х)= -5.

 

 

ІV. Висновок

 Вивчивши способи геометричних перетворень графіків функцій, можна побудувати графік будь-якої алгебраїчної функції, рівняння якої утворене з найпростіших функцій. Сьогодні ми розглянули функцію, рівняння якої можна утворити з графіка у = х² , шляхом геометричних перетворень - квадратичну функцію.