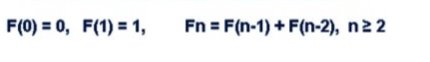
РОЗДІЛ ДЛЯ ФАКУЛЬТАТИВУ З МАТЕМАТИКИ 10 КЛАС:

«ЧИСЛА ФІБОНАЧЧІ»

КАЛЕНДАРНО-ТЕМАТИЧНЕ ПЛАНУВАННЯ

Всього годин: 15

З них резервних: 1

№ з/п	Тема уроку	Дата проведення	Примітки
1	Задача про кроликів. Історія появи чисел Фібоначчі		+
2	Життєвий шлях та наукові здобутки Леонарда Пізанського		+
3	Математичний запис чисел Фібоначчі. Поняття рекурсії		+
4	Формула Біне та інші способи запису чисел Фібоначчі, властивості чисел Фібоначчі. Період Пізано.		+
5	Розв’язування задач олімпіадного програмування, які опираються на властивості чисел Фібоначчі		+
6	Практична робота : «Аналіз алгоритмів виведення чисел Фібоначчі. Розв’язування олімпіадних задач »		+
7	Розв’язування олімпіадних завдань з математики, які опираються на властивості чисел Фібоначчі
8	Числа Фібоначчі – Нарайни, та їхні властивості. Числа Фібоначчі та їх зв’язок з трикутником Паскаля
9	Золотий переріз та його зв’язок з числами Фібоначчі. Використання золотого перерізу. Принцип Діріхле та числа Фібоначчі
10	Теорема Цикенфорда та її доведеня
11	Фібоначева система числення
12	Використання чисел Фібоначчі у природі
13	Використання чисел Фібоначчі у економіці
14	Захист проектів на тему: «Інші цікаві факти про послідовність і числа Фібоначчі»		+
15	Резервний урок		+

 

Навчальні досягнення учнів

Учень(учениця): Користується властивостями чисел Фібоначчі, чисел Фібоначчі – Нарайни, принципом Діріхле, правилов піднесення до степення за допомогою трикутника Паскаля та рекурсією при розв’язані олімпіадних задач з математики та програмування. Усвідомлює важливість чисел Фібоначчі та їх властивостей в математиці та в оточуючому світі, необхідність використання принципа Діріхле при розв’язанні прикладних задач Використовує властивості чисел Фібоначчі в образотворчому мистецтві і в архітектурі.

Учень(учениця): Розпізнає числа Фібоначчі або числа Фібоначчі - Нарайни серед набору випадкових чисел, формулу Біне, означення та доведення теореми Цикенфорда, запис золотого перерізу, базову схему програми з використанням рекурсії. Будує зображення ідеального прямокутника та золотої спіралі, зображення трикутника Паскаля Обчислює значення n-ого члена послідовності Фібоначчі і послідоності Фібоначчі Нарайни, значення числа переведеного в фібоначеву систему числення. Встановлює властивості чисел Фібоначчі.

 

Рівні навчальних досягнень	Бали	Критерії оцінювання навчальних досягнень
I. Початковий	1	Учень (учениця) розпізнає один із кількох запропонованих математичних об’єктів та об’єктів програмування (символів, виразів, геометричних фігур тощо), виділивши його серед інших; читає і записує числа, переписує даний математичний вираз, формулу;
	2	Учень (учениця) виконує однокрокові дії з числами, найпростішими математичними виразами; реалізує найпростіші програми на учбових мовах програмування; впізнає окремі математичні об’єкти і пояснює свій вибір
	3	Учень (учениця) порівнює дані або словесно описані математичні об’єкти за їх суттєвими властивостями; за допомогою вчителя виконує елементарні завдання
II. Середній	4	Учень (учениця) відтворює означення математичних понять і формулювання тверджень; називає елементи математичних об’єктів; формулює деякі властивості математичних об’єктів; виконує за зразком завдання обов'язкового рівня
	5	Учень (учениця) ілюструє означення математичних понять та понять програмування, формулювань теорем і правил виконання математичних дій прикладами із пояснень вчителя або підручника; розв’язує завдання обов'язкового рівня за відомими алгоритмами з частковим поясненням
	6	Учень (учениця) ілюструє означення математичних понять та понять програмування, формулювань теорем і правил виконання математичних дій власними прикладами, ілюстую використання базових конструкцій програмування; самостійно розв’язує завдання обов'язкового рівня з достатнім поясненням; записує математичний вираз, або програмний код, формулу за словесним формулюванням і навпаки
III. Достатній	7	Учень (учениця) застосовує означення математичних понять та понять програмування та їх властивостей для розв’язання завдань у знайомих ситуаціях; знає залежності між елементами математичних об’єктів; самостійно виправляє вказані йому (їй) помилки; розв’язує завдання, передбачені програмою, без достатніх пояснень
	8	Учень (учениця) володіє визначеним програмою навчальним матеріалом; розв’язує завдання, передбачені програмою, з частковим поясненням; частково аргументує математичні міркування й розв’язування завдань
	9	Учень (учениця): вільно володіє визначеним програмою навчальним матеріалом; самостійно виконує завдання в знайомих ситуаціях з достатнім поясненням; виправляє допущені помилки; повністю аргументує обґрунтування математичних тверджень, та записаний високорівневою мовою програмний код ; розв’язує завдання з достатнім поясненням
IV. Високий	10	Знання, вміння й навички учня (учениці) повністю відповідають вимогам програми, зокрема: учень (учениця) усвідомлює нові для нього (неї) математичні факти, ідеї, вміє доводити передбачені програмою математичні твердження з достатнім обґрунтуванням, з достатнім обґрунтуванням розв’язую прикладну задачу за допомогою комп’ютера; під керівництвом учителя знаходить джерела інформації та самостійно використовує їх; розв’язує завдання з повним поясненням і обґрунтуванням
	11	Учень (учениця) вільно і правильно висловлює відповідні математичні міркування, переконливо аргументує їх, та з повним обґунтуванням розв’язує прикладні задачі, та узагальнює Її і реалізуює розв’язок високорівневою мовою програмування, вивчення якої передбачене програмою; самостійно знаходить джерела інформації та працює з ними; використовує набуті знання і вміння в незнайомих для нього (неї) ситуаціях; знає, передбачені програмою, основні методи розв’язання завдання і вміє їх застосовувати з необхідним обґрунтуванням
	12	Учень (учениця) виявляє варіативність мислення і раціональність у виборі способу розв’язання математичної проблеми; вміє узагальнювати й систематизувати набуті знання; здатний(а) до розв’язування нестандартних задач і вправ

 

Урок 1

Тема. Задача про кроликів. Історія появи чисел Фібоначчі.

Мета:

• навчальна: дізнатися про числа Фібоначчі і історію їх появи
• виховна: виховувати інтерес до вивчення інформатики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень вміє пояснити проблему і розв’язок задачі про кроликів, вміє тезісно розповісти історію появи сучасного Означення чисел Фібоначчі

Тип уроку: урок засвоєння нових знань.

Матеріали та обладнання: файл презентації, стенд із зображенням розв’язків задачі про кроликів.

Програмне забезпечення: MS Power Point (OpenOffice Impress)

Хід уроку

Жодна інша  наука не навчає

так ясно розуміти  гармонію природи,

як математика.                                    

                                                                                                                                   П.Карус

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Актуалізація опорних знань з теми «Послідовності»

Учні об'єднуються в 2 команди, кожна з яких презентує обраний вид послідовності: (Скінченна послідовність, нескінчена послідовність, числова послідовність, нескінченно мала і нескінченно велика послідовність), за наступним планом:

1. Спосіб запису
2. Основні властивості
3. Навести приклади

*Напевно учні виберуть числову послідовність, тоді вони будуть повинні навести властивості арифметичної і геометричної прогресії

Послідо́вність — функція визначена на множині натуральних чисел яка набуває значення на об'єктах довільної природи.{\displaystyle f\,:\;\mathbb {N} \,\rightarrow \,\!X}.

Записується у вигляді {\displaystyle \ \{x_{1},x_{2},\ldots ,x_{n},\ldots \}}, чи коротко {\displaystyle \ \{x_{n}\}}. Елементи {\displaystyle \ x_{1},x_{2},\ldots }називаються членами послідовності.

Можна розглядати послідовність як впорядковану (занумеровану натуральними числами) множину її членів.

В залежності від типу елементів, послідовності поділяють на числові та функціональні.

Наприклад: послідовність дійсних чисел — числова послідовність, яка набуває дійсних значень.

Скінченна послідовність

Вище було наведено означення нескінченної послідовності. Послідовність може визначатись на скінченній підмножині натуральних чисел, тоді вона називається скінченною. Кількість членів послідовності називають довжиною послідовності.

Скінченна послідовність на відміну від нескінченної має скінченну довжину. Також для скінченних послідовностей використовується інше позначення: {\displaystyle \{x_{i}\}_{i=1}^{n}}. У цьому випадку i — лічильник, а n — кількість елементів.

Числова послідовність

Числова́ послідо́вність  — послідовність дійсних чисел, тобто відображення, яке кожному натуральному числу n ставить у відповідність дійсне число {\displaystyle x_{n}} . Число {\displaystyle x_{n}} називають елементом або членом послідовності.

Послідовною називають функцію, яка задана на множині всіх або перших n натуральних чисел.

Числа, які утворюють послідовність називають членами послідовності.

Якщо послідовність має скінченне число членів, то її називають скінченною послідовністю.

Якщо послідовність має нескінченне число членів, то її називають нескінченною послідовністю, а у записі це показують трьома крапками після останнього записаного члена послідовності.

У загальному випадку члени послідовності, як правило, позначають малими буквами з індексами внизу. Кожний індекс вказує порядковий номер члена послідовності.

Щоб задати послідовність, потрібно вказати спосіб, за допомогою якого можна знайти будь-який його член.

1. Послідовність можна задати описом знаходження її членів.
2. Скінченну послідовність можна задати переліком її членів.
3. Послідовність можна задати таблицею, у якій навпроти кожного члена послідовності вказують його порядковий номер.
4. Послідовність можна задати формулою, за якою можна знайти будь-який член послідовності, знаючи його номер.
5. Спочатку вказати перший або кілька перших членів послідовності, а потім — умову, за якою можна визначити будь-який член послідовності за попереднім. Такий спосіб задання послідовності називають рекурентним.

Приклади

Натуральні парні числа — (2,4,6,8,10,). Функція, яка задає послідовність  {\displaystyle a_{n}=2n}.

Рекурсивне визначення — {\displaystyle a_{n}=a_{n-1}+2,a_{1}=2}

Нескінченно мала послідовність

Послідовність {\displaystyle x_{n}} називається нескінченно малою, якщо для будь-якого додатнього числа ε, можна вказати таке натуральне число N, що при n≥N, всі елементи   {\displaystyle x_{n}}задовольняють нерівність |{\displaystyle x_{n}} |<ε

Основні властивості нескінченно малих послідовностей

Сума двох нескінченно малих послідовностей є нескінченно мала послідовність.

1. Різниця двох нескінченно малих послідовностей є нескінченно мала послідовність.
2. Добуток двох нескінченно малих послідовностей є нескінченно мала послідовність.
3. Добуток нескінченно малої послідовності на дійсне число є нескінченно мала послідовність.
4. Якщо всі елементи нескінченно малої послідовності рівні певному числу c, то це число рівне нулю. ( c=0 )
5. Якщо елементи 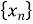{\displaystyle x_{n}}  нескінченно великої послідовності відмінні від нуля, то послідовність 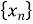{\displaystyle {\frac {1}{x_{n}}}}  є нескінченно малою.

Нескінченно велика послідовність

Послідовність {\displaystyle \{x_{n}\}} називається нескінченно великою, якщо для будь-якого додатнього числа A, знайдеться натуральне число N, що для n≥N, всі елементи {\displaystyle \{x_{n}\}} будуть задовольняти нерівність {\displaystyle |x_{n}|>A}

 

Відповідь учні викладають у вигляді малюнку і усної доповіді одного з учасників команди.

Назва виду послідовності
Способи задання	Властивості	Приклади

 

3. Вивчення нового матеріалу

Опираючись на слайди презентації і нижче поданий матеріал пояснити учням тему уроку.

 

У XIII столітті італійський математик Фібоначчі (життєпис якого ми будемо вивчати на наступному уроці) розв'язував таку задачу: Фермер годує кроликів. Кожен кролик народжує одного кролика, коли йому стає 2 місяці, а потім дає потомство в 1 кролик кожен місяць. Скільки кроликів буде у фермера через n місяців, якщо спочатку у нього був лише один (вважаємо, що кролики не гинуть і кожен народжений дає потомство за вище описаною схемою)?

Очевидно, що першого та другого місяця у фермера залишається один кролик, оскільки потомства ще немає. На третій місяць буде два кролики, оскільки перший через два місяці народить другого кролика. На четвертий місяць перший кролик дасть ще одного, а другий кролик потомства не дасть, оскільки йому ще тільки один місяць. Отож на четвертий місяць буде три кролики.

Можна помітити, що кількість кроликів після n-го місяця дорівнює кількості кроликів, які були у n-1 місяці, плюс кількість народжених кроликів. Останніх буде стільки, скільки є кроликів, що дають потомство, або дорівнює кількості кроликів, яким вже виповнилося 2 місяці (тобто кількості кроликів після n-2 місяця).

Якщо через F_n позначити кількість кроликів після n-го місяця, то має місце таке рекурентне співвідношення:

{\displaystyle F_{n}=F_{n-1}+F_{n-2},F_{1}=F_{2}=1}

Покладемо F₀ = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … ,

 

Дехто помістив пару кроликів у деяке місце, загороджене з усіх боків стіною, щоб дізнатися, скільки пар кроликів  народиться   протягом року, якщо природа кроликів така, що через місяць пара кроликів народжує другу пару, а   народжують кролики починаючи з другого місяця післясвоєї появи на світ.

 

Розв'язання цієї задачі можна наочно продемонструвати за допомогою рисунка. (вчитель пояснює зміст стенду)

 

 

 

4. ЗАКРІПЛЕННЯ

Кожен учень виходить до дошки і за порядком записує розв’язок задачі про кроликів для n-ого числа , де 1- перший учень і так далі, а готовий результат вписує в таблицю накреслену на дошці

1	2	3	4	.	.	.	.	n	n+1

 

5. ПІДВЕДЕННЯ ПІДСУМКІВ УРОКУ

Слово вчителя: Сьогодні у нас був дуже змістовний урок, більше теоретичний і я пропоную Вам відповісти на декілька питань

• Що ви дізналися сьогодні на уроці?
• Сформуйте умову і спосіб розв’язання задачі про кроликів
• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.

 

*Для оцінювання уроку:

 

6. Домашнє завдання

1. Вивчити матеріал уроку, скласти список незрозумілих питань.
2. Так, як урок був більше теоретичним, тоді я пропоную Вам розв’язати три нестандартні математичні задачі:

• Имеются каменные глыбы: 50 штук по 700 кг, 60 штук по 1000 кг и 80 штук по 1500 кг (раскалывать глыбы нельзя).

 а) Можно ли увезти все эти глыбы одновременно на 65 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?

б) Можно ли увезти все эти глыбы одновременно на 43 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?

в) Какое наименьшее количество грузовиков, грузоподъёмностью 5 тонн каждый, понадобится, чтобы вывезти все эти глыбы одновременно, предполагая, что в грузовик выбранные глыбы поместятся?

• Знайти всі цілі розв’язки рівняння 15х – 7у = 13.
• 

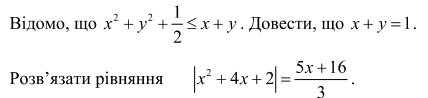
Урок 2

Тема. Життєвий шлях та наукові здобутки Леонарда Пізанського

Мета:

• навчальна: дізнатися про життєвий шлях і наукові здобутки Леонарда Пізанського, задачі поставлені Леонардом Пізанським
• виховна: виховувати інтерес до вивчення математики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень зможе тезісно розповісти хронологію життя Леонарда Пізанського, зможе розв’язувати задачі, складені Л. Фібоначчі

Тип уроку: урок засвоєння нових знань, розв’язування задач.

Матеріали та обладнання: файл презентації, стенд

 Програмне забезпечення: MS Power Point (OpenOffice Impress)

Хід уроку

Є в математиці щось, що викликає людський захват

Ф. Хаусдорф

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Вивчення нового матеріалу

Опираючись на слайди презентації і нижче поданий матеріал пояснити учням тему уроку.

 

Леона́рдо Піза́нський (італ. Leonardo Pisano, близько 1170 — близько 1250[2]), відоміший як Фібоначчі (Fibonacci) — італійський математик 13 століття, автор математичних трактатів, завдяки яким Європа довідалася про вигадану індійцями позиційну систему числення, відому зараз як арабські цифри. Леонардо розглянув також ідею так званих чисел Фібоначчі і вважається одним з найвидатніших західних математиків Середньовіччя[3].

Леонардо Пізанський найбільше відомий під прізвиськом Фібоначчі (Fibonacci); про походження цього псевдоніму є різні версії. За однією з них, його батько Гільєрмо мав прізвисько Боначчі («Добромисний»), а сам Леонардо прозивався filius Bonacci («син добромисного»). За іншою, Fibonacci походить від фрази Figlio Buono Nato Ci, що в перекладі з італійської означає «хороший син народився».

Освіта

Життя і наукова кар'єра Леонардо тісно пов'язана з розвитком європейської науки і культури. Дата його народження невідома — називаються варіанти 1170 і 1180 років.

 

Батько Фібоначчі у торгових справах часто бував у Алжирі, і Леонардо вивчав там математику у арабських учителів. Пізніше відвідав Єгипет, Сирію, Візантію, Сицилію. Леонардо вивчав праці математиків країн ісламу (таких як аль-Хорезмі і Абу Каміл); завдяки арабським перекладам він ознайомився також з досягненнями античних та індійських математиків. На основі засвоєних ним знань Фібоначчі написав ряд математичних трактатів, що являють собою видатне явище середньовічної західноєвропейської науки.

У часи Фібоначчі імператором Священної Римської імперії був Фрідріх II. Вихований у традиціях південної Італії Фрідріх ІІ був внутрішньо глибоко далекий від європейського християнського лицарства. Тому ціновані його дідом лицарські турніри Фрідріх ІІ зовсім не визнавав. Замість цього він культивував менш криваві математичні змагання, на яких супротивники обмінювалися не ударами, а задачами.

На одному з таких турнірів проявився талант Леонардо Фібоначчі. Цьому сприяла чудова освіта, яку отримав син купця Боначчі на Сході у арабських учителів.

Заступництво Фрідріха сприяло також випуску наукових трактатів Фібоначчі: «Книга абака», «Практика геометрії», «Книга квадратів»

За цими книгами, які перевершували за своїм рівнем арабські і середньовічні європейські твори, вивчали математику ледь не до часів Декарта (XVII століття).

У XIX столітті в Пізі був поставлений пам'ятник вченому.

Наукова діяльність

Значну частину засвоєних ним знань він виклав у своїй видатній "Книзі абака" (Liber abaci, 1202 ; до наших днів зберегся тільки доповнений рукопис 1228 року). Ця книга містить майже всі арифметичні й алгебраїчні відомості того часу, викладені з винятковою повнотою і глибиною. Вона відіграла значну роль у розвитку математики в Західній Європі протягом кількох наступних століть. Саме за цією книгою європейці знайомилися з арабськими цифрами. Перші п'ять розділів книги присвячено арифметиці цілих чисел на основі десяткової системи числення. У VI і VII главі Леонардо викладає дії зі звичайними дробами. У VIII—X книгах викладені прийоми розв'язання задач комерційної арифметики з використанням пропорцій. У XI главі розглянуті задачі на змішування. У XII главі наводяться задачі на підсумовування рядів — арифметичної і геометричної прогресій, ряду квадратів[4] і, вперше в історії математики, поворотного ряду[5], що у найпростішому випадку приводить до послідовності так званих чисел Фібоначчі. У XIII главі викладається правило двох помилкових положень[6] і ряд інших задач, що зводяться до лінійних рівнянь. У XIV главі Леонардо на числових прикладах роз'яснює способи наближеного добування квадратного і кубічного коренів. Нарешті, в XV главі зібраний ряд завдань на застосування теореми Піфагора і велика кількість прикладів на квадратні рівняння.

 

«Практика геометрії» (Practica geometriae, 1220) містить різноманітні теореми, пов'язані з вимірювальним методом. Поряд з класичними результатами Фібоначчі наводить свої власні — наприклад, перше доведення того, що три медіани трикутника перетинаються в одній точці (Архімеду цей факт був відомий, але якщо його доведення й існувало, то до нас воно не дійшло).

 

У трактаті «Квітка» (Flos, 1225) Фібоначчі досліджував задачу, яка в сучасних позначеннях зводиться до знаходження коренів кубічного рівняння

запропоновану йому Іоанном Палермським на математичному змаганні при дворі імператора Фрідріха II. Сам Іоанн Палермський майже напевно запозичив це рівняння з трактату Омара Хайяма «Про докази задач алгебри», де воно наводиться як приклад одного з видів у класифікації кубічних рівнянь. Леонардо Пізанський досліджував це рівняння, показавши, що його корінь не може бути раціональним або ж мати вигляд однієї з квадратичних ірраціональностей, що зустрічаються в X книзі Начал Евкліда, а потім знайшов наближене значення кореня в шістдесяткових дробах, не вказуючи, проте, способу свого розв'язку.

«Книга квадратів» (Liber quadratorum, 1225), містить ряд задач на знаходження розв'язку невизначених квадратних рівнянь. В одному із завдань, також запропонованому Іоанном Палермським, потрібно було знайти раціональне квадратне число, яке, будучи збільшеним або зменшеним на 5, знову дає раціональні квадратні числа.

 

Числа Фібоначчі

У «Книзі абака» Фібоначчі описав послідовність, названу його іменем — послідовність Фібоначчі. Ця послідовність була відома ще в Стародавній Індії, задовго до Фібоначчі. Свою нинішню назву числа Фібоначчі отримали завдяки дослідженню властивостей цих чисел. Послідовність Фібоначчі визначається як ряд чисел, в якому кожне наступне число дорівнює сумі двох попередніх:

 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …

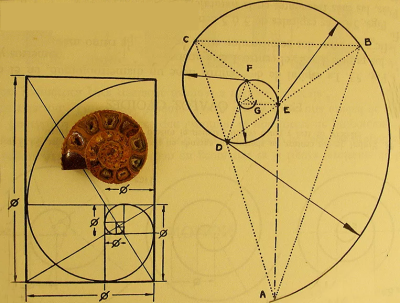
Відношення двох сусідніх чисел у послідовності Фібоначі прямує до золотого перетину, числа, відомого ще в античності.

 

У викладі Фібоначчі ця задача формулювалася як задача про число кроликів, які народжуються і виростають за алгоритмом: кожен маленький кролик на наступному кроці виростає у великого кроля, а кожен великий кріль народжує маленького. Як наслідок виникає послідовність:

к

K

Кк

КкК

КкККк

КкККкКкК

і так далі. Загальна кількість кроликів і складає послідовність Фібоначчі.

Задачі Фібоначчі

Залишаючись прихильником математичних турнірів, основну роль у своїх книгах Фібоначчі віддає задачам, їх розв'язкам і коментарям. Задачі на турніри складали як сам Фібоначчі, так і його суперник, придворний філософ Фрідріха II Йоган Палермський Задачі Фібоначчі, або їх аналоги, у подальшому використовувались у різних підручниках з математики протягом декількох століть. Їх можна зустріти в «Сума арифметики, геометрії, дробів, пропорцій і пропорційності» Л. Пачіолі (1494), в «Приємних і цікавих задачах» Клода Гаспара Баше де Мезір'яка (1612), в «Арифметиці» Леонтія Магніцького (1703), в «Алгебрі» Л.Ейлера (1768).

Праці

   « Книга абака » (Liber abaci), написана в 1202 році, але дійшла до нас у своєму другому варіанті, що відноситься до 1228 р.

   «Практика геометрії» (Practica geometriae) (1220)

   «Книга квадратів» (Liber quadratorum) (1225)

   «Квітка» (Flos, 1225)

У Пізі, в монастирі історичного кладовища, є статуя Леонардо, з написом: Ampere Leonardo Fibonacci Insigne Matematico Pisano del Secolo XII. Зображення є продуктом художньої уяви, оскільки ні портрету Леонардо, ні детального опису його зовнішньості, зробленого його сучасниками, не збереглося. Статуя була встановлена з ініціативи двох членів тимчасового уряду колишнього великого герцогства Тоскана, Козімо Рідолфі та Беттіно Рікасолі, які домоглися утвердження указу про фінансування статуї 23 вересня 1859. Роботу над статуєю доручили флорентійському скульптору Джованні Пагануччі, і він закінчив завдання у 1863 році. Статуя була поміщена в Пізі на Кампо-Санто, де знаходиться могила Леонардо.

 

У 1926 році, коли при владі в Італії перебували фашисти, влада вирішила перенести пам'ятник Леонардо та дві статуї інших відомих громадян міста Пізи з безлюдних місць на кладовищі й поставити в громадських місцях, де їх було б добре видно. Статуя Леонардо була поміщена в південній частині Понте ді Меццо. Під час Другої світової війни, у 1944 році, місто було зруйноване у битві за Пізу, а статуя потрапила на склад. У 1950 вона була знову відновлена і тимчасово розміщена у парку Джардіно Скотто біля східного входу до старого міста. Тільки в 1990-х адміністрація Пізи прийняла рішення відновити статую і помістити її назад на своє колишнє місце в Кампо-Санто.

Пам'ять

Іменем Фібоначчі названо астероїд 6765 Фібоначчі.

o       Принцип, закладений у процедурі отримання послідовності Фібоначчі, широко використовується в математиці й програмуванні. Дивіться, наприклад, статтю Купа Фібоначчі.

o       У матемаці відома тотожність Брамагупти — Фібоначчі, яку отримав індійський математик Брамагупта, і описав у «Книзі квадратів» Леонардо Пізанський.

o       Фібоначчі познайомив Європу із позиційною системою числення, однак існує система числення Фібоначчі, в основі якої лежить послідовність Фібоначчі.

«Liber abaci»

Батько мій, родом з Пізи, служив Сіндіка на митниці в Бужи, в Африці, куди він мене взяв з собою для вивчення мистецтва вважати. Дивовижне мистецтво вважати за допомогою тільки дев'яти індуських знаків мені так сподобалося, що я неодмінно захотів познайомитися з тим, що відомо про це мистецтво у Єгипті, Греції, Сирії, Сицилії і Провансі. Об'їхавши всі ці країни, я переконався, що індуська система числення є найдосконаліша ... Вивчивши грунтовно цю систему і всі до неї відноситься, додавши свої власні дослідження та почерпнуте з «Начал» Евкліда, я вирішив написати цей твір.

З передмови автора до трактату «Liber abaci»

Книга-енциклопедія

У 1202 р. з'явилася на світ знаменита «Книга абака» Леонардо Пізанського (більш відомого під прізвиськом Фібоначчі - син Боначчі), найбільшого європейського математика епохи Середньовіччя. Цей об'ємна праця, що нараховує в друкованому варіанті 459 сторінок, став справжньою енциклопедією математичних знань того часу і зіграв важливу роль у їх поширенні в країнах Західної Європи в наступні кілька століть. Робота написана на латині і вважається першим твором такого роду, автор якого був християнином.

«Liber abaci», або трактат з арифметики (а саме так можна витлумачити назву, оскільки під «абаки» Леонардо розумів не лічильну дошку, а арифметику), відрізнялася повнотою охоплення і глибиною викладу. У ній докладно роз'яснювалися не тільки ази науки про числа і дії над ними, але й основи вчення про рівняннях, тобто алгебри. Крім того, в «Liber abaci» була велика кількість завдань практичного змісту, ілюстрованих різні прийоми рішення, як арифметичні - потрійне правило, правило товариства, метод помилкового положення і т.і., так і алгебраїчні, що приводять до одного або кількох рівнянь.

Саме виклад був словесним, позбавленим звичних для сучасного читача символів і формул, а рішення прикладів і завдань, що носили, як ми говоримо сьогодні, приватний характер, зводилося до опису дій, які слід було застосовувати у тій чи іншій конкретній ситуації, і нерідко супроводжувалося роз'ясненнями або корисними коментарями автора.

Книга була адресована не тільки вченим мужам, але і більш широкому колу читачів: купцям, рахівником, продавцям, чиновникам і т.д. У передмові зазначалося, що автор написав свою працю, щоб «рід латинян» не прибував більше в незнанні викладаються в ньому речей. Проте для багатьох з тих, кому призначалася «Liber abaci», книга виявилася важкувата, тому незважаючи на популярність і доопрацьоване автором видання * 1228, не отримала того широкого поширення, якого заслуговувала.

* До нас «Liber abaci» дійшла як раз у другому варіанті. Її перше друковане видання з'явилося на батьківщині математика, в Італії, в середині XIX ст. =

Зате трактат Леонардо долучив до досягнень індійських і арабських математиків європейських вчених і зробив істотний вплив на подальший розвиток алгебри та теорії чисел. «Liber abaci» була затребувана математиками епохи Відродження та Нового часу, що зуміли оцінити її по гідності, адже книга відрізнялася не тільки багатством і різноманітністю розглянутих в ній прикладів і методів, але і строгістю, доказовістю викладу.

Протягом декількох сторіч по праці Фібоначчі вчені знайомилися з двома найважливішими розділами математики - арифметикою і алгеброю і черпали з нього завдання і оригінальні методи вирішення, завдяки чому вже в XV-XVI ст. ті розійшлися по численних італійською, французькою, німецькою, англійською, а пізніше і російською рукописів, друкованим книгам і підручникам. Деякі завдання або їх аналоги можна виявити і в «Сумі арифметики» Пачіолі (1494), і в «Приємних і цікавих задач» Баше де Мізіріака (1612), і в «Арифметиці» Магницького (1703), і навіть у «Алгебрі» Ейлера (1768).

Заслуги і досягнення Леонардо Пізанського

Яке ж було утримання написаної Фібоначчі книги-енциклопедії, в якій нараховувалося цілих п'ятнадцять глав? Виявляється, в ній розглядалося досить велике коло питань:

• індуська система нумерації;
• правила дій над цілими числами;
• дробу і змішані числа;
• розкладання чисел на прості множники;
• ознаки подільності;
• вчення про ірраціональні величини;
• способи наближеного обчислення квадратних і кубічних коренів;
• властивості пропорції;
• арифметична і геометрична прогресії;
• лінійні рівняння та їх системи.

Нарешті, окрема глава була присвячена квадратних рівнянь і геометричним завданням на застосування теореми Піфагора.

Основну частину відомостей автор копітко збирав, подорожуючи різними країнами як купець, дещо почерпнув з праць Евкліда (а по суті - з спадщини античних математиків). Особливу цінність являло докладний виклад маловідомої тоді в Європі індуської (десяткового) системи числення і нових методів обчислення, які давали можливість помітно спростити всілякі розрахунки та успішно вирішувати велике коло завдань *.

* У своїй праці Леонардо згадав про різні нумерація, як відомих у нього на батьківщині, так і використовувалися в країнах Сходу, які він відвідав, і показав переваги індуської системи числення. А починався трактат так: «Дев'ять індуських знаків суть наступні: 9, 8, 7, 6, 5, 4, 3, 2, 1. За допомогою цих знаків та знака 0, який називається по-арабськи «Сітрі», можна написати який завгодно число ».

Треба сказати, окремі випадки використання цієї системи зустрічалися і раніше. Зі Сходу її привозили паломники, вчені, купці, посланці і військові. Найбільш древній європейський манускрипт, в якому згадуються вигадані індусами цифри, належить ще до кінця X ст. Однак десяткова система числення дуже повільно проникала в західні країни і отримала там широке поширення лише в епоху Відродження.

Відзначимо також, що саме завдяки Фібоначчі європейці познайомилися з загальними правилами розв'язання квадратних рівнянь, описаними в трактаті аль-Хорезмі.

Але Леонардо Пізанський був не тільки автором-упорядником енциклопедії «Liber abaci». У ній математик відбив і результати власних наукових пошуків. Зокрема, в цій праці він вперше:

сформулював правило для знаходження суми членів довільної арифметичної прогресії;

розглянув поворотну послідовність, в якій кожне число, починаючи з третього, дорівнює сумі двох попередніх йому чисел;

ввів термін «приватне» для позначення результату ділення;

описав спосіб приведення дробів до спільного знаменника з допомогою знаходження найменшого спільного кратного знаменників (більш раціональний, ніж використовували арабські математики).

Крім того, Фібоначчі самостійно розробив ряд алгебраїчних прийомів вирішення завдань, досліджував деякі рівняння вищих ступенів, що зводяться до квадратних, і першим серед європейських учених підійшов до введення від'ємних чисел і їх тлумачення як боргу, що на ті часи було величезним досягненням.

Універсальний задачник

Чималу цінність «Liber abaci» надавало наявність в ній безлічі різноманітних завдань, одні з яких були запозичені з арабських та інших джерел, а інші придумані самим автором. Велику групу становили чисто арифметичні й алгебраїчні приклади: на виконання дій над числами, витяг коренів, рішення рівнянь або систем і т.д. В іншу групу входили сюжетні завдання (у тому числі пов'язані з життєвими ситуаціями): на змішання, визначення вартості або кількості купленого товару, розділ майна і різного роду фінансові розрахунки між людьми (завдання комерційної арифметики) і т.п.

Наприклад, до завдань на змішання ставилися два види завдань «на сплави»: на визначення проби сплаву, зробленого з інших сплавів відомого складу і кількості, і на з'ясування того, що кожного з даних сплаву буде потрібно, щоб одержати сплав потрібної проби. А однією з типових завдань комерційної арифметики було завдання на розділ деякої суми грошей пропорційно часткам учасників.

У трактат Фібоначчі ввійшли також текстові задачі на відтворення певної дії, наприклад знаходження числа за його частини. Ось одна з них. Четверта і третя частини дерева знаходяться під землею і складають 21 фут. Чому дорівнює довжина всього дерева?

Деякі з порушених у праці Леонардо питань в різний час привертали увагу вчених-математиків і не раз згадувалися в більш пізніх творах. Так сталося, зокрема, з популярною в середні століття завданням на відшукання найменшого набору різних гир, за допомогою якого можна врівноважити будь-який вантаж з целочисленной масою, не перевершує заданого числа.

Але найбільш відомою донині залишається, звичайно ж, завдання про розмноження кроликів, що вперше з'явилася саме в «Liber abaci». Питається, скільки пар кроликів народиться за рік від однієї пари, якщо кролики починають приносити потомство з другого місяця і кожна пара через місяць проводить на світ ще одну пару? Її рішення призвело Фібоначчі до відкриття чи ні самої знаменитої числової послідовності

1, 1, 2, 3, 5, 8, 13, ... ,

названої згодом його ім'ям і породила безліч досліджень, особливо пов'язаних з вивченням властивостей золотої пропорції.

Знайомі завдання з трактату Фібоначчі

А тепер поговоримо детальніше про деякі арифметичних і алгебраїчних задачах з «Liber abaci», з якими повинні легко впоратися (на відміну від перших читачів книги Леонардо) і нинішні школярі. Завдання ці цікаві не тільки, а іноді і не стільки своїми рішеннями або конкретним математичним змістом. Багато в чому вони цікаві з історичної точки зору, оскільки мають свою біографію, витримали випробування часом, «прижилися» і благополучно дійшли до наших днів. До того ж, розглядаючи запропоновану кимось завдання, ніколи не буває зайве ознайомитися з чужим міркуванням і порівняти його з власним рішенням. Тим більше, коли читача і автора поділяють сторіччя, а то і тисячоліття!

Випередив час

Як відзначають дослідники, «Liber abaci» не просто виділяється, а різко піднімається над середньовічної літературою з арифметики і алгебри. Перш за все завдяки фундаментальності викладу і різноманіттю розглянутих у ній методів і завдань. Рівень твори виявився настільки високий, що осилити і скористатися викладеними в ньому відомостями змогли головним чином вчені-математики, почасти сучасники Леонардо, і в ще великою мірою - представники наступних поколінь.

Фактично лише через три століття після виходу в світ «Liber abaci» стало помітно її вплив на роботи інших авторів. З появою праці Фібоначчі європейські вчені епохи Середньовіччя, колишні часто філософами-схоластами чи духовними особами, для кого математика не була основним заняттям, стали приділяти більше уваги алгебри та торкатися у своїх дослідженнях її нові питання. Однак перших серйозних результатів вдалося досягти тільки в епоху Відродження, до початку XVI століття, коли група італійських математиків (Сципіон дель Ферро, Нікколо Тарталья, Ієронім Кардано, Людовіко Феррарі) отримала загальне рішення кубічних рівнянь, поклавши тим самим початок вищої алгебри.

Виходить, що як учений Леонардо Пізанський не тільки перевершив, але і на багато десятиліть випередив західноєвропейських математиків свого часу. Подібно Піфагору, котрий привніс у грецьку науку знання, колись отримані від єгипетських і вавілонських жерців, Фібоначчі багато в чому сприяв передачі придбаних ним у молодості математичних знань індусів і арабів в західноєвропейську науку і заклав фундамент для її подальшого розвитку.

 

3. РОЗВ'ЯЗУВАННЯ ЗАДАЧ 

Сьогодні пропоную розв'язати задачі з, як говорять універсального збірника задач усіх часів - з книги «Книга Абака»

Завдання 1. Знайти число, 19/20 якого рівні квадрату самого числа.

Відповідь: 19/20.

Коментар. Відповідь очевидна кожному, хто знайомий з поняттям квадрата числа. Вирішуючи завдання за допомогою квадратного рівняння 19/20 x = x2 ми отримаємо ще одне задовольняє умові завдання число - 0.

Автор же, очевидно, мав на увазі число, відмінне від нуля. Що взагалі-то не дивно. За часів Леонардо Пізанського нуль не визнавався за корінь рівняння, тобто за число. Втім, це не заважало деяким математикам і до, і після Фібоначчі виконувати найпростіші операції з нулем, який сприймався ними як символ, що позначав «ніщо».

Завдання 2. Хтось помістив пару кроликів в якомусь місці, обгородженому з усіх боків стіною, щоб дізнатися, скільки пар кроликів народиться при цьому протягом року. Природа кроликів така, що через місяць пара кроликів виробляє світ іншу пару, а народжуються кролики з другого місяця. Скільки пар кроликів буде через рік?

Відповідь: 377 пар.

Коментар. Навіть однієї цієї задачі вистачило б Фібоначчі, щоб залишити слід в історії науки. Саме у зв'язку з нею сьогодні найчастіше і згадується ім'я вченого. Вирішуючи задачу про розмноження кроликів, Леонардо описав нескінченну числову послідовність (an), будь-який член якої, починаючи з третього, виражається через попередні члени:

a1 = 1, a2 = 1, an +2 = an +1 + an, де n ≥ 1.

Для математиків вона є перш за все класичним прикладом рекурентної послідовності, елементи якої, числа Фібоначчі, володіють багатьма дуже цікавими і знайшли несподівані застосування властивостями. З них широко відомо наступне: границя відношення an +1 до an при необмеженому зростанні n спрямовується до знаменитого числу Ф ≈ 1,618, виражає божественну пропорцію.

Що ж стосується відповіді в задачі про кроликів, то (відповідно до зазначених у тексті умовами) він співпадає з 13-м членом побудованої Леонардо послідовності 1, 2, 3, 5, 8, ... - Числом 377. Тут кожне число, починаючи з другого, показують, скільки всього пар кроликів буде налічуватися до початку чергового місяця.

Зауважимо, що Фібоначчі розглядав своє завдання для дорослої пари кроликів (на це вказують слова «народжуються кролики з другого місяця»). Якщо ж вирішувати її для новонародженої пари, вийде послідовність (1); в такому випадку рівно через рік кількість тварин збільшиться до 233 пар особин *.

* Через півтора століття індійський математик нарайан розглядав схожу завдання: знайти число корів та телиць, що походять від однієї корови протягом 20 років, за умови, що корова на початку кожного року приносить телицю, а телиця, досягнувши трьох років, дає таке ж потомство в початку року. Якщо вирішувати завдання, складаючи рекурентне співвідношення, прийдемо до послідовності 1, 1, 1, 2, 3, 4, 6, 9, 13, ... .

Завдання 3. Сім бабусь відправляються до Риму. У кожної по сім мулів, кожен мул несе по сім мішків, в кожному мішку по сім хлібів, в кожному хлібі по сім ножів, кожен ніж в семи піхвах. Скільки всього предметів?

Відповідь: 137 256 предметів.

Коментар. Перед нами добре відома, що зустрічається у різних народів завдання-жарт, як її часто називають історики математики, вважаючи, що в минулі часи вона була всього лише нехитрої забавою для учнів. Але ж ця висхідна ще до стародавнім єгиптянам завдання, вірніше її рішення, служить прекрасною наочною ілюстрацією побудови геометричної прогресії і знаходження суми перших n її членів за відомим перший члену і знаменника. І саме в такій якості її цілком можна використовувати у навчанні дітей математики.

Від аналогічної задачі з папірусу Рінда * завдання з трактату Фібоначчі по суті відрізняється лише тим, що в ній підсумовуються не п'ять, а шість чисел:

S6 = 7 + 72 + ... 76 = [7 · (76 - 1)] / 6 = 137256

* Нагадаємо її умова: «У семи осіб по семи кішок, кожна кішка з'їдає по семи мишей, кожна миша з'їдає по семи колосків ячменю, з кожного колоса може вирости по сім заходів зерна. Які великі числа цього ряду і як велика їх сума? »А ось для порівняння російський варіант завдання, розглянутої в книзі Леонардо:« Йшли сім старців, у кожного старця по сім милиць, на кожному милиці по сім сучків, на кожному сучку по сім Кошелев , в кожному кошіль по сім пирогів, в кожному пирозі по сім горобців. Скільки? »

Завдання 4. Вибрати п'ять гир так, щоб з їх допомогою можна було зважити будь-який вантаж масою від 1 до 30 цілих вагових одиниць. При зважуванні всі гирі дозволяється класти тільки на одну чашку ваг.

Відповідь: треба взяти гирі з масами 1, 2, 4, 8 і 16 вагових одиниць.

Коментар. Порушене у задачі питання рівносильний питання про подання натурального числа n ≤ 30 в вигляді суми не більше п'яти різних натуральних чисел з набору m1, ..., m5, що не перевершують n:

n = a1 · m1 + a2 · m2 + a3 · m3 + a4 · m4 + a5 · m5,

де кожен із множників a1, ..., a5 дорівнює 1 або 0 (гиря або кладеться на чашку ваг, або ні). Але тоді, природно перейти до двійковій системі числення:

n = a5 · 24 + a4 · 23 + a3 · 22 + a2 · 21 + a1 · 20.

Таким чином, в набір повинні входити гирі, маси яких виражаються числами 1, 2, 4, 8 і 16.

Хоча це завдання часто пов'язують з ім'ям французького математика і поета Баше де Мезіріаком *, вона зустрічається ще у Фібоначчі. Ймовірно, і той не сам її придумав. А справжнім автором цієї до недавнього часу актуальною практичного завдання міг бути який-небудь кмітливий торговець, якому частенько доводилося зважувати свій товар.

* Клод Гаспар Баше де Мезіріаком (1581 ... 1638) відомий, зокрема, як автор книг по цікавою математики. В одній з них і наведена завдання про оптимальну системі гир.

У «Liber abaci» містився також більш складний варіант розглянутої задачі. У ньому дозволяється класти гирі на обидві чашки ваг, а значить, треба буде думати не тільки про вибір гир, але і про те, куди і якій кількості їх додавати. Ясно, що в даному випадку кожне з чисел ai може приймати три різні значення (гиря додається або на вільну чашку ваг, або на чашку з вантажем або взагалі не використовується) і доводиться звертатися вже до трійкової системі числення. Вирішивши завдання для n ≤ 40, Леонардо отримав у відповіді набір гир масами 1, 3, 9 і 27 вагових одиниць.

Обидва варіанти завдання цікаві ще й тим, що знайдені числа є членами геометричних прогресій із знаменниками q = 2 і q = 3 відповідно. А до системи з п'яти гир, що згадується в задачі 4, можна прийти, розглядаючи нерівність

30 ≤ 1 + 2 + 22 + ... + 2m-1, або 30 ≤ 2m - 1.

Його найменше натуральне рішення m = 5.

Завдання 5. Якщо перша людина отримає від другого липня денаріїв, то стане в п'ять разів багатші другого, а якщо друга людина отримає від першого 5 денаріїв, то стане в сім разів багатший першого. Скільки грошей у кожного?

Відповідь: 7 2 / 17 і 9 14/17 денаріїв.

Коментар. Позначивши літерами x і y кількість грошей, наявних у першого і в другої людини, отримаємо систему

з якої знайдемо x = 7 2 / 17 і y = 9 14/17. Такий спосіб вирішення напрошується сам собою, оскільки в задачі йдеться про двох невідомих.

А ось Леонардо Пізанський у своїх міркуваннях обмежився однією невідомою, назвавши її за давно вкоріненою серед математиків традиції «річчю». Прийнявши майно другої людини за річ і сім денаріїв, тобто за (x + 7), він висловив майно першого як (5x - 7) та в подальшому прийшов до лінійного рівняння

x + 12 = 7 (5x - 12).

Принагідно зауважимо, що в трактаті Фібоначчі містяться аналогічні завдання і з більшим числом людей.

Завдання 6. 30 птахів коштують 30 монет. Куріпки стоять по 3 монети, голуби по 2, а пара горобців - по монеті. Скільки птахів кожного виду?

Відповідь: 3 куріпки, 5 голубів, 22 горобця.

Коментар. З-за великої кількості невідомих це завдання цілком логічно вирішувати алгебраїчно. Якщо число куріпок, голубів і горобців позначити буквами x, y, z відповідно, то рішення зведеться до знаходження трійки натуральних чисел, які відповідають системі рівнянь

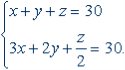
Виключивши z і висловивши потім x через y, отримаємо x = 6 - 3 / 5 y. Єдине можливе значення y дорівнює 5, тоді x = 3, z = 22.

Цікаво, що це завдання автор «Liber abaci» розглядав як завдання на сплав гідності 1, який повинен вийти з трьох цілочисельних кількостей гідністю 3, 2 і 1 / 2. Це ж завдання, але з трохи зміненими числовими даними (вартість птиці різного виду виражається зворотними числами: 1 / 3, 1 / 2 і 2) розбиралася ще в одному творі Леонардо.

Завдання 7. Вирішити систему рівнянь

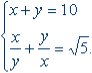
Відповідь: (15 - 5 √ 5; 5 √ 5 - 5).

Коментар. Насправді дана система є симетричною і має ні одне, як зазначив Фібоначчі, а два рішення, друге - (5 √ 5 - 5, 15 - 5 √ 5).

Але цікава завдання не тільки цим. У «Liber abaci» наведені різні способи її вирішення.

По-перше, «стандартний» в нашому розумінні: з допомогою підстановки y = 10 - x. Виключаємо y і зводимо задачу до вирішення квадратного рівняння

x2 + 100 √ 5 - 200 = 10x.

По-друге, за допомогою заміни. Нехай y / x = z, тоді x / y = √ 5 - z. Так як y / x · x / y = 1, приходимо до рівняння z (√ 5 - z) = 1, з якого визначаємо z. З іншого боку, y = 10 - x, z = (10 - x) / x, звідки легко знайти x, а потім вже обчислити y.

Ідея першого способу розв'язання виглядає, звичайно, прозоріше і звичніше, однак вирішувати їм систему технічно не простіше, ніж другим способом. А, як відомо, в подібних завданнях простота обчислень, особливо якщо ті пов'язані з корінням, грає не останню роль!

IV.            ЗАКРІПЛЕННЯ

Пропонуємо учням, щоб вони об'єналися в групи і за матеріалом уроку створили таблицю, за шаблоном:

Леонардо Пізанський                                       італ. Leonardo Pisano
Народився
Помер
Громадянство
Національність
Діяльність
Відомий завдяки (в якій галузі працював)
Володів мовами
Magnum opus
Відомий завдяки
Конфесія

Очікувана відповідь:

 

 

 

Леонардо Пізанський італ. Leonardo Pisano
Народився	близько 1170 Піза
Помер	1250 Піза
Громадянство (підданство)	Пізанська республіка
Національність	італієць
Діяльність	математик
Відомий завдяки	Математика
Володіє мовами	латина
Magnum opus	ряд Фібоначчі
Відомий завдяки:	числа Фібоначчі арабські цифри
Конфесія	християнство

 

Сьогодні ми розв'язали дуже багато задач, відповіді ми їх записали в окремий стовпчик, давайте тепер додамо всі цифри, які в нас утворилися, віднімемо від отриманого числа 1, і поділемо результат на 13. Результат Вас шокує, це оцінка кожного, хто допомагав розв'язувати ці давні задачі. (12 балів, отримає кожен учень).

1 задача	2 задача	3 задача	4 задача	5 задача	6 задача	7 задача	Сума	-1	/13	Ваша оцінка
-	-	-	-	-	-	-	157	156	12	12

 

5. ПІДВЕДЕННЯ ПІДСУМКІВ УРОКУ

Слово вчителя: Сьогодні у нас був дуже змістовний урок, з великою кількість практичних задач і я пропоную Вам відповісти на декілька питань

• Що ви дізналися сьогодні на уроці?
• Про якого великого математика ви сьгодні дізналися на уроці
• Чому він став таким відомим
• Узагальніть одну із сьогодні розв’язаних задач, і запишіть її розв’язок
• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.

 

*Для оцінювання уроку:

VI.            ДОМАШНЯ РОБОТА

Домашнє завдання сьогодні в нас буде незвичним, ви вдома, ще розв'яжете задачі з «Книги абака» , і з головою погрузетеся в середньовічну математику:

    Задачі про гирі

Завдання про вибір найкращої системи гирь для зважування на важільних терезах[10][11] вперше була сформульована саме Фібоначчі. Леонардо Пізанский пропонує два варіанти завдання:

Простий варіант: потрібно знайти п'ять гирь, за допомогою яких можна знайти вагу меншу ніж 30, при цьому гирі можна класти лише на одну чашу терезів Розв'язок будується в двійковій системі числення.

Складний варіант: потрібно знайти найменше число гирь, за допомогою якого можна зважити вагу меншу від заданої. Розв'язок будується в системі числення з основою три

    Задача про птахів і вежі

Дві пташки одночасно злітають з вершин двох веж, що знаходяться на відстані 60 метрів. Висота однієї вежі становить 50 метрів, а другої 40 метрів. При польоті з однаковою швидкістю пташки долітають одночасно до фонтану, що розташований на лінії, проведеній через дві вежі (на рівні поверхні ґрунту). На якій відстані від основи веж знаходиться фонтан?

    Задача про купця з Пізи

Пізанський купець під час торговельної подорожі до Венеції подвоїв там свій стартовий капітал, а за тим витратив 12 динарів. Потім подався до Флоренції, де знову подвоїв число своїх динарів і витратив 12. Після повернення до Пізи черговий раз подвоїв свій статок, витратив 12 динарів і ... залишився без копійки. Скільки динарів він мав на початку?

    Задача про трьох чоловіків і знайдений гаманець

Три чоловіки знайшли гаманець із 23 динарами. Перший каже другому: «Якщо я додам ці гроші до своїх, то буду мати суму, що буде у два рази більшою від тієї, що є у тебе». Другий аналогічно звернувся до третього: «Якщо я зараз візьму ці гроші собі, буду мати суму у три рази більшу від твоєї». На кінець третій каже до першого: «Якщо я додам ці гроші до своїх, то буду мати суму у чотири рази більшу, ніж у тебе». Скільки динарів мав кожен з них?

    Загадка пана з Палермо

Три придворних слуги мали свою частку в певній сумі грошей у касі: доля першого становила половину, другого - третину, а третього - шосту частину. Кожен з учасників взяв зі спільної каси гроші не зовсім чесно так, що каса залишилась порожньою. Далі перший з них повернув половину того, що взяв, другий - третину, а третій - шосту частину. Отриману суму було розділено на три однакові частини і роздано кожному з трьох слуг. Виявилось, що кожен з них мав точно стільки, скільки йому належало. Скільки коштів було у касі спочатку, яку суму взяв кожен з учасників?

 

 

    Задача про спадщину

Чоловік, що помирав покликав своїх синів і сказав найстаршому: «Візьми одного динара з моїх статків і сьому частину від того, що залишиться». Другому сину каже: «Візьми собі два динари і сьому частину того, що залишиться». До третього: «Візьми три динари і сьому частину того, що залишиться» і так далі - кожному наступному синові записував на один динар більше від попереднього і сьому частину залишку. Після поділу статків виявилось, що всі сини отримали порівну. Скільки було синів і яким був спадок?

 

 

    Задачі з теорії чисел

    Знайти число, яке ділиться на 7 і дає в залишку одиницю при діленні на 2, 3, 4, 5 і 6;

    Знайти число, добуток якого на сім дає залишки 1, 2, 3, 4, 5 при діленні на 2, 3, 4, 5, 6, відповідно;

    Знайти квадратне число, яке при збільшенні або зменшенні на 5 давало б квадратне число.

Урок 3

Тема. Математичний запис чисел Фібоначчі. Поняття рекурсії

Мета:

• навчальна: дізнатися про способи запису послідовності Фібоначчі, дізнатися про рекурсію, та про задачі зв’язані з числами Фібоначчі.
• виховна: виховувати інтерес до вивчення математики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень зможе записати формулу запису послідовності Фібоначчі, записати вигляд програми з використанням рекрсії, записати код програми виведення чисел Фібоначчі, який базується на методі рекурсії

Тип уроку: урок засвоєння нових знань, розв’язування задач.

Матеріали та обладнання: файл презентації, стенд, файл програми для демонстрацій

 Програмне забезпечення: MS Power Point (OpenOffice Impress), PascalABC.NET, DevC++.

Хід уроку

Математика - це мистецтво називати різні речі одним і тим же ім'ям.

А. Пуанкаре

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Актуалізація опорних знань з теми «Життєвий шлях і наукові здобутки Леонарда Пізанського»
   • Учням роздаються дві картки «Правда і брехня»

ПРАВДА

БРЕХНЯ

 

Далі вчитель зачитує твердження і учні підіймають картки в слід правильності тверджень

    Фібоначчі помер в 1315. (Брехня)

    Леонардо Пізанський є автором «Книга абака» (Правда)

    Леонардо Пізанський народився в Англії (Брехня)

    Фібоначчі народився в 1170 році (Правда)

    На третій місяць (за умовою задачі про кроликів) буде 10 кроликів. (Брехня)

    Леонардо Пізанський знайшов розв’язок рівняння третього ступенння. (Правда)

    Леонардо Пізанський був християном (Правда)

• Вчений, який народився в Пізі і помер 1250 року прцював на проблемою розкладання чисел на прості множники (Правда)

    Фібоначчі володів 5 мовами (Брехня)

    Якщо число ділиться на 4, то воно завжди ділиться на 2 (Правда)

  Учні розділяються на дві групи (Бібліотекарі і «Заїдлі» математики), назва вибирається жеребкуванням

БІБЛІОТЕКАРІ 

«ЗАЇДЛІ» МАТЕМАТИКА 

Для кожної команди роздаються портрети математиків, і для першої команди наукові праці цих вчених, а для другої команди, який внесок вони внесли в математику

       ПЕРША КОМАНДА

	"Вступ до аналізу нескінченних"
	Коротка книга про числення алгебри і алмукабали
	«Арифметичні дослідження»
	«Книга квадратів»
	«Начала»
	«Про світ»

       Для другої коланди

	Способи обчислення квадратних і кубічних рівнянь
	Доведення «від супротивного»
	Теорія графів
	Основна теорема алгебри: «Алгебраїчне рівняння має стільки коренів дійсних чи комплексних, скільки одиниць у показнику його степеня»
	Вперше виділив алгебру як самостійну дисципліну
	Вивів формулу знаходження n-ого члена геометричної прогречії

*Картки перед роздачею необхідно розмішати, після роздачі, учні повині встановити відповідність, команда, яка перша ВІРНО встановила відповідність, отримує бонус +1 бал, до оцінки за урок, для кожного з її учасників.

 

3. Вивчення нового матеріалу

Опираючись на слайди презентації і нижче поданий матеріал пояснити учням тему уроку.

Рекурсія (від латинського recursio - повернення) - це такий спосіб організації обчислювального процесу, при якому процедура або функція в ході виконання складових її операторів звертається сама до себе.

Для того, щоб таке звернення не було нескінченним, в тексті підпрограми повинно бути умова, по досягненню якого подальшого звернення не відбувається. таким чином, рекурсивне звернення може включатися тільки в одну з гілок підпрограми.

У мові Паскаль немає ніяких обмежень на рекурсивні виклики підпрограм, необхідно тільки розуміти, що кожен черговий рекурсивний виклик призводить до утворення нової копії локальних об'єктів підпрограми і всі ці копії, відповідні ланцюжку активізованих і не завершених рекурсивних викликів, існують незалежно один від одного

 

Рекурсія досить широко застосовується в програмуванні, що засноване на рекурсивної природі багатьох математичних алгоритмів. А також Ви повинні знати, що будь-який рекурсивний алгоритм можна перетворити в еквівалентний ітеративний (тобто використовує циклічні конструкції).

У великих і складних програмах іноді доводиться замінювати рекурсию на ітерацію. Справа в тому, що рекурсія пов'язана з багаторазовими викликами процедур, а це дещо менш ефективно при виконанні в порівнянні з використанням циклів. Однак рекурсивні версії програм, як правило, набагато коротше і наочніше.

Доброю ілюстрацією механізму рекурсії є функція для обчислення факторіала натурального числа. Згадаймо, що факторіалом числа називається твір всіх натуральних чисел від 1 до цього числа включно:

1! = 1 0! = 1 N! = 1 * 2 * 3 *. . . * (N-2) * (N-1) * N

Спочатку покажемо зазвичай не рекурсивную функцію для обчислення факторіала, яка реалізує ітеративний алгоритм обчислення:

Function NonRecFact (N: integer): LongInt;

Var

i: integer; {Змінна циклу}

Res: LongInt; {Результат}

Begin

Res: = 1;

for i: = 1 to N do

res: = Res * i;

NonResFact: = Res;

End;

Друга функція використовує рекурсивні звернення, що робить її набагато компактніше, і заснована на очевидному співвідношенні:

N! = (N-1)! * N

Іншими словами, щоб отримати значення факторіала від числа N, досить помножити на N значення факторіала від попереднього числа:

Function RecFact (N: integer): LongInt;

Begin

if N <= 1

then

ResFact: = 1

else

ResFact: = N * ResFact (N-1);

End;

Повністю програма, що обчислює факторіал числа, буде виглядати так:

*помилки запропонувати виправити учням самостійно

Program Rekurs;

Var

N: integer;

F: Longint;

Function RecFact (N: integer): LongInt;

Begin

if N <= 1

then

ResFact: = 1

else

ResFact: = N * ResFact (N-1);

End;

Begin

writeln ( 'Введіть число N>';

read (N);

F:  = RecFact (N);

writeln ( 'Для числа', N, 'значення факторіала одно', F);

End.

Після запуску програми на екран виводиться запит "Введіть число N>", потім з клавіатури зчитується введене значення і в вираженні F: = RecFact (N) викликається функція RecFact з параметром-значенням N. У підпрограмі-функції перевіряється умова N <= 1. Якщо воно виконується, то функції ResFact присвоюється значення 1 і на цьому виконання підпрограми завершується. Якщо умова N <= 1 не дотримується, то виконується обчислення добутку N * ResFact (N-1).

Обчислення твори носить рекурсивний характер, так як при цьому здійснюється виклик функції ResFact (N-1), значення якої обчислюється, в свою чергу, через виклик функції ResFact, параметром якої також буде функція ResFact, і т.д., до тих пір поки значення формального параметра N пропустити дорівнюватиме 1. Так як базова частина опису рекурсивної функції ResFact визначає значення ResFact для N = 1, рівним одиниці, то рекурсивні виклики функції ResFact більше не виконуються, а навпаки виконується обчислення функції ResFact для чисел, зростаючих від 1 до N, причому фу кція ResFact щоразу повертає значення, яке дорівнює добутку чергового числа на факторіал від попереднього числа. Останнє повернення результату обчислення функції ResFact присвоїть змінній F значення твори всіх чисел від 1 до N, тобто факторіал числа N.

Отже, при виконанні рекурсивної підпрограми здійснюється багаторазовий перехід від деякого поточного рівня організації алгоритму до нижнього рівня послідовно доти, поки не буде отримано тривіальне рішення поставленого завдання. У нашому прикладі рішення при N = 1 тривіально, тобто ResFact = 1. Потім здійснюється повернення на верхній рівень з послідовним обчисленням значення функції ResFact.

Завдання. Введіть текст розглянутої вище програми і запишіть файл на диск під відповідним ім'ям, а потім відкомпілюйте його. Після того, як компіляція закінчиться успішно, задайте для перегляду у вікні відладчика змінні N, F. Встановіть видимими одночасно вікна редактора з текстом програми та вікно перегляду. Виконайте програму в покроковому режимі з заходом в функцію і поспостерігайте за зміною значення змінної N при рекурсивних викликах функції ResFact.

Приклади

         Факторіал цілого невід'ємного числа n позначається n! і визначається як

=n×(n-1)! при n>0 і n!=1 при n=0

         Числа Фібоначчі визначаються за допомогою рекурсії:

перше і друге числа Фібоначчі рівні 1;

для n>2, n-і число Фібоначчі дорівнює сумі (n-1)-го і (n-2)-го чисел Фібоначчі.

         Трикутник Серпінського

Практично всі геометричні фрактали задаються у формі нескінченної рекурсії (наприклад, трикутник Серпінського).

         Задача «Ханойська вежа». Її змістовна постановка така:

В одному з буддійських монастирів ченці вже тисячу років займаються перекладанням кілець. Вони розташовані трьома пірамідами, на яких нанизані кільця різних розмірів. У початковому стані 64 кільця були нанизані на першу піраміду й упорядковані по розміру. Ченці повинні перекласти всі кільця з першої піраміди на другу, виконуючи єдину умову — кільце не можна покласти на кільце меншого розміру. При перекладанні можна використовувати всі три піраміди. Ченці перекладають одне кільце за одну секунду. Як тільки вони закінчать свою роботу, наступить кінець світу.

Рекурсивний варіант розв'язку задачі:

Потрібно застосувати рекурсивно алгоритм, переклавши n-1 кільце з першої піраміди на третю піраміду. Потім зробити очевидний хід, переклавши останнє найбільше кільце з першої піраміди на другу. Потім знову застосувати рекурсію, переклавши n-1 кільце з третьої піраміди на другу піраміду.

Рекурсія в програмуванні

У програмуванні рекурсія — виклик функції чи процедури з неї самої (звичайно з іншими значеннями вхідних параметрів) безпосередньо чи через інші функції (наприклад, функція А викликає функцію B, а функція B — функцію A). Кількість вкладених викликів функції чи процедури називається глибиною рекурсії.

Міць рекурсивного визначення об'єкта в тім, що таке кінцеве визначення здатне описувати нескінченно велике число об'єктів. За допомогою ж рекурсивної програми можливо описати нескінченне обчислення, причому без явних повторень частин програми.

Існує спеціальний тип рекурсії, називаний «хвостовою рекурсією». Інтерпретатори і компілятори функціональних мов програмування, що підтримують оптимізацію коду (вихідного та/або такого, що виконується), реалізують хвостову рекурсію в обмеженому обсязі пам'яті за допомогою ітерацій.

Варто уникати надлишкової глибини рекурсії, бо це може викликати переповнення стека викликів.

Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — у математиці числова послідовність {\displaystyle {F_{n}},}F_n задана рекурентним співвідношенням другого порядку

{\displaystyle F_{1}=1,F_{2}=1,F_{n+2}=F_{n}+F_{n+1},n=1,2,3,\ldots ,}

{\displaystyle F_{1}=1,F_{2}=1,F_{3}=2,F_{4}=3,F_{5}=5,F_{6}=8,F_{7}=13,F_{8}=21,\,}і т. д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях — комбінаторних, числових, геометричних.

Простіше кажучи, перші два члени послідовності — одиниці, а кожний наступний — сума значень двох попередніх чисел:

{\displaystyle 1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}1, 1, 2, 3, 5, 8 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597….

Часто, особливо в сучасному вигляді, послідовність доповнюється ще одним початковим членом:

0, {\displaystyle 1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}1, 1, 2, 3, 5, 8 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597….{\displaystyle 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}000

За визначенням, перші два числа в послідовності Фібоначчі є або 1 і 1, або 0 і 1, залежно від обраного початку послідовностей, а кожне наступне число є сумою двох попередніх.

В математичних термінах послідовність чисел Фібоначчі F_n визначається як рекурентне співвідношення

{\displaystyle F_{n}=F_{n-1}+F_{n-2},}
F_n= F_n-1+ F_n-2

и F₁= F₂=1.

із початковими значеннями

F₁=1 i F₂=1

{\displaystyle F_{1}=1,\;F_{2}=1}абo

F₁=0 i F₂=1{\displaystyle F_{0}=0,\;F_{1}=1.}

Послідовність названа на честь математика XIII століття Леонардо Фібоначчі з Пізи. Його 1202 книга Книга абака представила цю послідовність спільноті західноєвропейських математиків,^[5], хоча така послідовність вже була описана раніше як числа Вараханка в індійській математиці. Послідовність описана в Книзі абака починалася із F₁ = 1.

Дуже часто рекурсию в програмуванні показують на прикладі обчислення чисел Фібоначчі рекурсивним алгоритмом. Такий алгоритм досить простий, але час виконання зростає по експаненте при збільшенні n. Тому алгоритм працює повільно при великих n, а також може статися переповнення стека (Stack Overflow).

 

Для вирішення створимо функцію f (n), в якості аргументу вона буде отримувати число n. Ця функція буде повертати число, яке дорівнюватиме f (n-1) + f (n-2). Тобто вона викликає себе 2 рази з самої себе.

1	unsigned long long int f (int n)
2	{
3
4	return f (n-1) + f (n-2);
5	}
6
7	unsigned long long int f (int n)
8	{
9
10	return f (n-1) + f (n-2);
11	}

 

 

 

 

 

 

 

Тепер додамо возвращемое значення для f (0), f (1), f (2), щоб при виконанні функції з такими агрумент функція припиняла викликати себе і видавала значення. Для f (0) повертається значення буде 0. Для f (1) і f (2) - 1.

1	unsigned long long int f (int n)
2	{
3	if (n == 0) return 0;
4	if (n == 1 || n == 2) return 1;
5
6	return f (n-1) + f (n-2);
7	}
8	unsigned long long int f (int n)
9	{
10	if (n == 0) return 0;
11	if (n == 1 || n == 2) return 1;
12
13	return f (n-1) + f (n-2);
14	}

Зверніть увагу, функція повертає значення з типом unsigned long long int. Це дозволить їй виводити величезні числа (від 0 до 18 446 744 073 709 551 615), а значить вона зможе працювати з великими n.

Таким чином дана функція обчислює n-е число з ряду чисел Фіббоначі. Функція працює тільки з n> = 0.

В ході роботи функція викликає сама себе, розкладається, поки не викличе f (1) або f (2), які тут же повернуть 1 і не будуть робити більше нічого. Після цього функція назад «складається».

Для прикладу напишемо програму з викликом функції f () з аргументом 5 і виведемо результат.

1	#include <iostream>
2
3	using namespace std;
4
5	unsigned long long int f (int n)
7	{
6	if (n == 0) return 0;
8	if (n == 1 || n == 2) return 1;
9
10	return f (n-1) + f (n-2);
11	}
12
13	int main ()
14	{
15	cout << f (5) << endl;
16	return 0;
17	}
18	#include <iostream>
19
20	using namespace std;
21
22	unsigned long long int f (int n)
23	{
24	if (n == 0) return 0;
25	if (n == 1 || n == 2) return 1;
26
27	return f (n-1) + f (n-2);
28	}
29
30	int main ()
31	{
32	cout << f (5) << endl;
33	return 0;
34	}

Результат виконання програми

Обчислене число Фібоначчі

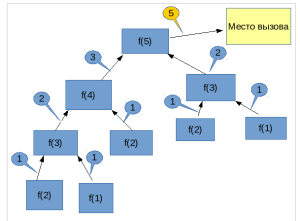Під капотом все відбувалося приблизно так: функція f (5) викликала 2 функції f (4) і f (3); функція f (4) викликала функції f (3) і f (2), а функція f (3) викликала функції f (2) і f (1) і так далі ... Але, для наочності подивіться на малюнок.

Виклики функції f ()

Стрілочка, що виходить з прямокутника з функцією, показує значення, що повертається.

МАТЕМАТИЧНІ ЖАРТИ

Математики теж люди, і у вільний час, як і ми математики всіляко розважаються – розповідають один одному жарти. Давайте наведемо приклади гумору в якокомц вигористовується поняття рекурсії:

Гумор

Більшість всіх жартів про рекурсію стосується нескінченної рекурсії, у якій немає умови виходу:

       Відоме висловлення: Щоб зрозуміти рекурсію, потрібно спочатку зрозуміти рекурсію.

       Дуже популярний жарт про рекурсію, що нагадує словникову статтю:

рекурсія 

див. рекурсія

       Кілька розповідей Станіслава Лема присвячені можливим казусам при нескінченній рекурсії:

       Розповідь про Йона Тихого та сепульки («Зоряні щоденники Йона Тихого»), у якому герой послідовно переходить від статті про сепульки до статті про сепуляції, звідти до статті про сепулькарії, у якій знову міститься посилання до статті «сепульки».

       Розповідь про розумну машину, що мала достатній розум і лінь, щоб для рішення поставленої задачі побудувати собі подібну, і доручити рішення їй (підсумком стала нескінченна рекурсія, коли кожна нова машина будувала собі подібну і передавала завдання їй).

       Російська народна казка-пісня «У попа була собака…» виявляє приклад рекурсії:

У попа була собака, він її любив

Вона з'їла шматок м'яса, він її убив

Убив і закопав,

А на могилі написав:

«У попа була собака, він її любив

Вона з'їла шматок м'яса, він її убив

Убив і закопав,

А на могилі написав:

«У попа була собака, він її любив

Вона з'їла шматок м'яса, він її убив

Убив і закопав,

А на могилі написав:

…

(лапки цитат ніколи не закриються)

       Якщо в пошуковій системі Google ввести запит «рекурсія», то в пошуковій видачі побачите слова «Можливо, ви мали на увазі: рекурсія».

IV.            ЗАКРІПЛЕННЯ ЗНАНЬ

I.            Учень, за власним бажанням виходить до дошки на якій оформлена таблиця за шаблоном

a

b

c

d

e

f

g

h

i

k

l

m

n

o

q

Де a, b, c, d, … число, яке називає учень, а нижче записує число, яке він отримав, за формулою рекурсії чисел Фібоначчі, потім учень перевіряє вірність отриманого числа, за допомогою комп’ютерної програми

*Під час роботи за комп’ютером дотримуйтеся санітарно-гігієнічних норм

Правила поведінки в комп'ютерному класі.

Загальні поняття

 Грамотна експлуатація і дисциплінована поведінка дають повну гарантію безпеки при роботі на комп'ютері.

Комп'ютер живиться від електричної мережі напругою 220В.  Напруга, більша 36В, небезпечна для людини.

  Джерелом небезпеки в комп'ютерному класі можуть бути розетки з розбитими корпусами, проводи з пошкодженою ізоляцією, прокладені по підлозі кабелі.

Інструкція з техніки безпеки

1.  Спокійно заходь в комп'ютерний зал, не штовхайся.

2.          Сідай за постійно закріплений за тобою комп'ютер.

3.          Суворо забороняється:

           торкатися задніх стінок комп'ютера і кабелів;

           торкатися до проводів живлення і заземлення;

           торкатися екрана монітора і його задньої стінки;

           вмикати і вимикати комп'ютер без дозволу вчителя;

           класти книги, зошити на клавіатуру, „мишу" або    монітор;

          працювати з мокрими руками або в мокрому одязі.

4.          Перед роботою переконайся у відсутності видимих пошкоджень.

5.          Під час роботи:

          не допускай різких і грубих ударів по клавішах;

           у жодному разі не намагайся самостійно ремонтувати ПК;

          не вставай, коли в клас заходять відвідувачі або керівництво школи;

          не натискай клавіші на сусідньому комп'ютері;

           не залишай комп'ютер без нагляду;

           якщо зникла напруга негайно вимкни комп'ютер.

6.  Після закінчення роботи:

           коректно заверши роботу з активними програмами;

          прибери робоче місце.

 

Перед Вами 3 задачі з комбінаторики, замість числових даних буквенні змінні. Ваша задача, підстватити будь-які числові значення, і розв’язати отриману задачу, записавши відповідь і підставлені числові значення. Вірність результату перевірте за допомогою калькулятора, а значення факторіалу знайдіть за допомогою програми, створеної на сьогоднішньому уроці.

                        Скільки n-значних чисел можна записати m цифрами, крім нуля якщо кожну з цих цифр можна використовувати не більше одного разу?

№  тесту	m	n	Відповідь	m!	n!
1
2
3
…
k
K+1

                        У першості школи з шахів беруть участь q учнів. Скількома способами можуть бути розподілені призові.

№  тесту	q	Відповідь	q!
1
2
3
…

 

 

•                      У пасажирському поїзді L вагонів. Скількома способами можна розсадити у поїзді F людини при умові, що вони повинні їхати у різних вагонах?

№  тесту	L	F	Відповідь	L!	F!
1
2
3
…
k
K+1

 

• Повторимо на прикладі наступних задач, як доводити задачі за допомогою методу математичної індукції

Метод математичної індукцції

1. Початок індукції: перевіряється,чи твердження, яке розглядається, виконується при n=1;
2. Індуктивний перехід: доводиться, що коли задане твердження виконується для n, то воно виконується і для n+1.

Таким чином, почавши з n=1, ми на основі доведеного індуктивного переходу одержуємо справедливість сформульованого твердження для n=2,3,…, тобто для будь-якого натурального n.

 

• Доведіть, за допомогою метода математичної індукції, що ріст чисел Фібоначчі експоненціальний, тобто

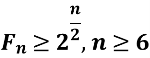
• Доведіть, за допомогою метода математичної індукції, що сума всіх n-чисел Фібоначчі, дорівнює різницю чисел- n+2 член послідовності Фібоначчі і 1, тобто

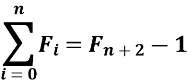
• Доведіть, що остання цифра n-ого числа Фібоначчі, дорівнює сумі остнаньої цифри n-1 члена Фібоначчі, і  останьої цифри n-2 числа Фібоначчі.
• Доведіть рівність:       F_n + ₁F_{n - 1} - F_n2 = (- 1) ⁿ        (n> 0).

Чи буде тотожність Кассіні справедливо для всіх цілих n?

Сьогодні ми з Вами ознайомилися, з поняттям про рекурсію, і побачили, що означення рекурсії дуже часто використовують в буденості. Наведіть такі приклади. За можливості наведіть малюнки.

       

***ПОРОЗМІРКОВУЙТЕ

         Чому програма, для виведення чисел Фібоначчі, яка використовує рекурсію, виконується з таким великим часом. (Свої припущення докажіть)

ОБ’ЄДНАЙТЕСЯ В ГРУПИ

Кожна група отримує таблицю, для характеристики програмного коду для програми виведення чисел Фібоначчі.

ХОРОШЕ
ПОГАНЕ
ЗЛЕ

Де хороше – це плюси і корисність коду, чому його потрібно використовувати саме в цьому випадку. Погане – мінуси даного програмного коду, чому його не бажано використовувати в даному випадку. Зле – причини складності реалізації даної математичної моделі в програному коді.

Очікувана відповідь:

ХОРОШЕ	Дуже проста реалізація, що повторює математичне визначення
ПОГАНЕ	Експоненціальне час виконання. Для великих n дуже повільно
ЗЛЕ	переповнення стека

* Команда, яка перша ВІРНО заповнила табличку і презентувала її, отримує бонус +1 бал, до оцінки за урок, для кожного з її учасників.

 

5. ПІДВЕДЕННЯ ПІДСУМКІВ УРОКУ

Підрахуйте бали, отриманні за сьогоднішній урок, якщо у вас вийшло 13 балів, то залиште отриманий сьогодні бонус на наступний урок.

Слово вчителя: Сьогодні у нас був дуже змістовний урок, з великою кількість практичних задач і я пропоную Вам відповісти на декілька питань

• Що ви дізналися сьогодні на уроці?
• Про, який спосіб виклику процедури ви сьогодні дізналися
• Про яку нову послідовність чисел ви дізналися
• Узагальніть одну із сьогодні розв’язаних задач, і запишіть її розв’язок
• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.

 

*Для оцінювання уроку:

 

6. ДОМАШНЯ РОБОТА

Сьогодні Ваше домашнє завдання буде складатись з двох видів завдань:

1. Програмування;
2. Розв’язування математичних задач.

• ЗАВДАННЯ З ПРОГРАМУВАННЯ

• Вивести на екран n перших чисел ряду Фібоначчі.
• Вивести на екран n-ий елемент ряду Фібоначчі.
• Вивести на екран n1-ий і n2-ой елементи ряду Фібоначчі і їх суму.
• Знайти двадцяте число Фібоначчі.
• Знайти подвоєне двадцяте число Фібоначчі.
• 10 випадкових чисел генеруються комп'ютером в інтервалі [5,10]. Вивести на екран числа ряду Фібоначчі. Знайти їх середнє арифметичне.
• Число x вводиться з клавіатури. Перевірити, чи є воно числом ряду Фібоначчі. Програма з тестуванням.
• Знайти кількість чисел Фібоначчі в інтервалі [2, 6].
• Знайти кількість чисел Фібоначчі в інтервалі [a, b].

• ЗАВДАННЯ З МАТЕМАТИКИ

• Знайдіть кількість слів довжини 10, що складаються тільки з букв "а" і "б" і не містять в записі двох букв "б" поспіль.
• а) Льоша піднімається по сходах з 10 сходинок. За один раз він стрибає вгору або на одну сходинку, або на дві сходинки. Скількома способами Льоша може піднятися по сходах?

б) При спуску з тієї ж сходи Льоша перестрибує через деякі сходинки (може навіть через всі 10). Скількома способами він може спуститися по цих сходах?

• Розглянемо безліч послідовностей довжини n, що складаються з 0 і 1, в яких не буває двох 1 стоять поруч. Доведіть, що кількість таких послідовностей одно F_n + 2.

Урок 4

Тема.  Формула Біне та інші способи запису чисел Фібоначчі, властивості чисел   Фібоначчі. Період Пізано

Мета:

• навчальна: дізнатися ще про способи запису послідовності Фібоначчі, реалізацію іх на мові Python3, дізнатися та про задачі інші задаі зв’язані з числами Фібоначчі.
• виховна: виховувати інтерес до вивчення математики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень зможе записати формулу запису послідовності Фібоначчі, записати вигляд програми з використанням рекрсії, записати код програми виведення чисел Фібоначчі, який базується на методі рекурсії

Тип уроку: урок засвоєння нових знань, розв’язування задач.

Матеріали та обладнання: файл презентації, стенд, файл програми для демонстрацій

 Програмне забезпечення: MS Power Point (OpenOffice Impress), Python IDLE.

Хід уроку

Людина, що не знає математики, не здатна ні до яких інших наук.

 Роджер Бекон

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Актуалізація знань з теми (Числа Фібоначчі та їх стандартна модель)

Учні об’єднуються в групи, кожна група отримує тему доповіді.

Слово вчителя : в світі є дуже багато наукових конференцій, де вчені обговорюють різноманітні проблеми, найпопулярнішою з таких платформ є TED, я пропоную Вам сьогодні теж зараз створити свою тематичну маленьку наукову конференцію, заодно і згадати теми, які ми обговорювали на минулих уроках. Перед Вашою групою тема доповіді, Вам необхідно скасти план, за необхідності намалювати малюнок, який буде наочнювати слова Вашої доповіді. Часу обмаль : 5 хвилин. Потім з кожної групи виберіть доповідача, який буде виступати перед класом. Для виступу доповідача відділяються 2-3 хвилини. Та група, яка виступить найкраще, отримає бонус +1 бал, доповідач отримає +2 бали.

*Картки з темами доповідей

Рекурсія для чайників	Історія появи чисел Фібоначчі в двох словах	Програма для виведенння Fn, з використанням рекрсії. Все не так легко
Наукові здобутки Леонарда Пізанського, і взагалі чого и його поважаємо	Задачі Фібоначчі	Рівність Касінні

 

 

 

*Бонуси

 

3. Вивчення нового матеріалу

Опираючись на слайди презентації і нижче поданий матеріал пояснити учням тему уроку.

 

 

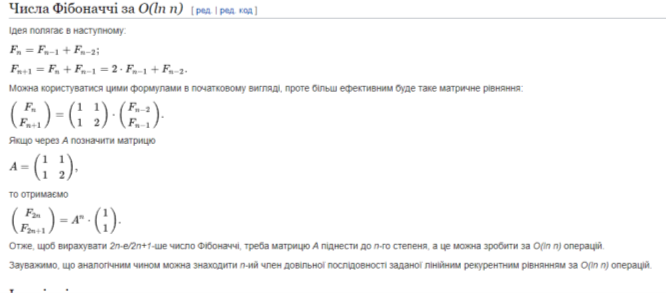
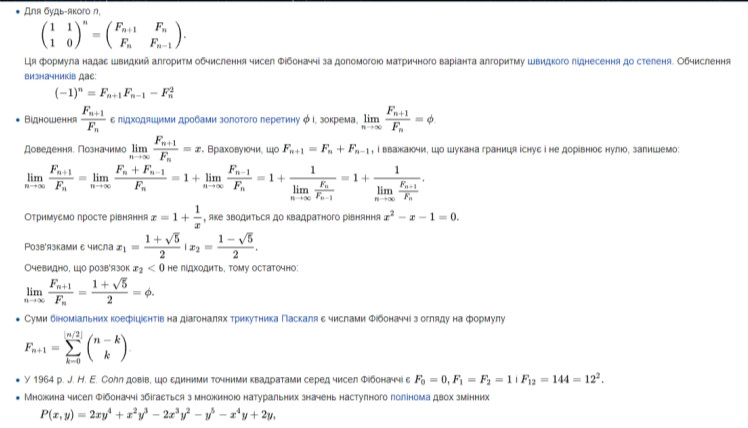
Формула Біне

     Для доведення властивостей чисел Фібоначчі використаємо формулу Біне (фр. учений  Ж. Біне 1786-1856). Яка стверджує, що будь-який член u_n послідовності чисел можна обчислити за законом, тобто

u_n = (q₁ⁿ – q₂ⁿ),                    (2)

де          q₁ = , q₂ = .     (3)

   Для доведення формули (2) можна скористатися методом математичної індукції, врахувавши специфіку означення послідовності чисел Фібоначчі. Коротко спинимося на цьому.

   Неважко переконатися, що для  n = 1, n = 2 формула (2) підтверджується.

   Припустимо, що вона має місце для номерів  n – 1, n – 2 і переконаємося в її справедливості для будь-якого номера n.

   Отже, нехай

u_n-2 = (q₁^n-1 – q₂^n-2),   u_n-1 = (q₁^n-1 – q₂^n-1).

Треба довести, що                                u_n-2 + u_n-1 = u_n = (q₁ⁿ – q₂ⁿ).

   Справді, не важко переконатися, що  1 + q₁ = q₁², 1 + q₂ = q₂², а тому u_n-2 + u_n-1 =

= [q₁^n-2 (1 + q₁) – q₂^n-2 (1 + q₂)] = (q₁ⁿ – q₂ⁿ), що й треба було довести.

Деякі (найпростіші) властивості чисел Фібоначчі

   Третій пункт плану дослідження присвячений розгляду основних властивостей чисел Фібоначчі. Сюди ми відносимо такі властивості:

1. Будь-яка пара сусідніх чисел ряду Фібоначчі u_n та u_n+1 задовольняє одне із рівнянь

х² – ху – у² = +1      (5)

    При цьому, якщо у = u_n, то х = u_n+1.

2. Сума n перших членів ряду Фібоначчі на 1 менша від (n + 2)-го члена того самого ряду:

u₁ + u₂ +…+ u_n = u_n+2 – 1.

3. Сума квадратів чисел послідовності Фібоначчі визначається через добуток двох сусідніх членів того самого ряду:

u₁² + u₂² +…+ u_n² = u_n · u_n+1.

4. Квадрат кожного члена ряду Фібоначчі, зменшений на добуток попереднього і наступного членів, дає поперемінно то +1, то -1:

u_n² – u_n-1 · u_n+1 = (- 1)ⁿ⁺¹.

5. u₁ + u₃ +…+ u_2n-1 = u_2n.
6. u₂ + u₄ +…+ u_2n = u_2n+1 – 1.
7. u_n² + u_n+1² = u_2n+1.

  Спинимося, наприклад, на доведенні першої властивості.

  Замінивши в рівнянні (5) невідомі х та у відповідними виразами (використовуючи формулу Біне)

y =(q₁ⁿ – q₂ⁿ), x = (q₁ⁿ⁺¹ – q₂ⁿ⁺¹), отримаємо:

[(q₁ⁿ⁺¹ – q₂ⁿ⁺¹)² – (q₁ⁿ⁺¹ – q₂ⁿ⁺¹)(q₁ⁿ  - q₂ⁿ) – (q₁ⁿ – q₂ⁿ)²] = ±1,

або  q₁²ⁿ⁺² – q₁ⁿ⁺¹ · q₂ⁿ⁺¹ + q₂²ⁿ⁺² – q₁²ⁿ⁺¹ + q₁ⁿ · q₂ⁿ⁺¹ + q₁ⁿ⁺¹ · q₂ⁿ – q₂²ⁿ⁺¹ – q₁²ⁿ + 2q₁ⁿ · q₂ⁿ – q₂²ⁿ = ±5.

 Групуємо члени з однаковими основами:

q₁²ⁿ · (q₁² – q₁ – 1) + q₂²ⁿ ·(q₂² – q₂ – 1) +

+ q₁ⁿ · q₂ⁿ · (-2q₁q₂ + q₂ + q₁ + 2) = ±5.

Замість q₁ і q₂ підставимо у вирази в дужках їх значення (3), дістанемо:

5a₁ⁿa₂ⁿ = ±5, або  5(a₁a₂)² = ±5.

 Але               a₁a₂ = 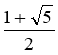· 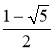= -1.

 Отже, при парному n, 5·(-1)ⁿ = 5, а при n непарному, 5·(-1)ⁿ = -5.

 Тим самим доведено першу властивість з переліку.

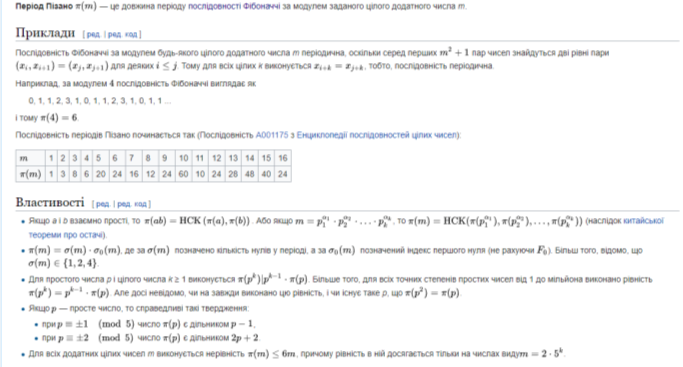
std::vector<int> pisano_periodic_sequence(int n)

{

std::vector<int> v;

int current = 0, next = 1;

v.push_back(current);

if (n < 2) return v;

current = (next += current) - current;

while (current != 0 || next != 1)

{

v.push_back(current);

current = current + next >= n ? (next += current - n) + (n - current) : (next += current) - current;

}

return v;

}

 

ЗАМКНУТА ФОРМУЛА

 

Припустимо деталі, але бажаючі можуть ознайомитися з висновком формули. Ідея в тому, щоб припустити, що є якийсь x, для якого Fn = xn, а потім знайти x.

 

 

що означає

скорочуємо xn-2

Вирішуємо квадратне рівняння:

 

 

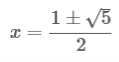
Звідки і росте «золотий перетин» φ = (1 + √5) / 2. Підставивши вихідні значення і виконавши ще обчислення, ми отримуємо:

 

 

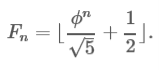
що і використовуємо для обчислення Fn.

 

from __future__ import division

import math

def fib (n):

SQRT5 = math.sqrt (5)

PHI = (SQRT5 + 1) / 2

return int (PHI ** n / SQRT5 + 0.5)

 

РЕКУРСІЯ

 

Найочевидніше рішення, яке ви вже багато разів бачили - швидше за все, в якості прикладу того, що таке рекурсія. Повторю його ще раз, для повноти. В Python її можна записати в один рядок:

fib = lambda n: fib (n - 1) + fib (n - 2) if n> 2 else 1

 

ЗАПАМ'ЯТОВУВАННЯ

 

У рішення з рекурсією є велика проблема: пересічні обчислення. Коли викликається fib (n), то підраховуються fib (n-1) і fib (n-2). Але коли вважається fib (n-1), вона знову незалежно підрахує fib (n-2) - тобто, fib (n-2) підрахувати двічі. Якщо продовжити міркування, буде видно, що fib (n-3) буде підрахована тричі, і т.д. Занадто багато перетинів.

 

M = {0: 0, 1: 1}

def fib (n):

if n in M:

return M [n]

M [n] = fib (n - 1) + fib (n - 2)

return M [n]

Тому треба просто запам'ятовувати результати, щоб не підраховувати їх знову. Час і пам'ять у цього рішення витрачаються лінійним чином. У рішенні я використовую словник, але можна було б використовувати і простий масив.

(В Python це можна також зробити за допомогою декоратора, functools.lru_cache.)

ДИНАМІЧНЕ ПРОГРАМУВАННЯ

def fib (n):

a = 0

b = 1

for __ in range (n):

a, b = b, a + b

return a

Після рішення із запам'ятовуванням стає зрозуміло, що нам потрібні не всі попередні результати, а тільки два останніх. Крім цього, замість того, щоб починати з fib (n) і йти назад, можна почати з fib (0) і йти вперед. У наступного коду лінійний час виконання, а використання пам'яті - фіксоване. На практиці швидкість рішення буде ще вище, оскільки тут відсутні рекурсивні виклики функцій і пов'язана з цим робота. І код виглядає простіше.

 

Це рішення часто наводиться як приклад динамічного програмування.

МАТРИЧНА АЛГЕБРА

 

І, нарешті, найменш висвітлене, але найбільш правильне рішення, грамотно використовує як час, так і пам'ять. Його також можна розширити на будь-яку однорідну лінійну послідовність. Ідея в використанні матриць. Досить просто бачити, що

 

 

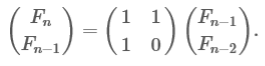
А узагальнення цього говорить про те, що

 

 

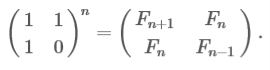
Два значення для x, отриманих нами раніше, у тому числі одне представляло собою золотий перетин, є власними значеннями матриці. Тому, ще одним способом виведення замкнутої формули є використання матричного рівняння і лінійної алгебри.

 

Так чому ж корисна таке формулювання? Тим, що зведення в ступінь можна зробити за логарифмічна час. Це робиться через зведення в квадрат. Суть в тому, що

 

 

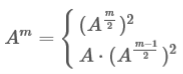
де перший вираз використовується для парних A, друге для непарних. Залишилося тільки організувати перемноження матриць, і все готово. Виходить наступний код. Я організував рекурсивную реалізацію pow, оскільки її простіше зрозуміти. Ітеративну версію дивіться тут.

 

def pow (x, n, I, mult):

"" "

Повертає x в ступені n. Припускає, що I - це одинична матриця, яка     перемножується з mult, а n - позитивне ціле

"" "

if n == 0:

return I

elif n == 1:

return x

else:

y = pow (x, n // 2, I, mult)

y = mult (y, y)

if n% 2:

y = mult (x, y)

return y

def identity_matrix (n):

"" "Повертає одиничну матрицю n на n" ""

r = list (range (n))

return [[1 if i == j else 0 for i in r] for j in r]

def matrix_multiply (A, B):

BT = list (zip (* B))

return [[sum (a * b

for a, b in zip (row_a, col_b))

for col_b in BT]

for row_a in A]

def fib (n):

F = pow ([[1, 1], [1, 0]], n, identity_matrix (2), matrix_multiply)

return F [0] [1]

 

4. РОЗВ’ЯЗАННЯ ЗАДАЧ

              Давайте розв’яжемо задачі наступної схеми, спочатку буде твердження, потім питання, яке буде опиратися на нього:

      1. Кожний третій член послідовності Фібоначчі – парне число.

Завдання:

Експериментальним шляхом перевірити дану властивість.

2. Кожний четвертий член послідовності – число, яке ділиться  на 3 без остачі.

Завдання:

Експериментальним шляхом перевірити дану властивість.

 

       3. Кожний п’ятнадцятий член послідовності – число, яке закінчується нулем.

Завдання:

Експериментальним шляхом перевірити дану властивість.

4. u₁²+u₂²+u₃²+…+u_n²= u_n u_n+1 (для будь-якого n).

 

 Експериментальним шляхом перевіимо: для n=4.

u₁²+u₂²+u₃²+ u₄²= u₄ u₄₊₁

u₁²+u₂²+u₃²+ u₄²= u₄ u₅

1²⁺1²+2²+3²=3·5

     1+1+4+9=15

                15=15.

Завдання:

Експериментальним шляхом перевірити дану властивість для n=5, n=7.

       5.    u₁+u₂+u₃+…+u_n= u_n+2 -1   (для будь-якого n).

 Експериментальним шляхом перевіимо: для n=5.

u₁+u₂+u₃+ u₄+u₅= u₅₊₂ -1

u₁+u₂+u₃+ u₄+u₅= u₇ -1

       1+1+2+3+5=13-1

                      12=12

Завдання:

       Експериментальним шляхом перевірити дану властивість для n=6, n=8.

 

       6.    u_m+k = u_k-1u_m+u_k u_m+1   (для будь-якого n).

 Експериментальним шляхом перевіимо: для m=3, k=5.

           u₃₊₅ = u_5-1u₃+u₅ u₃₊₁

              u₈ = u₄u₃+u₅ u₄

              21= 3·2 +5·3

              21=21

Завдання:

Експериментальним шляхом перевірити дану властивість для m=4, k=7.

 

• Вставте в програми розглянуті на сьогоднішньому уроці, прогрмний код який виводить кількість часу, за який виконується програма. Після зроблеої операції учні за бажанням виходять до дошки і виконує програму і заповнює таблицю.

№ тесту	Значення n	Рекурсія	Формула Біне	Динамічне програмування	Матрична алгебра	Запам’ятовування

 

• Знайдіть значення періоду Пізано для деякого n, перевірте свої припущення користуючись програмою для виведення періоду Пізано. Свої результати запишіть у таблицю

№ тесту	Значення n	Програма

 

5. ПІДВЕДЕННЯ ПІДСУМКІВ

Підрахуйте бали, отриманні за сьогоднішній урок, якщо у вас вийшло 13 балів, то залиште отриманий сьогодні бонус на наступний урок.

Слово вчителя: Сьогодні у нас був дуже змістовний урок, з великою кількість практичних задач і я пропоную Вам відповісти на декілька питань

• Що ви дізналися сьогодні на уроці?
• Про які властивості чисел Фібоначчі ви сьогодні дізналися
• Про які, ще способи виведення чисел Фібоначчі ви сьогодні дізналися
• Узагальніть одну із сьогодні розв’язаних задач, і запишіть її розв’язок
• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.

 

*Для оцінювання уроку:

 

6. ДОМАШНЯ РОБОТА

Сьогодні Ваше домашнє завдання буде складатись з двох видів завдань:

3. Програмування;
4. Розв’язування математичних задач.

 

• ЗАВДАННЯ З ПРОГРАМУВАННЯ

*завдання взяті з ресурсу EOLYMP

Неоднозначность по Фибоначчи

Как известно, в качестве базы для представления целых чисел в системе Фибоначчи взяты числа 1, 2, 3, 5, 8, 13,21, 34, 55, 89, ... . Т.е. взяты подряд все т.н. числа Фибоначчи, начиная с F(2). Запись целого числа в этой системе представыляет собой двоичную комбинацию, в которой самый младший (правый) разряд соответствует числу 1, следующий – числу 2 и т.д. Единица означает, что соответствующий член базы вносит свою лепту (равную своей величине) в величинну данного числа, а 0 означает, что соответствующий элемент базы в данную запись числа свою лепту не вносит. Например, запись (101001)_f, обозначает число 1·1+0·2+0·3+1·5+0·8+1·13=19. Легко заметить, что в отличии от стандартной двоичной системы, в системе Фибоначчи представления чисел не однозначны. Например, приведенное выше число 19 в этой же системе можно записать и так (11111)_f.

Для заданного целого числа N определить количество его различных представлений в системе Фибоначчи.

Входные данные

Число N (-10⁷ ≤ N ≤ 10⁷).

Выходные данные

Единственная строка - ответ здачи.

 

 

Числа Фибоначчи

Числа Фибоначчи задаются формулами F₁ = 1, F₂ = 1, F_i = F_{i - 1} + F_{i - 2}.

Требуется посчитать последние k цифр n-го числа Фибоначчи.

Входные данные

В первой строке входного файла содержится натуральное число n. n ≤ 10¹⁸, k = 3.

Выходные данные

Первая строка выходного файла должна содержать единственное число - ответ на задачу.

 

 

А чем Миша хуже Васи и Даши?

Миша где-то вычитал, что такое цифровой корень числа: "Если мы сложим все цифры какого-либо числа, затем все цифры найденной суммы и будем повторять это много раз, мы, наконец, получим однозначное число (цифру), называемое цифровым корнем данного числа. Например, цифровой корень числа 34697 равен 2 (3+4+6+9+7=29; 2+9=11; 1 + 1=2)."

Миша ввёл своё понятие: цифровой корень 4-го порядка - это описанный выше цифровой корень, но находится он по последним 4-м цифрам числа. Поэтому цифровой корень 4-го порядка для числа из примера выше равен 8.

Помогите Мише найти цифровой корень 4-го порядка k-го числа Фибоначчи.

Напомним, что числа Фибоначчи определяются следующими рекуррентными соотношениями:

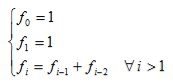
Входные данные

В каждой строке входного файла задано единственное число k (0 ≤ k ≤ 9223372036854775807).

Выходные данные

Для каждого примера входных данных выведите в отдельной строке единственное число - ответ на поставленную задачу

 

• ЗАВДАННЯ З МАТЕМАТИКИ

• Сколько существует последовательностей из 1 и 2, таких что сумма чисел в каждой такой последовательности равна n? Например, если n = 4, то таких последовательностей пять:

1111,    112,    121,    211,    22.

• О том, как прыгают кузнечики. Предположим, что имеется лента, разбитая на клетки и уходящая вправо до бесконечности. На первой клетке этой ленты сидит кузнечик. Из любой клетки кузнечик может перепрыгнуть либо на одну, либо на две клетки вправо. Сколькими способами кузнечик может добраться до n-ой от начала ленты клетки? 
• Некоторый алфавит состоит из 6 букв, которые для передачи по телеграфу кодированы так:

^.          -          ^{. .}          - -          ^. -          -   ^.

При передаче одного слова не сделали промежутков, отделяющих букву от буквы, так что получилась сплошная цепочка из точек и тире, содержащая 12 знаков. Сколькими способами можно прочитать переданное слово? 
 

 

 

 

 

Урок 4

Тема.  Розв’язування задач олімпіадного програмування, які опираються на властивості чисел Фібоначчі

Мета:

• навчальна: навчитися розв’язувати задачі олімпіадного програмування, які використовують числа фібоначчі
• виховна: виховувати інтерес до вивчення математики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень зможе розв'язувати задачі які використовують числа Фібоначчі

Тип уроку: розв’язування задач.

Матеріали та обладнання: файл презентації, стенд

 Програмне забезпечення: MS Power Point (OpenOffice Impress), Python IDLE (або інші програми для розв’язування прикладних задач).

Хід уроку

Математика - цариця наук, арифметика - цариця математики.

К.Ф. Гаусс

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Актуалізація знань з теми (Етапи розв’язання задач за допомогою комп’ютера)

Учні об'єднуються в групи, кожна з яких розповідає про етапи розв'язання задач за допомогою комп'ютера, та наводить приклад задачі та етапи її розв'язку

.

Та група, яка виступить найкраще, отримає бонус +1 бал, доповідач отримає +2 бали.

*Бонуси

 

Очікувана відповідь:

Етапи розв’язування задач за допомогою комп’ютера

Для успішного розв’язку будь-якої задачі потрібно чітко визначити послідовність дій. Як це саме зробити - якраз цьому і присвячена ця стаття.

З самого початку комп’ютери були створені для арифметичних обчислень і власне кажучи вони тільки те і вміли, що швидко виконували обчислення. Сьогодні комп’ютери використовуються для вивчення явищ природи, управління технологічними процесами, в кіно, телебаченні, у видавництві тощо. І ми зараз розглянемо, як можна використати комп’ютер для розв’язання різних і не тільки розрахункових задач, а також розглянемо основні етапи розв’язання задачі за допомогою комп’ютера.

 

Розв’язання задач в будь-якій сфері діяльності – це завжди отримання деяких результатів. А процес отримання результатів спирається на деякий спосіб дій і пропонує використання визначених засобів. Одним із нових засобів розв’язання різних задач стають сучасні комп’ютери – універсальні пристрої опрацювання і накопичування даних.

Універсальність комп’ютерів полягає в тому, що вони можуть опрацьовувати будь-які дані і розв’язувати задачі в будь-якій предметній області.

Розв’язання задачі на комп’ютері проходить в декілька етапів.

1-й етап – постановка задачі. На цьому етапі будується описова інформаційна модель об’єкта чи процесу. Пошук розв’язання будь-якої задачі розпочинається з аналізу її умови. Результатом аналізу повинна стати чітка постановка задачі, в якій повинно бути відповіді на чотири запитання:

Що дано?

Що потрібно?

Які дані допустимі?

Які результати будуть правильними, а які ні?

Розглянемо процесс розв’язування задачі на конкретному прикладі:

Спочатку формулюється умова задачі звичайною мовою.

Потім дається точна постановка задач.

Далі слідує саме розв’язок задачі.

Задача.

Тіло кинуто із швидкістю 100 м/с під кутом a до  горизонту. Визначити його положення в будь-який момент часу.

Постановка задачі.

Дано:

V=100 м/с – початкова швидкість,

a- кут кидання ( в градусах),

t – час польоту (с).

Потрібно:

x, y – координати тіла (м)

при о<a<90^o, t>0.

2 -й етап – розробка математичної моделі.  Математична модель – це математичні відношення, які зв’язують результати з вихідними даними.

Правильність результатів розв’язування задачі за допомогою комп’ютера залежить, перш за все, від правильності вибраного методу розв’язку. Метод розв’язку є правильним, якщо для будь-яких допустимих вихідних даних він приводить до результату, які відповідають постановці задачі. Для розв’язування задач за допомогою комп’ютера відповідним методам потрібно дати математичну інтерпретацію. Як правило, будується математична модель задачі. Створюючи математичну модель, потрібно записувати  математичні  відношення (формули, рівняння, нерівності тощо), які зв’язують результати з вихідними даними. Якщо повернутися до попередньої задачі, то математична модель для цієї задачі можна записати так:

 

 

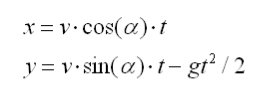
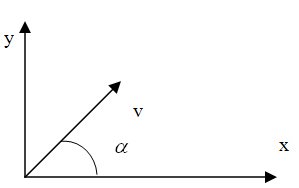
3- й етап – конструювання. На основі математичної моделі конструюється алгоритм. Про поняття алгоритму і його властивостях і способи конструювання ми будемо вивчати на  наступних уроках. А тут даний етап виконаємо для нашої задачі без детальних пояснень.

Алгоритм:

ввести v,a.

Якщо a<=0 і a>=0, то ВИВІД “ Недопустиме значення кута”. Перейти до п.1

Ввести t.

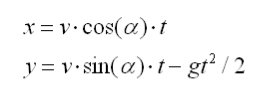
Вивід x, y.

4- й етап – перевід алгоритму в програму. Дальше дослідження інформаційної моделі, записаної у вигляді алгоритму, можна проводити різними способами. Можна закодувати алгоритм на мові програмування або використати спеціальні програмні додатки.

5- й етап розв’язування задачі полягає в проведенні комп’ютерного експерименту. Якщо ми досліджуємо інформаційну модель у вигляді програми в деякому середовищі програмування, то до цього етапу відносяться:

завантаження вибраного середовища програмування;

набір тексту програми;

збереження цього тексту на диску;

запуск програми на виконання.

Причому необхідно запускати програму на виконання декілька разів – при різних значеннях початкових умов. Можна скористатись і готовими програмними засобами. Так, наприклад, якщо інформаційна модель досліджується в електронних таблицях, то різні числові дані вводяться у відповідні комірки.

6- й етап полягає в аналізі отриманих результатів і корегуванні досліджуваної моделі. Для нашої задачі очевидно, що по-перше, доцільно отримати значення координат для послідовності моментів часу і по-друге, немає фізичного сенсу обчислення координат тіла після його падіння на поверхню землі.

Приклад 1.1 Задача. Знайти, скільки потрібно квадратних плиток зі стороною 15 см, щоб застелити підлогу ванної кімнати, розміри якої 3,3 м на 2,8 м.

Побудуємо математичну модель задачі: плитка має форму квадрата, підлога форму прямокутника. Завдання, що поставлене у задачі, мовою математики формулюється так: у скільки разів площа прямокутника зі сторонами 3,3 м і 2,8 м більші від площі квадрата зі стороною 15 см.

Розв’язання математичної задачі.

Площа прямокутника: 3,3*2,8=9,24(кв.м)

Площа квадрата: 15*15=225(кв.см)=0,0225(кв.м)

Відношення площ: 9,24/0,0225=410,6

Записуємо результат мовою вихідної задачі. Щоб застелити підлогу, потрібно не менше ніж 411 плиток.

Приклад 1.2 Задача. На реостат подали напругу 22В. Коли напругу збільшили на 10%, а опір реостата зменшили на 9Ом, то сила струму в реостаті збільшилася на 1,1 А. Знайти початковий опір реостата.

Побудуємо математичну модель задачі: Нехай початковий опір реостата x Ом, а початкова сила струму – y А. Оскільки початкова напруга 22 В, 22=yx(U=IR- закон Ома для ділянки кола). Коли напруга стала 22*1.1=24.2 В (збільшилась на 10%), опір став

(х-9) Ом, то сила струму стала (y+1,1) А. маємо: 24,2=(y+1,1)(х-9).

Математичною моделлю є система рівнянь:

x*y=22;

(x-9)*(y+1,1)=24,2

 

 

3. Розв'язання задач

 

Fibonacci haters` nim 2. Peter strikes back!

Даная задача содержит зашкаливающее количество НЕНАВИСТИ. Мы настоятельно рекомендуем
убрать от мониторов людей, животных со слабой
психикой, кормящих женщин и детей.
Администрация

Мистер Хамстер ненавидит Фибоначчи. И не только самого математика, но и всё, что с ним связано. Особенно он ненавидит числа Фибоначчи. Напомним, что числа Фибоначчи задаются по следующему правилу:

f₀ = a;
f₁ = b;
f_i = f_i-1 + f_i-2, i ≥ 2

А ещё мистер Хамстер обожает играть в ним. Он даже проводит соревнования по ниму у себя в сарае. И, конечно же, он не потерпит в своём доме ход, на котором кто-то берёт число камней, равное какому-то из чисел Фибоначчи, пусть даже этот ход принесёт победу.

Сегодня мистер Хамстер решил сыграть с маленьким Петей – он разложил на столе N кучек нима и предоставил мальчику право первого хода. Но мистер Хамстер забыл, что у Пети есть супер-способность постоянно спрашивать: "А если я выберу кучки с номерами от l до rвключительно, и мы будем играть, кто победит?" Поскольку вопросов очень много, а мистер Хамстер ненавидит программирование из-за детской психологической травмы (учитель информатики заставлял его вычислять числа Фибоначчи), то отвечать на вопросы придётся вам. Спешите, а то мистер Хамстер возненавидит и вас!

Входные данные

В первой строке следуют 3 числа: a, b и N (1 ≤ a, b ≤ 20, 1 ≤ N ≤ 10⁵). Вторая строка содержит размеры кучек b_i (1 ≤ b_i ≤ 10⁶). В третьей строке находится число M (1 ≤ M ≤ 10⁵) – количество вопросов Пети. Последующие M строк содержат пары чисел l_i r_i (1 ≤ l_i ≤ r_i ≤ N) – промежуток, на котором предлагает выбрать кучки Петя во время очередного вопроса.

Выходные данные

Выведите строку из M символов, в которой i-й символ является ответом на i-й вопрос – 'P', если побеждает Петя и 'H' – в противном случае

Лимит времени 2 секунды

Лимит использования памяти 256 MiB

Входные данные

2 1 5

1 2 3 4 5

3

1 5

1 4

2 5

Выходные данные

PHP

 

Число Фибоначчи

Числа Фибоначчи определяется следующим образом:

F (1) = F (2) = 1

F (n) = F (n - 1) + F (n - 2) для n ≥ 3.

Вычислить n-тое число Фибоначчи.

Входные данные

В первой строке задано количество тестов t (1 ≤ t ≤ 10³). Каждая из следующих t строк содержит одно число n (1 ≤ n ≤ 10⁴).

 

Входные данные #1

5

1

2

3

4

5

Выходные данные #1

1

1

2

3

5

 

Выходные данные

Для каждого теста выведите в отдельной строке соответствующее число Фибоначчи.

Задача A + B

Знаете ли вы известную последовательность Фибоначчи? Она определяется рекуррентно следующим образом:

F₀ = 0, F₁ = 1 и F_n = F_n-1 + F_n-2 для n ≥ 2.

Числа Фибоначчи обладают многими интересными свойствами. Одним из них является то, что числа Фибоначчи могут быть использованы для представления целых чисел. Каждое натуральное число имеет единственное представление в виде

n = F_k1 + F_k2 + … + F_km, k_i ≥ k_{i -1} + 2 для 2 ≤ i ≤ m и k₁ ≥ 2

Например, 6 можно представить в виде F₂+F₅, а 12 может быть представлено ​​в виде F₂+F₄+F₆.

Теперь вы знаете, как представлять натуральные числа при помощи чисел Фибоначчи, но сможете ли Вы сложить их? Заданы два натуральных числа, сформированных при помощи чисел Фибоначчи. Ваша задача вычислить их сумму.

Входные данные

Первая строка содержит одно целое число T, указывающее на количество тестовых случаев.

Каждый тестовый случай состоит из двух строк, каждая строка содержит целое число m, за которым следует m целых чисел k₁, k₂, …, k_m,указывающих на способ формирования целого числа при помощи чисел Фибоначчи F_k1+F_k2+…+F_km.

Корректность входных данных гарантируется. 1 ≤ T ≤ 100, 1 ≤ m ≤ 100, 2 ≤ k_i ≤ 1000000.

Выходные данные

Для каждого тестового случая выведите сначала номер тестового случая, а затем в следующей строке укажите сумму двух заданных чисел, также сформированную, как и во входных данных, при помощи чисел Фибоначчи.

Лимит времени 1 секунда

Лимит использования памяти 64 MiB

Входные данные

2

1 2

2 2 4

3 2 4 6

2 2 5

Выходные данные

Case 1:

1 5

Case 2:

2 5 7

 

 

Период Пизано

В 1960 году Дональд Уолл из IBM, Phite Plains, Нью-Йорк, доказал, что множество чисел Фибоначчи, взятое по модулю m, является периодичным.

Рассмотрим первые десять чисел Фибоначчи, и их остатки при делении на 11:

n	|	1	2	3	4	5	6	7	8	9	10
F(n)	|	1	1	2	3	5	8	13	21	34	55
F(n) mod 11	|	1	1	2	3	5	8	2	10	1	0

Последовательность остатков повторяется. Пусть k(m) - длина повторяющейся подпоследовательности, тогда k(11) = 10.

Уолл доказал несколько свойств, некоторые из которых будут Вам интересны:

• Если m > 2, то k(m) четно.
• Для любого четного n > 2 существует такое m, что k(m) = n.
• k(m) ≤ m² - 1
• k(2ⁿ) ≤ 3 * 2^(n-1)
• k(5ⁿ) = 4 * 5ⁿ
• k(2 * 5ⁿ) = 6n
• Если n > 2, то k(10n) = 15 * 10^(n-1)

Напишите программу, которая вычислит длину повторяющейся подпоследовательности k(m) для различных значений модуля m.

Входные данные

Первая строка содержит количество тестов p (1 ≤ p ≤ 1000). Данные каждого теста расположены на одной строке и содержат два целых числа n и m, где n - номер теста, а m (2 ≤ m ≤ 1000000) - значение модуля.

Выходные данные

Для каждого теста вывести в отдельной строке номер теста n, пробел, и длину повторяющейся подпоследовательности для m - значение k(m).
Лимит времени 1 секунда

Лимит использования памяти 122.17 MiB

Входные данные #1

5

1 4

2 5

3 11

4 123456

5 987654

Выходные данные #1

1 6

2 20

3 10

4 15456

5 332808

 

Месть Фибоначчи

Последовательность чисел Фибоначчи определяется следующим образом:

Здесь n - индекс номера числа Фибоначчи F(n).

Эта последовательность хорошо была изучена с момента публикации книги Фибоначчи. С тех пор было обнаружено множество свойств указанной последовательности.

Вас заинтересовала эта последовательность после прочтения множества статей о ней. Однако Вы решили больше не заниматься ее исследованием, так как у нее больше не осталось неисследованных свойств. Вчера Вы решили изучать другие последовательности, как например последовательность Люка.

Фибоначчи пришел в Ваш сон прошлой ночью. "Глупые человеческие существа. Еще много важных свойств последовательности Фибоначчи не изучены, например начиная с номера 347746739…"

Вы проснулись, но не смогли вспомнить все число, кроме нескольких его первых чисел, которое сообщил Вам Фибоначчи. Вы решили написать программу, которая сможет найти это число. Так Вы сможете продолжить свои исследования по последовательности Фибоначчи.

Входные данные

Состоит из нескольких тестов. Первая строка содержит количество тестов t (t ≤ 50000).

Каждый тест состоит из одной строки, в которой записана непустая последовательность из не более чем 40 цифр. Ведущие нули в строках отсутствуют.

Выходные данные

Для каждого теста вывести наименьший индекс наименьшего числа Фибоначчи, десятичная запись которого начинается с заданных цифр. Если никакое число Фибоначчи с индексом меньшим чем 100000 не удовлетворяет этому условию, то вывести -1 – то что сказал Фибоначчи лежит за пределами Ваших возможностей.

Лимит времени 5 секунд

Лимит использования памяти 256 MiB

Входные данные

15	1
12	123
1234	12345
9	98
987	9876
98765	89
32	51075176167176176176
347746739	5610
Выходные данные	Case #1: 0
Case #2: 25	Case #3: 226
Case #4: 1628	Case #5: 49516
Case #6: 15	Case #7: 15
Case #8: 15	Case #9: 43764
Case #10: 49750	Case #11: 10
Case #12: 51	Case #13: -1
Case #14: 1233	Case #15:

 

4. Підведення підсумків уроку

Слово вчителя: Сьогодні у нас був дуже змістовний урок, з великою кількість практичних задач і я пропоную Вам відповісти на одне питання

• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.

 

*Для оцінювання уроку:

 

5. ДОМАШНЯ РОБОТА

____________________________________________________________________

Количество чисел Фибоначчи

Последовательность Фибоначчи - это такая последовательность, в которой каждый элемент равен сумме двух предыдущих, за исключением первых двух элементов F₁ = 1, F₂ = 1, F_n = F_n-2 + F_n-1.

1 1 2 3 5 8 13 21 …

Задан массив целых чисел, среди которых возможно есть числа Фибоначчи. Подсчитайте количество чисел Фибоначчи в заданном наборе чисел.

Входные данные

В первой строке записано число k - количество чисел, в следующей строке записано k чисел a₁, a₂, …, a_k (0 < k ≤ 1000, 1 ≤ a_i < 2⁶³).

Выходные данные

Вывести одно число - количество чисел Фибоначчи.

Лимит времени 1 секунда

Лимит использования памяти 64 MiB

Входные данные

5

1 3 5 6 13

Выходные данные

4

___________________________________________________________________

 

Строки Фибоначчи

Последовательность строк Фибоначчи определяется следующим образом: s₁ = b, s₂ = a, s_k = s_k-1 + s_k-2 для k >2. Например, s₃ = ab, s₄ = aba, s₅ = abaab и т.д.

Даны натуральные числа n, m, l. Вывести подстроку строки s_n, начинающуюся с позиции m и имеющую длину l.

Входные данные

Содержит одну строку, в которой находятся три разделённых пробелом натуральных числа n, m и l, где 1 ≤ n ≤ 40; 1 ≤ m ≤ длина(S_n), 1 ≤ l≤ 1000.

Входные данные

Вывести подстроку строки s_n, начинающуюся с позиции m и имеющую длину l (длина выведенной подстроки может оказаться меньше, если длина оставшейся части строки s_n, начинающейся с позиции m, меньше l).

Лимит времени 1 секунда

Лимит использования памяти 128 MiB

Входные данные #1

5 3 2

Выходные данные #1

aa

Входные данные #2

5 3 10

Выходные данные #2

aab

____________________________________________________________________

 

Дружні числа

Два різних натуральних числа називаються дружніми, якщо перше з них дорівнює сумі дільників другого числа, за виключенням самого другого числа,а друге дорівнює сумі дільників першого числа, за виключенням самого першого числа. Необхідно знайти всі пари дружніх чисел, обидва з яких належать проміжку від M до N. **(1

Лимит времени 0.2 секунда

Лимит использования памяти 64 MiB

Входные данные #1

200 300

Выходные данные #1

220 284

Входные данные #2

200 250

Выходные данные #2

Absent

Входные данные #3

185000 205000

Выходные данные #3

185368 203432

196724 202444

___________________________________________________________________

Новый ряд Фибоначчи

Новая последовательность Фибоначчи образована таким образом: первые четыре члены последовательности равны единице, а каждый последующий член последовательности равен сумме четырех предыдущих.

Найти N-й член новой последовательности Фибоначчи.

Входные данные

В первой сроке задано число T - количество тестовых случаев в тесту. Во последующих строках задано T чисел - индексы искомых членов новой последовательности. 1 ≤ T ≤ 1000

Выходные данные

T строк с найденными членами новой последовательности.

Количество цифр в каждом искомом числе не превышает 2008

 

Лимит времени 1 секунда

Лимит использования памяти 64 MiB

 

Входные данные

3

3 6 9

 

 

Выходные данные

1

7

49

____________________________________________________________________

 

 

 

 

 

 

 

 

Урок 6

Тема.  

Практична робота : «Аналіз алгоритмів виведення чисел Фібоначчі. Розв’язування олімпіадних задач »

Мета:

• навчальна: навчитися розв’язувати задачі олімпіадного програмування, які використовують числа фібоначчі, навчитися аналізувати алгоритми
• виховна: виховувати інтерес до вивчення математики, наполегливість у навчанні;
•  розвивальна: розвивати логічне мислення, пам'ять, структурованість та критичність мислення.

Очікуванні результати: учень зможе розв'язувати задачі які використовують числа Фібоначчі, проаналізувати алгоритми

Тип уроку: практична робота.

Матеріали та обладнання: завдання практичної роботи

 Програмне забезпечення: MS WORD, Python IDLE (або інші програми для розв’язування прикладних задач).

Хід уроку

Чиста математика - це такий предмет, де ми не знаємо, про що ми говоримо, і не знаємо, чи істинне те, що ми говоримо.

Бертран Рассел

1. Організаційний момент

Привітання учнів та перевірка готовності до уроку.

2. Розв’язування завдань практичної роботи

 

Тема: Аналіз алгоритмів виведення чисел Фібоначчі. Розв’язування олімпіадних задач

Мета: на практиці реалізувати різні способи виведення F_n , навчитися знаходити час виконання алгоритму, навчитися характеризувати алгоритми за системою: добре, погане, зле; навчитися розв’язувати задачі олімпіадного програмування.

Обладнання: ПК з операційною системою ядра Windows або Linux, на якій встановлена середа розробки Python IDLE і MS WORD.

Хід роботи

Перед виконанням практичних або проектних завдань ознайомлітся з првилами поведінки за ПК

1. Запустіть Python IDLE, створіть п’ять нових файлів: recursia.py  pamiat.py  matrik.py  fbine.py  dinamik.py  .
2. За допомогою матеріалів наведених в уроці 4, створіть п’ять різних кода програм виведення F_n

1. За допомогою рекурсії
2. За допомогою запам’ятовування
3. За допомогою матричної алгебри
4. За допомогою формули Біне
5. За допомогою динамічного прогоамування.

3. У каркас програмного коду вставте код, який буде регеструвати кількість часу роботи програми:

Вигляд:

import time

start_time=time.time

main() //

print(“ --- % s second---”%(time.time()-time_start())

4. Під час експлуатації програми створіть для кожної програми табличку, де вкажіть час виконання коду для n – 10, 17, 135.

 

 

Назва програми
Значення n	Час виконання
10
17
135

5. Під час реалізації алгоритму виберіть один із способів реалізації і заповніть таблицю за наступним шаблону

Назва програми
Значення n	Отримане значення	Час виконання	Оперативна пам'ять

6. Порівнявши тестування програм створіть таблицю за прикладом:

	Реурсія	Запам’ятовування	Формула Біне	Матрична алгебра	Динамічне програмування
Хороше
Погане
зле

Де хороше – це плюси і корисність коду, чому його потрібно використовувати саме в цьому випадку. Погане – мінуси даного програмного коду, чому його не бажано використовувати в даному випадку. Зле – причини складності реалізації даної математичної моделі в програному коді.

7. Теоретичне завдання

Доведіть, що час виконання алгоритму рекурсії, для виведення послідовності Фібоначчі росте експоненціально.

8. Розв’яжіть подані нижче задачі, створіть файли де збережіть їхні розв’язки.

Тест Джона

Малий Джон займається тестуванням чисел. Він має два цілих числа А та В. Нехай Джон розглядає деяке ціле число X. Якщо А ≤ X ≤ В, то число X успішно проходить тест Джона. У іншому випадку Джон будує ціле число Y, використовуючи цифри десяткового запису числа X. Спочатку він бере першу цифру (найбільш значущу) числа X, потім — останню цифру X, потім — другу цифру, далі — передостанню і так далі поки не будуть використані всі цифри числа X. Наприклад, якщо X = 1234567, то Y = 1726354, я якщо X = 1020, то Y = 1002. Після побудови числа Y, якщо А ≤ Y ≤ В, то число X проходить тест Джона, інакше X не проходить тест.

Вам необхідно порахувати всі цілі додатні числа, що проходять тест Джона.

Вхідні дані

Два цілих числа А та В через пробіл.

Вихідні дані

Кількість цілих додатних чисел, що проходять тест.

Обмеження

1 ≤ А ≤ В ≤ 1000000000000000000 (10¹⁸).

Примітки

У першому прикладі числа 98, 99, 100, 101, 102, 110 та 120 проходять тест Джона

Входные данные #1

98 102

Выходные данные #1

7

Входные данные #2

123456789 123456789

Выходные данные #2

2

 

-----------------------------------------------------------------------------------------------------------

П'ятірки

Задані два цілих числа N i K. Знайдіть найменше число, більше, чим N, в десятковому записі якого міститься не менше чим K п'ятірок.

Вхідні дані

У першому рядку вхідного файлу міститься два числа N i K(1 ≤N ≤10¹⁵ , 1 ≤ K ≤ 15).

Вихідні дані

Виведіть одне знайдене число.

Входные данные #1

99 1

Выходные данные #1

105

Входные данные #2

595 2

Выходные данные #2

655

Входные данные #3

15187565 3

Выходные данные #3

15187575

Входные данные #4

15187565 2

Выходные данные #4

15187566

-------------------------------------------------------------------------------------------------------------

9. Сформуйте та запишіть висновки опираючись на створені таблиці.
10. Завершіть роботу за комп’ютером.

 

3. Підведення підсумків уроку

Слово вчителя: Сьогодні у нас був дуже змістовний урок, з великою кількість практичних задач і я пропоную Вам відповісти на декілька питань

• Чи сподобалось Вам на уроці, тобто оцініть наш урок за 12-бальною шкалою, де 1- зовсім не сподобалось, незрозуміло пояснено тему, а 12 – доступний виклад матеріалу, цікавий урок.
• Чи задоволені ви своєю роботою.
• Що нового ви дізналися на уроці

 

*Для оцінювання уроку:

 

4. Домашня робота

•                      Вычислите сумму

+  +...+ .

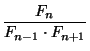•                      Дана последовательность чисел 1, 2, 3, 5, 8, 13, 21, ..., в которой каждое число, начиная с третьего, равно сумме двух предыдущих. В этой последовательности выбрано восемь чисел подряд. Докажите, что их сумма не равна никакому числу рассматриваемой последовательности.
•                      Дана последовательность чисел F₁, F₂, ...;  F₁ = F₂ = 1  и   F_n+2 = F_n + F_n+1.  Доказать, что F_5k делится на 5 при  k = 1, 2, ..
•                      Докажите, что два соседних числа Фибоначчи F_n–1 и F_n  (n ≥ 1)  взаимно просты.
•                      Докажите равенство  (F_n, F_m) = F_{(m, n)}.
•                      Рассматривается последовательность квадратов на плоскости. Первые два квадрата со стороной 1 расположены рядом (второй правее) и имеют одну общую вертикальную сторону. Нижняя сторона третьего квадрата со стороной 2 содержит верхние стороны первых двух квадратов. Правая сторона четвёртого квадрата со стороной 3 содержит левые стороны первого и третьего квадратов. Верхняя сторона пятого квадрата со стороной 5 содержит нижние стороны первого, второго и четвертого квадратов. Далее двигаемся по спирали бесконечно, обходя рассмотренные квадраты против часовой стрелки так, что сторона нового квадрата составлена из сторон трех ранее рассмотренных. Докажите, что центры всех этих квадратов принадлежат двум прямым.