Урок на тему:"Розв'язування нерівностей та систем нерівностей з двома невідомими"

Інтегрований урок з алгебри та інформатики в 9-му класі з поглибленим вивченням математики.

Тема уроку: Розв’язування нерівностей  та систем нерівностей з двома змінними.

Мета уроку: Повторити запис стандартних функцій та алгебраїчних виразів.

За допомогою комп’ютерних технологій розглянути розв’язування нерівностей та систем нерівностей з двома змінними. Ознайомитись з прикладами економічних задач та способами їх розв’язання з використанням комп’ютера. 

Обладнання: комп’ютери з встановленою програмою Advanced Grapher, мультимедійний проектор, екран, картки з завданнями.

 Хід уроку.

І Організаційна частина.  Хвилина з техніки безпеки.

ІІ Вступна частина

З розвитком суспільного життя продовжується розвиток новітніх технологій та застосування їх в повсякденному житті .Майже весь оточуючий нас світ може задати математичними формулами. Рух, приріст чогось, форма об’єкта та інше підвласні математиці . Ми розглянемо деякі приклади , щоб наочно побачити і зрозуміти, що є розв’язками нерівностей з двома невідомими та зробити висновки, щодо доцільності вивчення математики та інформатики.

ІІІ Актуалізація опорних знань, вмінь та навичок учнів (розминка).

Поставити у відповідність функції та їх графіки

Використовуючи правила запису алгебраїчних виразів записати наступні вирази:

При цьому не забувати правила запису алгебраїчних виразів:

1.                 Знак множення не пропускається

2.                 Аргументи стандартних функцій записуються в дужках

3.                 Кількість відкритих дужок дорівнює кількості закритих дужок.

                 І варіант                                  ІІ варіант

               3sin²x_                                      x1  ⁵cosx³

7

ІV Практична робота

Знайти розв’язки нерівностей та систем нерівностей

                     1) x² 1 2x1y                       2) 2xy xy                     3) 1 x (x y²)  0

                        x² y² 5                                           x²  y² 1

                4)_                                            5)_

                        _ xy²                                              _x1  y  2

 Для побудови графіків використовується програма Advanced Grapher. Вікно програми має вигляд:  

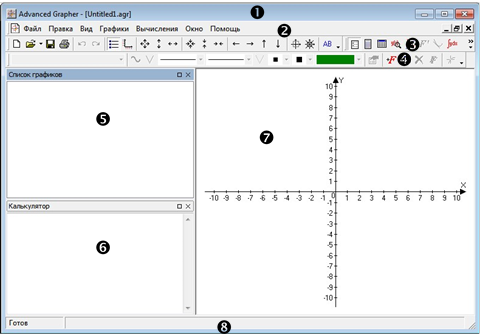
1.                 Рядок заголовка

2.                 Рядок головного меню

3.                 Панель інструментів Стандартна

4.                 Панель інструментів Властивості графіка

5.                 Список графіків

6.                 Калькулятор

7.                 Вікно графіка

8.                 Статусний рядок

Для додавання нового графіка пункт меню Графік—Добавить графік, або кнопка  на панелі інструментів Властивості графіка.

З’являється вікно Додавання графіка 

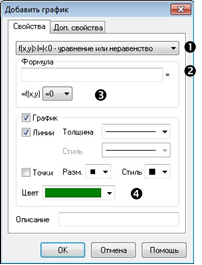
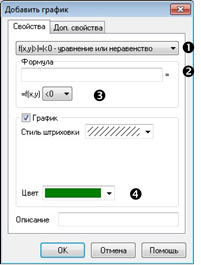
В якому:

1.      Вибір типу графіка

2.      Формула, яка задає графік

3.      Вибір знаку рівняння/нерівності

4.      Вибір кольору графіка або нерівності.

V Побудова математичної моделі економічних задач та їх розв’язання графічним методом.

В практичних задачах часто потрібно не тільки знайти всі розв’язки рівняння чи нерівності, а й необхідно ще вибрати з цих розв’язків найвигідніше.

Задачі учні розв’язують в групах.

Задача1

Три філіали фірми випускають продукцію двох видів А та В. Витрати на продукцію ( в умовних одиницях) подано в таблиці

Робота філій вважається успішною, якщо загальні витрати для філії 1 та філії 3 не менше 12 умовних одиниць, для філії 2 не перевищує 8 умовних одиниць. Скільки кожної продукції повинні виробляти філіали, щоб фірма отримала максимальний прибуток.

Задача2

На двох шахтах добувають руду. На першій 100 т в день, на другій – 200 т в день. Цю руду є можливість обробляти на двох заводах, причому вартість перевезень (в умовних одиницях) однієї тони руди подано в таблиці.

Відомо, що кожен завод може обробляти не  більше 250 т руди. Скільки руди необхідно завозити з кожної шахти на кожний завод, щоб вартість перевезень була найменшою?

VI Підсумки уроку.

Для об’єктивного оцінювання учнів зручно зробити таблицю

1.     Учні показали свої знання та навички при роботі з комп’ютером

2.     Продовжили вчитись знаходити розв’язки нерівностей та систем нерівностей

3.     Ознайомилися з економічними задачаим та одним із способів їх розв’язання

4.     Працюючи в групах продовжують використовувати метод «знаю сам – навчу іншого»

Додаток

Правильні відповіді та розв'язки завдань

І. Розминка

Відповідність: 1 В    2 Д    3 А    4  Б    5  Г Комп'ютерний запис:

                1) 3*sin(x)^2-sqrt(abs(x-2)/3)      2) abs(sqrt(x+1))+(5/7)*cos(x^3)

ІІ. Практична робота. Побудова нерівностей та систем.

                1) sqrt(x^2-1)-sqrt(2*x+1-y^2)≤0               2)abs(2*x-y)-x-y≤0

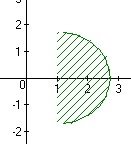
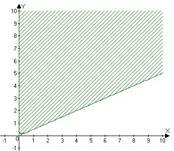
3)sqrt(1-abs(x))*(y-x^2) >0                                                                 4)^_^{x^2+y^2-5 0} _ x*y-2 2

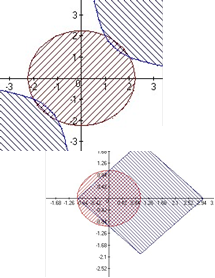
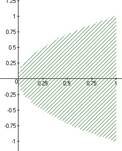
              5)_      x^2 +y^2-1 0         

_abs(x-1)+abs(y)-2 2

ІІІ . Практичні задачі

Задача1 

Нехай х та у –це кількість продукції видів А і В відповідно. 

Тоді (3х+у) – витрати 1 філії, (х+у) –  витрати 2 філії, (х+3у) – витрати 3 філії.

Враховуючи обмеження загальних витрат, запишемо систему нерівностей: _3xy₁₂ прибуток має бути: 4х+3у’max (цільова функція).

 xy8       



^x3y12 

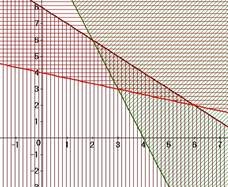За допомогою програми знаходимо множину системи          нерівностей.         При визначені максимуму або мінімуму для економічної задачі знаходяться координати          вершин многокутника,  який є розв’язком системи нерівностей. Маємо: (2;6); (6;2); (3;3). Ці значення підставляємо в цільову функцію.

42+36=26;       46+32=30;       43+33=21 max{26;30;21}=30.

Отже продукцію виду А кожній філії потрібно виробляти в кількості 6 одиниць, продукцію виду В –2 одиниці.

Задача 2

Нехай х – кількість руди, яку перевозять в день з 1–ї шахти на 1–й завод; у – кількість руди, яку перевозять в день з 2 –ї шахти на 1 –й завод;тоді (100-х) – кількість руди, яку перевозять в день з 1–ї шахти на 2–й завод; (200-у) – кількість руди, яку перевозять в день з 2–ї шахти на 2-й завод. Використовуючи обмеження, отримаємо систему:

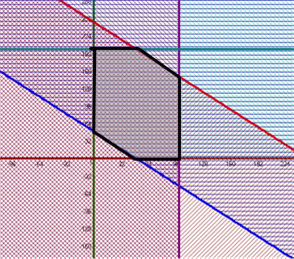
         x0 ^  y 0



x y 250

                 _                                             

_ x y 50  x100



 y 200

Витрати на перевезення:

5х+7у+4(100-х)+5(200-у)=х+2у+1400

Розв’язком задачі на максимум (мінімум) можуть бути координати однієї з вершин многокутника – розв’язку системи:

(50;0); (0;50); (0;200); (50;200); (100;100); (100;0)

Підставляємо в цільову функцію х+2у+1400’min

50+20+1400=1450

0+250+1400=1500

0+2200+1400=1850

100+2100+1400=1700

100+20+1400=1500

Отже, найвигідніший план перевозок подано у вигляді таблиці

IV Фотографії уроку: