Середня лінія трапеції
Тема. Середня лінія трапеції
Мета: сформувати в учнів поняття середньої лінії трапеції; працювати над засвоєнням змісту властивості середньої лінії трапеції, а також схеми її доведення.
Формувати в учнів уміння:
- відтворювати зміст вивчених на уроці тверджень;
- виконувати зображення середньої лінії трапеції;
- використовувати властивість середньої лінії трапеції для розв'язування задач;
- використовувати вивчену властивість у комплексі з раніше вивченими властивостями трапеції.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Середня лінія трапеції».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Математичний диктант
Варіант 1
- Дві сторони трикутника сполучили відрізком, не паралельним до третьої сторони. Чи є цей відрізок середньою лінією трикутника?
- У трикутнику ABC сторона АВ дорівнює 6 м Чому дорівнює середня лінія трикутника ABC, яка паралельна стороні АВ?
- Точки М, Р і О — середини сторін трикутника ABC. Знайдіть периметр трикутника ABC, якщо сторони трикутника МРО дорівнюють 3 см, 4 см і 5 см.
-
Кінці відрізка АВ лежать на двох сторонах трикутника, а довжина
цього відрізка дорівнює половині третьої сторони. Чи обов'язково
АВ є середньою лінією трикутника?
Варіант 2
- Точки А і В є серединами двох сторін трикутника. Як називається відрізок АВ?
- У трикутнику ABD середня лінія паралельна стороні BD і дорівнює 4 см. Чому дорівнює сторона ВD?
- Точки А, В і С — середини сторін трикутника МРО. Знайдіть периметр трикутника ABC, якщо сторони трикутника МРО дорівнюють 5 дм, 6 дм і 7 дм.
-
Кінці відрізка KL лежать на двох сторонах трикутника. Відрізок KL
паралельний до третьої сторони трикутника і дорівнює чверті його
довжини. Чи є відрізок KL середньою лінією цього трикутника?
ІІІ. Формулювання мети і завдань уроку
Учитель повідомляє учням про те, що на уроці вони нарешті будуть вивчати ту властивість трапеції, заради якої було вивчено теорему Фалеса та поняття і властивості середньої лінії трикутника. Вивчення означення та властивості цього нового елемента трапеції, а також оволодіння способами використання вивчених на уроці тверджень під час розв'язування задач і є основною метою уроку.
IV. Актуалізація опорних знань
З метою свідомого сприйняття учнями змісту означення, властивості та способів доведення властивості середньої лінії трапеції та подальшого оволодіння учнями способами дій під час застосування названих понять слід активізувати знання і вміння учнів щодо означення трапеції та її елементів, властивостей трапецій; ознак рівності трикутників, а також теореми Фалеса.
|
1 |
|
Знайдіть на рисунку трапеції. Назвіть їхні основи і бічні сторони |
|
2 |
|
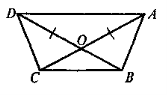
Дано: ABCD — рівнобічна трапеція. Довести: АС = BD |
|
3 |
|
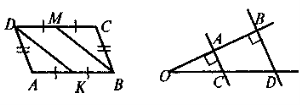
Дано: ABCD — трапеція, ВК — бісектриса кута В, CM — бісектриса кута С.
Довести: СМ |
|
4 |
|
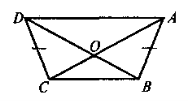
Дано: ABCD — трапеція, AO = OD. Довести: AB = DC |
|
5 |
|
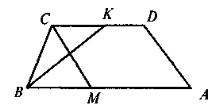
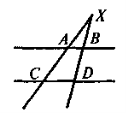
Дано: AB || CD, AX = AC, СХ = 10 cm, BD менше від DX на 3 см. Знайти: BD |
|
6 |
|
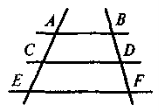
Дано: AB || CD || EF, АС = BD + BF = 15. Знайти: DF |
V. Засвоєння знань
План вивчення нового матеріалу
- Означення середньої лінії трапеції.
- Властивість середньої лінії трапеції.
|
Конспект 8 |
|
|
Середня лінія трапеції |
|
|
|
Означення, Середньою лінією трапеції називається відрізок, що сполучає середини бічних сторін трапеції. |
|
|
|
|
Властивості |
|
|
|
1. Якщо MN — середня лінія трапеції ABCD (BC || AD), то: MN || AD (BC) і
MN = |
|
2*. Середня лінія трапеції ділить навпіл будь-який відрізок, кінці якого лежать на основах трапеції |
|
|
|
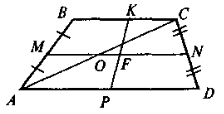
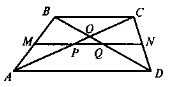
3. Якщо ABCD - трапеція (BC\\AD), 0 — точка перетину діагоналей, MN — середня лінія, то Р і Q — середини діагоналей АС і BD:
QN= |
Слід зазначити, що зміст матеріалу нового підручника з теми «Середня лінія трапеції» майже відтворює зміст відповідних розділів підручника О.В.Погорєлова. Тому вивчення теоретичного матеріалу (які і на попередніх трьох уроках) можна вести за традиційною схемою, акцентуючи увагу учнів на таких моментах:
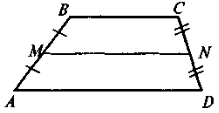
- сформулювавши означення середньої лінії трапеції, слід звернути увагу учнів на те, що, на відміну від середньої лінії трикутника (сполучає середини двох будь-яких сторін трикутника), вона сполучає середини бічних сторін трапеції, а тому в будь-якій трапеції можна провести лише одну середню лінію (для допитливих учнів можна дати інформацію про існування такого поняття як «друга середня лінія трапеції», але в цьому разі треба наголосити на тому, що поняття середньої лінії трапеції та другої середньої лінії трапеції не ідентичні). Закріплення контрольних моментів відбувається під час розв'язування усних вправ. Чи є відрізок MN, що зображений на рис. 1, середньою лінією трапеції ABCER ABCD — трапеція (ВС || AD);
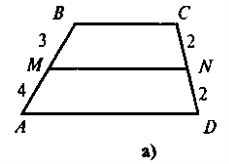
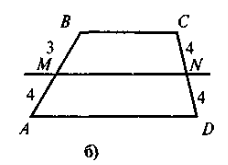
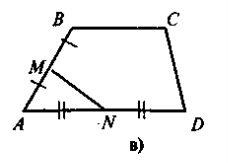
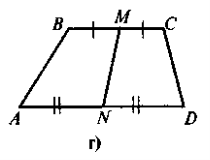
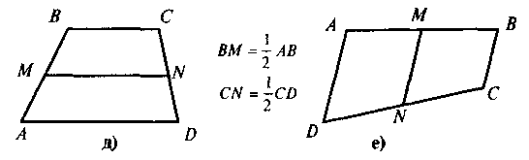
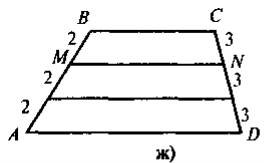
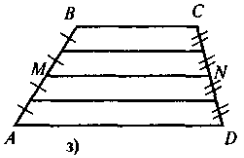
Рис. 1
- вивчення змісту теореми про властивість середньої лінії трапеції можна провести за підручником (форма роботи аналогічна до тієї, що була використана на попередніх уроках) або розпочати із задачі на повторення, яка була задана додому (див. попередній урок), і здобути формулювання властивості середньої лінії трапеції як свого роду наслідок з доведеної рівності трикутників. Для допитливих учнів можна запропонувати «винайти» інший спосіб доведення;
- закріплення змісту теореми про властивість середньої лінії трапеції проводимо під час виконання усних вправ;
- до властивості середньої лінії трапеції, що міститься у формулюванні теореми, можна додати властивості, які безпосередньо випливають із доведеної або з теореми Фалеса (див. конспект 8); загальне формулювання цих додаткових властивостей середньої лінії трапеції та її відрізків суттєво спрощує розв'язування багатьох задач (див. усні вправи вище).
Виконання усних вправ
- Середини основ трапеції сполучені відрізком. Чи є він середньою лінією трапеції?
- Чи може середня лінія трапеції бути меншою від обох її основ; дорівнювати одній з основ?
- Чи може середня лінія трапеції проходити через точку перетину діагоналей?
- Знайдіть х (рис. 2):
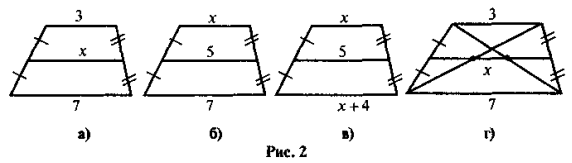
Виконання письмових вправ
- Знайдіть:
а) середню лінію трапеції з основами 8 см і 12 см;
б) основи трапеції, діагональ якої ділить середню лінію на відрізки завдовжки 3 см і 4 см.
-
Основи трапеції 8 см і 12 см. Знайдіть відрізки середньої лінії, які
містяться між діагоналями трапеції. -
Середня лінія трапеції у 3 рази більша за меншу основу і на 8 см
менша за більшу основу. Знайдіть основи трапеції. -
Основи трапеції дорівнюють 10 см і 6 см. її бічну сторону поділено
на 4 рівні частини і через точки поділу проведено прямі, паралельні
основам. Знайдіть довжини відрізків цих прямих, які містяться між
сторонами трапеції.
VII. Підсумки уроку
У наведених твердженнях знайдіть та виправте помилки.
- Середня лінія трапеції сполучає середини двох сторін трапеції.
- Середня лінія сполучає середини основ трапеції.
- Середня лінія трапеції сполучає бічні сторони трапеції.
- Середня лінія трапеції дорівнює сумі основ.
- Середня лінія трапеції дорівнює півсумі сторін трапеції.
- Середня лінія трапеції паралельна до сторони трапеції.
- Середня лінія трапеції проходить через точку перетину діагоналей трапеції.
VIII. Домашнє завдання
Вивчити зміст означення, властивості та доведення властивості середньої лінії трапеції.
Розв'язати задачі.
- Знайдіть:
а) середню лінію рівнобедреної трапеції з бічною стороною 5 см і периметром 26 см;
б) основи трапеції, якщо одна з них більша за іншу на 6 см, а середня лінія трапеції дорівнює 5 см.
- Знайдіть середню лінію трапеції, якщо її основи дорівнюють: а) 7 см і 9 см; в) а і 7а.
- Знайдіть основу трапеції, якщо її інша основа і середня лінія відповідно дорівнюють: а) 9 см і 5 см; б) 3а і 7а; в) а і b.
- Відрізки, на які діагональ трапеції ділить середню лінію, відносяться як 5:9, а їх різниця дорівнює 12 см. Знайдіть основи трапеції. Повторити властивість середньої лінії трикутника.

про публікацію авторської розробки
Додати розробку