СЕРЕДНЯ ШВИДКІСТЬ НЕРІВНОМІРНОГО РУХУ.
| Технічні засоби навчання, наочні посібники 1. Комп'ютер, Цифрові навчальні ресурси: 15-001 Інтерактивний плакат «Середня швидкість». Міжпредметні зв'язки: природознавство, математика.Методи навчання: |
| Бесіда |
| Робота над помилками |
| Розв'язування задач |
| Фронтальна робота |
| Дидактична гра «Мікрофон» |
| Бесіда |
Тема: Прямолінійний нерівномірний рух. Середня швидкість нерівномірного руху.
Мета
Навчальна: познайомити учнів із новим типом задач на знаходження середньої швидкості руху; увести поняття прямолінійного нерівномірного руху як одного з поширених у природі.
Розвивальна: продовжити формування вмінь аналізувати умову задачі, знаходити оптимальні способи її розв’язання; аналізувати отримані відповіді; продовжити формування алгоритмічного підходу до розв’язування задач на розрахунок середньої швидкості руху.
Виховна: продовжити формування вмінь учнів акуратно оформляти розв’язки задач, брати участь в обговоренні ходу розв’язування задач.
Учні мають:
знати: визначення середньої швидкості, одиниці часу, шляху, швидкості, формулу визначення шляху, середньої швидкості прямолінійного нерівномірного руху;
уміти: розв’язувати задачі на застосування формули середньої швидкості, представляти результати у вигляді таблиці й графіка.
Технічні засоби навчання, наочні посібники
1. Комп’ютер,
Цифрові навчальні ресурси: 15-001 Інтерактивний плакат «Середня швидкість».
Міжпредметні зв’язки: природознавство, математика.
План заняття
|
Час |
Метод навчання |
Зміст роботи |
Наочні посібники, ТЗН |
|
1 хв |
Бесіда |
І. Організаційний момент |
|
|
7 хв |
Робота над помилками |
ІІ. Аналіз результатів самостійної роботи |
|
|
10 хв |
Розв’язування задач |
ІІІ. Активізація розумової діяльності |
|
|
10 хв |
|
IV. Вивчення нового матеріалу |
Інтерактивний плакат «Середня швидкість» |
|
15 хв |
Фронтальна робота |
V. Закріплення нового матеріалу |
|
|
1 хв |
Дидактична гра «Мікрофон» |
VI. Підбиття підсумків уроку |
|
|
1 хв |
Бесіда |
VII. Домашнє завдання |
|
ХІД УРОКУ
І. Організаційний момент
ІІ. подорож колобка
ІІІ. Активізація розумової діяльності
Для введення понять прямолінійного нерівномірного руху й середньої швидкості такого руху вчитель пропонує учням виконати кілька завдань, що дозволяють підвести школярів до розуміння загальності нерівномірного прямолінійного руху.
«BugattiVeyron» — найшвидший та один із найдорожчих автомобілів за всю історію людства. Максимальна швидкість більша від 407![]() . Запишіть її в одиницях СІ. 407
. Запишіть її в одиницях СІ. 407![]() = 131
= 131![]() .
.
|
|
|
|
|
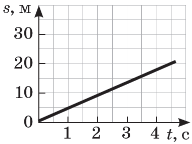
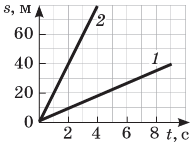
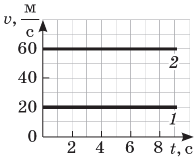
За графіком визначте швидкість руху тіла. |
У скільки разів швидкість другого тіла більша від швидкості першого? |
Визначте шляхи, пройдені першим і другим тілом за 4 с. Яке тіло подолало більший шлях? Чому? |
Крапельницю встановили на іграшковий заводний автомобіль. Опишіть вид руху цієї системи. Як рухається, чому можна зробити такий висновок? Наведіть приклади подібного руху. Чи можна рух автомобіля назвати рівномірним?

Проаналізуйте швидкості, наведені в цій таблиці. Дайте відповіді на наведені нижче запитання.
Швидкості руху в природі (![]() )
)
|
Равлик |
0,0014 |
|
Звук у повітрі |
331 |
|
Муха |
5 |
|
Обертання Місяця навколо Землі |
1000 |
|
Грач |
20 |
|
Обертання Землі навколо Сонця |
30 000 |
|
Страус |
22 |
|
Світло у вакуумі |
300 000 000 |
1. Чи обов’язково всі об’єкти, указані в цій таблиці, рухаються рівномірно?
2. Які об’єкти рухаються нерівномірно, що може вплинути на їхній рух?
IV. Вивчення нового матеріалу
Нерівномірність руху ми можемо виявити під час підходу потяга до станції, навіть без секундоміра. Грубі вимірювання покажуть нам, що проміжки часу, за які потяг проходить відстані від одного телеграфного стовпа до іншого, стають усе більшими й більшими. З тією малою мірою точності, яку дає вимірювання часу за годинником, рух потяга на перегоні рівномірний, а під час підходу до станції — нерівномірний.
Коли мова йдеться про нерівномірний рух, не можна говорити про якусь певну швидкість, оскільки відношення пройденого шляху до відповідного проміжку часу не однакове для різних ділянок, як це мало місце для рівномірного руху. Якщо, проте, нас цікавить рух тільки на якій-небудь певній ділянці шляху, то цей рух можна охарактеризувати в цілому, увівши поняття середньої швидкості руху: середньою швидкістю vсер руху на цій ділянці шляху називають відношення довжини s цієї ділянки до проміжку часу t, за який ця ділянка пройдена, тобто
![]() .
.
Звідси видно, що середня швидкість дорівнює швидкості такого рівномірного руху, під час якого тіло пройшло б цю ділянку шляху за той самий проміжок часу, що й за дійсного руху. Як і в разі рівномірного руху, можна користуватися формулою ![]() для визначення шляху, пройденого за цей проміжок часу на певній середній швидкості, і формулою для визначення часу
для визначення шляху, пройденого за цей проміжок часу на певній середній швидкості, і формулою для визначення часу ![]() , за який пройдено цей шлях із цією середньою швидкістю. Але користуватися поданими формулами можна тільки для тієї певної ділянки шляху й для того проміжку часу, для яких ця середня швидкість була розрахована.
, за який пройдено цей шлях із цією середньою швидкістю. Але користуватися поданими формулами можна тільки для тієї певної ділянки шляху й для того проміжку часу, для яких ця середня швидкість була розрахована.
Наприклад, знаючи середню швидкість на ділянці шляху AB і довжину AB, можемо визначити час, за який була пройдена ця ділянка, але не можна знайти час, за який була пройдена половина ділянки AB, оскільки середня швидкість на половині ділянки за нерівномірного руху загалом не дорівнюватиме середній швидкості на всій ділянці.
Якщо для будь-яких ділянок шляху середня швидкість виявилася однаковою, то це означає, що рух рівномірний і середня швидкість дорівнює швидкості цього рівномірного руху.
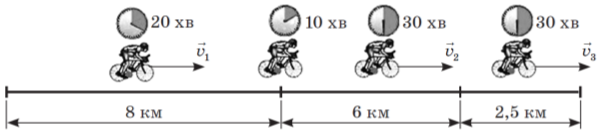
Знайдіть середню швидкість руху велосипедиста на всьому його шляху з одного міста в інше, якщо за 20 хвилин він проїхав 8 км, відпочивши 10 хвилин, проїхав іще 6 км за 30 хвилин. А решту 2,5 км пройшов пішки за 30 хвилин. Знайдіть швидкості руху велосипедиста на кожному відрізку шляху.
v1 = _____![]() = _____
= _____![]() , v2 = _____
, v2 = _____![]() , _____
, _____![]() , v3=_____
, v3=_____![]() , _____
, _____![]() ,
,
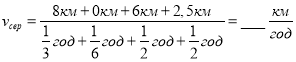
Використовуючи цей рисунок, складіть умову задачі на побудову графіків і розв’яжіть її.
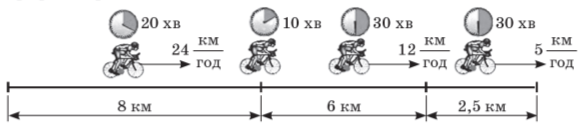
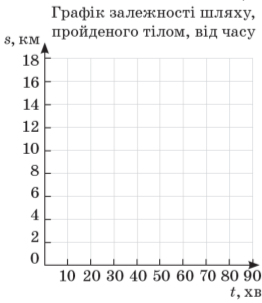
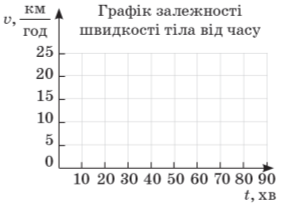
Якщо середня швидкість відома за окремі послідовні проміжки часу, то можна знайти середню швидкість і за сумарний час руху.
Щоб обчислити середню швидкість у загальному випадку, коли відомі середні швидкості руху v1, v2, v3, ..., з якими тіло рухалося впродовж послідовних проміжків часу t1, t2, t3, ..., треба скористатися формулою
![]()
Наприклад, відомо, що поїзд рухався впродовж двох годин, причому його середня швидкість за перші 10 хвилин дорівнювала 18![]() , за наступні півтори години — 50
, за наступні півтори години — 50![]() , а за решту часу — 30
, а за решту часу — 30![]() . Знайдемо довжини шляхів, пройдених за окремі проміжки часу:
. Знайдемо довжини шляхів, пройдених за окремі проміжки часу: ![]() км,
км, ![]() км,
км,![]() км. Значить, загальна довжина шляху, пройденого поїздом, — s = 3+ 75 + 10 = 88 км. Оскільки весь цей шлях був пройдений за дві години, шукана середня швидкість —
км. Значить, загальна довжина шляху, пройденого поїздом, — s = 3+ 75 + 10 = 88 км. Оскільки весь цей шлях був пройдений за дві години, шукана середня швидкість — ![]() .
.
Важливо відзначити, що в загальному випадку середня швидкість не дорівнює середньому значенню від середніх швидкостей на окремих ділянках шляху.
V. Закріплення нового матеріалу
Чоловік зазвичай долає відстань від будинку до станції за час t0 = 12 хв, проходячи відстань l = 800 м. Одного разу, пройшовши чверть шляху, він згадує, що не вимкнув електроприлади, і повертається додому, вимикає їх, витрачаючи час τ = 2 хв, і знову йде на станцію. З якою найменшою швидкістю потрібно рухатися чоловіку після того, як він повернувся додому, щоб встигнути на станцію у звичайний час (і не запізнитися на електричку)?
Розв’язок
1. Зазвичай людина рухається зі швидкістю
![]() .
.
2. Пройшовши з такою швидкістю чверть шляху, чоловік витратив час
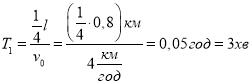 .
.
Значить, у його розпорядженні залишився час
Т2 = t0 − T1 = 12 – 3 = 9 хв.
3. За час Т2 чоловік повинен подолати шлях до будинку, а потім знову до станції: s = 1 км і, крім того, частина часу (τ =2 хв) витратити. Тому шлях s чоловікові доведеться долати за час
T = Т2 − τ = 9 – 2 = 7хв = ![]() год,
год,
тобто з не меншою швидкістю, ніж
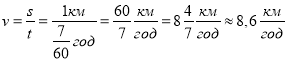 .
.
Перевірте, що, добігши до будинку зі швидкістю ![]() , а потім, крокуючи зі швидкістю
, а потім, крокуючи зі швидкістю ![]() , чоловік прийде на станцію вчасно.
, чоловік прийде на станцію вчасно.
Відповідь: чоловікові необхідно рухатися з не меншою швидкістю, ніж ![]() . Зверніть увагу, що середня швидкість за час від початку руху до його закінчення (t = 12 хвилин) становить
. Зверніть увагу, що середня швидкість за час від початку руху до його закінчення (t = 12 хвилин) становить
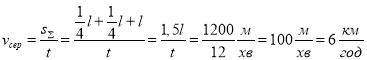 .
.
Знайдене значення vсeр у півтора рази вище, ніж v0, і показує, з якою початковою швидкістю слід виходити чоловікові з будинку, якщо він забудькуватий.
На рисунку показаний графік залежності швидкості чоловіка від часу для випадку, коли він біжить додому зі швидкістю v1 = 3v0 = 12![]() , а потім іде до станції дуже швидким кроком зі швидкістю v2 = 2v0 = 8
, а потім іде до станції дуже швидким кроком зі швидкістю v2 = 2v0 = 8![]() . Штрихпунктирною лінією позначений графік руху зі швидкістю v0, а тонкою лінією — зі швидкістю vсeр = 6
. Штрихпунктирною лінією позначений графік руху зі швидкістю v0, а тонкою лінією — зі швидкістю vсeр = 6![]() .
.
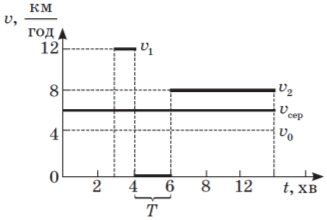
Підрахуємо середнє арифметичне для значень швидкості v0, v1, v2:
![]() .
.
Це значення не дорівнює значенню середньої швидкості vсeр. Переконайтеся в цьому й не робіть надалі поширену помилку: не намагайтеся шукати середню швидкість як середнє арифметичне значення (воно не має фізичного сенсу!).
Автомобіль проїжджає першу третину шляху рівномірно зі швидкістю v1 = 108![]() , а інші дві третини — зі швидкістю v2 = 72
, а інші дві третини — зі швидкістю v2 = 72![]() . Знайдіть середню швидкість автомобіля.
. Знайдіть середню швидкість автомобіля.
Розв’язок
Неправильно вважати, що середня швидкість збігається із середнім арифметичним значенням v1 і v2, яке становить
![]() .
.
1. Знайдемо час t1 руху зі швидкістю v1, вважаючи, що весь шлях дорівнює L [км]. З умови зрозуміло, що
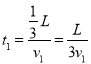 .
.
2. Час t2 руху на ділянці шляху, що залишилася, становить
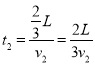 .
.
3. Отже, час на подолання шляху L становить
![]() .
.
4. За визначенням
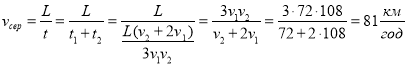 .
.
Відповідь: середня швидкість v сер = 81![]() .
.
Значення середньої швидкості збігається із середнім арифметичним значенням швидкості тільки в одному окремому випадку, коли тіло рухається з різними швидкостями так, що між послідовними моментами зміни (перемикання) швидкості проходить однаковий час T. Таким чином, тіло рухається зі швидкістю v1 упродовж часу t1 = T, зі швидкістю v2 упродовж часу t2 = T, зі швидкістю v3 впродовж часу t3 = T тощо. Якщо впродовж шляху швидкість змінювалася n разів, то пройдений шлях
![]() .
.
Час t, за який пройдений шлях, становить
![]() .
.
За визначенням
![]()
Не заборонено для цього окремого випадку рухатися зі швидкістю v0 = 0, тобто робити зупинки. Але час зупинки повинен становити t0 = T.
Рефлексія.
VIІ. Домашнє завдання
- Вивчити відповідний параграф підручника, відповісти на запитання після параграфа, виконати завдання за задачником.
- Розв’язати задачі:
1. Поїзд проходить перші 10 км із середньою швидкістю 30![]() , другі 10 км — із середньою швидкістю 40
, другі 10 км — із середньою швидкістю 40![]() , треті 10 км — із середньою швидкістю 60
, треті 10 км — із середньою швидкістю 60![]() . Яка була середня швидкість поїзда на всьому 30-кілометровому відрізку шляху?
. Яка була середня швидкість поїзда на всьому 30-кілометровому відрізку шляху?
2. Показати, що середня швидкість на всьому шляху буде більшою від найменшої із середніх швидкостей на окремих ділянках і меншою від найбільшої з них.


про публікацію авторської розробки
Додати розробку