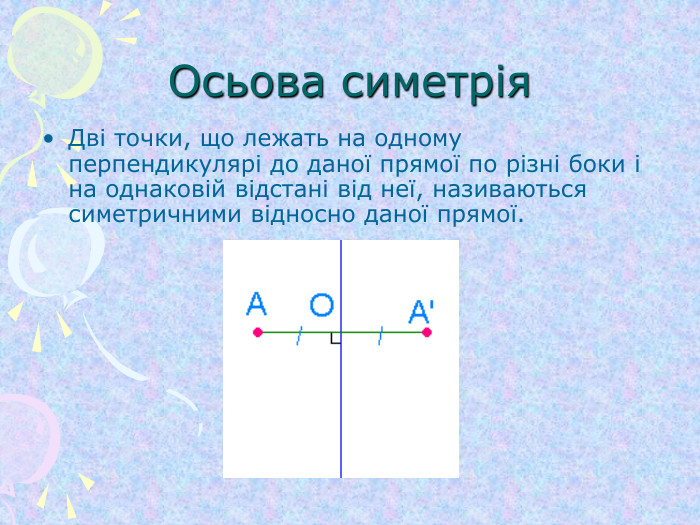
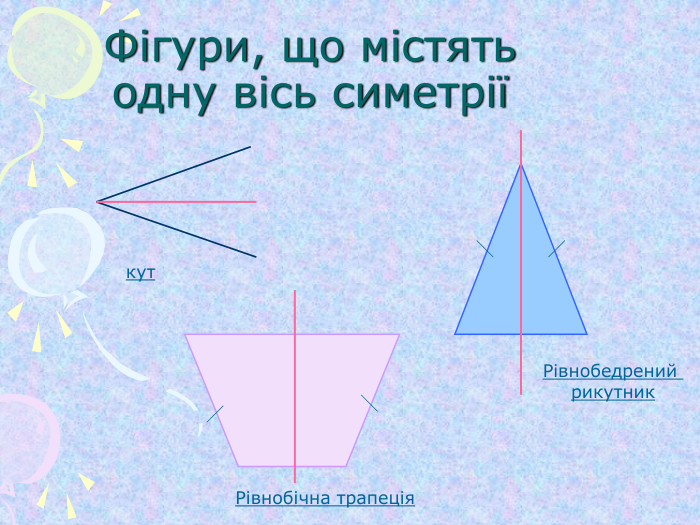
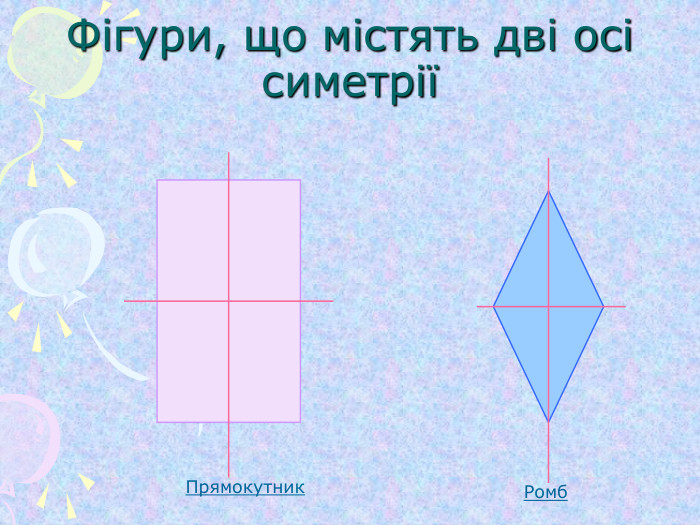
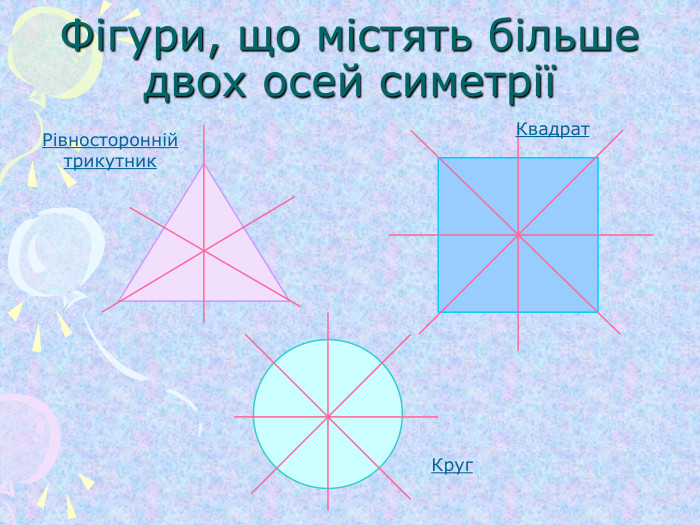
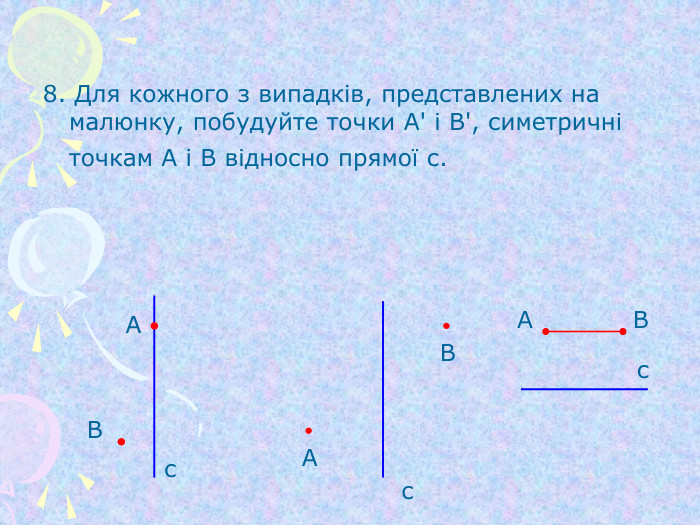
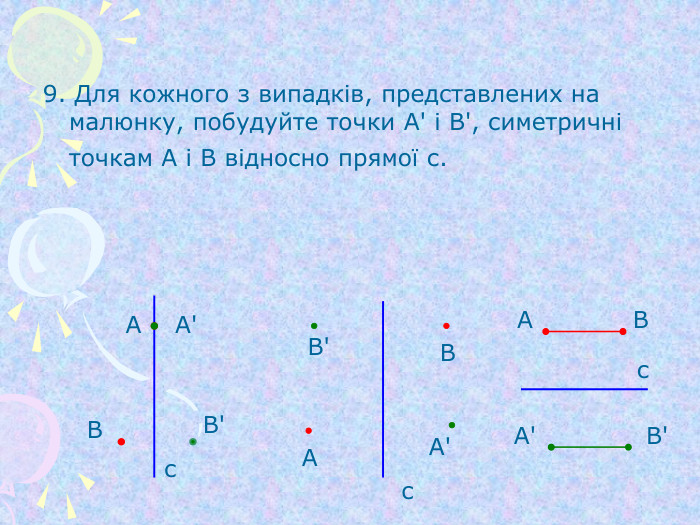
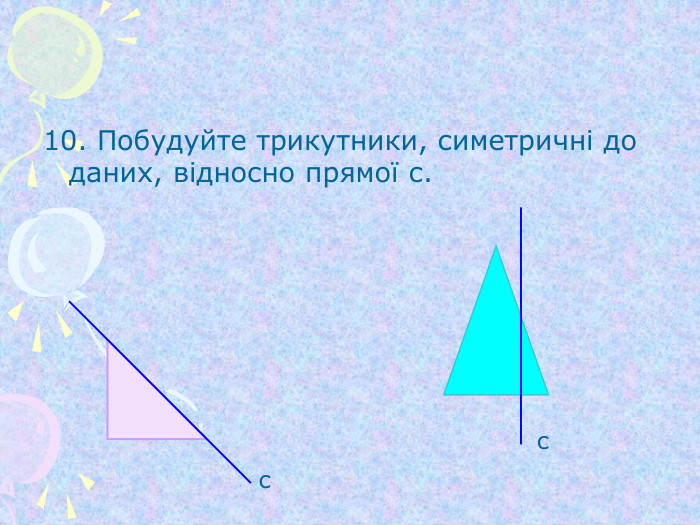
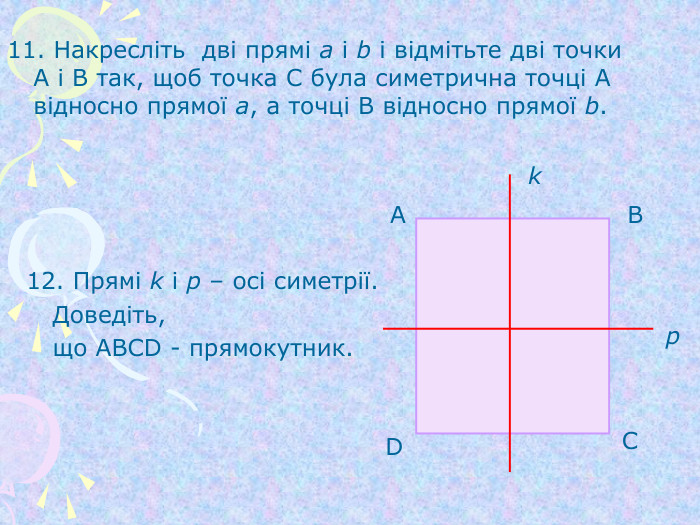
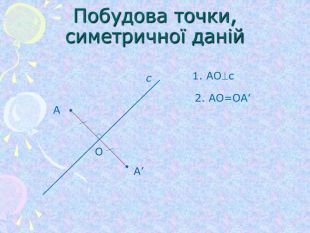
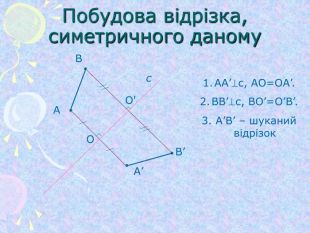
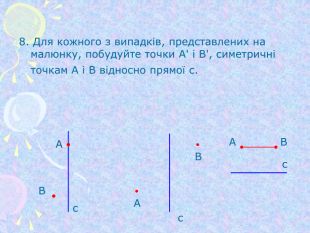
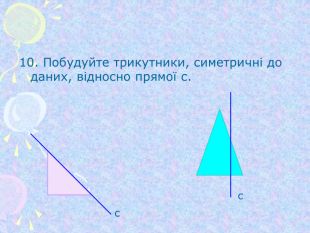
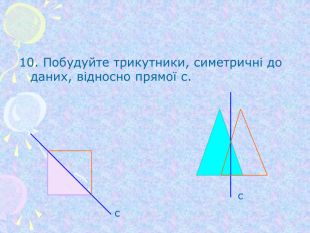
Симетрія відносно початку координат та координатних площин (1)

Вивчаємо тему: Осьова симетрія

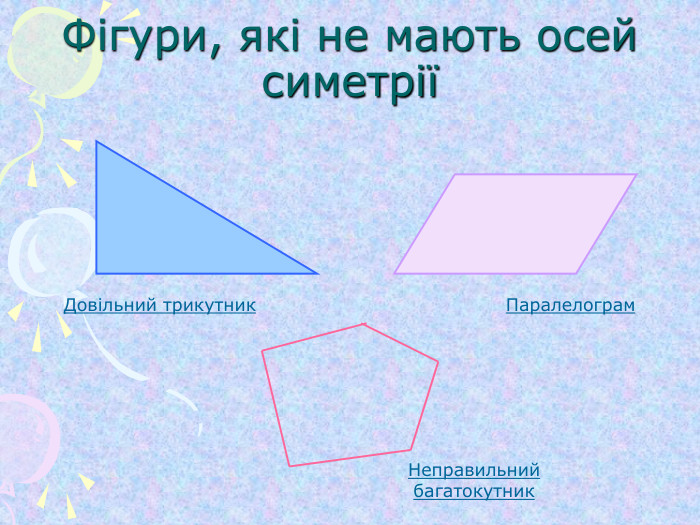
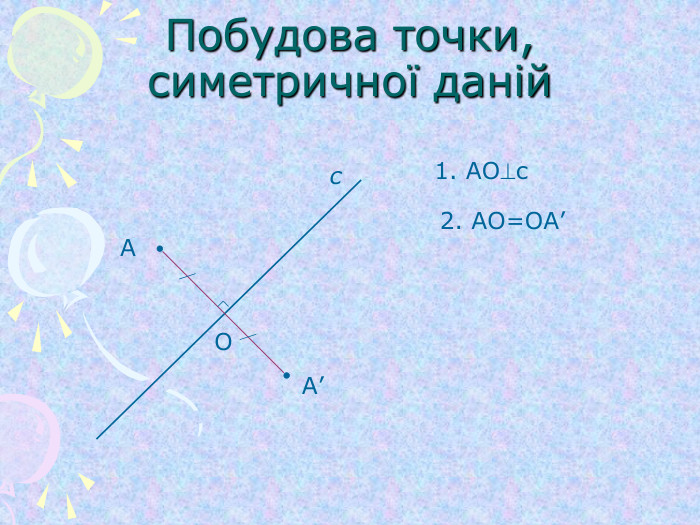
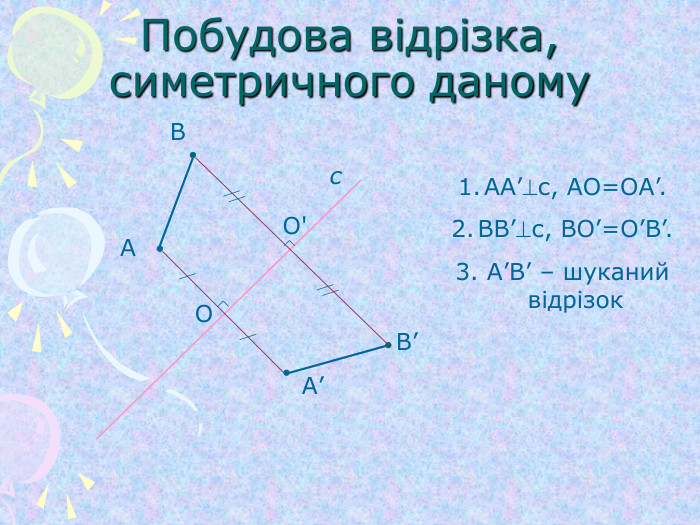
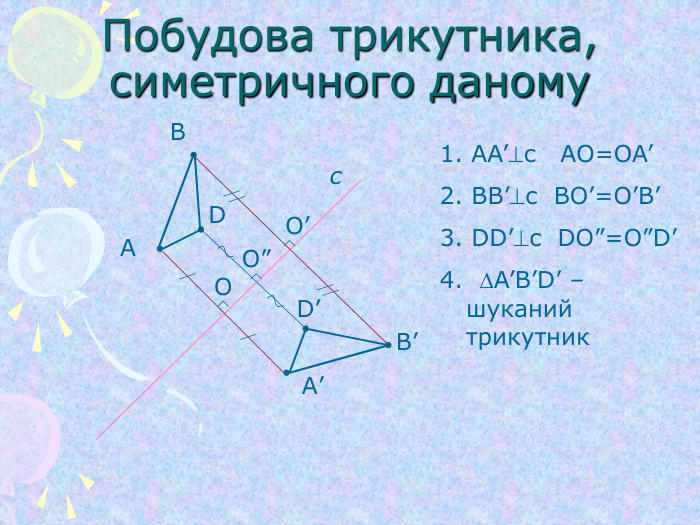
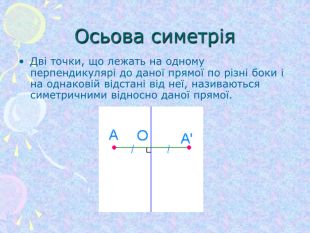
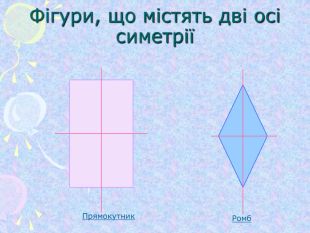
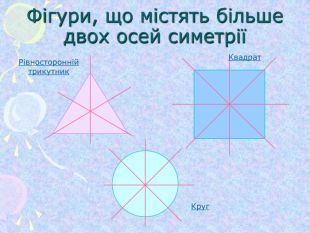
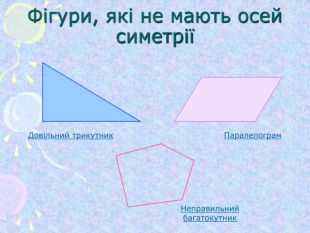
Означення Симетрія (від гр. Symmetria – співрозмірність), в широкому змісті – незмінність структури нематеріального об'єкту. Симетрія відіграє надзвичайно велику роль в природі, в мистецтві та архітектурі. ЇЇ помічають навіть в музиці та поезії. Найбільш поширена симетрія в природі кристалів, рослин та тварин. Оглянемось навколо і ми в полоні симетрії…

Симметрія в природі

В архітектурі

Осьова симетрія Дві точки, що лежать на одному перпендикулярі до даної прямої по різні боки і на однаковій відстані від неї, називаються симетричними відносно даної прямої.

Фігура називається симетричною відносно даної прямої а, якщо для кожної точки фігури симетрична їй точка відносно прямої а також належить фігурі. а

Фігури, що містять одну вісь симетрії кут Рівнобедрений рикутник Рівнобічна трапеція

Фігури, що містять дві осі симетрії Прямокутник Ромб

Фігури, що містять більше двох осей симетрії Рівносторонній трикутник Квадрат Круг

Фігури, які не мають осей симетрії Довільний трикутник Паралелограм Неправильний багатокутник

Побудова точки, симетричної даній відрізка, симетричного даному трикутника, симетричного даному

Побудова точки, симетричної даній А с А’ 1. АОс О 2. АО=ОА’

Побудова відрізка, симетричного даному А с А’ В В’ O O' АА’с, АО=ОА’. ВВ’с, ВО’=О’В’. 3. А’В’ – шуканий відрізок

Побудова трикутника, симетричного даному А с А’ В В’ D D’ 1. AA’c AO=OA’ 2. BB’c BO’=O’B’ 3. DD’c DO”=O”D’ 4. A’B’D’ – шуканий трикутник O O” O’

Задачі 1. Відрізок АВ, перпендикулярний до прямої с, перетинає її в точці О так, що АО≠ОВ. Чи симетричні точки А і В відносно прямої с? 2. Пряма а перетинає відрізок МК в його середині під кутом, що не є прямим. Чи симетричні точки М і К відносно прямої а? 3. Зобразіть точку А що лежить в першій чверті Точка В симетрична точці А відносно осі y. Точка С симетрична точці В відносно осі х. Точка D симетрична точці С відносно осі у. Що ви можете сказати: про точки A і D про фігуру ABCD при якій умові ABCD буде квадратом?

4. Відносно якої з координатних осей симетричні точки М(7;2) і К(-7;2)? 5. Точки А(5;…) і В(…;2) симетричні відносно осі Ох. Запишіть їх пропущенні координати. 6. Точка А(-2;3), В - симетрична їй точка відносно осі Ох, точка С – симетрична точці В відносно осі Оу. Знайдіть координати точки С. 7. Точка А(3;1), В – симетрична їй точка відносно прямої у = х. Знайдіть координати точки В.

Перевір себе!!! 4. Відповідь: Оу. 5. Відповідь : А(5;-2) і В(5;2). 6. Відповідь : С(2;-3). 7. Відповідь : В(1;3)

8. Для кожного з випадків, представлених на малюнку, побудуйте точки А' і В', симетричні точкам А і В відносно прямої с. В А с А В с А В с

9. Для кожного з випадків, представлених на малюнку, побудуйте точки А' і В', симетричні точкам А і В відносно прямої с. В В' А А' с А А' В В' с А В с А' В'

10. Побудуйте трикутники, симетричні до даних, відносно прямої с. с с

10. Побудуйте трикутники, симетричні до даних, відносно прямої с. с с

12. Прямі k і р – осі симетрії. Доведіть, що ABCD - прямокутник. k р А В С D 11. Накресліть дві прямі а і b і відмітьте дві точки А і В так, щоб точка С була симетрична точці А відносно прямої а, а точці В відносно прямої b.

висновок Симетрію можна знайти майже всюди, якщо знати, як її шукати. Багато століть люди з давніх часів володіли уявленням про симетрію як про гармонію. З допомогою симетрії, людина завжди прагнула, за словами німецького математика Германа Вейля, «досягнути і створити порядок, красу і досконалість».