Співвідношення між сторонами і кутами трикутника. Нерівність трикутника
Про матеріал
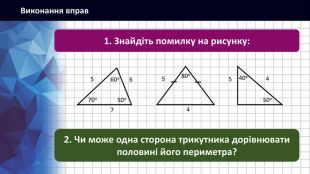
Розробка презентації до уроку з геометрії у 7 класі "Співвідношення між сторонами і кутами трикутника. Нерівність трикутника" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку














-

Кравченко Лілія
28.02.2024 в 16:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сімаченко Олена
27.02.2023 в 19:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
13.02.2023 в 22:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Писаренок Зінаїда Іванівна
23.02.2021 в 09:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Назаренко Віра Михайлівна
30.01.2021 в 18:56
Дуже добре зроблена робота. Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука