Тема "Сума кутів трикутника"(конспект+презентація+додатки)
- Задачі №1,2.docx docx
- Зміст практичного кейсу.docx docx
- ПІБ учня тест.docx docx
- подложка.docx docx
- Показати всі файли
![]()
![]()

![]()
![]()
 3 лютого
3 лютого
Класна робота
Тема:
Зміст практичного кейсу №1
Група перша.
- Будуйте трикутник з двома прямими кутами.
А = 90 0
В = 30 0
С = 90 0

3 лютого
Класна робота
Тема:
Зміст практичного кейсу №1
Група друга
- Будуйте трикутник з двома тупими кутами.
А = 120 0
В = 50 0
С = 100 0
 3 лютого
3 лютого
Класна робота
Тема:
Зміст практичного кейсу №1
Третя група
- Будуйте трикутник з тупим і прямим кутом.
А = 120 0
В = 30 0
С = 90 0
Зміст практичного кейсу №2
Група перша.
На парті лежать трикутники.
Шляхом перегинання отримати прямокутник і зробити висновок про суму кутів трикутника.
Зміст практичного кейсу №2
Група друга
На парті лежать трикутники. Розрізати трикутники на три частини, щоб вийшло три кути. Спробувати визначити їх суму. Зробити висновок.
Зміст практичного кейсу №2
Третя група
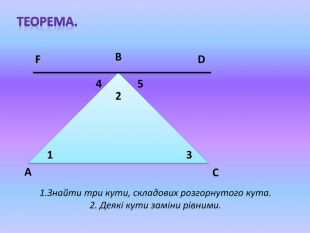
|
ﮮА |
= |
|
ﮮВ |
= |
|
ﮮС |
= |
|
ﮮА+ ﮮВ+ ﮮС |
= |
На картці побудований трикутник. Виміряти кути трикутника за допомогою транспортира. Дані вимірювань занести в таблицю. Зробіть висновок про суму кутів трикутника.
Зміст теоретичного кейсу №3
|
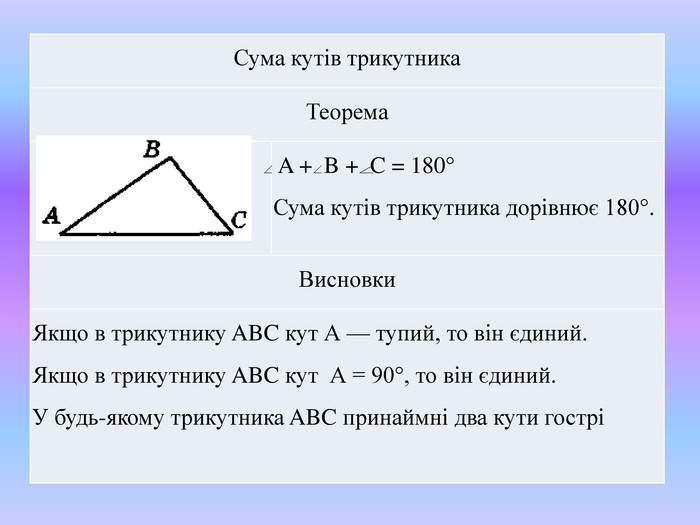
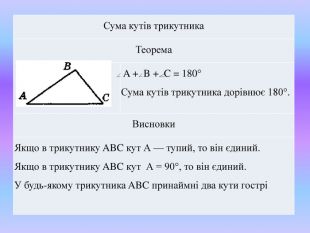
Сума кутів трикутника |
|
|
Теорема |
|
|
|
Сума кутів трикутника дорівнює 180°. |
|
Висновки |
|
|
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі |
|
Зміст теоретичного кейсу №3
|
Сума кутів трикутника |
|
|
Теорема |
|
|
|
Сума кутів трикутника дорівнює 180°. |
|
Висновки |
|
|
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі |
|
Зміст теоретичного кейсу №3
|
Сума кутів трикутника |
|
|
Теорема |
|
|
|
Сума кутів трикутника дорівнює 180°. |
|
Висновки |
|
|
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі |
|
Зміст практичного кейсу №4
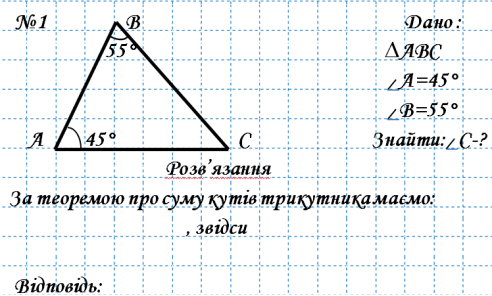
Зміст практичного кейсу №4

Зміст практичного кейсу №4

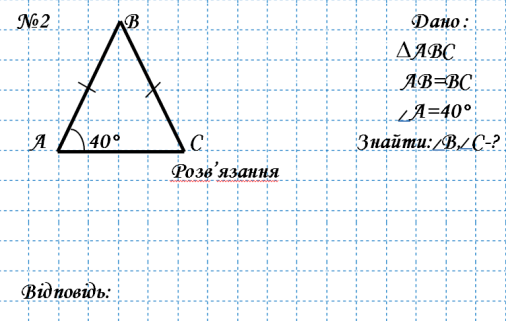





ПІБ учня______________
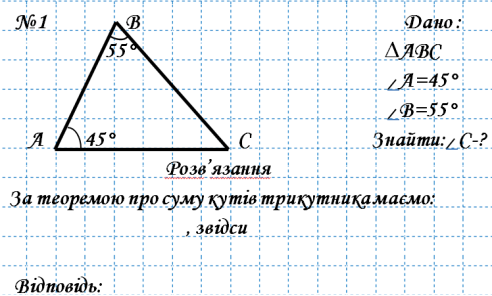
1.Чи може сума кутів трикутника дорівнювати 2000 ?
- Так О ні
2. Чи існує трикутник з двома прямими кутами?
- Так О ні
3.Чи існує трикутник з кутами 600, 500, 700?
- Так О ні
4. Сума двох кутів трикутника дорівнює 1400. Знайдіть третій кут.
- 40°
- 180°
- 140°
- 90°
5. Один кут у трикутнику прямий. Якими є два інші кути?
- Прямі
- Розгорнуті
- Тупі
- Гострі
6. Знайдіть третій кут трикутника, якщо два його кути дорівнюють
400 і 600.
- 40°
- 60°
- 80°
- 100°
7. У трикутнику ABC A= 600 , B= 800. Який це трикутник?
- Гострокутний
- Прямокутний
- Тупокутний
8. 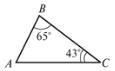 9.
9. 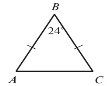
Знайдіть кутА Знайдіть кути А і С
- 65° О 24° 24°
- 43° О 90° 24°
- 72° О 76° 76°
- 90° О 78° 78°
10. Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.
- 72°
- 36°
- 43°
- 90°
ПІБ учня______________
1. Сума двох кутів трикутника дорівнює 1400. Знайдіть третій кут.
- 90°
- 140°
- 180°
- 40°
2. Чи існує трикутник з двома прямими кутами?
- Так О ні
3. Знайдіть третій кут трикутника, якщо два його кути дорівнюють
400 і 600.
- 80°
- 60°
- 40°
- 100°
4.  5.
5. 
Знайдіть кутА Знайдіть кути А і С
- 72° О 76° 76°
- 43° О 90° 24°
- 65° О 24° 24°
- 90° О 78° 78°
6.Чи існує трикутник з кутами 600, 500, 700?
- Так О ні
7.Чи може сума кутів трикутника дорівнювати 2000 ?
- Так О ні
8. Один кут у трикутнику прямий. Якими є два інші кути?
- Прямі
- Розгорнуті
- Тупі
- Гострі
9. Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.
- 43°
- 90°
- 72°
- 36°
10. У трикутнику ABC A= 600 , B= 800. Який це трикутник?
- Гострокутний
- Тупокутний
- Прямокутний

![]()
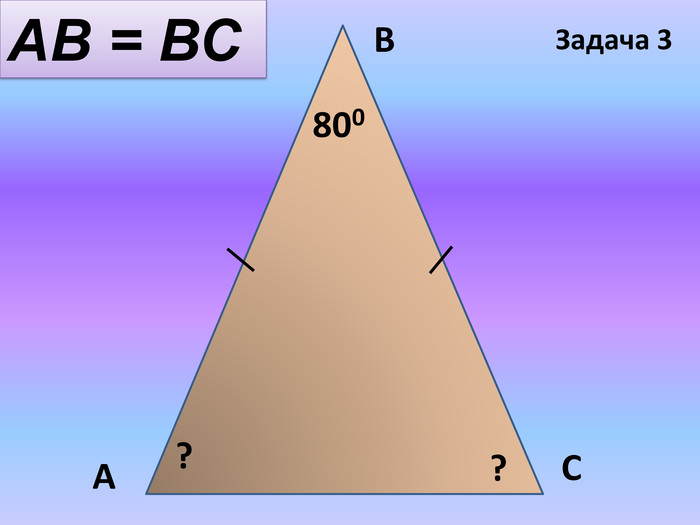
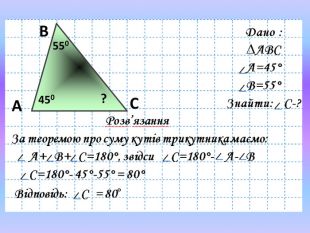
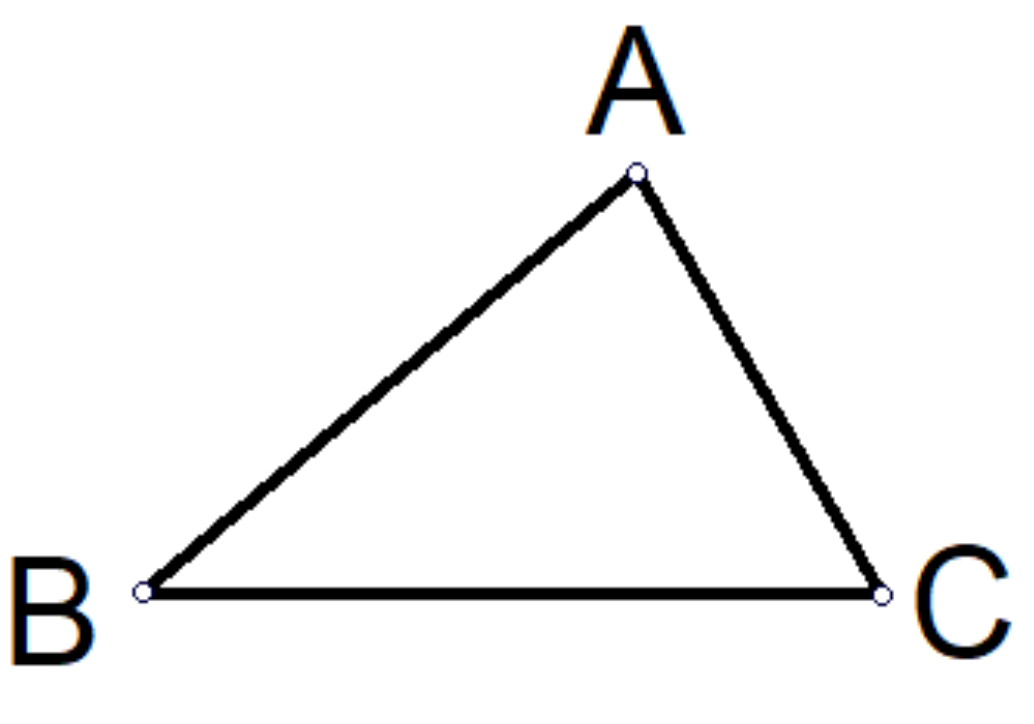
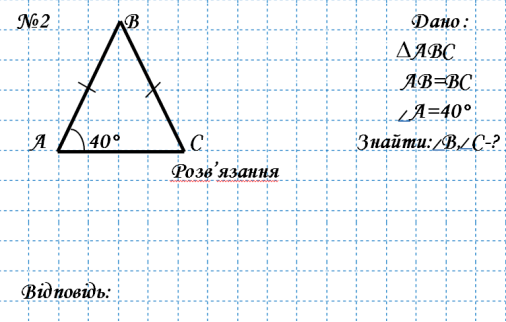
![]() №2 В Дано :
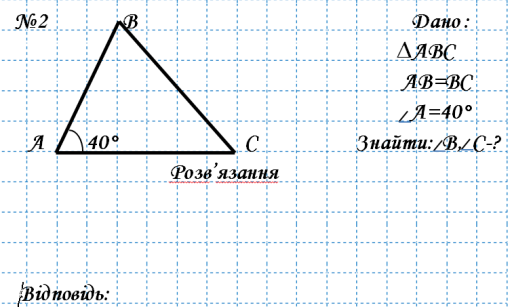
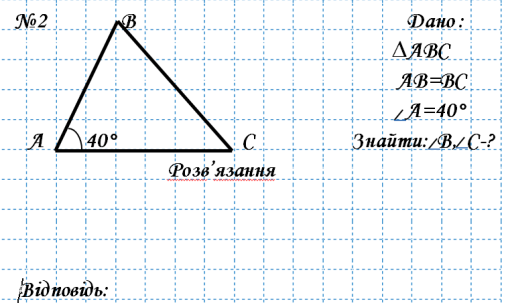
№2 В Дано :
∆АВС
![]()
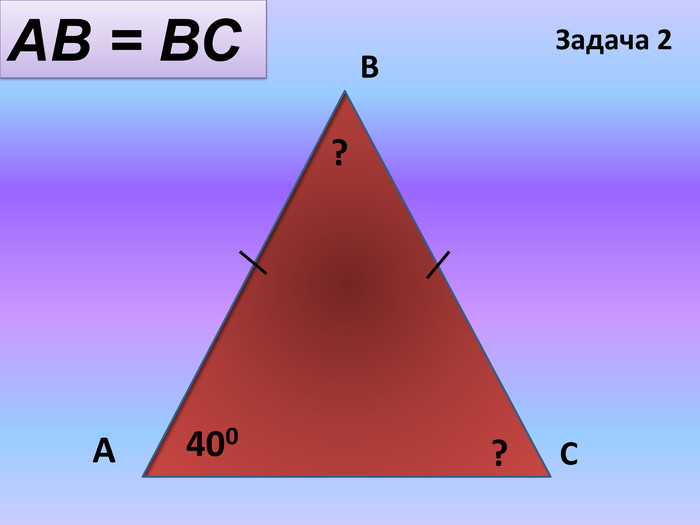
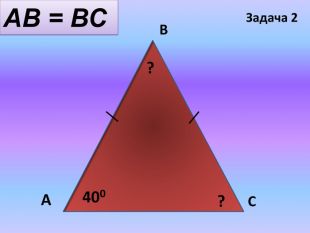
![]() АВ=ВС
АВ=ВС
![]() А=40°
А=40°
![]()
![]()
![]()
![]() А 40° С Знайти: В, С-?
А 40° С Знайти: В, С-?
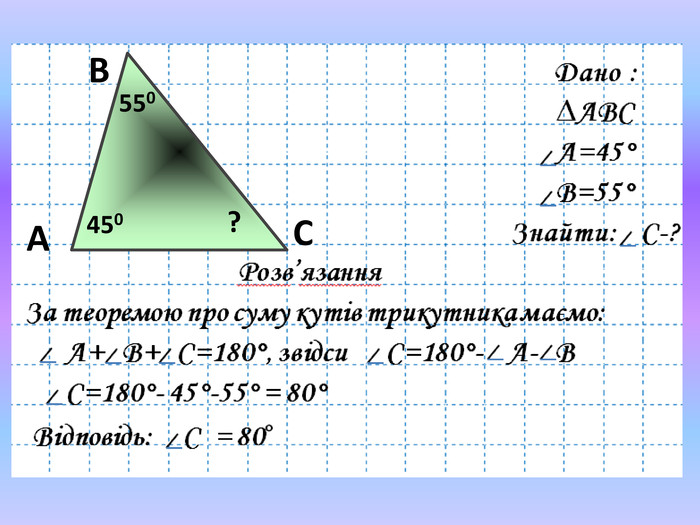
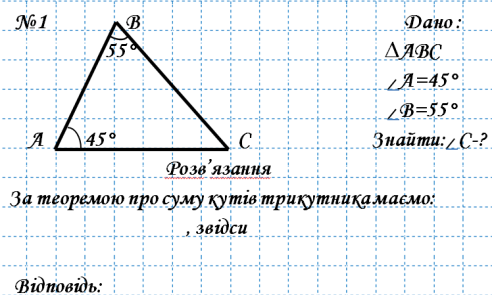
Розв’язання
Відповідь:
|
|
= |
|
|
= |
|
|
= |
|
|
|

Урок математики у 7-му класі Мальована Н.В.
Тема уроку. «Сума кутів трикутника».
Мета уроку:
Навчальна:
створити умови для сприйняття, осмислення і первинного закріплення блоку нової навчальної інформації по темі «Сума кутів трикутника».
- формувати практичні навички застосування знань про властивості трикутника при розв’язуванні завдань з життєвим навантаженням;
- узагальнити знання про трикутник, вивчити, осмислити і вміти застосовувати теорему про суму кутів трикутника, розширити знання про різновиди трикутників.
- підвищити мотивацію до вивчення теми «Сума кутів трикутника»;
- знати теорему про суму кутів трикутника, вміти застосовувати її під час вирішення завдань, свідомо обирати найбільш ефективні шляхи вирішення, розвивати вміння працювати з навчальним текстом, проводити класифікацію трикутників в залежності від їх кутів.
- усвідомити цінність знань для повсякденного життя;
- формувати ключові, предметні і міжпредметні компетентності.
Розвивальна:
- розвивати логічне мислення, монологічне і діалогічне математичне мовлення, аналітичні уміння і навички (класифікувати, аналізувати, мислити чітко, генерувати альтернативні рішення, переконувати).
Виховна:
- виховувати: працьовитість, креативність, ініціативність, активність, вольові якості, цілеспрямованість, впевненість в собі, конкурентоспроможність, самостійність у прийнятті рішень в умовах невизначеності.
Ключові компетентності, які формуються на уроці
Ціннісно-смислові:
- формулювати свої ціннісні орієнтири по відношенню до навчального предмету та сфери діяльності, володіти способами самовизначення в ситуації вибору на основі власних позицій;
- уміти приймати рішення, брати на себе відповідальність за наслідки, здійснювати дії та вчинки на основі обраних цільових установ.
Навчально-пізнавальні:
- ставити мету і організовувати її досягнення, уміти пояснити мету;
- організовувати планування, аналіз, рефлексію, самооцінку своєї пізнавальної діяльності;
- ставити пізнавальні задачі і знаходити їх розв’язання;
- володіти вимірювальними навичками, працювати з інструментами, діловими паперами;
- описувати результати, формулювати висновки; розповідати усно чи письмово про результати свого дослідження з використанням мультимедійних засобів.
Соціокультурні:
- володіти знаннями і досвідом виконання соціальних ролей працівника, власника; уміти діяти в щоденних ситуаціях сімейно-побутової сфери;
Комунікативні:
- володіти способами взаємодії; уміти задавати питання, коректно вести навчальний діалог;
- володіти різними способами діяльності в групі; прийомами дії в ситуаціях спілкування, умінням шукати і знаходити компроміси.
Інформаційні:
- самостійно шукати, систематизувати, аналізувати і відбирати необхідну інформацію для вирішення навчальної задачі;
- орієнтуватись в інформаційному просторі, усвідомлено сприймати інформацію;
- володіти навичками роботи з комп’ютером, телефоном.
Здоров’язберігаючі:
- володіти способами емоційної саморегуляції, підтримки і самоконтролю.
Тип уроку. Урок когнітивного типу; урок постановки проблем і їх рішень за Case - технологією з використанням методів аналізу – методу ситуативного аналізу (Case-study) .
Вид кейсу. Навчальний.
Обладнання: мультимедійний проектор, кейси учнів, висловлювання видатних людей про математику.
Хід уроку
І. Вступне слово вчителя.
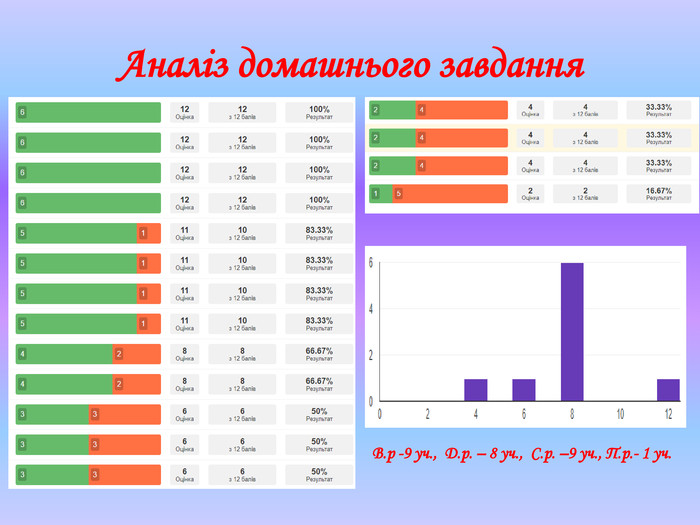
ІІ. Перевірка домашнього завдання
Аналіз виконання домашнього завдання на тестовій платформі «На урок»
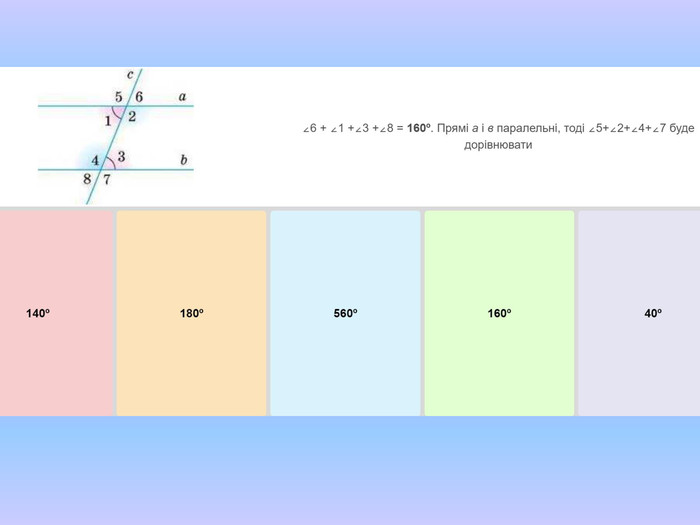
ІІІ. Актуалізація опорних знань.
https://learningapps.org/5599490
ІV. Мотивація навчальної діяльності учнів
Діти, а скажіть будь-ласка вивченню якої фігури ми приділяємо найбільше уваги в 7 класі?
Хоч трикутник і найпростіший з вигляду багатокутник, але за кількістю властивостей він випереджає багато інших геометричних фігур.
З трикутниками ми зустрічаємось досить часто : вітрило корабля, повітряний змій, дах будинку і т. д. – все це трикутники. Мабуть, це найголовніша фігура, бо з трикутників, як з цеглинок, складаються майже всі геометричні фігури, які ми будемо вивчати далі.
Вчитель опитує методом «незакінченого речення»
1) Рівнобедреним називається трикутник…( у якого дві сторони рівні.)
2) Різностороннім називається трикутник…( у якого всі сторони мають різну довжину)
3) Якщо у трикутника всі кути рівні…( то він рівносторонній)
4) Гострий кут – це…(кут менше 90˚)
5) Прямий кут _ це …
6. Тупий кут-…
7. Розгорнутий - …
V. Засвоєння нових знань
Зміст практичного кейсу 1
Учитель: Зараз я хочу запропонувати вам виступити в ролі дослідників і зробити математичне обґрунтування своїх спостережень і припущень. Може бути, у вас і не вийде зробити ніяких нових відкриттів в області геометрії, але кожен з вас побуває в ролі першовідкривача, якщо буде уважним і спостережливим.
Завдання групам: шляхом дослідження висунути гіпотезу про суму кутів трикутника.
Група перша.
- Будуйте трикутник з двома прямими кутами.
А = 90 0
В = 30 0
С = 90 0
Група друга
- Будуйте трикутник з двома тупими кутами.
А = 120 0
В = 50 0
С = 100 0
Третя група
- Будуйте трикутник з тупим і прямим кутом.
А = 120 0
В = 30 0
С = 90 0
Запитання до класу:
Чи завжди можна побудувати трикутник за даними кутами?
Якими повинні бути кути трикутника, щоб він існував?
Отже, тема нашого уроку «Сума кутів трикутника» і мета знати і вміти доводити теорему про суму кутів трикутника, вміти застосовувати її під час розв’язування задач.
Зміст практичного кейсу 2
![]()

![]()
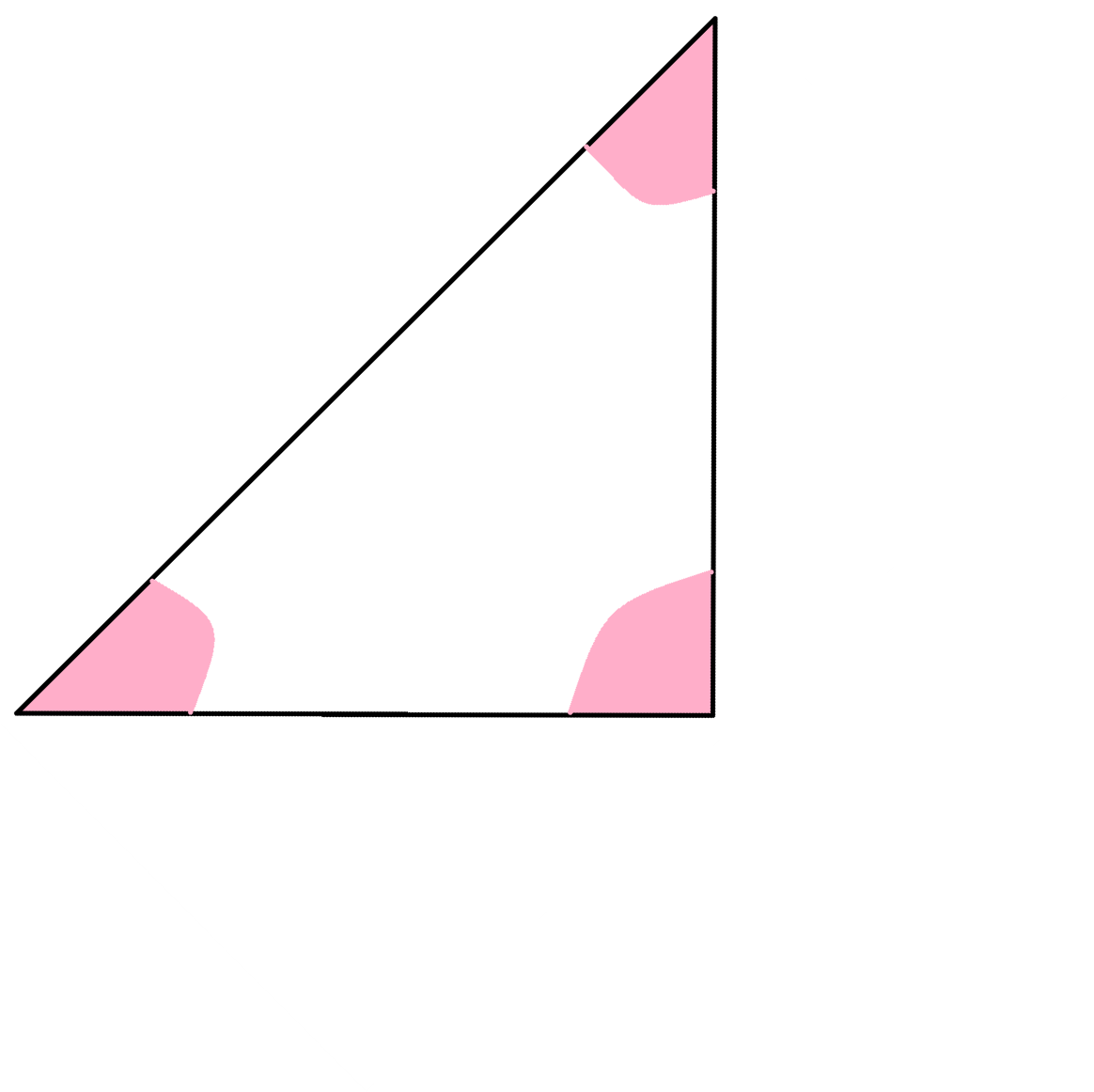
![]() Завдання 1 групі: Шляхом перегинання отримати прямокутник і зробити висновок про суму кутів трикутника.
Завдання 1 групі: Шляхом перегинання отримати прямокутник і зробити висновок про суму кутів трикутника.
Завдання 2 групі. На парті три трикутника різних видів гострокутий, прямокутний, тупокутний. Розрізати трикутники на три частини, щоб вийшло три кути. Спробувати визначити їх суму. Зробити висновок.
Учні роблять висновок: отримані три кути утворюють розгорнутий кут. Завдання 3 групі. На картках побудований трикутники. Виміряти кути кожного трикутника за допомогою транспортира. Дані вимірювань занести в таблицю. Зробіть висновок про суму кутів трикутника.
Після закінчення роботи кожна група представляє свої результати. За результатами доходимо висновку, що сума кутів близька до 180°, а периметр різний у всіх трикутників.
При виконанні даної роботи в учнів формується наочне представленя про суму кутів трикутника.
Учитель: Чи можемо ми стверджувати, що сума кутів будь-якого трикутника дорівнює 180˚? Або це випадковий збіг?
(Демонстрація сума кутів трикутника в пакеті DG)
Те, що сума кутів трикутника дорівнює 180 , було відомо в стародавньому Єгипті, проте доведено було значно пізніше. Вважають, що теорему про суму кутів трикутника довів Піфагор
(VІ ст. до н. е.)
Доведення теореми
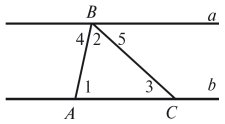
Зміст теоретичного кейсу 3
|
Сума кутів трикутника |
|
|
Теорема |
|
|
|
Сума кутів трикутника дорівнює 180°. |
|
Висновки |
|
|
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі |
|
VІ. Первинне усвідомлення нового матеріалу
Зміст практичного кейсу 4
VІІ. Підсумок уроку .
ПІБ учня______________
1.Чи може сума кутів трикутника дорівнювати 2000 ?
- Так О ні
2. Чи існує трикутник з двома прямими кутами?
- Так О ні
3.Чи існує трикутник з кутами 600, 500, 700?
- Так О ні
4. Сума двох кутів трикутника дорівнює 1400. Знайдіть третій кут.
- 40°
- 180°
- 140°
- 90°
5. Один кут у трикутнику прямий. Якими є два інші кути?
- Прямі
- Розгорнуті
- Тупі
- Гострі
6. Знайдіть третій кут трикутника, якщо два його кути дорівнюють 400 і 600.
- 40°
- 60°
- 80°
- 100°
7. У трикутнику ABC A= 600 , B= 800. Який це трикутник?
- Гострокутний
- Прямокутний
- Тупокутний
8. 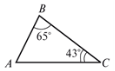 9.
9. 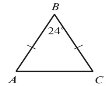
Знайдіть кутА Знайдіть кути А і С
- 65° О 24° 24°
- 43° О 90° 24°
- 72° О 76° 76°
- 90° О 78° 78°
10. Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.
- 72°
- 36°
- 43°
- 90°
VІІІ. Домашнє завдання.
Опрацювати §16 ст.124,
вивчити теорему 16.1.,
розв’язати №359, 373(вис.р),
онлайн-тест 79416899.
ІХ. «Рефлексія»
-
 - все зрозумів / зрозуміла
- все зрозумів / зрозуміла
- - майже все зрозумів / зрозуміла
- - нічого не зрозумів / не зрозуміла
1


про публікацію авторської розробки
Додати розробку