Співвідношення між тригонометричними функціями одного аргументу.
Тема .Співвідношення між тригонометричними функціями одного аргументу.
Мета: повторити, систематизувати та поглибити знання, вміти перетворювати тригонометричні вирази;
формувати навички творчого застосування знань до виконання вправ ;
виховувати культуру ведення записів як на дошці, так і в зошитах.
- 1 відповідь.doc doc
- ВИКОРИСТОВУВАТИ.doc doc
- ЗРОЗУМІВ.doc doc
- робота 1.doc doc
- Показати всі файли


БУДУ ВИКОРИСТОВУВАТИ

НЕ ЗРОЗУМІВ
Самостійна робота № 1
- Які трикутники називаються прямокутними?
А) у якого один кут =900 Б) у якого два кути =900 В) у якого всі кути =900
2. Який вчений вивів основну теорему про прямокутні трикутники?
А) Архімед Б) Піфагор В)Фалес
3. Як можна записати у вигляді формули основну теорему про прямокутні трикутники?
А) а2*b2=r2 Б) а2 - b2 =с2 В) а2 + b2 =с2
4. Що називається sinα (синусом) кута α?
А) відношення абсциси до хорди кола Б) відношення абсциси до ординати В) відношення ординати до
довжини радіуса
5. Що називається cosα (косинусом) кута α?
А) відношення ординати до хорди кола Б) відношення ординати до довжини В) відношення ординати
радіуса до абсциси
6. Що називається tgα (тангенсом) кута α?
А) відношення ординати до абсциси В) відношення катета до довжини Б) відношення хорди кола до
радіуса ординати
![]()
Самостійна робота № 1
- Які трикутники називаються прямокутними?
А) у якого один кут =900 Б) у якого два кути =900 В) у якого всі кути =900
2. Який вчений вивів основну теорему про прямокутні трикутники?
А) Архімед Б) Піфагор В)Фалес
3. Як можна записати у вигляді формули основну теорему про прямокутні трикутники?
А) а2*b2=r2 Б) а2 - b2 =с2 В) а2 + b2 =с2
4. Що називається sinα (синусом) кута α?
А) відношення абсциси до хорди кола Б) відношення абсциси до ординати В) відношення ординати до
довжини радіуса
5. Що називається cosα (косинусом) кута α?
А) відношення ординати до хорди кола Б) відношення ординати до довжини В) відношення ординати
радіуса до абсциси
6. Що називається tgα (тангенсом) кута α?
А) відношення ординати до абсциси В) відношення катета до довжини Б) відношення хорди кола до
радіуса ординати
![]()
Самостійна робота № 1
- Які трикутники називаються прямокутними?
А) у якого один кут =900 Б) у якого два кути =900 В) у якого всі кути =900
2. Який вчений вивів основну теорему про прямокутні трикутники?
А) Архімед Б) Піфагор В)Фалес
3. Як можна записати у вигляді формули основну теорему про прямокутні трикутники?
А) а2*b2=r2 Б) а2 - b2 =с2 В) а2 + b2 =с2
4. Що називається sinα (синусом) кута α?
А) відношення абсциси до хорди кола Б) відношення абсциси до ординати В) відношення ординати до
довжини радіуса
5. Що називається cosα (косинусом) кута α?
А) відношення ординати до хорди кола Б) відношення ординати до довжини В) відношення ординати
радіуса до абсциси
6. Що називається tgα (тангенсом) кута α?
А) відношення ординати до абсциси В) відношення катета до довжини Б) відношення хорди кола до
радіуса ординати
Самостійна робота № 2
- Який вигляд має ОСНОВНА ТРИГОНОМЕТРИЧНА ТОТОЖНІСТЬ?
А) tgα*ctgα=1 Б) sin2α*cos2α=1 В) sin2α-cos2α=1 Г) sin2α+cos2α=1
- Чому дорівнює добуток tgα*ctgα?
А) ![]() Б) 1,5 В) 1 Г) sin2α
Б) 1,5 В) 1 Г) sin2α
-
Що треба вставити в формулу замість … щоб отримати вірну тотожність
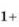 …
… 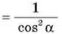 ?
?
А) sin2α Б) tg2α В)![]() Г) ctg2α
Г) ctg2α
- Чому дорівнює cosα виходячи з ОСНОВНОЇ ТРИГОНОМЕТРИЧНЩЇ ТОТОЖНІСТІ?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
-
Спростіть вираз
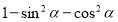
А) - sin2α Б) 0 В) 2 Г) ![]()
- Як називаються функціїї у= sinх, у = cosх?
А) Логарифмічні Б) Квадратичні В) Тригонометричні Г) Обернені
![]()
Самостійна робота № 2
- Який вигляд має ОСНОВНА ТРИГОНОМЕТРИЧНА ТОТОЖНІСТЬ?
А) tgα*ctgα=1 Б) sin2α*cos2α=1 В) sin2α-cos2α=1 Г) sin2α+cos2α=1
- Чому дорівнює добуток tgα*ctgα?
А) ![]() Б) 1,5 В) 1 Г) sin2α
Б) 1,5 В) 1 Г) sin2α
-
Що треба вставити в формулу замість … щоб отримати вірну тотожність
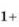 …
… 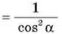 ?
?
А) sin2α Б) tg2α В)![]() Г) ctg2α
Г) ctg2α
- Чому дорівнює cosα виходячи з ОСНОВНОЇ ТРИГОНОМЕТРИЧНЩЇ ТОТОЖНІСТІ?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
-
Спростіть вираз
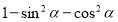
А) - sin2α Б) 0 В) 2 Г) ![]()
- Як називаються функціїї у= sinх, у = cosх?
А) Логарифмічні Б) Квадратичні В) Тригонометричні Г) Обернені
![]()
Самостійна робота № 2
- Який вигляд має ОСНОВНА ТРИГОНОМЕТРИЧНА ТОТОЖНІСТЬ?
А) tgα*ctgα=1 Б) sin2α*cos2α=1 В) sin2α-cos2α=1 Г) sin2α+cos2α=1
- Чому дорівнює добуток tgα*ctgα?
А) ![]() Б) 1,5 В) 1 Г) sin2α
Б) 1,5 В) 1 Г) sin2α
-
Що треба вставити в формулу замість … щоб отримати вірну тотожність
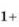 …
… 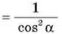 ?
?
А) sin2α Б) tg2α В)![]() Г) ctg2α
Г) ctg2α
- Чому дорівнює cosα виходячи з ОСНОВНОЇ ТРИГОНОМЕТРИЧНЩЇ ТОТОЖНІСТІ?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
-
Спростіть вираз
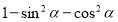
А) - sin2α Б) 0 В) 2 Г) ![]()
- Як називаються функціїї у= sinх, у = cosх?
А) Логарифмічні Б) Квадратичні В) Тригонометричні Г) Обернені
Тема .Співвідношення між тригонометричними функціями
одного аргументу.
Мета: повторити, систематизувати та поглибити знання, вміти перетворювати тригонометричні вирази;
формувати навички творчого застосування знань до виконання вправ ;
виховувати культуру ведення записів як на дошці, так і в зошитах.
Тип уроку: комбінований
Форми роботи: колективна, групова, індивідуальна.
Методи навчання: пояснювально-ілюстративний, продуктивно-практичний.
Обладнання: відео фрагмент, опорний конспект, роздатковий матеріал, підручники.
ХІД УРОКУ
І. Організаційний етап.
ІІ. Актуалізація опорних знань.
Давайте згадаємо матеріал попереднього уроку і знання які Ви отримали з курсу алгебри та геометрії в 8-9 класах.
Самостійна робота
- Які трикутники називаються прямокутними?
А) у якого один кут =900 Б) у якого два кути =900 В) у якого всі кути =900
2. Який вчений вивів основну теорему про прямокутні трикутники?
А) Архімед Б) Піфагор В)Фалес
3. Як можна записати у вигляді формули основну теорему про прямокутні трикутники?
А) а2*b2=r2 Б) а2 - b2 =с2 В) а2 + b2 =с2
4. Що називається sin α (синусом) кута α?
А) відношення абсциси до хорди кола Б) відношення абсциси до ординати В) відношення ординати до
довжини радіуса
5. Що називається cos α (косинусом) кута α?
А) відношення ординати до хорди кола Б) відношення ординати до довжини В) відношення ординати
радіуса до абсциси
5. Що називається tg α (тангенсом) кута α?
А) відношення ординати до абсциси Б) відношення катета до довжини В) відношення хорди кола до
 радіуса ординати
радіуса ординати
Відповіді заносять на картинку «СМАЙЛИК»
IІI. Формулювання теми, мети і завдань уроку
Демонстрація відео фрагменту 
Тригонометрія (від грец. τρίγονο — трикутник та μετρειν — вимірюю, тобто буквально вимірювання трикутників)
Коротке повідомлення учня (Зародження тригонометрії)
Тригонометрія зустрічається не лише в математиці, але хто би міг подумати, і в фізиці, астрономії, медицині, інших галузях:
- пружинний маятник;
- поява веселки (закон заломлення)
- одним з основних властивостей живої природи є біоритм. Модель біоритмів може бути побудована з використанням тригонометричних функцій. Для побудови моделі біоритмів необхідно ввести дату народження людини, дату відліку (день, місяць, рік) і кількість днів);
- якщо на хвості риби зафіксувати точку, то можна розглянути траекторію руху, яка нагадує косинусоїду чи синусоїду. А при плаванні тіло риби приймає форму кривої, яка нагадує графік функції y=tg x;
- при польоті птахів траєкторія взмаху крил утворює синусоїду;
- в архітектурі: ресторан в Лос-Манантіалісі, Виноробня «Бодегас Ісіос», дитяча школа в Барселоні, страхова корпорація в Лондоні;
- на танцях інколи є таких рух як хвиля, що також нагадує синусоїду чи косинусоїду.
Коротке повідомлення учня (Межі застосування тригонометрії)
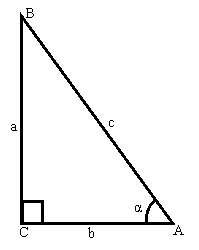 Згадаємо що:
Згадаємо що:
sin α=a/с
cos α=b/c
tg α=a/b
ctg α=b/c
Згадаємо Т. Піфагора
а2+ b2=с2
Коротке повідомлення учня (Науковий внесок Піфагора)
Зобразимо в системі координат одиничне коло і на колі візьмемо т. А(х;у)
І розглянемо трикутник АОВ то:
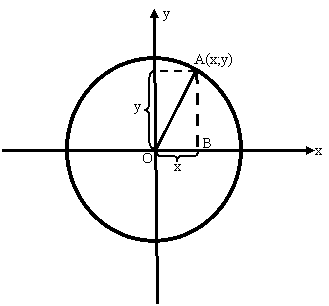 sin α=у/r
sin α=у/r
cos α=x/r
tg α=y/x
ctg α=x/y
Коротке повідомлення учня ( Звідки взялись назви синус, косинус і тангенс)
Тепер перепишемо Теорему Піфагора стосовно нашого трикутника АОВ, ми отримаємо
х2+у2= r2
Поділимо отримане рівняння на r2
х2/ r2+у2/ r2= r2/ r2 , шляхом елементарних перетворень отримаємо
х2/ r2+у2/ r2=1 , замінимо отримані частки відповідно на sin2α та cos2α отримаємо
sin2α+cos2α=1 *
ОСНОВНА ТРИГОНОМЕТРИЧНА ТОТОЖНІСТЬ
sin2α+cos2α=1 перенесемо sin2α в протилежну сторону рівняння з протилежним знаком, отримаємо
cos2α=1-sin2α позбудимось квадрате біля косинусу, отримаємо
![]() **
**
Аналогічно отримаємо
![]() ***
***
З означення tgα і ctgα виведемо
![]() ****
****
і ![]() *****
*****
Перемножимо
tgα*ctgα= ![]() *
*![]() =1
=1
tgα*ctgα=1 ******
Візьмемо знову основну тригонометричну тотожність
sin2α+cos2α=1 і поділимо обидві частини рівняння на sin2α, отримаємо
sin2α /sin2α +cos2α/ sin2α =1/ sin2α
![]() *******
*******
Аналогічно отримаємо
![]() ********
********
А зараз прочитайте в підручнику §16 ст. 98, «Математика-10» Бурда М.І. і особливо зверніть увагу на розв’язані приклади 1-4 у підручнику.
IV . Закріплення знань і навичок.
Розв’язування завдань з підручника «Математика-10» Бурда М.І. ст. 101,
№211, №213, №214, №217, №223
Самостійна робота № 2
- Який вигляд має ОСНОВНА ТРИГОНОМЕТРИЧНА ТОТОЖНІСТЬ?
А) tgα*ctgα=1 Б) sin2α*cos2α=1 В) sin2α-cos2α=1 Г) sin2α+cos2α=1
- Чому дорівнює добуток tgα*ctgα?
А) ![]() Б) 1,5 В) 1 Г) sin2α
Б) 1,5 В) 1 Г) sin2α
-
Що треба вставити в формулу замість … щоб отримати вірну тотожність
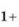 …
… 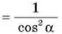 ?
?
А) sin2α Б) tg2α В)![]() Г) ctg2α
Г) ctg2α
- Чому дорівнює cos α виходячи з ОСНОВНОЇ ТРИГОНОМЕТРИЧНЩЇ ТОТОЖНІСТІ?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
-
Спростіть вираз
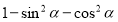
А) - sin2α Б) 0 В) 2 Г) ![]()
-
 Як називаються функціїї у= sin х, у = cos х?
Як називаються функціїї у= sin х, у = cos х?
А) Логарифмічні Б) Квадратичні В) Тригонометричні Г) Обернені
Відповіді заносяться в таблицю.
V. Підведення підсумків виставлення оцінок домашнє завдання
§16 ст. 98, «Математика-10» Бурда М.І. ст. 101 № 212, №215, №218
VІ . Рефлексія
Вчитель приклеює на дошку три картинки з зображеннями «Буду використовувати», «Зрозумів», «Не зрозумів»
 і учні за допомогою «Стікерів», приклеюють «Стікери» проти тієї картинки, що їм до вподоби
і учні за допомогою «Стікерів», приклеюють «Стікери» проти тієї картинки, що їм до вподоби



1
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Клас _____________________ Прізвище та Ім'я |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
А |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|














про публікацію авторської розробки
Додати розробку
