Способи доведення основних числових нерівностей.

Способи доведення основних числових нерівностей.

 

З способами доведення теорем учні знайомляться в 7 класі. Новою програмою не передбачається вивчення окремої теми «Доведення нерівностей», але завдання з цієї теми часто зустрічаються на олімпіадах і слугують гарним засобом розвитку логічного мислення та формування евристичних прийомів розв’язування задач. Також цю тему вивчають у класах з поглибленим вивченням математики. Розглянемо деякі способи доведення .

 

1.               Синтетичний і аналітичний методи доведення.

Розглянемо доведення такого твердження:

Приклад

Якщо а > 0 і b > 0, то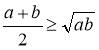

Доведення

Якщо а > 0 і b > 0 , то або а - 2 + b ≥ 0,

Звідки а + b ≥ 2.

Поділивши обидві частини на 2, дістанемо

,

Що й треба було довести.

Нерівність 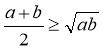називають нерівністю Коші для двох чисел.

Логічною основою в цьому доведенні є аксіома, що з правиль­ного твердження завжди випливає і правильний наслідок. Мірку­вання в ньому йдуть від умови і вже відомого твердження до доводжуваного. Такий метод   доведення   називають синтетичним.

Синтетичний метод доведення дуже простий з логічного погляду, такі доведення найбільш переконливі і порівняно короткі. Тому більшість теорем у шкільному курсі математики доводять синте­тичним методом.

Але такі доведення не позбавлені і деяких недоліків. Як дога­датися, що доведення наведеного вище твердження треба починати з  нерівності   Як   догадатися,  в якому   напрямі треба виконувати перетворення написаної нерівності, щоб дістати бажаний результат? Синтетичний метод доведення зручний тоді, коли доведення уже відоме і ми хочемо пояснити його іншим. Якщо ж відшукуємо доведення, то зручніша користуватись аналі­тичним методом.

Аналітичним називають такий метод доведення, при якому міркування йдуть від доводжуваного твердження до відо­мих, від тези до аргументів.

 

Приклад.

Доведемо ту саму нерівність аналітичним методом.

 

Доведення

Щоб показати, що при а > 0 і b > 0

досить  показати,  що

а + b ≥ 2

бо з цієї нерівності випливає доводжувана. Нерівність   (2) випли­ває  з такої:

а - 2 + b ≥ 0,

або .

Ця нерівність правильна при будь-яких додатних а і b, бо квадрат дійсного числа не може бути від'ємним.

Отже, доводжувана нерівність правильна, оскільки випливає з правильного твердження.

Логічна основа аналітичного методу доведення така сама, як і синтетичного: з правильного твердження завжди випливає правиль­ний наслідок. Відрізняється він від синтетичного тільки напрямом міркувань. При доведенні аналітичним методом спочатку підшукують таке твердження, з якого випливає доводжуване, потім таке, з якого випливає підшукане раніше, і т. д. доти, доки не при­ходять до вже відомого твердження. Цей напрям міркувань проти­лежний тому,  який маємо ,при синтетичному методі.

Зауважимо, що іноді аналітичним методом доведення нази­вають зовсім інший спосіб міркувань, суть якого сформулював ще Евклід (тому його називають аналізом Евкліда): «Твер­дження доводять аналітично, якщо шукане приймають за відоме і на основі виведених звідси наслідків дістають відому істину». Застосуємо такий спосіб міркувань до доведення вже відомої нам нерівності.

Припустимо, що нерівність (а > 0, b > 0) правильна. Помножимо обидві її частини на 2:

а + b ≥ 2.

Перенесемо 2 в ліву частину:

а - 2 + b ≥ 0,    .

Остання нерівність правильна, бо квадрат дійсного числа не може бути  від'ємним.   Отже,   правильна і доводжувана нерівність.

Такі міркування не можна вважати строгими доведеннями. Тут показано, що з доводжуваного твердження випливає правильний наслідок. А це ще не означає, що доводжуване правильне, бо пра­вильний наслідок можна дістати і з неправильного твердження. Наприклад, рівність -2 = 2 неправильна, проте, підносячи оби­дві її частини до квадрата,  дістанемо правильну рівність 4 = 4.

Отже, аналіз Евкліда не можна вважати строгим методом дове­дення. Проте його зручно застосовувати для знаходження ще не відомого доведення, а оформляти саме доведення краще синтетич­ним методом.

 

2.               Метод доведення від супротивного.

Як відомо, для супротивних тверджень справджується закон виключеного третього: з двох супротивних тверджень одне завжди правильне, друге — ні, а третього бути не може. Тому замість безпосереднього доведення даного твердження можна показати, що супротивне йому твердження неправильне. З цього випливатиме справедливість даного.

Метод доведення, логічною основою якого є закон виключення третього, називають методом доведення від супротивного.

Методом від супротивного часто користуються в геометрії, особливо при доведенні теорем з перших параграфів планіметрії і стереометрії. Нерідко використовують його і  при доведенні алгебраїчних тверджень.

Доведемо цим методом, наприклад, таку нерівність:

 

Приклад.

Для будь-яких значень а₁, а₂, b₁, b₂ доведіть нерівність

(а₁ b_{1 +} а₂ b₂)² ≤ (а₁²+ а₂ ²)( b₁² + b₂²)  (*)

Доведення

Нехай нерівність, що доводиться, є неправильною. Тоді знайдуться такі числа а₁, а₂, b₁, b₂, що буде правильною нерівність

(а₁ b_{1 +} а₂ b₂)² > (а₁²+ а₂ ²)( b₁² + b₂²).

Звідси:

а₁² b₁² + 2 а₁ b₁ а₂ b₂ + а₂ ² b₂² > а₁² b₁² + а₁² b₂² + а₂ ² b₁² + а₂ ² b₂² ;

2 а₁ b₁ а₂ b₂ > а₁² b₂² + а₂ ² b₁²;

а₁² b₂² - 2 а₁ b₁ а₂ b₂ + а₂ ² b₁² < 0;

(а₁ b₂ - а₂ b₁)² < 0.

Остання нерівність є неправильною. Отримана суперечність означає, що нерівність (*) є правильною.

Нерівність (*) є окремим випадком більш загальної нерівності

(а₁b₁ + а₂b₂ + …+ а_nb_n) ≤ (а₁² + а₂²+…+ а_n²)(b₁² + b₂²+…+b_n²).(**)

Нерівність (**) називають нерівністю Коші-Буняковського.

 

Приклад

Доведемо тепер методом від супротивного нерівність:

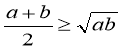( а > 0, b > 0).

Доведення

Припустимо,   що  при  деяких   а > 0  і   b > 0 .    Тоді    a + b < 2 ,   а - 2 + b < 0,   . Остання нерівність не може бути правильною ні при яких додатних а і b. Отже, припущення неправильне. Тому при всіх додатних а і b

.

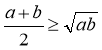Щоб успішно користуватись методом від супротивного, треба вміти заперечувати різні висловлення, в тому числі і висловлення із кванторами. Спостереження показують, що при цьому учні нерідко допус­кають помилки. Так, заперечуючи висловлення «при всіх додатних а і b  а + b ≥ 2 », учні нерідко пишуть «при всіх додатних а і b a+ b < 2 ». Це висловлення не є запереченням першого, бо замість слова «всіх» тут треба написати «деяких», адже

і .

Зрозуміло, що у школі оперувати подібними записами не слід. Однак на конкретних прикладах учням треба показати, що, запе­речуючи висловлення з словом «всіх», останнє замінюємо словом «деяких» і навпаки. Можна запропонувати учням проаналізувати, наприклад, і таке «доведення» методом від супротивного:

«Довести, що при всіх додатних а і b .

Доведення.

Припустимо, що при всіх додатних а і b . Це припущення неправильне, бо, наприклад, неправильною є нерівність . Отже, правильною є доводжувана нерівність».

Де тут помилка? У спростуванні припущення? Ні, бо щоб спростувати висловлення «при всіх додатних а і b », досить навести один приклад. Помилку допущено в запереченні. У ньому слово «всіх» треба замінити на «деяких».

Примітка. У сучасній математиці існує окремий напрям — інтуїціонізм, прихильники якого не визнають закону виключеного третього, а отже, не користуються методом доведення від супротивного. Пояснюють це тим, що застосування цього закону в теорії нескінченних множин призводить до суперечностей. Що ж до предметів, які вивчаються в шкільній математиці, то для них закон виключеного третього завжди виконується. Отже, у школі доведення методом від супротивного завжди допустимі; вони такі самі строгі, як і інші доведення, не зв'язані з законом виключеного третього.

 

3.               Метод математичної індукції

Логічною основою цього методу доведення є така аксіома: Якщо твердження, формулювання якого містить змінну п, правильне при п =1 і якщо з припущення, що воно правильне при довільному п = k, випливає, що воно правильне і при п == k + 1, то це твердження правильне при всіх натуральних значеннях п.

Методом математичної індукції можна доводити не тільки ті твердження, які правильні при п = 1, а й такі, які правильні для всіх натуральних п, більших від деякого р. У цьому випадку можна спочатку зробити заміну п = m + р і доводити індукцією по m, а можна посилатись на такий наслідок з аксіоми індукції.

Якщо твердження із змінною п правильне при п = р і якщо з припущення, що воно правильне при п = k, де k > p, випливає, що воно правильне при п=k+1, то це твердження правильне при всіх цілих значеннях п ≥ p. (Тут р, k є Z).

 

Для  прикладу  розглянемо доведення такого твердження.

При всіх натуральних п, більших за 4,  правильна нерівність

2^п  > п² .

Доведення

При п = 5 нерівність правильна, бо 32 > 25. Припустимо, що ця нерівність правильна при деякому довільному k ≥ 5, тобто

2^k > k².

Тоді

2^k + 2^k > k² + k² .

Але 2^k + 2^k = 2^k+1 і при k ≥ 5  k² ≥ 2k + 1. Тому

2^k+1 > k² + 2 k + 1,.

2^k+1 > (k + 1)²

Як бачимо, доводжувана нерівність правильна при п = 5, і якщо правильна при п = k, то правильна і при п = k + 1. Отже, ця нерівність правильна при всіх натуральних п > 5.

У математиці відомі й інші схеми міркувань методом математичної індукції, але в школі їх не розглядають.

Метод математичної індукції вперше почали застосовувати в XVI-XVIIст. Мавроліко, Паскаль, Бернуллі та інші математики. Широко відомим він став тільки в XIX ст.

Іноді метод математичної індукції називають ще методом досконалої індукції, методом повної математичної індукції, методом переходу від п до п+1 і т. д. Щоб не вносити плутанини, вводити ці терміни в школі не слід.

 

4.               На основі означення.

Розглядається різниця лівої та правої частин нерівності та порівнюється з нулем. Деякі такі доведення були проілюстровані в прикладах раніше.

 

5.               Метод використання очевидних нерівностей.

Покажемо використання цього методу на прикладі.

Приклад

Доведіть нерівність

а² + b² + с² ≥ а b + b с + а с.

Доведення

Очевидно, що при будь-яких значеннях а, b, с виконується така нерівність:

(а - b) + (b - с) + (с - а) ≥ 0.

Звідси:

а² - 2аb + b² + b² - 2bс + с² + с² - 2ас + а² ≥ 0;

2 а² + 2 b² + 2 с² ≥ 2 а b + 2 b с + 2 а с ;

а² + b² + с² ≥ а b + b с + а с.

 

6.               Метод застосування раніше доведеної нерівності.

Розглянемо на прикладі, як можна використовувати нерівність Коші при доведенні інших нерівностей.

 

Приклад

Доведіть, що для додатних чисел а і b справедлива нерівність

.

Доведення

Застосуємо нерівність Коші для додатних чисел а і .

Маємо

.

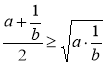Звідси

а + ≥ 2.

Аналогічно доводимо, що b + ≥ 2.

Застосувавши теорему про почленне множення нерівностей, отримаємо:

.

Звідси .

 

7.               Метод геометричної інтерпретації

 

Приклад

Доведіть нерівність:

.

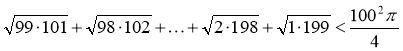Доведення

Розглянемо чверть кола з цен­тром О радіуса 1. Впишемо в неї ступінчасту фігуру, яка склада­ється з 99 прямокутників, так, як показано на рисунку,

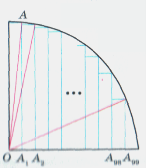ОА₁ = А₁А₂ = … = А₉₈А₉₉ = .

Площа першого прямокутника

S₁ = OA₁·AA₁ = OA₁·.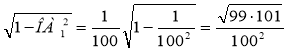

Для другого прямокутника маємо:

S₂ = 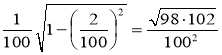і т.д.

S₉₉ = .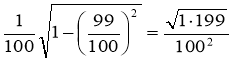

Площа ступінчатої фігури менша від площі чверті круга, тобто

.

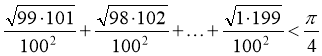Звідси випливає нерівність, що доводиться.

 

Можна розглянути ще й інші нерівності (вчитель надається можливість самостійно визначати які нерівності та коли їх розв’язувати, чи на гуртку, чи на уроці, чи в якийсь інший час). Розглянемо деякі такі задачі.

 

Задача 1.

Довести нерівність

а⁴ + b⁴ ≥ ,якщо а ≥ 0, b ≥ 0, а+ b =1.

Доведення

a²+b² =(a+b)² -2ab = 1-2ab,

а⁴ + b⁴ = (а² + b²)² - 2а² b² = (1 - 2а b)² - 2 а²b².

Отже,

a⁴+b⁴ = (1 - 2а b)² - 2 а²b²  (1)

З умови випливає, що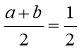

За нерівністю Коші .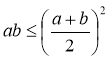

Тому аb ≤ .

Якщо в нерівності (1) замінимо ab більшим значенням , то отримаємо:

а⁴ + b⁴ ≥ = .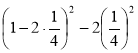

Задача 2.

Довести нерівність

а⁵ + b⁵ ≥ , якщо а ≥ 0, b ≥ 0, а+ b =1.

Доведення

Оскільки

(а + b)⁵ = а⁵ + 5 а⁴ b + 10 а³ b² + 10 а² b³ + 5 а b⁴ + b⁵

і

а + b = 1,

то

а⁵ + b⁵ = 1 -  5ab (a³ + 2a²b + 2ab² + b³)=1 - 5ab ((a + b)(a² - ab+b²)  = 1 - 5ab (a² - ab + b²+ 2ab) =  1 - 5ab ((a+b)² - ab) = 1 - 5ab(1 - ab).

За нерівністю Коші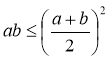  

З умови випливає, що   аb ≤  

Замінимо ab більшим числом , отримаємо:

а⁵ + b⁵ ≥1-5··(1-) = .

Задача 3.

Довести нерівність

а² + b² + с² ≤ 2(а b + b с + а с),

якщо а, b, с - сторони трикутника.

Доведення

Нехай а ≥ b ≤ с, а – b ≤ с , а – с ≤ b , b – с ≤ а. Тоді

(а - b)²  ≤ с²,

(а - с )² ≤ b²,

(b - c)² ≤ a².

Додавши почленно ліві і праві частини нерівнос­тей, отримаємо:

2a² + 2b² + 2c² - 2(ab + ac + bc) ≤ a² + b²+с²,

 a² +b² +c²  ≤ 2(ab + ac + bc).

Задача 4.

Довести нерівність

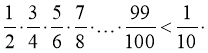
Доведення

Очевидно, що

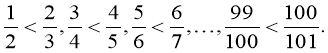
Введемо позначення: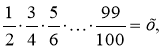

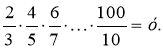
Тоді

х < у , х² < х у ,

х² < , х < < , х < .

Зауваження. Дану нерівність можна узагальнити:

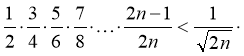
Задача 5.

Довести нерівність

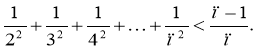
Доведення

Очевидно, що

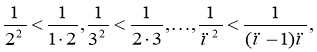
Оскільки

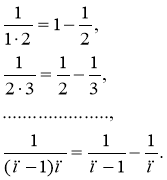
То

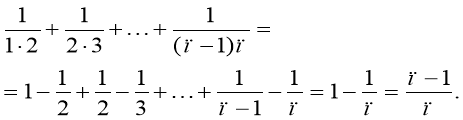
Отже,

 

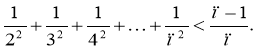
Задача 6.

Довести нерівність

6⁹⁰ > 5⁹⁴.

Доведення

Достатньо довести, що 6⁴⁵ > 5⁴⁷. Оскільки

5⁴⁷ = 5⁴⁵·5²,

 то має виконуватися нерівність

6⁴⁵ > 5⁴⁵·5²,

.

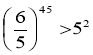Оскільки 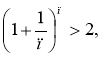де п > 1 і п є N, то

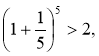і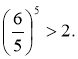

Тому

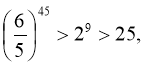25 = 5².

 

Задача 7.

Довести нерівність

де h > -1, п є N (нерівність Бернуллі).

Доведення

1. Перевіримо правильність нерівності, якщо п = 1:

1 + h = 1 + h .

2. Нехай нерівність правильна, якщо п = k:

(1 + h) ^k ≥ 1 + k h.

Доведемо, що вона правильна і тоді, коли п = k + 1, тобто

(1 + h) ^{k +1} ≥ 1 + (k + 1) h .

Маємо:

(1 + h) ^{k +1} = (1 + h)^k(1 + h) ≥ (1 + kh)(1 + h) = 1 + (k + 1) h + k h² ≥

≥ 1 + (k + 1) h.

Отже,

3. За принципом математичної індукції нерівність правильна для п є N.

Ця нерівність є окремим випадком нерівності:

Якщо х₁, х₂, …, х_п мають однаковий знак і х_k > -1, 1 ≤ k ≤ п.

Список використаної літератури.

 

1. Бевз Г.П. Алгебра: підруч. для 9 кл. загальноосвіт. навч. закл. /  Г.П. Бевз, В.Г. Бевз. – К.:Зодіак-ЕКО, 2009. – 288с.
2. Мерзляк А.Г., Полянський В.Б., Якір М.С. Алгебра: підруч. для 9 кл. загальноосвіт. навч. закл. – Х.:Гімназія,2009. – 320с.
3. Мерзляк А.Г., Полянський В.Б., Якір М.С. Алгебра: підруч. для 8 кл. з поглибл. вивченням математики. – Х.:Гімназія,2009. – 386с.
4. Мерзляк А.Г., Полянський В.Б., Якір М.С. Алгебра: підруч. для 9 кл. з поглибл. вивченням математики. – Х.:Гімназія,2009. – 394с.
5. Програма з математики для 5-12 кл. загальноосвітніх навчальних заклазів.- К, 2008.
6. Програма з математики для 8-9 кл. для загальноосвітніх навчальних закладів (класів) з поглибленим вивчення математики.- К, 2008.
7. Бевз Г.П. Методика викладання математики: Навч. посібник. – 3-тє вид., перероб. і  допов. – К.: Вища шк., 1989.  – 367с.
8. Слєпкань З.І. методика навчання математики: Підручник. – 2-ге вил., перероб. і  допов. – К.: Вища шк., 2006. – 582с.
9. Копцюх М.Г., Савич Е.Ф. Доказательство неравенств. – К.: Рад. Школа, 1982. – 160с.
10. Гусев В.А., Мордкович А.Г. Математика: Справ. материалы: Кн. для учащихся. – 2-е узд. – М.: Поросвещение, 1990. – 416с.
11. Груденов Я.Ию Психолого-дидактические основы методики обучения математики. – М.: Педагогіка, 1987.
12. Коваленко В.Г., Гельфанд І.Ф., Ушаков Р.П. доведення нерівностей. – К.: Вища шк., 1979.
13. Козира В. Систематизація та узагальнення знань і вмінь учнів, пов’язаних з доведенням нерівностей // Математика в школі. – №2 – 3. – 1995.
14. Коровин П.П. Неравенства. – М.: Наука, 1983. – 56с.
15. Орач Б. Методи доведення нерівностей // Математика. - №19(319). – Травень 2005. – сс.11-15