Формування професійної компетентності майбутніх фахівців технічних спеціальностей у процесі вивчення математики.

 

 

 

 

 

ЗМІСТ.

Вступ………………………………………………………………………. 2

1. Актуальність теми…………………………………………………. 4
2. Історична довідка………………………………………………….. 7
3. Етапи побудови математичних моделей…………………………. 8
4. Переваги і недоліки математичного моделювання……………… 9
5. Формування загальних та професійних компетенцій на заняттях математики………………………………………………………… 9
6. Формування професійної компетентності майбутніх фахівців технічних спеціальностей у процесі вивчення математики у Роменському коледжі КНЕУ…….……………………………….. 11

Висновки………………………………………………………………….. 31

Список використаної літератури………………………………………..  33

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ.

Протягом багатьох сторіч математика є невід’ємним елементом системи освіти в усьому світі. Пояснюється це унікальною здатністю навчального предмета «математика» у формуванні особистості. Освітній, виховний і розвиваючий потенціал математики величезний.

Усвідомлюючи роль математичних дисциплін в професійній підготовці майбутніх фахівців, слід зазначити зниження рівня природничо-наукової і математичної підготовки у сучасної молоді, що приходить до вищого навчального закладу. 

На сучасному етапі розвитку суспільства у фокусі освіти виявилася методологічна підготовка студента по кожній дисципліні і насамперед – по фундаментальних. Особливе значення починають здобувати не тільки міцність і глибина, але й затребуваність фундаменту, на якім вибудовується професійна підготовка. Вирішуючи питання вдосконалювання професійної освіти і такої його важливої складової як математична освіта майбутніх фахівців необхідно виходити з об’єктивно існуючого факту надзвичайної динамічності системи «наука – освіта – виробництво». Майбутні фахівці повинні мати вміння і професійну мобільність – оперативно реагувати на постійно виникаючі зміни в практичній і науковій діяльності, суспільної практики в цілому. Це стане можливо, якщо вищій навчальний заклад озброїть випускника загальною інтегральною (тобто міждисциплінарною) методологією професійної діяльності.

Підвищення якості підготовки фахівців, покликаних розв’язувати задачі, пов’язані з функціонуванням окремих сфер життя суспільства, вимагає в сучасних умовах від студентів не тільки оволодіння певним змістом освіти, але й розвитку в них таких особистісних якостей і рис характеру, як сила волі, відповідальність за свої вчинки, здатність відстоювати свої погляди і переконання. Наукові знання – це ще не все, що необхідно сучасній людині, щоб успішно соціалізуватися. На зміну парадигми знання освіти приходить культурологічний особистісно-орієнтований підхід, націлений на розвиток творчої складової кожної людини.

Математична освіченість – це підсистема загальної освіченості студентів. Вивчення дисциплін математичного циклу сприяє не тільки накопиченню певної системи знань, умінь і навичок, але й розвитку інтелектуальної сфери студентів, формуванню різних способів мислення. Зараз математичну освіту слід розглядати як найважливішу складову в системі фундаментальної підготовки сучасного економіста. Метою такої підготовки стає готовність студента до неперервної самоосвіти і практичного застосування математичних знань.

У процесі вивчення математики студенти опановують такі прийоми і методи мислення, як індукція і дедукція, аналіз і синтез, узагальнення і конкретизація, класифікація і систематизація. Уміння формулювати, обґрунтовувати і доводити твердження розвиває логічне мислення. Засобами математики розвиваються вольові якості особистості, наполегливість і цілеспрямованість, пізнавальна активність і самостійність, дисциплінованість.

Виховання наукового світогляду є однією з основних задач вищої школи, і в розв’язання цієї задачі кожен предмет вносить свій особливий і неповторний внесок. Математичні дисципліни мають величезні можливості для наявного представлення могутності, загальності і універсальності наукових методів у пізнанні навколишнього світу, для виявлення значення абстрактного мислення в наукових і практичних питаннях. 

Зближення викладання математичних дисциплін з потребами інших дисциплін розкриває широкі можливості для демонстрації місця математики та її понять у пізнанні людиною природи і суспільних явищ.

Згідно з вимогами активізації навчального процесу у вищій школі ставиться задача ввести в зміст навчання формування навичок творчої діяльності, розробку системи проблемних задач по навчальних предметах, розв’язок яких студентами буде сприяти розвитку в них творчого мислення, пізнавальної самостійності. Основними рисами творчої діяльності, які слід прагнути прищеплювати студентам у процесі викладання математики у вузі, є: самостійне перенесення знань і навичок у нову ситуацію; бачення нової проблеми в знайомій ситуації; бачення нової функції об’єкта; знаходження різних способів вирішення проблеми. 

Найважливішим показником результативності навчального процесу повинен бути інтенсивний розумовий розвиток студентів, їх неперервне проникнення в сутність досліджуваних предметів, процесів і явищ, зростання пізнавальних інтересів, прагнення до поглиблення своїх знань і до формування діалектичного мислення.

Однією із провідних характеристик людини з високою культурою є здатність до безперервної самоосвіти, самовиховання, саморозвитку. Вивчення дисциплін математичного циклу сприяє розвитку здатності студентів до інтелектуальної і творчої діяльності, до сприйняття і переробки нової інформації, впливає на розвиток особистісних і професійно значимих якостей майбутніх фахівців, що дозволяють їм самореалізуватися в сфері майбутньої професійної діяльності. Це відноситься до всього циклу математичних дисциплін (вища математика, теорія ймовірностей і математична статистика, економічне моделювання, математичні методи в економіці, дослідження операцій і математичне програмування). Кожна із цих дисциплін крім загальних цілей має і конкретні цілі навчання, що накладає відбиток на способи реалізації професійної спрямованості та рівень міжпредметних зв’язків у кожній навчальній дисципліні.

Таким чином, математичні дисципліни займають дуже істотне місце в системі професійної підготовки майбутніх фахівців, на сучасному рівні навчають, виховують, розвивають молодь, і є могутнім засобом підвищення загального рівня освіченості особистості в цілому.
 

Актуальність теми.

Одним із основних завдань сучасної освіти є формування практично компетентної, творчої особистості. Тому пошук нових можливостей підсилення прикладної спрямованості курсу математики, засобів формування навичок математичного моделювання є перспективним напрямком досліджень у сфері теорії і методики навчання математики.

Згідно навчальних програм з математики за новим Державним стандартом в основу побудови змісту й організації процесу навчання математики покладено компетентісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності як здатності студента успішно діяти в навчальних і життєвих ситуаціях і нести відповідальність за свої дії. Компетентність є особистісним утворенням, яке формується на основі здобутих знань, досвіду діяльності, вироблених ціннісних орієнтацій, ставлень, оцінок.

Навчання математики передбачає передусім формування предметної математичної компетентності, сутнісний опис якої подано у розділі «Державні вимоги до загальноосвітньої підготовки учнів» цієї програми. Крім того, воно має зробити певний внесок у формування певних ключових (більш загальних, що виходять за межі одного предмета) компетентностей, зокрема загальнонавчальної (уміння вчитися), комунікативної (здатності грамотно формулювати і висловлювати судження), загальнокультурної та інших. Формування зазначених компетентностей підпорядковується реалізації загальних завдань математичної освіти, що здійснюється на всіх етапах навчання. До них  належать:

• Формування ставлення до математики як невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві на основі ознайомлення з ідеями і методами математики як універсальної мови науки і техніки, ефективного засобу моделювання і дослідження процесів і явищ навколишнього світу;
• Забезпечення оволодіння студентами математичною мовою, розуміння ними математичної символіки, математичних формул і моделей як таких, що дають змогу описувати загальні властивості обєктів, процесів та явищ;
• Формування здатності логічно обгрунтовувати та доводити математичні твердження, застосовувати математичні методи у процесі розв’язування навчальних і практичних задач, використовувати математичні знання і вміння під час вивчення інших навчальних предметів;
• Розвиток умінь працювати з підручником, опрацьовувати математичні тексти, шукати і використовувати додаткову навчальну інформацію, критично оцінювати здобуту інформацію та її джерела, виокремлювати головне, аналізувати, робити висновки, використовувати отриману інформацію в особистому інформацію в особистому житті;
• Формування здатності оцінювати правильність і раціональність розв’язування математичних задач, обгрунтовувати твердження, приймати рішення в умовах неповної, надлишкової, точної та ймовірнісної інформації.

Необхідною умовою формування компетентностей є діяльнісна спрямованість навчання, яка передбачає постійне включення студентів до різних видів педагогічно доцільної активної навчально-пізнавальної діяльності, а також практична його спрямованість. Необхідно, де це можливо, не лише показувати виникнення математичного факту із практичної ситуації, а й ілюструвати його застосування на практиці.

Тому, зараз завдання викладача – керувати  пізнавальною діяльністю студента та допомагати йому отримати той рівень навчальних досягнень, який він може одержати в міру своїх здібностей і можливостей, хоче одержати для подальшого свого розвитку в умовах життєтворчості та майбутнього життєвого шляху.

Важливо переконати студентів у необхідності вивчення математики, адже вона дисциплінує розум, привчає до логічного мислення. Можливо, формули, доведення тотожностей і теорем не запам’ятаються на все життя, але залишиться звичка міркувати, збережеться вміння пояснювати, доводити не тільки другим , а й самому собі якісь істини, закріпиться вміння шукати і знаходити раціональні шляхи розв’язання життєвих проблем.

Сильне враження на студентів справляє обгрунтування необхідності вивчення математики у зв’язку з потребами вивчення спецдисциплін.

У концепції математичної освіти підкреслюється, що остання повинна спиратись на розвивальний характер навчання і прикладну спрямованість, розвиток вміння застосовувати знання до розв’язування практичних задач, які виникають за межами математики і розв’язуються математичними методами. У евристичному навчанні математики розвязуються прикладних задач набуває особистісного значення.

На думку О.І. Скафи, яка визначає евристичне навчання математики як реалізацію теоретико-методичних основ формування прийомів навчально-пізнавальної евристичної діяльності в умовах інформаційно-комунікаційних технологій, розглядаються евристичні прийоми, як особливі прийоми, які сформувалися в ході розвязування одних задач і більш-менш свідомо переносяться на інші.

Навчання загальним та спеціальним евристичним прийомам формує евристичну діяльність і більш ефективно сприяє розвитку творчого мислення. Процес формування евристичної діяльності та творчість взаємопов’язані між собою компоненти. Як відзначає А.В.Хуторський, евристика – наука про відкриття нового, а творчість – процес створення нового, тобто без сформованих у студента евристичних прийомів діяльності неможливо організувати і керувати процесом формування творчої діяльності.

У реальному навчальному процесі прикладна і практична спрямованість задач функціонують, як правило, спільно. Проте, перше поняття більш загальне, воно визначає мету вивчення математики, а друге – засоби, форми і методи роботи.

Проблемі реалізації прикладної спрямованості навчання математики присвячені дослідження Г.П. Бевза, Л.М. Вивальнюка, Ю.В. Горошка, А.М. Гнеденка, О.С. Дубінчук, М.І. Жалдака, В.М. Лейфури, З.І. Слєпкань, О.І. Скафи, Л.О. Соколенко, Л.М. Фрідмана, І.М. Шапіро, В.О. Швеця, М.І. Шкіля та ін.

Аналіз наукових досліджень фундаторів математичного моделювання та практичного стану проблеми свідчить про те, що це поняття слід розглядати як один з параметрів, за яким можна було б оцінити внесок математики в розвиток особистості студента.

Для того, щоб студенти оволоділи ідеями і методами сучасної математики, необхідно  ввести їх у зміст навчання у явному вигляді, оскільки актуально усвідомлюється лише той зміст навчального матеріалу, який є предметом цілеспрямованої активності суб’єкта.

Актуальною залишається проблема відбору змісту особистісно-орієнтованої математичної освіти та питання формування понять математична модель та математичне моделювання в процесі евристичного навчання.

Під час побудови математичної моделі прикладної задачі звичайно виникає потреба побудови математичних моделей реальних об’єктів, про які йдеться в задачі. Математичні моделі реального процесу або об’єкта можуть бути подані у вигляді формули,  математичного малюнка,  математичного твердження, геометричної фігури, пропорції тощо. У реальному житті є багато задач, які, на перший погляд, не мають між собою нічого спільного. Але часто для їх розв’язання можна використовувати одну й ту саму математичну модель. Отже, вміння працювати з однією математичною моделлю дає можливість розв’язувати різні прикладні задачі. Навчання студентів самостійно здійснювати дослідження, використовувати нестандартні підходи до розв’язування задач сприяє результативному та ефективному процесу формування творчого мислення студента, підвищення навчально-пізнавальної діяльності.  

 

Історична довідка

Мабуть, немає сьогодні такої галузі знань, де б не застосовувалися досягнення математики. Академік Д.О. Граве говорив: «Ключ до розв’язання багатьох наукових задач – їхній вдалий переклад мовою математики». Справді, формулювання задач з різних галузей знань містять нематематичні поняття. Якщо математик бере участь у розв’язуванні такої задачі, то він насамперед прагне перекласти її математичною мовою. Результат такого перекладу називають математичною моделлю.

Модель — це деякий матеріал чи описово представлений об'єкт або явище, що є спрощеною версією модельованого об'єкта або явища (прототипу) і в достатній мірі повторює властивості, суттєві для цілей конкретного моделювання (опускаючи несуттєві властивості, у яких він може відрізнятися від прототипу). Розрізняють натурні, фізичні, теоретичні, математичні та ін. моделі.

Моделювання  — це метод дослідження явищ і процесів, що ґрунтується на заміні конкретного об'єкта досліджень (оригіналу) іншим, подібним до нього (моделлю) .

Математи́чне моделюва́ння — метод дослідження процесів або явищ шляхом створення їхніх математичних моделей і дослідження цих моделей. Сутність його полягає в тому, що взаємозв'язок досліджуваних явищ і факторів передається у формі конкретних математичних символів, рівнянь.

Математичне моделювання дозволяє замінити реальний об’єкт його моделлю і потім вивчати останню . Як і у випадку будь – якого моделювання, математична модель не описує явище абсолютно адекватно, що залишає актуальним питання про застосування отриманих таким шляхом даних.

Математичне моделювання тією чи іншою мірою застосовують усі природничі і суспільні науки , що використовують математичний апарат для одержання спрощеного опису реальності за допомогою математичних понять.

Математичні моделі досліджуються, як правило, допомогою аналогових обчислювальних машин, цифрових обчислювальних машин, комп’ютерів. На початку 60-их років було розроблено один із методів математичного моделювання – квазіаналогове моделювання. Цей метод полягає в дослідженні явища або процесу іншої фізичної природи, яке описується співвідношеннями, еквівалентними до результатів щодо того процесу , який вивчаэться.

 

Етапи побудови математичних моделей

У побудові математичних моделей складних процесів виділяються наступні етапи. 
І етап моделювання. Визначають мету і задачі моделювання. На цьому етапі повинні бути сформульовані гіпотеза і питання, відповідь на які повинна дати модель.

ІІ етап моделювання. Збір нової або ревізія існуючої інформації про об'єкт, аналіз і обробка даних. Ті реальні явища , які моделюються, повинні бути ретельно вивчені: виявлені головні компоненти і встановлені закони, що визначають характер взаємодії між ними. Якщо неясно, як пов'язані між собою реальні об'єкти, побудова адекватної моделі неможлива.

ІІІ етап моделювання . За допомогою формул, рівнянь, нерівностей, виразів тощо, створюють математичну теорію, що описує процеси, які вивчаються, тобто будують модель.

ІV етап моделювання . У відповідності з метою дослідження розв’язують прикладні задачі за допомогою математичних виразів, формул, рівнянь, нерівностей, функцій, графіків тощо.
V етап моделювання . Проводять аналіз, роблять висновки, перевіряють модель, звіряють результати з дійсністю, оцінюють адекватність вибраної моделі. При значному розходженні відомостей модель відкидають або вдосконалюють . При узгодженості результатів моделі використовують для прогнозу за допомогою введення в них різних параметрів.

 Але сама по собі математична модель не може служити абсолютним доказом правильності тієї чи іншої гіпотези , тому що може виявитися , що різні гіпотези призводять до схожих результатів , але вона служить одним із шляхів аналізу реальності.

 

Переваги і недоліки математичного моделювання

Метод математичного моделювання у разі правильно побудованої моделі допомагає побачити те, що важко або неможливо перевірити в експерименті, дозволяє відтворювати такі процеси , спостереження яких в природі вимагало б багато сил і часу. У математичних моделях можна «програвати» різні варіанти - встановлювати різні зв'язки, комбінувати окремі фактори, спрощувати або ускладнювати структуру системи,  змінювати послідовність і силу впливу на неї. Все це дає можливість краще зрозуміти механізми, що діють в природних умовах.

Моделюють різні за характером процеси, що відбуваються в реальному середовищі, як, наприклад, окремі типи екологічних взаємодій хижак - жертва, паразит - господар, конкурентні відносини, мутуалізм та ін. Математичними моделями описуються і перевіряються різні варіанти динаміки чисельності популяцій, продукційні процеси в екосистемах, процес відновлення систем при різних формах порушень та багато інших явищ.

Недоліки математичних моделей полягають часто в складності математичного апарату. Виникають труднощі перекладу результатів з мови математики на мову реального життя. Мабуть, найбільший недолік математичної моделі пов'язаний з тим спотворенням, яке можна привнести до самої проблеми, наполегливо відстоюючи конкретну модель, навіть якщо насправді вона не відповідає фактам, а також з тими труднощами, які виникають іноді при необхідності відмовитися від моделі, що опинилася неперспективною.

 

Формування загальних та професійних компетенцій на заняттях математики.

Молодій людині, що вступає в самостійне життя в умовах сучасного ринку праці та інформаційного простору, що швидко змінюється, необхідно бути ефективним, конкурентоспроможним працівником. Вона повинна бути творчою,самостійною, відповідальною, комунікабельною людиною, що здатна вирішувати проблеми особисті і колективу. Їй повинна бути властива потреба до пізнання нового, вміння знаходити та відбирати необхідну інформацію. Всі ці якості можна успішно формувати, використовуючи компетентісний підхід у навчанні математики, що є одним одним із особистісних та соціальних змістів освіти.

 

А.В. Хуторський, розрізняючи поняття «компетенція» та «компетентність», пропонує наступні визначення.

Компетенція – включає сукупність взаємопов’язаних якостей особистості (знань, умінь, навичок, способів діяльності), що задані відносно визначеного кола предметів та процесів, та необхідних для якісної продуктивної діяльності відносно них.

Компетентність – володіння людиною відповідною компетенцією, що включає її особистісне відношення до неї та предмету діяльності.

Випускник, що засвоїв програму, повинен володіти загальними компетенція ми, що включають в себе здатність:

1.                   Розуміти суть та соціальну значимість своєї майбутньої професії, проявляти до неї стійкий інтерес.
2.                   Організовувати власну діяльність, виходячи з мети та способів її досягнення, визначених керівником.
3.                   Аналізувати виробничу ситуацію, здійснювати поточний та підсумковий контроль, оцінку та корекцію власної діяльності, нести відповідальність за результати своєї роботи.
4.                   Здійснювати пошук інформації, необхідний для ефективного виконання професійних задач.
5.                   Використовувати інформаційно-комунікаційні технології у професійній діяльності.
6.                   Працювати в колективі та команді, ефективно спілкуватися з колегами, керівництвом, клієнтами.
7.                   Виконувати військовий обов’язок, у тому числі із застосуванням професійних знань (для юнаків).

Всіма цими компетенція ми повинен володіти випускник при вивченні дисциплін природничо-математичного циклу. Крім того, він повинен володіти професійними компетенціями, що відповідають основним видам професійної діяльності.

 

 

Формування професійної компетентності майбутніх фахівців технічних спеціальностей у процесі вивчення математики у Роменському коледжі КНЕУ.

Однією з задач викладання математики є розвиток зацікавленості дисципліною, що досягається запровадженням у навчальний процес викладачами коледжу інноваційних технологій викладання, активних та інтерактивних методів навчання, використанням електронних освітніх ресурсів, що напрямлені на підготовку майбутнього кваліфікованого спеціаліста. Викладачі використовують на заняттях ігрові форми навчання, застосовуючи такі технології, як робота в групах, проблемне навчання, пошуковий та диференційований методи навчання математики.

Процес формування загальних та професійних компетенцій студентів нашого коледжу відбувається вже на першому курсі, а їх розвиток – на другому та третьому курсах навчання.

В Роменському коледжі КНЕУ щорічно проходить «Тиждень природничо-математичних дисциплін», під час якого проводяться цікаві відкриті заходи, конкурси, олімпіади. Викладачі циклової комісії природничо-математичних дисциплін до організації та проведення тижня завжди підходять творчо, шукають нові форми і методи проведення заходів, залучаючи все більшу кількість студентів. Тому і цього року він пройшов насичено та цікаво як для студентів так і для самих викладачів, панувала атмосфера взаємної підтримки і поваги. Усі учасники отримали позитивні емоції і ще протягом тривалого часу продовжували згадувати труднощі підготовки та втіху від результатів виступів та досягнень.

Зокрема, з математики цього року проведено І тур Всеукраїнської студентської олімпіади з математики, розважально-інтелектуальна гра з математики «Еврика» та конкурс відео презентацій на тему: «Застосування математичного моделювання у моїй професії та повсякденному житті», де кожен активний студент намагався якомога краще донести результати своєї клопіткої підготовки до аудиторії.

Проведення тижня циклової комісії природничо-математичних дисциплін сприяє підвищенню професійної майстерності, професійної орієнтації, прояву творчих здібностей студентів. Викладачі постійно прагнуть готувати кваліфікованих фахівців відповідного рівня і профілю, конкурентоспроможних на ринку праці.

Результатом  тижня циклової комісії  стали подарунки, дипломи, нагороди, подяки.

Тиждень циклової комісії природничо-математичних дисциплін - це завжди хвилююча і феєрична подія, адже першокурсники направляють всі зусилля студентського запалу, енергії, завзяття на створення незабутньої атмосфери, інтриги, що виходить за межі стандартів під час підготовки виховних заходів.

І тур Всеукраїнської олімпіади з математики.

Розважально-інтелектуальна гра з математики «Еврика»

 

 

Конкурс відео презентацій на тему: «Застосування математичного моделювання у моїй професії та повсякденному житті»

 

 

На своїх заняттях також використовую компетентісний підхід, намагаюсь наповнити математичну освіту знаннями, уміннями і навичками, пов’язаними з особистим досвідом та потребами студента з тим, щоб він міг здійснювати продуктивну та осмислену діяльність по відношенню до об’єктів реальної діяльності.

 

На заняттях математики:

1. Навчаю ставити мету та планувати діяльність по її досягненню.

Приклад 1: урок засвоєння нових знань з теми «Циліндр»

На столі викладаю моделі тіл обертання (куля, циліндр, конус) і многогранників (призми, піраміди). Студентам  пропоную розділити дані фігури на дві групи за принципом: в першу групу помістити вивчені фігури, а в другу невивчені. Потім прошу дати назву даними групам фігур (другу групу спробувати назвати на інтуїтивному рівні). Якщо вони не зможуть дати назву другої групи, то оголошую її сама. Далі пропоную розглянути слайди із зображенням різних предметів в яких є циліндр і знайти в них спільне. Після того, як студенти впораються із завданням, прошу визначити тему і мету заняття, задаючи навідні запитання.

Приклад 2: при вирішенні задач, рівнянь, побудові графіків функцій, і т.д. прошу студентів скласти план розв’язання.

На  занятті на тему: «Способи розв’язування тригонометричних рівнянь» (що зводяться до квадратних)

      Після проведення етапу актуалізації знань, на якому студенти розв’язують квадратні рівняння, ставлю проблему: як вирішити дане тригонометричне рівняння. Таким чином, студенти вибудовують алгоритм розв’язання  таких рівнянь.

2. Вчу добувати потрібну інформацію, використовуючи доступні джерела (довідники, підручники, словники, ЗМІ, ресурси Internet) і передавати її.

Приклад 3: при повторенні теми: «Теорема Піфагора» на 1 курсі даю завдання відшукати і представити у вигляді доповіді різні способи доведення  цієї теореми.

Студенти протягом навчального року готують презентації, реферати, проекти, доповіді, повідомлення на різні математичні теми.

3. Вдосконалюю навички роботи в команді, вчу висловлювати і аргументовано відстоювати свою думку

Приклад 4: урок по темі: «Піраміда»

Робота в міні – групах

Розбиваю групу на 4 міні-групи. Кожній групі видається ватман в центрі якого написано слово піраміда. Зліва в стовпчик записані слова відносяться до цього головного слову (грань, ребро, правильна, висота, вершина, і т.д.). Необхідно скласти карту поняття піраміда. (Встановити взаємозв'язки між поняттями) і аргументовано обгрунтувати свою роботу.

Робота в парах:

При відпрацюванні визначення піраміди, які навчаються працюючи з підручником, читають визначення «про себе», потім вголос, потім сусідові по парті

Студетам пропонується подивитися слайд, на якому поступово з'являються елементи піраміди і скласти план її побудови, працюючи в парах. За бажанням пара представляє свій варіант плану.

4. Вчу вносити посильний внесок у досягнення загального результату

 На узагальнюючих уроках, розбиваю студентів на групи, яким видається комплект завдань.

Та група, яка швидше вирішить всі завдання виграє. Кожен учасник групи повинен відзвітувати про виконану ним роботу. Роботу кожного учасника оцінює вся група.

При проведенні тижнів математики прагну складати завдання, турніри, конкурси, вікторини, олімпіади так щоб кожен студент в групі міг взяти участь. Стимулюю призовими місцями, призами, грамотами.

5. Навчаю брати на себе відповідальність за керівництво міні - групою

При роботі в групах завжди вибирається керівник групи. Намагаюся, щоб студенти обирали самі керівника (щоразу це нова людина).

6. Прищеплюю навички самостійної, творчої роботи

Практично на кожному занятті студенти виконують самостійну роботу, використовуючи індивідуальні картки. Це можуть бути і тести, і практичні роботи.

Студенти протягом навчального року готують презентації, реферати, проекти, доповіді, повідомлення на різні математичні теми, розробляють плакати до занять.

7. Вчу грамотно використовувати в мові математичні терміни

Особливо приділяю цьому увагу. Стежу за грамотністю математичної мови як письмовою, так і усною. Проводжу словникові математичні диктанти.

8. Прищеплюю навички самоконтролю і взаємоконтролю

Наприкінці заняття відстежую рефлексію і самооцінку.

Приклад 5: Заняття за темою «Конус»

Наприкінці заняття кожному студенту видаються лист з нижченаведеними питаннями

Поставте «+» або «-» навпроти кожного твердження:

Я знаю визначення конуса

Я знаю елементи конуса

Я зможу відрізнити конус від інших геометричних просторових фігур

Я зможу пояснити відсутньому на занятті студенту, як побудувати конус і що це таке

Я знаю, які тіла називаються тілами обертання

Я знаю, чому конус відноситься до тіл обертання

Я знаю, де застосовується конус в повсякденному житті

Я знаю два способи утворення конуса

Продовжіть речення:

Мій настрій на уроці ...

Мені сподобалося ...

Мені не сподобалося ....

Оцініть свою діяльність на уроці за п'ятибальною шкалою

Працюючи в міні групах,студенти оцінюють свою роботу і роботу товаришів. Так як цьому приділяється увага протягом навчального року, то вони звикають висловлювати свою думку і адекватно оцінювати себе та інших.

При проведенні тестів я використовую на заняттях взаємоконтроль в парах. Після написання тесту пара обмінюється роботами. Студент самостійно перевіряє роботу товариша і виставляє оцінку. При усній відповіді прошу студента проаналізувати свою відповідь і поставити собі оцінку. А решта вносять свої коментарі і або корегують оцінку, або погоджуються з нею.

9. Вчу застосовувати математичне моделювання  в реальних ситуаціях

Приклад 6: заняття по темі «Призма»

Пропоную вирішити завдання: необхідно на дачі встановити резервуар для води ємністю в 10 м3 на площі розміром 2,5 м × 1,75 м, що служить для нього дном. Висота резервуара невідома.

10. На заняттях математики я частково сприяю формуванню професійних компетенцій:

пропоную студентам розв’язати  геометричні задачі із професійним нахилом:

Приклад 7:

Для спеціальності «Обслуговування  і  ремонт обладнання  нафтових і газових промислів»   

ЗАДАЧА   №1

     Визначити  коефіцієнт  подачі  і  привідну  потужність  для  приводу  горизонтального  двоциліндрового  з  циліндрами  двохсторонньої  дії  бурового  насосу  при  наступних   даних:

     D -        діаметр  поршня ,  м ;

      d –        діаметр  штока ,  м;

      S –        хід  поршня ,  м;

      n –         число  ходів ,об/хв ;

      _м -        механічний  ККД.

     В  процесі  роботи  насос  розвиває  тиск  P  в  МПа  ,  а  при  дослідженні  місткість  об’ємом  V,  м   закачується  за  час  Т,  сек.

РОЗВ’ЯЗАННЯ

    а) Визначаємо  теоретичну  продуктивність  насосу:

  Q _ф = (2 - d ) ,   м/ сек.

  б) Визначаємо  дійсну  секундну  продуктивність  насосу:

Q_ф = ,  м/сек.

 в) Визначаємо  коефіцієнт  подачі  насосу:

  ₀ = ,    

 г) Визначаємо  приводну  потужність  насосу:

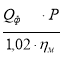  = 1000 ,  кВт.

 

 

ЗАДАЧА   №2

     Визначити  фактичну  продуктивність  трьохциліндрового  бурового  насоса  односторонньої  дії  при  наступних  даних:

     D  -       діаметр  поршня  , мм;

     S  -        хід  поршня  , мм;

     n  -        число  ходів  , об/хв;

  -       коефіцієнт  подачі.

z –       кількість циліндрів насосу

РОЗВ’ЯЗАННЯ

        Фактична  продуктивність  трьохциліндрового  бурового  насоса  односторонньої  дії  визначається  за  формулою :

      Q_ф   =   =   , м³/сек.        

    де   z  =  3 

  Тоді :

    Q_ф  = ,  м³/сек.

Задача  №3

Визначити  фактичну  продуктивність  одноциліндрового  поршневого  насоса

 простої  дії  Q_ф,  якщо: 

довжина  хода  поршня    S  =  300 мм,

діаметр  циліндрової  втулки  D  =  150  мм,

число  подвійних  ходів   n  =  30  об/хв

коефіцієнт  подачі    =  0,85.

РОЗВ’ЯЗАННЯ

Фактична  продуктивність  одноциліндрового  поршневого  насоса  простої

                дії  визначається  за формулою:

 

Q_ф  =      =      (м³/сек)

де  F  -  площа  перерізу  поршня  в  м².

Задача  №4

Визначити  фактичну  продуктивність  горизонтального  двоциліндрового  насоса  подвійної  дії  Q_ф,  якщо: 

довжина  хода  поршня    S  =  450 мм, 

діаметр  циліндрової  втулки  D  =  200  мм, 

діаметр  штока  d  =  60  мм, 

число  подвійних  ходів   n  =  55  об/хв 

 коефіцієнт  подачі    =  0,9.

РОЗВ’ЯЗАННЯ

Фактична  продуктивність  для  даного  насоса  визначається  за формулою:

Q_ф  =      =      (м³/сек)

де  f  -  площа  перерізу  штоку  в  м².

Задача  №5

Визначити  фактичну  продуктивність  горизонтального  трьохциліндрового  насоса  подвійної  дії  Q_ф,  якщо: 

довжина  хода  поршня    S  =  450 мм, 

діаметр  циліндрової  втулки  D  =  200  мм, 

діаметр  штока  d  =  60  мм, 

число  подвійних  ходів   n  =  55  об/хв 

                 коефіцієнт  подачі    =  0,9.

РОЗВ’ЯЗАННЯ

Фактична  продуктивність  трьохциліндрового  насоса   подвійної  дії   визначається  за формулою:

Q_ф  =      =      (м³/сек).

                                                                                

• Для спеціальності «Обслуговування комп’ютерних систем і мереж»:

Задача 1. Розрахувати методом контурних струмів всі струми у колі Рис. П1 при таких заданих параметрах: R1=26(Ом), R2=10(Ом), R3=18(Ом), R4=14(Ом), R5=20(Ом), R6=8(Ом), E2=20(В), E7=24(В), J=2(А). 

У колі чотири незалежних контури. За ме-тодом контурних струмів потрібно скласти три рівняння, оскільки  контурний струм  відомий .  За заданими напрямками контурних струмів записуємо рівняння:

       

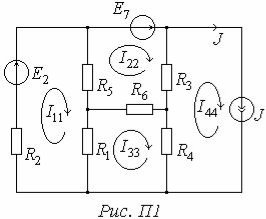
Власні контурні опори: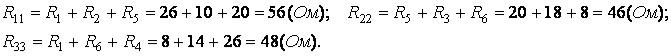 
 

Взаємні контурні опори при однакових напрямках контурних струмів – від’ємні:

 

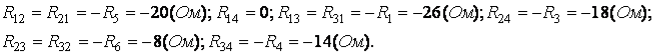
Контурні ЕРС:    Підставляєм ці значення у початкову систему рівнянь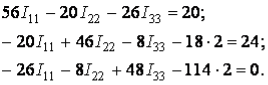
 

Після спрощення:

 

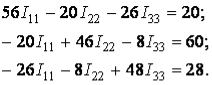
Розв’язуємо систему рівнянь за допомогою визначників:

 

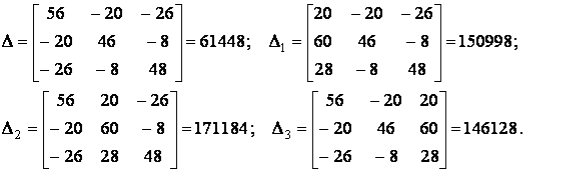
Знаходимо контурні струми:

 

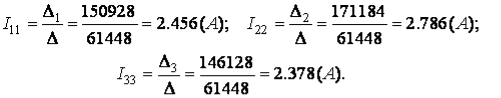
Всі контурні струми додатні - дійсні їх напрямки співпадають із виб-раними. Для перевірки вірності розрахунків потрібно підставити знайдені кон-турні струми у початкові рівняння, при наявності тотожності розв’язок вважа-ється вірним. Допустима похибка не більше 1%.

 

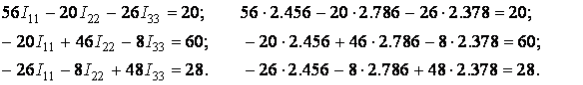
Струми  віток дорівнюють алгебраїчним сумам контурних струмів, що протікають у  вітках.

 

 

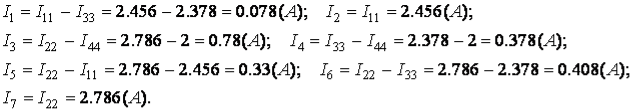
2. До розподільного пристрою приєднано три споживача з номінальною потужністю 20, 15 і 5 кВт. Імовірність включеного стану споживачів дорівнює Р1 = 0,6, Р2 = 0,7; Р3 = 0,5. Визначити ймовірність того, що навантаження на розподільчому пристрої складе 40 кВт.
3. На підприємство надійшли комплектуючі для 10 комп'ютерів. Скількома способами можна розподілити 10 надійшли материнських плат для цих комп'ютерів.
4. В обчислювальному центрі працює 5 персональних комп'ютерів (ПК). Найпростіший потік завдань, що надходять на ВЦ, має інтенсивність 10 завдань на годину. Середній час вирішення завдання дорівнює 12 хв. Заявка отримує відмову, якщо всі ПК зайняті. Знайдіть імовірнісні характеристики системи обслуговування.

При вирішенні перелічених вище завдань у студентів формуються такі професійні компетенції як самостійне розв’язання  відповідної проблеми, знання та вміння застосовувати основні поняття математики, вміння логічно мислити, вміння аналізувати та оцінювати за певними критеріями вивчені явища, процеси, об'єкти, виконавська дисципліна і організованість.

Ще  одним  із прийомів розвитку професійних та інших компетенцій у студентів є проведення семінарських занять, занять захисту проектів.

Семінарські заняття сприяють розвитку самостійності, привчають молодь до вдумливої роботи над літературними джерелами та архівними матеріалами. Вони допомагають розширити світогляд студентів, привчають її до критичного і творчого мислення, до публічних виступів і полеміки з тих чи інших питань.

 

В курсі математики заплановано 4 семінарських заняття:

 

N з/п	Назва теми	Кількість годин
1	Застосування степеневих, показникових та логарифмічних функцій до моделювання процесів	2
2	Застосування тригонометричних функцій до моделювання процесів	2
3	Застосування похідної до моделювання процесів	2
4	Застосування інтеграла до моделювання процесів	2

 

З вищої математики ми проводимо 7 семінарських занять:

 

N з/п	Назва теми	Кількість годин
1	Узагальнення поняття комплексного числа	2
2	Лінії на площині і в просторі	2
3	Похідна функції та її застосування	2
4	Функції багатьох змінних	2
5	Інтеграл та його застосування	2
6	Лінійні диференціальні рівняння	2
7	Числові та функціональні ряди, їх застосування	2

 

 

В основному практикую семінари з груповою роботою:

         Група заздалегідь поділена на підгрупи по два чоловіки в кожній. Підгрупи працюють в парі. Кожна підгрупа отримує завдання, яке визначає, по якому питанню теми вони повинні опитати підгрупу-напарницю, прокоментувати відповідь та оцінити її. Відповідаючі студенти повинні усно дати відповідь та продемонструвати розв’язування задачі. Решта студентів групи, які не приймають участі в цей момент в опитуванні та не розв’язують задачу, можуть доповнити відповідь, або задати запитання, яке відноситься до даної теми і не було задане опитуючими.

 

Як приклад семінару – захисту проекту з використанням групової роботи було проведене відкрите заняття на тему: «Застосування інтеграла до моделювання процесів» в групі К-2-1.

                  За два тижні до проведення заняття група була розбита на чотири команди, кожна з яких одержала завдання створити і презентувати інформаційно-дослідницький проект на тему:  «Застосування інтеграла до моделювання процесів», причому кожна команда отримує одне з вузько направлених завдань:

• «Застосування інтеграла до моделювання процесів у математиці»;
• «Застосування інтеграла до моделювання процесів у фізиці та техніці»;
• «Застосування інтеграла до моделювання процесів в економіці, бізнесі та бухгалтерії»
• «Застосування інтегралу згортки для синтезу цифрових систем» 

 

                   Щоб презентувати свою роботу кожній команді необхідно оформити зібрану інформацію у вигляді презентації «PowerPoint» та буклету «Publisher», в презентації крім теоретичних викладок звернути особливу увагу на приклади застосування інтеграла, підготувати бліц-опитування (технологія мікрофон) для студентів інших команд стосовно свого матеріалу та задачу для самостійного домашнього розв’язування.

 

                  Оцінка знань та вмінь проводилася по рейтинговій системі. Максимальна кількість балів за всі етапи перевірки знань та вмінь – 50.

Кожен студент приймав участь у слідуючих етапах:

 

Етапи роботи	Максимальна кількість балів	Набрані бали
Участь в розв’язуванні  кросворду	5
Підбір матеріалу	5
Оформлення презентації	5
Демонстрація презентації	5
Бліцопитування	5
Оформлення буклету	5
Виконання тестових завдань	15
Додаткова участь	5
Підсумок	50

 

                Оцінка «12» виставляється, якщо студент набрав більше 50 балів.

                Оцінка «11» виставляється, якщо студент набрав 45-50 балів.

                Оцінка «10» виставляється, якщо студент набрав 40-44 бали.

                Оцінка «9» виставляється, якщо студент набрав 35-39 балів.

                Оцінка «8» виставляється, якщо студент набрав 30-34 бали.

                Оцінка «7» виставляється, якщо студент набрав 25-29 балів.

                Оцінка «6» виставляється, якщо студент набрав 20-24 бали.

                Оцінка «5» виставляється, якщо студент набрав 15-19 балів.

                Оцінка «4» виставляється, якщо студент набрав 10-14 балів.

                Оцінка «3» виставляється, якщо студент набрав 5-9 балів.

                Оцінка «2» виставляється, якщо студент набрав менше 5 балів.

 

Бали знімалися в наступних випадках:

1. Участь в розв’язуванні  кросворду

1.1 Невірна відповідь на запитання – 5 балів

1.2 Неточна відповідь – 3 бали

2. Підбір матеріалу

2.1 Неповні теоретичні викладки – 3 бали

2.2 Порушена лаконічність теоретичних викладок - 3 бали

2.3 Невдало підібрані задачі, або помилка в задачі – 4 бали

2.4 Відсутні запитання для опитування – 4 бали

2.5 Невдало підібрані запитання для опитування - 3 бали

2.6 Відсутня задача для самостійного розв’язування – 3 бали

3. Оформлення презентації

3.1 Порушена наочність у викладенні матеріалу – 3 бали

3.2 Порушена послідовність – 3 бали

3.3 Слайди перевантажені текстовою інформацією - 3 бали

3.4 Відсутнє гіперпосилання – 1 бал

3.5 Відсутнє посилання на джерела інформації – 3 бали

3.6 Відсутня інформація про авторів – 3 бали

4. Демонстрація презентації
   • 4.1. Відсутнє або некоректне пояснення до слайдів – 5 балів
   • 4.2. Допущена несуттєва помилка в поясненнях – 2 бали
   • 4.3. Порушена чіткість, лаконічність, послідовність пояснень – 3 бали
   •  
5. Бліцопитування

     Опитування.

• 5.1. Нечітко, неоднозначно сформульоване запитання – 2 бали.
• 5.2. Пропущена помилка у відповіді – 2 бали.
• 5.3. Недоповнена відповідь (у випадку, якщо вона була неповною) – 2 бали.

      Відповідь.

• 5.4. Відсутня відповідь на запитання – 5 балів.
• 5.5. Неповна, неточна відповідь на запитання – 3 бали.
•  

6. Оформлення буклету.

6.1 Недостатня інформативність – 3 бали

6.2 Порушена наочність у викладенні матеріалу – 2 бали

6.3 Порушена послідовність у викладенні матеріалу – 2 бали

6.4 Матеріал викладено «сухо», нецікаво –  2 бали

6.5 Відсутній девіз команди – 1 бал

6.6 Відсутнє посилання на джерела інформації – 3 бали

6.7 Відсутня інформація про авторів – 3 бали

 

7. Виконання тестових завдань
   • 7.1. Відсутня відповідь на одне запитання –  5 балів.
   • 7.2. Невірна відповідь на одне запитання –  5 балів.  
   • 7.3. Невчасно здана робота – 15 балів

 

Дидактичною метою проведення такого заняття було: 

забезпечити педагогічні умови для поглиблення і закріплення знань студентів з теми «Інтеграл та його застосування», набутих під час аудиторних занять та у процесі вивчення навчальної інформації, що виноситься на самостійне опрацювання;

спонукати студентів до колективного творчого обговорення найбільш складних питань навчального курсу, активізація їх до самостійного вивчення наукової та методичної літератури, формування у них навичок самоосвіти;

оволодіння методами аналізу фактів, явищ і проблем, що розглядаються та формування умінь і навичок до здійснення різних видів майбутньої професійної діяльності.

інтеграція сучасних педагогічних та інформаційних технологій підготовки майбутнього фахівця як соціально-адаптованої особистості відповідно до сучасних вимог ринку праці.

 

 

 

 

 

 

 

Формування професійних компетенцій за допомогою математичного моделювання продовжуємо і в роботі математичного гуртка.

Цього року гуртківці працювали над проектом «Математичне моделювання у  моїй професії та повсякденному житті» за графіком:

 

Графік проведення гуртка.

на І семестр 2014-2015 н.р.

(середа, по знаменнику, 14¹⁵, ауд.304)

 

№	дата	тема
1	10.09	Вступ. Презентація дослідницького проекту: «Історичний калейдоскоп» та «Видатні математики України».
2	24.09	Пошук форм реалізації про­екту: «Математичне моделювання у моїй професії та повсякденному житті». План роботи над проектом. Розподіл обов’язків.
3	08.10	Доповідь на тему: «Математика виникла з практичних потреб людства» - історична довідка.
4	22.10	Консультації по підбору практичних задач повсякденного життя для роботи над проектом.
5	05.11	Круглий стіл по розв’язуванню практичних задач повсякденного життя, відібраних студентами для роботи над проектом.
6	19.11	Систематизація відібраного матеріалу, обговорення форм його оформлення.
7	03.12	Видання математичної газети: «Математичне моделювання у  повсякденному житті»
8	17.12	Створення презентації : «Математичне моделювання у  повсякденному житті».

 

 

 

Графік проведення гуртка.

на ІІ семестр 2014-2015 н.р.

(середа, по знаменнику, 14¹⁵, ауд.304)

 

№	дата	тема
1	14.01	Консультації по підбору практичних задач обраної професії для роботи над проектом.
2	28.01	Підготовка студентів до участі в І турі Всеукраїнської студентської олімпіади з математики.
3	11.02	І тур Всеукраїнської студентської олімпіади з математики.
4	25.02	Інтелектуальна гра з математики: «Еврика»
5	11.03	Круглий стіл по розв’язуванню практичних задач обраної професії, відібраних студентами для роботи над проектом.
6	25.03	Доповідь: «Математичне моделювання в професії технолога»
7	08.04	Доповідь: «Математичне моделювання в професії соціолога»
8	22.04	Доповідь: «Математичне моделювання в професії механіка»
9	06.05	Доповідь: «Математичне моделювання в професії нафтовика»
10	20.05	Видання математичної газети: «Математичне моделювання у  моїй професії»
11	03.06	Створення презентації: «Математичне моделювання у  моїй професії та повсякденному житті».
12	17.06	Оформлення альбому-презентації дослідницького проекту з  математики: «Математичне моделювання у  моїй професії та повсякденному житті».  Виставка альбомів, рефератів, газет, моделей .

 

 

 

 

 

Висновки.

Мета навчання математики в нашому коледжі полягає в тому, щоб студент, по-перше, отримав фундаментальну математичну підготовку відповідно до програми, а по-друге, опанував навички математичного моделювання в області майбутньої професійної діяльності.

Фундаментальна математична підготовка випускника є основою для його майбутнього професійного життя, так як саме фундаментальні знання забезпечують випускникові можливість розуміти й освоювати нову техніку і технології, нові принципи організації виробництва.

Навички математичного моделювання можна розглядати як навички застосування математичних знань на практиці, а значить, у формуванні професійних компетенцій випускника. Математичне моделювання прикладних задач за фахом дозволяє поєднати теоретичні знання студентів з їх потребами, дає можливість шукати шляхи розширення застосування теоретичних знань у майбутній спеціальності безпосередньо в процесі навчання. Завдання, які мають прикладну спрямованість, формують у студентів стиль мислення, необхідний фахівцеві середньої ланки, а так само вміння оцінювати отриманий результат, прогнозувати результат експерименту, порівнювати, аналізувати різні ситуації, контролювати правильність отриманих висновків, оцінювати ступінь їх обгрунтованості.

Найважливішим із засобів забезпечення прикладної спрямованості у викладанні математики та математичного моделювання є реалізація міжпредметних зв'язків. Знання з математики являются базовими для різних спеціальностей, так як суттєво використовуються при вивченні ряду інших дисциплін. В результаті студенти:

- Використовують знання, вміння та навички, отримані на заняттях математики в практичній діяльності

- Навчаться ставити цілі і планувати діяльність по їх досягненню

- Освоюють комунікативний, аналітичний, творчий типи діяльності

- Набувають  навички роботи з довідковою літературою та іншими інформаційними носіями

- Адекватно оцінюють діяльність товаришів і свою

- Змінюють свою поведінку в колективі: прислухаються до думки іншої людини і без боязні висловлюють свою власну думку

У студентів формується уявлення про математику як про предмет, де кожному є можливість висловитися.

На своїх заняттях я сприяю розвитку таких якостей особистості молодих людей як готовність і здатність нести особисту відповідальність, як за власне благополуччя, так і за благополуччя суспільства.

 Таким чином, від якості математичної підготовки в значній мірі залежить рівень компетентності майбутнього фахівця. На мою думку, навчання математики має бути орієнтоване не стільки на отримання конкретних математичних знань і умінь у вузькому сенсі слова, скільки на освіту за допомогою математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Список  використаної  літератури

 1. Головань М. С. Компетенція і компетентність: досвід теорії, теорія досвіду / М. С. Головань // Вища освіта України. – 2008. – № 3. – С. 23–30.

2. Делор Жан. Сокрытое сокровище / Ж. Делор. – UNESCO, 1996. – 53 с.

3. Зимняя И. А. Социально-профессиональная компетентность как целостный результат профессионального образования: (идеализированная модель) / И. А. Зимняя // Проблемы качества образования. Компетентностный подход в профессиональном образовании и проектировании образовательных стандартов. – М.: Исследовательский центр проблем качества подготовки специалистов, 2005. – С. 10–20.

4. Матушанский Г. Модели подготовки и профессиональной деятельности специалистов / Г. Матушанский, А. Фролов // Высшее образование в России. – 2003. – № 4. – С. 92–95.

5. Моделирование деятельности специалиста на основе комплексного исследования / под ред. Е. Э. Смирновой. – Л.: Изд-во Ленингр. ун-та, 1984. – 176 с.

6. Татур Ю. Г. Компетентностный подход в описании результатов и проектировании стандартов высшего профессионального образования / Ю. Г. Татур // Материалы ко второму заседанию методологического семинара: авт. версия. – М.: Исследовательский центр проблем качества подготовки специалистов, 2004. – 23 с.

7. Татур Ю. Г. Компетентность в структуре модели качества подготовки специалиста / Ю. Г. Татур // Высшее образование сегодня. – 2004. – № 3. – С. 20–26.

8. Шадриков В. Д. Новая модель специалиста: инновационная подготовка и компетентностный подход / В. Д. Шадриков // Высшее образование сегодня. – 2004. – № 4. – С. 28–31.

9. Шуберт Ю. Ф., Андреещева Н. Н. Формирование у студентов профессиональных компетенций // Среднее профессиональное образование. – М., 2009. – № 12.

10. Якупова А. Р., Чернявская В. И. Компетентностная модель специалиста технического профиля // Научные исследования в образовании. Приложение к журналу «Профессиональное образование. Столица». – М., 2009. – № 6.

11. Рябченко В. Деякі концептуальні проблеми навчання і виховання студентів у сучасних вищих навчальних закладах Ураїни // Вища освіта України. – 2005. – №3. – С. 40-44.