Стаття на тему: "До питання використання комп’ютеру як засобу наочності"

До питання використання комп’ютеру як засобу наочності

Спрямованість  системи освіти на засвоєння знань, яка була традиційною і  виправданою ще декілька десятиліть тому, вже не відповідає соціальному замовленню, що вимагає виховання самостійних, ініціативних членів суспільства. Це потребує формування в учнів здатності діяти на основі здобутих знань, а не виконувати  лише дію за аналогією, за зразком.  Тому сучасні дидакти шукають такі засоби навчання, які б допомагали всім дітям фундаментально засвоїти навчальний матеріал, набути вміння самостійно вчитися, сприяли б їхньому розвиткові.

Одним із таких питань, яке на сучасному етапі вимагає перегляду і уточнення, є використання засобів наочності й моделювання у процесі формування знань і вмінь учнів.

Принцип наочності передбачає навчання на основі жи­вого сприймання конкретних предметів і явищ дійсності або їх зображень. Науковці виокремлюють наступні види наочності: натуральну (рослини, тварини, гірські породи, зоряне небо, прилади, машини, явища природи), образну (картини, таблиці, моделі, му­ляжі, математичні фігури), символьну (географічні кар­ти, графіки, діаграми, схеми, формули).

В педагогічній науці обгрунтовано, що використання наочності сприяє розумовому розвитку учнів, допомагає ви­явити зв'язок між науковими знаннями і життевою практикою, полегшує процес засвоєння знань, стимулює інтерес до них (розвиває мотиваційну сферу учнів), допо­магає сприймати об'єкт у розмаїтті його виявів і зв'язків.

Залежно від органів почуттів, наочні посібники поділяють на такі групи: фонічні (сприймаються слухом), візуальні (сприймаються зором) і змішані. До них належать: статичні посібники (діафільми, діапозитиви, посібники для епіопроекції); динамічні (кінофільми, кінофрагменти);  фонопосібники (грамзаписи, магнітофонні записи).

Використання наочності потрібно підпорядковувати конкретній меті, розвитку самостійності й активності уч­нів з урахуванням їх вікових особливостей. Наочність має бути змістовною, естетично оформленою, відповідати психоло­гічним законам сприймання, не повинна містити нічого зайвого і не викликати додаткових асоціацій, разом с тим, готуючи учнів до сприймання наочності, її не слід переоцінювати або недооцінювати у процесі навчання.

На практиці, зазвичай, використовують наступні способи подачі наочних посібників: безпосередня демонстрація, опосередкована демонстрація (за допомогою ТЗН), створення в процесі навчання таблиць, схем.

В педагогічних дослідженнях виділяють наступні функції наочності в залежності від дидактичної мети. Наочність виступає як:

1. джерело нових знань і уявлень про об'єкти, події, явища;
2. ілюстрація, яка служить опорою теоретичних положень;
3. спосіб розвитку мислення, що сприяє більш глибокому засвоєнню, розумінню зв'язку наукових знань з життям, що забезпечує міцність засвоєння знань, розвиток уваги, спостережливість, уявлення, а також абстрактного мислення, бо допомагає на основі розглянутих конкретних явищ прийти до узагальнень;
4. посібник для самостійної пізнавальної діяльності (в результаті порівняння, зіставлення учні набувають нових знань);
5. спосіб інструктажу;
6. спосіб повторення, повідомлення, систематизації;
7. спосіб контролю.

З розвитком технологій та інтересу молоді до них ефективним способом реалізації даних функцій стає використання інформаційно-комунікативних технологій, таких, як комп’ютер.

При вивченні математики зараз у досить широкому обсязі використовуються програми динамічної математики. Питання використання таких програм у процесі навчання математики учнів та майбутніх учителів математики досліджувала доктор педагогічних наук, професор Семеніхіна О. В. Науковець характеризує ці програми, як засоби комп’ютерної візуалізації математичних знань, що передбачають динамічне  оперування різними математичними, зокрема геометричними, об’єктами й можливість інтерактивного одержання відомостей про їх властивості. Основними характеристиками програм такого типу є:

•    інтерактивність;
•    динамічне оперування математичними моделями;
•    якісна візуалізація.

Дані програми мають доволі простий інтерфейс та не потребують багато часу для оволодіння ними та можуть допомогти учням, у яких недостатньо розвинена просторова уява.

Одним з відоміших представників програм динамічної математики є програма «Geogebra». GeoGebra — це вільний педагогічний програмний продукт, призначений для вивчення і викладання математики в середніх і вищих навчальних закладах, який поєднує динамічну геометрію, алгебру, математичний аналіз і статистику. Дана програма була розроблена в 2002 році як дипломний проект Маркуса Хохенватера під час навчання в університеті Зальцбурга і згодом стала міжнародним проектом, який розвивається стрімким темпом. Над ним працює інтернаціональна команда, яка налічує більше 20 розробників та понад 100 перекладачів.

Звісно використання даних програмних засобів не означає, що вчитель повинен перекласти всі завдання на комп’ютер. Використання подібних програм є ефективним тільки тоді, коли воно супроводжується словом учителя.

Відомий науковець Л.В.Занков обґрунтував раціональність наступних форм поєднання слова і наочності у навчальному процесі:

1.                         Вчитель за допомогою слова керує спостереженнями учнів, а знання про зовнішній вигляд предмета і його властивості й відношення учні здобувають самі у процесі спостереження.
2.                         Вчитель, спираючись на спостереження учнів і їх знання, підводить до осмислення таких зв'язків і явищ, які не можуть бути виявлені за допомогою безпосереднього сприйняття.
3.                         Вчитель за допомогою слова сам повідомляє учням відомості про предмет, його властивості, а наочні засоби служать підтвердженням, конкретизацією словесних повідомлень.
4.                         Учитель, ґрунтуючись на спостереженнях учнів, повідомляє про такі зв'язки між явищами, які недоступні безпосередньому спостереженню. Учні спостерігають тільки об'єкт, а вчитель сам узагальнює окремі дані, робить висновки про зв'язки між явищами, які безпосередньо не сприймаються учнями.

З урахуванням вищезазначеного вважаємо за доцільне використовувати комп’ютер як засіб наочності в «проблемних питаннях». Наприклад у процесі розв’язування завдань з параметрами.

Наведемо приклад використання програми GeoGebra у процесі розв’язування систем рівнянь другого порядку з параметром.

Завдання1: Установити, скільки розв’язків залежно від значень параметра має система рівнянь

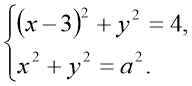
Дати відповідь на таке запитання аналітичними методами досить складно і потребує громіздких записів. Значно простіше це зробити графічно.

Створюємо динамічний малюнок за умовою (Рис.1). Графік першого рівняння будуємо у програмі GeoGebra, далі створюємо повзунок для зміни параметра і будуємо графік другого рівняння в залежності від .

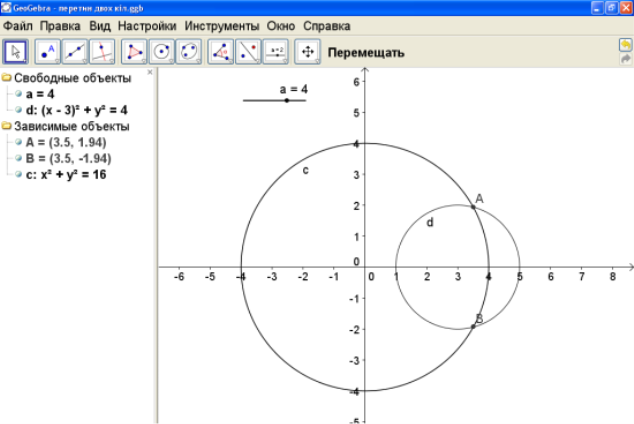
                                                                           Рис.1

Учитель коментує кожний крок побудов і динамічно змінюючи значення параметра підводить учнів до висновку про кількість розв’язків системи.

Відповідь:

система має один розв’язок

система має два розв’язки;

система не має розв’язків.

Завдання2: Установити, при яких значеннях параметра система рівнянь має рівно два розв’язки

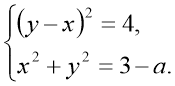
Змінюємо вже готовий динамічний малюнок у програмі GeoGebra просто замінивши рівняння на панелі об’єктів (Рис.2,3).

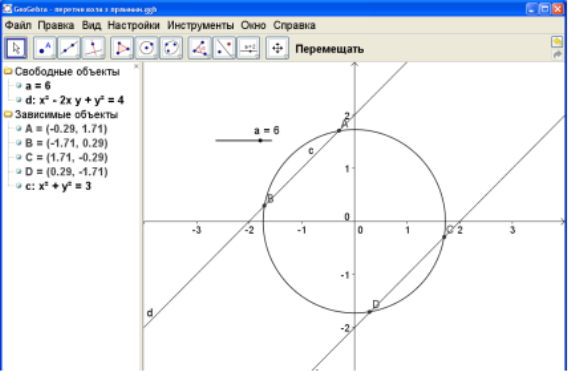
                                                                    Рис.2

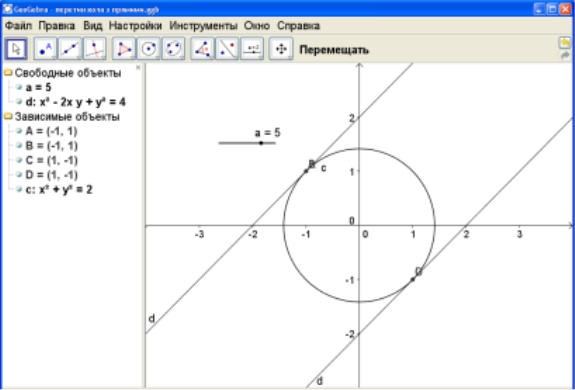
                                                                       Рис.3

Відповідь: система має два розв’язки при а=1

Отже, для встановлення кількості розв’язків системи рівнянь з двома змінними доцільно використовувати графічний спосіб, а якщо це можливо, то і використати програми динамічної математики.

Список використаних джерел

1. Сморжевський Л.О. Методика використання наочності на уроках алгебри і геометрії в основнній школі : навчальний посібник / Л.О. Сморжевський , Ю.Л. Сморжевський. Кам’янець-Подільський : Кам’янець-Подільський національний університет імені Івана Огієнка, 2010. – 184 с.
2. Раков С. А. Математична освіта : компетентнісний підхід з використанням ІКТ : монографія / С. А. Раков. – Х. : Факт, 2005. – 360 с.
3. Семеніхіна О.В., Друшляк М.Г. Обґрунтування доцільності використання програм динамічної математики як засобів комп’ютерної візуалізації математичних знань // Фізико-математична освіта. Науковий журнал. – 2015. – Випуск 3 (6). – С. 67-75.
4. Маркова Т. В. Использование интерактивной геометрической среды GeoNext и GeoGebra при обучении геометрии в 7–8 классах / Т. В. Маркова, Л. В. Тарасова, Н. Н. Куркова // Социальный компьютинг. – 2013. – № 1 (2). – С. 130–134.