Стаття "Нерівності як інструмент розв’язання ірраціональних рівнянь".

Нерівності як інструмент розв’язання

ірраціональних рівнянь.

              На перший погляд нерівності взагалі не мають ніякого відношення до розв’язання рівнянь. Дослідження нестандартних прийомів розв’язання саме ірраціональних рівнянь показали, що нерівності Коші, Коші-Буняковського  сприяють раціоналізації знаходження коренів заданого рівняння. Проблема в тому, що не до кожного рівняння ці нерівності можна застосувати. Розгляд конкретних прикладів дасть уяву до нестандартного прийому їх застосування. Як правило, ці нерівності застосовуються для 

1.  Застосування нерівності Коші

Теоретична викладка

Теорема  Якщо будь-які невід’ємні дійсні числа, то

Приклад 1.   Розв’язати рівняння

Розв’язання.

Розглянемо функції ,  ;

Застосовуємо до них нерівність Коші при

Оцінюємо суму функцій

Маємо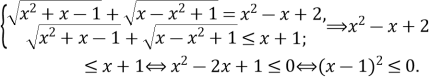

Знак «=» досягається при

Відповідь:  1.

Приклад 2.   Розв’язати рівняння

Розв’язання.

ОДЗ:

До правої частини рівняння застосуємо нерівність Коші при

Одержимо, що 

Знак «=» досягається при

Відповідь:  1.

Приклад 3.   Розв’язати рівняння

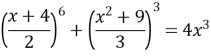
Розв’язання.

ОДЗ: З аналізу умови рівняння очевидно, що

Поділимо праву і ліву частини рівняння на (), одержимо

                                                                        (1)

Згідно нерівності Коші    

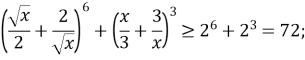
Що суперечить (1). Отже, задане рівняння не має коренів.

Відповідь: коренів не має.

Приклад 4.   Розв’язати рівняння

Розв’язання.

                                              (2)

До кожного виразу в дужках застосуємо нерівність Коші при

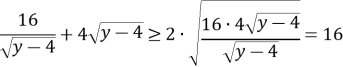
Рівність (2) досягається, якщо

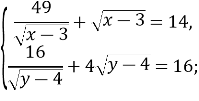
Розв’яжемо кожне з одержаних рівнянь системи окремо.

Заміна: одержимо

Заміна:маємо

Відповідь:  

2.   Застосування нерівності Коші-Буняковського

Теоретична викладка

Теорема  Якщо довільні дійсні числа, то

Рівність виконується, коли           

Приклад 1.   Розв’язати рівняння

Розв’язання.

ОДЗ: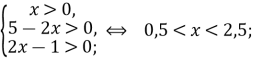    

       Застосовуємо до лівої частини заданого рівняння нерівність Коші-Буняковського при 

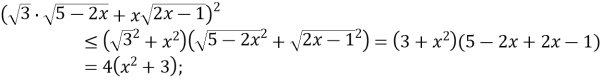
Рівність можлива лише за умови, якщо    , тобто

(3)

Оскільки сума коефіцієнтів рівняння (3) дорівнює нулю, то число 1 є коренем цього рівняння

Відповідь:  1.

Приклад 2.   Розв’язати рівняння

Розв’язання.

ОДЗ:   

        Застосовуємо до лівої частини заданого рівняння нерівність Коші-Буняковського при 

Згідно до умови заданого рівняння

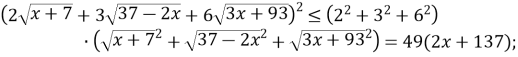
Рівність можлива лише за умови, якщо     = тобто

         Коренем першого рівняння є число  5, яке задовольняє друге та третє рівняння системи.

Відповідь:   5.

Приклад 3.   Розв’язати рівняння

Розв’язання.

ОДЗ: 

       Застосовуємо до лівої частини заданого рівняння нерівність Коші-Буняковського при 

Згідно до умови заданого рівняння

    тоді

Рівність можлива лише за умови, якщо    , тобто

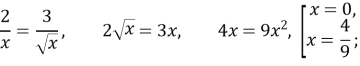
Числа  є коренями заданого рівняння.

Відповідь:  0,

         Очевидно, що застосування нерівностей Коші та Коші – Буняковського можна застосувати далеко не для кожного ірраціонального рівняння, проте знання цих прийомів збагатить арсенал прийомів, які можна «випробовувати» для знаходження коренів ірраціональних рівнянь, застосування загальноприйнятих прийомів до яких неприйнятне.