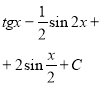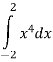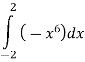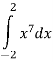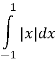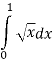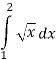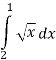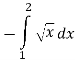Посібник для уроків алгебри І семестр 11 клас
Ківерцівська експериментальна школа
Навчальний посібник


___________________________________
___________________________________
Шановні одинадцятикласники!
Вам пропонується навчальний посібник, який ви будете використовувати на уроках алгебри.
Посібник складається з чотирьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких проводиться робота з засвоєння понять, термінів і правил блоку навчальної інформації, також наведені вправи і завдання для відпрацювання практичних умінь і навичок.
-
між уроками фронтального опрацювання ви будете виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені

- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен покаже свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Нехай Бог посилає вам мудрості у вивченні алгебри!!!
Тема №1. Інтеграл та його застосування
Урок №1

Інтеграл та його застосування
Нескінченність! Ніщо не
рухало так мудро розум людський
Д. Гільберт
Питання
- Первісна та її властивості. Таблиця первісних.
- Правила знаходження первісної (правила інтегрування)
- Визначений інтеграл. Формула Ньютона – Лейбніца.
- Застосування інтеграла.
Література
Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, §8 – 12, стор. 74 – 118.
|
1. Первісна та її властивості. Таблиця первісних |
|||||||||||||||||||||||||||||||||||||
|
1.1 |
Інтегруванням називають операцію, обернену до диференціювання, тобто знаходження функції за її похідною. |
||||||||||||||||||||||||||||||||||||
|
1.2 |
Функцію F(х) називають первісною для функції f(х) на заданому проміжку, якщо для всіх |
|
|||||||||||||||||||||||||||||||||||
|
1.3 |
Основна властивість первісної
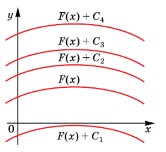
Кожна з первісних для функції |
Геометричний зміст Графіки будь – яких первісних даної функції можна отримати один з одного паралельним перенесенням уздовж осі ординат.
|
|||||||||||||||||||||||||||||||||||
|
1.4 |
Невизначеним інтегралом називають сукупність усіх первісних функції
Позначення:
|
|
|||||||||||||||||||||||||||||||||||
|
1.5
|
Таблиця первісних |
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
2. Правила знаходження первісної (правила інтегрування) |
|||||||||||||||||||||||||||||||||||||
|
2.6 |
Якщо функції F(х) і G(х) є відповідно первісними функцій f(х) і g(х), то Первісна для суми дорівнює сумі первісних для доданків |
Інтеграл від суми дорівнює сумі інтегралів від доданків |
|||||||||||||||||||||||||||||||||||
|
2.7 |
Якщо функція F(х) є первісною функції f(х) та k – деяке число, то |
Сталий множник можна виносити за знак інтеграла |
|||||||||||||||||||||||||||||||||||
|
2.8 |
Якщо функція F(х) є первісною функції f(х) та k – деяке число, відмінне від нуля, тоді |
|
|||||||||||||||||||||||||||||||||||
|
3. Визначений інтеграл. Формула Ньютона-Лейбніца |
|||||||||||||||||||||||||||||||||||||
|
3.9 |
Різницю |
0
|
|||||||||||||||||||||||||||||||||||
|
3.10 |
Формула Ньютона – Лейбніца
|
||||||||||||||||||||||||||||||||||||
|
3.11 |
Властивості визначених інтегралів:
|
||||||||||||||||||||||||||||||||||||
|
4. Застосування інтеграла |
|||||||||||||||||||||||||||||||||||||
|
4.12 |
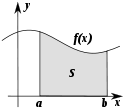
Фігуру, обмежену графіком функції f(х) і прямими
|
|
|||||||||||||||||||||||||||||||||||
|
4.13 |
Площу S криволінійної трапеції, обмеженої графіком функції
де F – будь - яка первісна функції f на відрізку |
||||||||||||||||||||||||||||||||||||
|
4.14 |
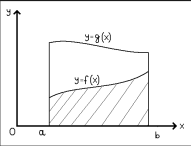
Якщо функції f і g є неперервними на відрізку
|
|
|||||||||||||||||||||||||||||||||||
Уроки №2 – 4
«Крапля довбає камінь не силою, а часто падаючи»
Джордано Бруно
Фронтальне опрацювання матеріалу
Первісна. Правила знаходження первісної
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.8 блоку № 1.
- Усно відповісти на питання:
-
Що називають первісною функції
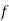 ?
?
- Як читається основна властивість первісної?
-
Який загальний вигляд первісних функції
 ?
?
- Що таке невизначений інтеграл?
- Чому дорівнює первісна суми функцій?
-
Чому дорівнює первісна функції
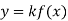 ?
?
-
Чому дорівнює первісна функції
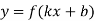 ?
?
Завдання 2.
Усно виконати вправу 8.1, стор. 76.
ІІ. Відпрацювання практичних умінь та навичок
Письмово виконати вправи з підручника, сторінки 76 – 78, ст. 86 – 89, :
Завдання 3.
8.5; 8.7; 8.11; 8.19.
Завдання 4.
9.7; 9.9; 9.13; 9.17; 9.23; 9.31, 9.29.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ
Завдання 5.
Частина 1.
Завдання 1–4 мають по 5 варіантів відповідей, із яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відповідь.
-
Знайти загальний вигляд первісної для функції
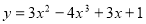 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
-
Знайти загальний вигляд первісної для функції
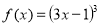 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайти загальний вигляд первісної для функції
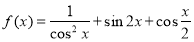 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
- Яке з тверджень є неправильним?
|
А |
Б |
В |
Г |
Д |
|
Операція знаходження первісної називається інтегруванням. |
Диференціювання і інтегрування обернені операції. |
Щоб знайти закон руху, треба про інтегрувати функцію, що виражає швидкість |
Первісною для функції |
Первісна добутку дорівнює добутку первісних. |
Частина 2.
У завданнях 5–6 наведіть розв’язання, запишіть відповідь.
-
Для функції
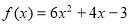 знайти первісну, графік якої проходить через точку
знайти первісну, графік якої проходить через точку 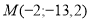 . У відповіді записати значення
. У відповіді записати значення 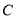 .
.
-
Швидкість руху точки задано рівнянням
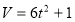 (м/с). Знайти рівняння руху
(м/с). Знайти рівняння руху 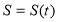 , якщо відомо, що в момент часу
, якщо відомо, що в момент часу 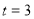 с точка знаходилась на відстані 42,8 м. У відповіді записати значення
с точка знаходилась на відстані 42,8 м. У відповіді записати значення 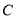 .
.
Частина 3.
Розв’язання завдань 7–8 повинно містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.
-
Знайти найменший додатний корінь рівняння
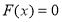 , якщо
, якщо 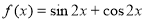 .
.
-
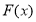 – первісна функції
– первісна функції 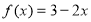 , графік якої має спільну точку з графіком функції
, графік якої має спільну точку з графіком функції 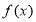 , що належить осі ординат. Знайти первісну
, що належить осі ординат. Знайти первісну 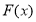 та всі точки перетину графіків функцій
та всі точки перетину графіків функцій 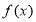 і
і 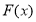 . У відповідь записати суму всіх координат точок перетину.
. У відповідь записати суму всіх координат точок перетину.
Уроки №5, 6
Жоден чоловік не може стати хорошим батьком,
поки він не навчиться розуміти свого батька.
Т. Вайлдер (американський письменник)
Фронтальне опрацювання матеріалу
Невизначений інтеграл
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.8 блоку № 1.
- Дайте відповіді на питання:
- Що називають інтегруванням?
- Дайте визначення первісної.
- Дайте визначення невизначеного інтегралу.
- Який загальний вигляд первісної?
- Назвіть первісні для функцій:
1) х7; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4)![]() ; 5)
; 5) ![]() ; 6) cos х; 7) sin х;
; 6) cos х; 7) sin х;
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Установіть відповідність між функціями (1 – 4) і первісними (А – Д), графіки яких проходять через точку М:
![]() 3)
3) ![]()
![]() ; 4)
; 4) ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання 3.
-
Знайдіть
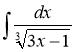
- Знайдіть загальний вигляд первісних для функцій:
1) f(x) = 2х5 - 5х2; 2) f(x) = ![]() + 3
+ 3![]() .
.
3.3. Знайдіть загальний вигляд первісних для функцій:
1) f(x)=5cosх – 3sin x; 2) f(x)= 3cos x.
Завдання 4.
4.1. Знайдіть невизначені інтеграли:
1) ![]() ; 2)
; 2) 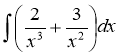 ; 3)
; 3) ![]() .
.
4.2. Знайдіть невизначені інтеграли:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 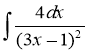 ;
;
4.3. Знайдіть загальний вигляд первісних для функцій:
-
f(x) = 1 – cos 3х; 2) f(x) = – 2cos 6x; 3) f(x) =
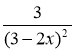 .
.
Урок №7
«Навчання ніколи не вичерпує розум»
Леонардо да Вінчі
Фронтальне опрацювання матеріалу
Первісна. Правила знаходження первісної. Невизначений інтеграл
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.8 блоку № 1.
- Дайте відповіді на питання:
- Що називають інтегруванням?
- Дайте визначення первісної.
- Дайте визначення невизначеного інтегралу.
- Який загальний вигляд первісної?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно розв’яжіть вправи:
-
Знайдіть загальний вигляд первісної для функції
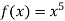 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
-
Вкажіть загальний вигляд первісної для функції
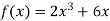 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
-
Знайдіть
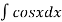 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
Завдання 3.
Письмово розв’яжіть вправи:
-
Знайдіть загальний вигляд первісних для функцій: 1)
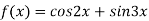 ; 2)
; 2) 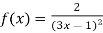 .
.
- Установіть відповідність між функціями (1 – 4) і первісними (А – Д), графіки яких проходять через точку М:
-
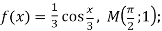 3)
3) 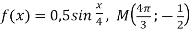
-
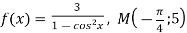 ; 4)
; 4) 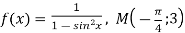
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайдіть невизначені інтеграли: 1)
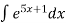 ; 2)
; 2) 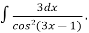
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
1. Знайдіть загальний вигляд первісних для функцій: 1) ![]() ; 2)
; 2) ![]() .
.
-
Знайдіть невизначені інтеграли: 1)
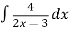 ; 2)
; 2) 
Уроки №9 – 11
«Працьовитість – душа
будь-якої справи і запорука добробуту»
Чарльз Діккенс
Фронтальне опрацювання матеріалу
Визначений інтеграл. Формула Ньютона – Лейбніца
І. Засвоєння термінології до теми
Завдання 1.
- Повторити тези 3.9 – 3.11 блоку № 1.
- Усно відповісти на питання:
- Що називають визначеним інтегралом функції на відрізку?
- Як обчислити значення визначеного інтеграла?
- Сформулювати властивості визначеного інтеграла.
ІІ. Відпрацювання практичних умінь і навичок
Завдання 2.
Розгляньте наступний приклад розв’язування вправи:
Обчисліть інтеграл ![]() .
.
Розв’язання. Для функції ![]() однією з первісних є
однією з первісних є ![]() . Маємо за формулою Ньютона-Лейбніца
. Маємо за формулою Ньютона-Лейбніца
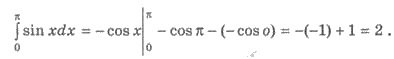
Завдання 3.
Письмово виконати вправи, стор. 97 – 99 підручника: 10.7; 10.13; 10.22.
Завдання 4.
Письмово виконати вправи, стор. 105 – 107 підручника: 11.2 (1 , 3); 11.4 (2, 4); 11.6 (1, 2); 11.12; 11.14; 11.20.
ІІІ. Відпрацювання умінь розв’язування вправ, які пропонуються на ЗНО
Завдання 5.
Завдання з вибором однієї правильної відповіді.
- Укажіть інтеграл, значення якого є додатним числом.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Укажіть інтеграл, значення якого є додатним числом.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Укажіть інтеграл, значення якого належить проміжку
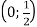 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайдіть
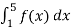 , якщо
, якщо 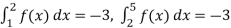 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
0 |
3 |
6 |
- Які з наведених тверджень є правильними?
І. ![]() .
.
ІІ. ![]() .
.
ІІІ. ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
Тільки І |
Тільки ІІ |
Тільки ІІІ |
Тільки І і ІІ |
Усі твердження |
- Які з наведених тверджень є НЕПРАВИЛЬНИМИ?
І. ![]()
ІІ. ![]() .
.
ІІІ. ![]()
|
А |
Б |
В |
Г |
Д |
|
Тільки І |
Тільки ІІ |
Тільки ІІІ |
Тільки ІІ і ІІІ |
Усі твердження |
Завдання 6.
Завдання з короткою відповіддю (розв’яжіть завдання і запишіть відповідь ОДНИМ ЧИСЛОМ).
-
Обчисліть інтеграл
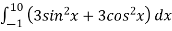 .
.
-
Обчисліть інтеграл
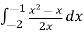 .
.
-
Обчисліть інтеграл
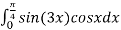 .
.
-
Обчисліть інтеграл
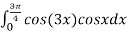 .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Знайдіть значення інтегралів:
1 ![]() 2
2 ![]() 3
3 ![]() 4
4 ![]()
-
Обчисліть інтеграл:
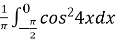 .
.
Уроки №13 – 16
«Не будь нахабний i не вважай
недосконалим те, що тобі незрозуміле»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Обчислення площ плоских фігур
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.9 – 4.14 блоку № 1.
- Усно дати відповідь на питання:
- Що називають визначеним інтегралом?
- Записати на дошці формулу Ньютона – Лейбніца
- Перерахувати властивості визначених інтегралів.
- Що називають криволінійною трапецією?
- За якою формулою можна обчислити площу криволінійної трапеції?
-
За якою формулою можна обчислити площу фігури, обмеженої графіками функцій
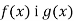 та прямими
та прямими 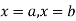 ?
?
ІІ. Відпрацювання практичних умінь та навичок
Письмово розв’язати вправи з підручника, стор. 113 – 114:
Завдання 3.
12.2; 12.6 (1, 3, 5).
Завдання 4.
12.10, 12.11.
Завдання 5.
Обчислити площу фігури, обмеженої лініями:
5.1. ![]()
5.2. ![]()
5.3.![]()
5.4. ![]()
5.5. ![]()
5.6. ![]()
5.7. ![]()
-
прямою
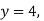 параболою
параболою 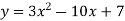 і дотичною до цієї параболи, проведеною через точку з абсцисою
і дотичною до цієї параболи, проведеною через точку з абсцисою  .
.
Урок №17
«Слухай ради й картання приймай,
щоб мудрим ти став при своєму кінці»
Приповісті Соломонові 19:20
Фронтальне опрацювання матеріалу
Застосування інтеграла до розв’язування прикладних задач
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
-
Записати у блок № 1 формулу для обчислення об’єму тіла обертання: коли при обертанні фігури, обмеженої графіком неперервної та невід’ємної на відрізку
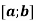 функції f і прямими
функції f і прямими 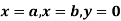 , навколо осі абсцис утворюється тіло об’єму V, то
, навколо осі абсцис утворюється тіло об’єму V, то 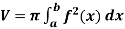 .
.
-
Записати у блок № 1 приклади застосування інтеграла у фізиці:
-
Обчислення шляху за відомим законом зміни швидкості за інтервал часу від
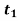 до
до 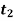 :
: 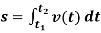 ;
;
-
Обчислення маси неоднорідного стержня на відрізку
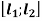 :
: 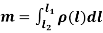 .
.
-
Обчислення кількості електрики, яка проходить через поперечний переріз провідника за час від
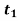 до
до 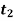 :
: 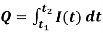 .
.
-
Обчислення шляху за відомим законом зміни швидкості за інтервал часу від
- Записати у блок № 1 приклади застосування інтеграла в економіці і техніці:
обсяги випуску або витрат продукції: ![]() , де t – робочий час,
, де t – робочий час, ![]() - функція, що виражає продуктивність праці.
- функція, що виражає продуктивність праці.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконати вправи:
- Вправа 12.8 стор. 114.
-
Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом
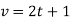 (м/с). Знайти шлях, який пройшло тіло за інтервал часу від
(м/с). Знайти шлях, який пройшло тіло за інтервал часу від 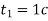 до
до 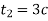 .
.
-
Знайти масу стержня завдовжки 35 см, якщо його лінійна густина змінюється за законом
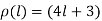 кг/м.
кг/м.
-
Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом
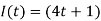 А.
А.
-
Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою
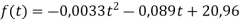 , де t – робочий час у годинах. Обчислити обсяг випуску продукції, за квартал вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
, де t – робочий час у годинах. Обчислити обсяг випуску продукції, за квартал вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Обчисліть площу фігури, обмеженої лініями:
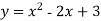 та
та 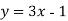 .
.
-
Обчисліть площу фігури, обмеженої лініями:
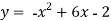 та
та 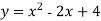 .
.
Урок №19
«Хоча б над тобою було сто вчителів –
вони будуть безсилі, якщо ти не зможеш сам
змусити себе до праці і сам вимагати її від себе»
В. Сухомлинський
Внутрішньопредметне узагальнення матеріалу
Інтеграл та його застосування
І. Засвоєння термінології до теми
Завдання 1.
- Повтори блок № 1. Особливу увагу зверни на тези 1.2 – 2.9, 3.11, 4.13, 4.14.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Вкажи первісну для функції
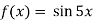 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
-
Обчисли
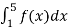 , якщо
, якщо 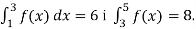
|
А |
Б |
В |
Г |
Д |
|
1 |
3 |
14 |
5 |
7 |
-
Запиши формулу для обчислення площі фігури, обмеженої лініями
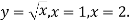
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Інша відповідь |
Завдання 3.
Письмово виконай вправи:
-
Для функції
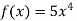 знайди первісну, графік якої проходить через точку
знайди первісну, графік якої проходить через точку 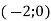 .
.
-
Знайди загальний вигляд первісної для функції: 1)
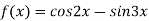 ; 2)
; 2) 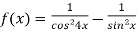 .
.
-
Обчисли інтеграл: 1)
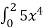 ; 2)
; 2)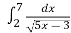 .
.
-
Обчисли площу фігури, обмеженої лініями
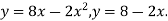
Тема №2. Показникова функція
Урок №1

Показникова функція
«…жодне з інших понять не відображає явищ
реальної дійсності з такою безпосередністю і з такою
конкретністю, як поняття функціональної залежності…»
О.Я.Хінчин, радянський математик
Питання
- Показникова функція, її графік та властивості
- Основні показникові тотожності
- Розв’язування найпростіших показникових рівнянь і нерівностей
Література
Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, §1 – 3, стор. 6 – 31.
|
1. Показникова функція, її графік та властивості |
||
|
1.1 |
Показниковою називається функція виду |
|
|
1.2 |
Властивості показникової функції
функція набуває лише додатних значень графік не перетинає вісь Ох);
3)Якщо
перетинає вісь 4)Зростає на всій числовій прямій,
5)Якщо |
|
|
2. Основні показникові тотожності |
||
|
2.3 |
1)
5) |
|
|
3. Розв’язування найпростіших показникових рівнянь і нерівностей |
||
|
3.4 |
Рівняння (нерівності), в яких невідоме входить до показника степеня, називають показниковими
|
|
|
3.5 |
Властивості показникових рівнянь і нерівностей:
1. Якщо
2. Якщо
|
|
|
3.6 |
Основні способи розв’язування показникових рівнянь та нерівностей 1) зведення до однієї основи; 2) винесення спільного множника за дужки; 3) ділення обох частин на степінь; 4) зведення до квадратного шляхом заміни |
|
Урок №2
«І все, що тільки чините,
робіть від душі, як Господу, а не людям»
Послання св. апостола Павла до Колосян 3 : 23
Фронтальне опрацювання матеріалу
Степінь з дійсним показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.3 блоку №2.
- Дайте відповіді на питання:
- Що називається n-им степенем числа a при натуральному n?
- Дайте визначення степеня з цілим від’ємним показником; степеня з нульовим показником.
- Дайте визначення степеня з раціональним показником.
Завдання 2.
2.1. Обчисліть ![]() .
.
2.2. Запишіть у вигляді степеня вираз:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
Завдання 3.
Розгляньте приклад розв’язування вправи:

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
4.1. Обчисліть:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
4.2. Спростіть вираз:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
4.3. Виконайте вправу 1.6; 1.12, 1.20 ст. 13, 14.
Уроки №3,4
«Хто з мудрими ходить, той мудрим стає,
а хто товаришує з безумним, той лиха набуде»
Книга приповістей Соломонових 13:20
Фронтальне опрацювання матеріалу
Показникова функція, її графік і властивості
І. Робота над засвоєнням понять, термінів і правил
Завдання 1
- Повторити тези 1.1 – 2.3 блоку № 2.
- Усно дати відповідь на питання:
- Що називається показниковою функцією?
- Перерахувати властивості показникової функції.
- Записати основні показникові тотожності.
Завдання 2
Усно виконати вправи:
-
Укажіть, які із заданих функцій зростають, а які спадають: 1)
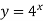 ; 2)
; 2) 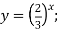 3)
3) 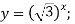 4)
4) 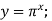 5)
5) 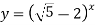 .
.
-
Знайдіть область значень функції: 1)
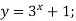 2)
2) 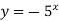 ; 3)
; 3) 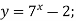 4)
4) 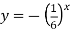 .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Побудуйте графік функції: 1)
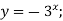 2)
2) 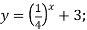 3)
3) 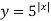 ; 4)
; 4) 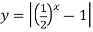
-
Порівняйте значення виразів: 1)
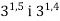 ; 4)
; 4) 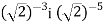 ; 7)
; 7) 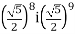 ;
;
2) ![]() ; 5)
; 5) ![]() ; 8)
; 8) ![]() ;
;
3) ![]() ; 6)
; 6)![]() ; 9)
; 9) ![]()
- Порівняйте показники m і n, коли відомо, що є правильною нерівність
1) ![]() ; 4)
; 4) ![]() 7)
7) ![]()
2) ![]() 5)
5) ![]() 8)
8) ![]()
3) ![]() 6)
6) ![]()
- Порівняйте з одиницею додатну основу а, коли відомо, що є правильною нерівність:
1) ![]() ; 3)
; 3)![]() ; 5)
; 5)![]() ;
;
2)![]() ; 4)
; 4)![]() ; 6)
; 6)![]() ;
;
- Розташуйте числа у порядку їх зростання:
1) ![]() ,
, ![]() ,
,![]() ,
, ![]() 1;
1;
2) ![]() , 1,
, 1, ![]() .
.
Уроки №5, 6
Мало знати, потрібно й використовувати.
Мало бажати, потрібно й робити.
Й. Гете
Фронтальне опрацювання матеріалу
Показникові рівняння і нерівності
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 3.6 блоку № 2.
- Усно дати відповідь на питання:
- Яка функція називається показниковою?
- Яка область визначення функції у = 0,1х ?
- Яка область визначення показникової функції?
- Яка область значень показникової функції?
- При якій умові показникова функція є зростаючою?
- При якій умові показникова функція є спадною?
- Яке рівняння називають показниковим?
- Назвіть основні способи розв’язування показникових рівнянь.
Завдання 2.
Усно виберіть правильну відповідь:
- Які з наведених функцій є показниковими?
1) у = 3х; 2) у = х3; 3) у = 1х;
4) у = (-4)х; 5) у = ![]() ; 6) у = х0,6;
; 6) у = х0,6;
7) у = (х – 5)8; 8) у = (1 - ![]() )х; 9) у = 9х;
)х; 9) у = 9х;
10) у = х-х; 11) у = πх; 12) у = ![]() .
.
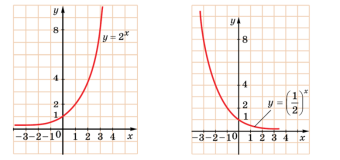
- Які з наведених графіків є графіками показникової функції?
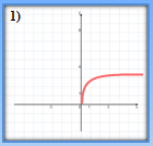
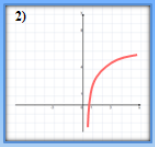
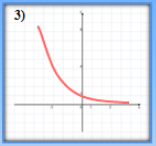
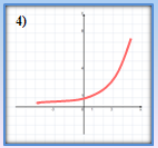
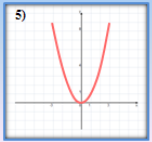
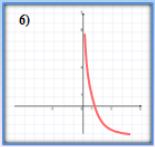
- Серед наведених функцій виберіть ті, що зростають.
- у = 2х ; 2) у =100,5х ; 3)у =0,65х+2 ; 4) у = 0,151,5х;
5) у![]() ; 6) у =
; 6) у =![]() .
.
- Серед наведених функцій виберіть ті, що спадають.
1) у = 40,3х ; 2) у = 0,3х ; 3) у = 6,92х-1 ;4) у = 0,112х ;
5) у = ![]() ; 6
; 6![]() у
у![]() 7) у =
7) у =![]()
5. Встановіть відповідність:
-
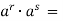
-
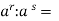
-
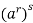 =
=
-
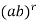 =
=
-
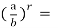
- a0 =
- а1 =
-
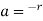
А) ![]()
Б) ![]()
B) 1
Г) ![]()
Д) а
Е) ![]()
Є) ![]()
Ж) ![]()
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3
Письмово виконати вправи:
- Розв’язати рівняння:
1) 2х∙3х = 36;
2) 4х+ 2х+1 = 80;
3) 52х+1 – 52х-1 = 24.
-
Розв’язати нерівність:
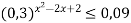 .
.
- Розв’язати рівняння 3∙16х + 2∙81х = 5∙36х.
-
Розв’яжіть рівняння
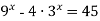 .
.
-
Розв’яжіть систему рівнянь
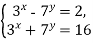
Завдання 4.
Письмово виконати вправи 2.17 (1, 3), 2.19; 2.33 ст. 22 – 23.
Урок №7
«Чим додержить юнак у чистоті
свою стежку? – Як держатиметься Твоїх слів!»
Псалом 118:9
Фронтальне опрацювання матеріалу
Показникові рівняння і нерівності
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 3.6 блоку № 2.
- Усно дати відповідь на питання:
- Яка функція називається показниковою?
- Перерахувати властивості показникової функції.
- Які рівняння (нерівності) називаються показниковими?
- Перерахувати властивості показникових рівнянь і нерівностей?
- Перерахувати основні способи розв’язування показникових рівнянь та нерівностей.
Завдання 2.
Усно розв’язати вправи:
-
Обчислити значення виразу
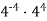 .
.
|
А |
Б |
В |
Г |
Д |
|
|
0 |
|
1 |
|
-
Розв’яжіть рівняння
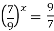 .
.
|
А |
Б |
В |
Г |
Д |
|
0 |
1 |
|
– 1 |
3 |
-
Розв’яжіть нерівність
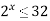 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконати вправи:
-
Побудуйте графік функції: 1)
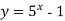 ; 2)
; 2) 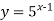 .
.
-
Порівняйте значення виразів: а)
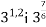 ; б)
; б) 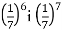 .
.
-
Розв’язати рівняння
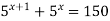 ;
;
-
Розв’язати нерівність
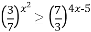
-
Розв’язати рівняння: а)
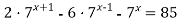 ; б)
; б) 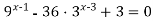 .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Побудуйте графік функції
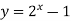 .
.
-
Порівняйте значення виразів: а)
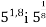 ; б)
; б) 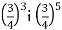 .
.
-
Розв’язати рівняння
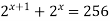 ;
;
-
Розв’язати нерівність
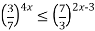 .
.
-
Розв’язати рівняння: а)
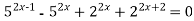 ; б)
; б) 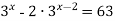 .
.
Урок №9
«Бо що тільки людина посіє, та саме й пожне!»
Послання до галатів 6:7
Внутрішньопредметне узагальнення матеріалу
Показникова функція
І. Засвоєння термінології до теми
Завдання 1.
- Повторити блок № 2.
- Письмово відповісти на питання, запропоновані вчителем.
- Усно розв’язати вправи:
-
Обчислити значення виразу
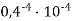 .
.
|
А |
Б |
В |
Г |
Д |
|
256 |
2,56 |
|
0,256 |
25,6 |
-
Розв’яжіть рівняння
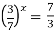 .
.
|
А |
Б |
В |
Г |
Д |
|
0 |
1 |
|
– 1 |
3 |
-
Укажіть проміжок, якому належить корінь рівняння
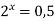 .
.
|
А |
Б |
В |
Г |
|
(–2; –1) |
(–1;0) |
(0; –1) |
|
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Письмово розв’язати вправи:
-
Порівняти числа
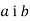 , якщо: 1)
, якщо: 1) 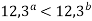 ; 2)
; 2) 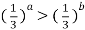 .
.
-
Розв’язати нерівність:
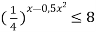 .
.
-
Розв’язати рівняння
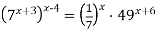 .
.
-
Розв’язати рівняння:
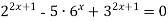
-
Розв’язати рівняння
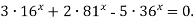
1


про публікацію авторської розробки
Додати розробку