Стаття "Про деякі методи розв’язування стереометричних задач".

                                                                              Ольга Овчар, вчитель математики

                                                                 вищої категорії сзш №67 м.Львова

       Про деякі методи розв’язування стереометричних задач.

В статті висвітлено питання розв’язування задач на перших уроках стереометрії в 10 класі..

Постановка проблеми. Формування навиків пошуку розв’язування задач, доведень теорем розглядається як один з основних аспектів навчально-виховного процесу. Учням цікавий сам процес пошуку, в них пробуджується інтерес.

      Проблеми пошуку розв’язків  задач хвилюють як вчителів, так і методистів та вчених. З цього приводу написано багато книг і статтей. Однак, не можна сказати, що ця проблема повністю розв’язана в школі.

     Приступаючи до розв’язування, учень інтуїтивно шукає зв’язки між відомими елементами задачі і шуканими. Як правило, цей пошук ведеться хаотично. Просторові уявлення в багатьох десятикласниках розвинуті ще слабо. Досвід показує, що пошук розв’язків у цьому випадку сприяє попередній розгляд моделі до задачі. Учні швидше справляються з побудовою рисунка, глибше розуміють його особливості. Завдання вчителя заключається в тому, щоб систематизувати пошук розв’язку, привчати учнів аналізу умови. Перше, на що слід звернути увагу, це вимога задачі. Після цього учні разом з учителем складають схему розв’язування (це може бути короткий запис, скорочений схематичний запис та інше). Потім іде самостійне розв’язування задачі учнями.

     Досвід показує, що на перших уроках на пошук розв’язку і складання схеми на уроці затрачається стільки часу, скільки і на саме розв’язування. Доцільно після повного розв’язку однієї задачі зробити аналіз 2-3 задач, накреслити шляхи їх розв’язування. Розв’язавши багато задач, учні набувають навиків розумової діяльності і знайомляться з такою діяльністю (аналіз, синтез, порівняння, узагальнення), надалі набагато швидше справляються з пошуками розв’язків.  

Мета статті. Ознайомити з деякими методами розв’язування задач при вивченні перших розділів стереометрії.

Виклад основного матеріалу. При переході до вивчення стереометрії в учнів часто виникають великі проблеми, особливо при розв’язуванні завдань з перших розділів. Учні відчувають великі труднощі при виконанні рисунків. Невміння зображати взаємне розміщення заданих точок, прямих і площин викликає розгубленість учнів, веде до хибних розв’язків.

Наведу деякі рекомендації, які допомагають учням при вивченні перших розділів стереометрії:

1. підводити учнів до того, щоби деякі фігури розміщувати в одній площині;
2. ті фігури, які не можна розмістити у вибраній площині, слід розміщувати певним способом відносно неї. Цю площину найкраще зображати горизонтально;
3. вибирати площину за умовою задачі: дві прямі, що перетинаються, пряму і точку поза нею, дві різні паралельні прямі і т.д.;
4. необхідно, щоб  учні запам’ятали, що перпендикулярність прямих l₁ і l₂ в просторі означає перпендикулярність прямої l₁ деякій площині α, якій належить пряма l₂, або пряма l₂ перпендикулярна площині β, якій належить пряма l₁. [1]

Задача 1.  В просторі дано прямі l₁ і l₂  і точка М,  яка не належить жодній прямій. Через точку М провести пряму l, перпендикулярну прямим l₁ і  l₂.

Для розв’язування задачі необхідно уявити розміщення в просторі двох мимобіжних ( в загальному вигляді) прямих l₁ і l₂ і  точки М, яка не належить жодній з прямих.                                                                                                                                                        

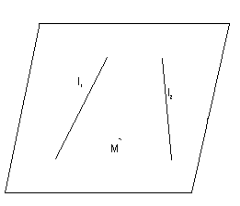За рис.1 важко знайти розв’язок задачі. На практиці

             учнів слід підводити до того, щоби вони вміли застосовувати раніше дані рекомендації. В даній задачі вибираємо площину, яка може проходити через задані в умові дві прямі, які перетинаються, пряму і точку поза нею, дві різні

рис.1                                                                                                                                2

паралельні прямі і інше. Якщо дані мимобіжні прямі, то їх зручно розміщувати на двох паралельних площинах. Виходячи з такого розміщення фігур, можна зробити так, є дві  паралельні площини, на яких розміщенні дві мимобіжні прямі l₁ і l₂ . Пряма перпендикулярна до двох прямих, перпендикулярна і даним площинам. Слід  звернути увагу, що перпендикулярні прямі у просторі учні вважають як такі, що перетинаються,         

а це приводить до помилкових висновків. Вони повинні засвоїти, що перпендикулярність прямих l₁ і  l₂ в просторі означає перпендикулярність прямої l₁  деякій площині  α, якій належить пряма  l₂ ( або l₂β, де l₁Єβ). 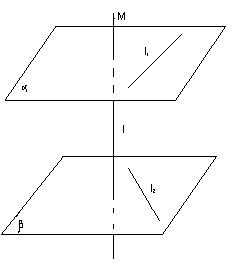Опираючись на це, до задачі можна застосувати такі міркування: шукана пряма l перпендикулярна деякій площині α, проведеній через пряму l₁, і деякій площині β, яка проходить через пряму l₂. Але α l, β l, то α║β.

  рис.2                                                    В ході розв’язування задач учні можуть використовувати і метод доведення деяких теорем. Так, наприклад, аналіз доведення однієї з перших теорем з курсу стереометрії: «Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж тільки одну». І розв’язання  декількох задач, розв’язки яких даються у підручнику, дозволять учням вияснити я. що в курсі стереометрії означають слова «можна провести»,   

«довести, що існує…», сформулювати етапи розв’язування задачі. Доцільно узагальнити план пошуку розв’язку задачі на доведення існування прямих і площин, які задовольняють дані умови. Цей план можна подати так:

а) визначити якою теоремою чи аксіомою можна скористатися для доведення існування прямої чи площини, які будуть задовольняти дані умови;

б) визначити, які і в якій послідовності допоміжні прямі і площини достатньо провести, і яким умовам вони повинні відповідати.

    Основними моментами, які необхідно мати при формуванні умінь розв’язування задач являються:                                                                                                     3

1. вибір задач;
2. використання навчальних взаємодій, які підвищують пізнавальну діяльність учнів, забезпечують можливість переносу умінь.

  Підбираючи систему задач в ході вивчення першого розділу стереометрії, слід  враховувати, що уміння і навики, які учні набули при розв’язуванні задач, являються базою для формування загальнонавчальних умінь і навиків, основними з яких являються уміння виділяти суттєве, планувати, здійснювати самоконтроль у навчанні. Одним з важливих моментів у відборі задач являється врахування їх об’єктивної і суб’єктивної трудності, відповідності розвитку учнів. Рівень об’єктивної  складності задачі суттєво впливає не тільки на діяльність учнів по її  розв’язанню, але і діяльність вчителя по наданню їм необхідної допомоги. А тому слід користуватися такими поняттями:

1. елементарні прості задачі, які розв’язуються 1-2 кроками на основі відомих теорем, аксіом, визначень;
2. елементарні складові задачі – відносно прості по своїй будові, вони являються складовими складних задач;
3. складні задачі першого рівня, які в результаті переформулювання вихідної вимоги порівняно легко зводяться до підзадач елементарних задач;
4. складні задачі другого рівня, процес зведення їх до елементарних задач переважно не викликають труднощів.                                                                    

  Прикладом простої елементарної задачі може бути слідуюча:

Задача 2.Прямі a і b паралельні. Через пряму a проходить площина α.  Яке взаємне розміщення прямої b і площини α?

Дана задача розв’язується на основі теореми:» Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині» і допомагає учням закріпити доведення теореми. Нехай α – площина, b – пряма, яка не лежить у ній,

рис.3                                                              4

a – пряма у площині α, паралельна прямій b. Проведемо площину β через прямі a і b, вона відмінна від α, оскільки пряма b не лежить у площині α. Площини α і β перетинаються по прямій a. Якби пряма b перетинала площину α, то точка перетину   належала б прямій b, але це неможливо, оскільки a і b паралельні. Отже, пряма b паралельна площині α.

      Прикладом простої задачі, в якій можна виділити підзадачі є задача: Через точку однієї з двох паралельних прямих проведена пряма, паралельна другій площині. Доведіть, що пряма лежить у першій площині.

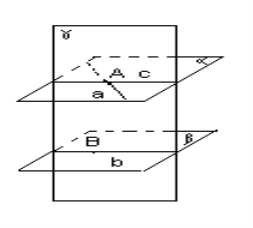     Дана задача відноситься до задач на доведення, зв’язаних із взаємним розміщенням прямих і площин, які відповідають певним умовам. Один із методів розв’язування спирається на використання методу від супротивного, проведення допоміжної площини, яка перетинає дані. Розглядаються лінії перетину даних і допоміжних площин.  Задача зводиться до розв’язування простих підзадач, послідовне розв’язування яких приводить до протиріччя ( в даному випадку з аксіомою паралельних).

рис.4                                               Доведення задачі можна подати. Проведемо площину  γ через пряму a і точку В, взяту на площині  β. Вона перетне площини α і β по прямих с і b   відповідно. Пряма с проходить через точку А і лежить у площині α , тобто має властивості, які потрібно довести. Дальше задача зводиться до доведення того, що пряма с паралельна площині β (задовольняє  решту вимог) і , що прямі а і с співпадають. Обидві задачі є елементарні.

       Після розв’язання декількох задач учні можуть узагальнити план розв’язування задач на доведення, пов’язаних із взаємним розташуванням прямих і площин, які розв’язуються з використанням одночасно методів побудови допоміжних площин і від супротивного.

1. Припущення протилежне даному.
2. Побудова допоміжних площин (одна або декілька).                                    5
3. Довести, що допоміжні площини перетинають дані, звернути увагу на їх лінії перетину.
4. Скласти і розв’язати прості підзадачі, в умови яких входять лінії перетину даних і допоміжних площин і послідовний зв'язок яких може привести до протиріччя або з умовою, або з відомою теоремою чи аксіомою.
5. Зробити висновок про неправильність припущення і правильність твердження сформульованого в умові задачі.

Висновок. Досвід роботи по розв’язуванні задач показує, що виявлення і закріплення в пам’яті учнів тих методів, які використовується в даному розв’язуванні, визначення умов можливості їх використання сприяють формуванню умінь і навичок.

1. Я.Бродський, О.Павлов, А. Сліпенко. Перпендикулярність прямих і площин в курсі стереометрії.  ж. Математика №41 ст.6, №43 ст.6-11, 2005.
2. А.Лемцьо. Методичні зауваження до розв’язування просторових геометричних задач. ж.Математика.                                                    
3. М.Е.Тимощук. О формировании  навыков и умений учащихся при решении  задач первых разделов стереометрии. Математика в школе. №6, ст.39-41, 1983