Стаття "РОЗВИТОК ПІЗНАВАЛЬНОЇ АКТИВНОСТІ НА УРОКАХ МАТЕМАТИКИ"

 

 

 

 

 

 

 

 

 

 

 

 

РОЗВИТОК ПІЗНАВАЛЬНОЇ АКТИВНОСТІ НА УРОКАХ  МАТЕМАТИКИ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ .......................................................................2

ВСТУП ......................................................................3

РОЗДІЛ 1. Психолого-педагогічні основи розвитку пізнавальної активності учнів .....5

1.1 Аналіз психолого-педагогічної та методологічної літератури з проблеми дослідження .....5

1.2 Форми і методи роботи з учнями з метою розвитку пізнавальної активності .....8

РОЗДІЛ 2. Розвиток пізнавальної активності учнів на уроках математики ....14

2.1. Формування творчої активності та мислення на уроках математики .14

2.2. Розробки уроків ....................................................26

ВИСНОВОК ................................................................37

ЛІТЕРАТУРА  ..............................................................39

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Актуальність дослідження

Розвиток пізнавальної активності учнів завжди був ключовою проблемою теорії й практики навчання. Подальший пошук шляхів та засобів залучення учнів до активної пізнавальної діяльності пов̓язаний з соціальними процесами, що відбуваються в суспільстві, з розвитком науково-технічного прогресу, а в зв̓язку з цим із новим ставленням до пошуку інформації та здобування нових знань. Перед сучасною школою постають нові проблеми виховання соціально активної людини, яка може вільно орієнтуватися в потоках різноманітної інформації, вміє вчасно знайти потрібні інформацію та знання, тобто людини, в якій пізнавальна активність є стійкою рисою особистості.

Пізнавальна активність є однією з важливих рис учня, оскільки вона є основою розвитку самостійності, творчої навчально-пізнавальної діяльності, розкриття нахилів і здібностей учнів.

Проблемі розвитку пізнавальної активності школярів присвячені дослідження відомих педагогів, психологів та методистів: Л.П. Арістова, Ю.К. Бабанського, Д.Б.Богоявленської, М.І. Бурди, Д.В. Вількеєва, Л.С. Виготського, П.Я. Гальперіна, Я.І. Грудьонова, В.В. Давадова, М.О. Данилова, В.Є. Єсипова, І.Я. Лернера, М.І. Махмутова, М.І. Шкіля, Г.І. Щукіної, З.І. Слєпкань, Н.А. Менчинської та інші. Серед вітчизняних дисертаційних досліджень останніх років слід відзначити роботи М.Я. Ігнатенка, Л.В. Мар̓яненко, М.С. Голованя, Л.О. Лісіної, в дослідженнях яких детально проаналізовано структуру поняття пізнавальної активності, подано характеристики рівнів та умов, методику розвитку пізнавальної активності учнів на уроках математики в старших класах.

Активний характер навчання є надійною основою розвитку пізнавальної самостійності  школярів. Важливу роль в оволодінні способами пізнавальної діяльності відіграють дії за зразком і аналогією. Водночас спеціальні дослідження і передовий педагогічний досвід показують, що за певних умов навчання учні спроможні успішно виконувати завдання, які вимагають пошуку, розмірковування, самостійних розумових зусиль.

Отже, дослідження проблеми розвитку пізнавальної активності  школярів – важливий резерв інтенсифікації їх навчальної діяльності, необхідна умова наступності навчання і розвитку учнів.

Об'єктом дослідження є навчально-виховний процес, спрямований на активізацію пізнавальної діяльності учнів.

Предмет дослідження - способи активізації пізнавальної діяльності учнів на уроках математики в основній школі.

Мета дослідження - виділити способи активізації пізнавальної діяльності учнів на уроках математики на основі вивчення  основних методів стимулювання розумової активності.

- вивчити основну психолого-педагогічну та методичну літературу з даної проблеми;

- вивчити досвід роботи з питання активізації пізнавальної діяльності учнів на уроках;

- розробити рекомендації з активізації пізнавальної діяльності учнів на уроках математики;

Методи дослідження:

- теоретичний аналіз психолого-педагогічної та методичної літератури з проблеми;

- вивчення досвіду вчителів з питання активізації пізнавальної діяльності учнів на уроках;

- метод створення проблемних ситуацій;

- інтерактивний метод.

РОЗДІЛ 1. Психолого-педагогічні основи розвитку пізнавальної активності учнів

1.1 Аналіз психолого-педагогічної та методологічної літератури з проблеми дослідження

Провідна ідея в педагогічній і методичній практиці — максимально розкрити перед учнем спектр застосування математичних знань, передати своє захоплення предметом вихованцям. Саме в цьому аспекті ми розуміємо один із принципів дидактики в навчанні математики, а саме: принцип свідомості, активності й самостійності.

Цей принцип полягає в цілеспрямованому, активному сприйманні явищ, що вивчаються, їх осмисленні, творчій переробці й застосуванні. Реалізація цього принципу має на меті виконання таких умов:

а) відповідність пізнавальної діяльності учнів закономірностям процесу учіння;

б) пізнавальна активність учнів у процесі учіння;

в) осмислення учнями процесу учіння;

г) оволодіння учнями прийомами розумової діяльності в процесі пізнання нового.

Активність є дієвий стан учня, який характеризується прагненням до учіння, напругою і проявом волі в процесі оволодіння знаннями. Тому активність учнів і називають пізнавальною активністю.

Загальний смисл вимоги активної навчально-пізнавальної діяльності учнів полягає в тому, що ця вимога має два аспекти: внутрішній (психолого-педагогічний) і зовнішній (організаційний).

Внутрішній аспект активної навчальної діяльності школярів полягає в тому, що вона визначається такими компонентами, як інтерес до навчання, ініціативність у навчальній роботі, пізнавальна самостійність, напруження фізичних і розумових сил для розв'язання поставленої пізнавальної задачі. Розвиток цих компонентів і складає необхідну умову організації активної навчально-пізнавальної діяльності учнів.

Зовнішній аспект активної навчальної діяльності школярів полягає в тому, що до цієї діяльності необхідно залучити всіх учнів даного класу і кожного з них.

Основною методологічною концепцією педагогічної психології є положення про те, що особистість формується лише в процесі активної діяльності. Формування особистості можна і слід відповідно спрямувати. Важливим засобом є керування дорослих діяльністю дітей або - в широкому розумінні - організація всього їхнього життя й активного спілкування.

Вчені стверджують, що з погляду активізації пізнавальної діяльності, розумових здібностей і підвищення якості знань найкращим способом є цілком самостійне добування знань на основі пошуку і дослідження. Хоч в пізнанні не можна обійтись без репродуктивної діяльності.

Найбільш яскраво питання самостійного мислення, творчості і активності розроблялись в епоху Відродження педагогами-гуманістами Еразмом Роттердамським, Вітторіно да Фельтре, Франсуа Рабле, Томасом Мором. Пізніше - Ян Амос Коменський у «Великій дидактиці» писав: «Яке б заняття не починати, перш за все треба викликати в учнів любов до нього, довести особливість цього предмета, його користь, приємність і що тільки можливо Великий вчений пов'язував рішення цієї проблеми з процесом навчання і виховання, особистістю вчителя, його підготовкою, якістю підручника, умінням ним користуватись. Я.А. Коменський впритул підійшов до ідеї формування в учнів творчого мислення, завдяки якому учень був би здатний до самостійного відкриття, творчості.

Ряд педагогів і психологів розробляли проблему рівнів розвитку інтересу до навчання. Так, Г.І. Щукіна вважає, що за основу слід взяти активність і самостійність учнів, бажання перебороти будь-які труднощі (високий рівень - висока активність, самостійна робота протікає із захопленням, бажання перебороти труднощі у складних завданнях; середній рівень - пізнавальна активність викликається за допомогою стимулювання вчителя, ситуативне виконання самостійної роботи, труднощі долає з допомогою вчителя; низький рівень - пізнавальна інертність, мінімальна самостійність, бездіяльність при затрудненнях.

Повноцінна навчально-пізнавальна діяльність містить три складові: орієнтувальну, виконавчу, контрольну. Контроль відіграє важливе навчальне, розвивальне і виховне значення. Він дозволяє виявити повноту, глибину, свідомість і міцність знань на різних етапах навчання, сприяє корекції, управлінню і самоуправлінню процесом навчання, спонукає учнів до активної розумової діяльності, сприяє виробленню свідомого їх ставлення до систематичної навчальної праці. Це залежить як від індивідуальних особливостей учнів, так і від об'єктивно існуючих умов (змісту навчального матеріалу, логіки предмета математики, закономірностей навчального процесу, гносеологічних основ учіння тощо).

Рушійною силою процесу пізнання є внутрішні суперечності між завданнями, які ускладнюються, і вимогами до навчання та наявними можливостями учня. Розвиток процесу навчання математики є поступовим, еволюційним, у ньому неперервно поєднуються протилежні процеси: суто логічні міркування: уява, інтуїція, чуттєво-наочне, конкретне і абстрактне, індуктивні і дедуктивні матеріали, змістовні і формалізовані.  Найбільш поширеною суперечністю навчально-пізнавальної діяльності є суперечність між особистим досвідом школяра і елементами наукових знань з математики, які він набуває в школі.

Необхідною умовою активізації навчально-пізнавальної діяльності учнів є систематичне і цілеспрямоване виховання їх в процесі навчання математики прийомами розумової і навчальної діяльності. Ці прийоми різноманітні як за змістом, так і за функціями та джерелами їх оволодіння. Одні повідомляє вчитель, а учні опановують і використовують у процесі навчання - інші учні знаходять і опановують самостійно, застосовують при виконанні певних навчальних завдань.

Нарешті, принцип індивідуалізації і диференціації як один з провідних принципів розвивального навчання, створює сприятливі умови для активізації знань школярів. У вирішенні проблеми дослідження важливим чинником є взаємозв'язок різних видів навчальної діяльності для її активізації, що допомагає розкриттю потеніційних можливостей кожного учня.

Отже, аналіз психолого-педагогічної та методологічної літератури свідчить, що багато вітчизняних і зарубіжних педагогів займалися проблемою активізації навчально-пізнавальної активності дітей на уроці. Дослідження практиків показали, що потрібно ураховувати чинники, що гальмують розвиток навчально-пізнавальної діяльності учнів. Запобігати перевантаженню розумових сил або тривалої одноманітності навчальної праці, необ’єктивного зниження оцінки під час виконання ними завдань.

1.2 Форми і методи роботи з учнями з метою розвитку пізнавальної активності

В навчальному процесі у школі застосовуються різноманітні методи, технології та педагогічні прийоми стимулювання пізнавальної діяльності учнів. Зокрема, традиційні та інноваційні, пасивні, активні та інтерактивні методи. До традиційних форм навчальної роботи належать пасивні та активні методи.

У навчальному процесі активність учнів проявляється не лише в роботі думки, а й у практичній діяльності, в позакласній — позаурочній роботі, в напруженні волі, а також в емоційних переживаннях.

Розумова активність учнів у процесі навчання математики має особливе значення в формуванні понять, осмисленні їх, практичному застосуванні й, особливо, в умінні самостійно оперувати цими поняттями. Тому доцільно розглянути методи й форми роботи для реалізації цілей. В першу чергу це:

1. Груповий метод під час розв'язування задач. Робота в парах.

2. Різні форми роботи з книгою.

3. Застосування різних видів заохочень.

4. Самостійні роботи із застосуванням аналогій, порівнянь, карток-інструкцій і консультацій.

5. Використання на уроках елементів історизму, зацікавленості (уроки-казки, уроки-подорожі, уроки-кросворди і т.д.).

6. Використання проблемних ситуацій.

7. Виклад матеріалу блоками.

8. Наочність, доступність, оригінальність розв'язань різними способами, самостійність в одержанні знань, вибір методу розв'язування задачі, зв'язок науки з практикою, анкетування, тестування.

9.Спостереження за мовою, рецензування за схемою .

Шляхи і методи активізації пізнавальної діяльності можуть бути здійснені тільки з допомогою умілого поєднання фронтальної, групової, індивідуальної роботи учнів, а також за допомогою сучасних засобів індивідуального навчання. Такими засобами є дидактичні матеріали з друкованою основою, карточки-інструкції, карточки-зразки, засоби програмованого контролю і т.д.

Завдання вчителя полягає в тому, щоб поряд з вивченням понятійного апарату даної теорії постійно демонструвались прийоми і способи пізнавальної діяльності.

За своєю формою прийоми і способи діяльності описуються:

а) алгоритмічними приписами, алгоритмічними схемами, блок-схемами;

б) правилами і законами логіки.

В процесі своєї діяльності учень користується готовими алгоритмічними приписами, правилами і законами або самостійно їх складає. У першому випадку ним здійснюється репродуктивна, а у другому - продуктивна діяльність.

Однією з форм, що активно запроваджується вчителями математики в навчальний процес, є нетрадиційні уроки. Так називають уроки, що не вкладаються в рамки традиційної методики навчання, на яких учитель дотримується стандартної структури, методів і прийомів навчання. Нетрадиційний урок — це передусім творчість, самобутність і навіть мистецтво вчителя. Такий урок може максимально стимулювати пізнавальну самостійність, творчу активність та ініціативу учнів, їх інтерес до навчання.

Розрізняють такі види нетрадиційних уроків: інтегровані, міжпредметні, театралізовані, ігрові, з різновіковим складом учнів та ін. Загалом, за формою організації нетрадиційні уроки бувають такі: урок-лекція, урок-практикум, урок-семінар, урок-залік, урок-КВК, урок-подорож, урок-гра «Математичний бій», урок-гра «Брейн-ринг», урок-аукціон, біт-урок, урок-вікторина, бінарний урок, тощо. Технологія та конкрекретні розробки нетрадиційних уроків мають важливе значення.

І сьогодні освіта не може бути вдосконалена без принципового переосмислення ролі вчителя у навчально-виховному процесі. Учитель нині повинен навчатися управляти діяльністю як усього колективу учнів, так і кожного окремого учня, проте це неможливо в межах традиційного уявлення про педагогічний процес. Кращі вчителі завжди ведуть пошук, використовують активні методи навчання: роботу в малих групах бригадах, парах. Кожний учитель бере на озброєння все найкраще. Використовують технічні засоби навчання, вводять опорні сигнали, роботу асистентів, збільшують час самостійної роботи на уроці

Постійно застосовувати аналітико-синтетичний метод – як під час пошуку розв'язку задачі, так і під час виведення правила чи доведення теореми, а також в якості організаційної форми застосовувати колективну пояснювальну бесіду, охоплюючи при цьому якнайбільшу частину учнів класу.

Як один з прийомів активізації самостійної діяльності учнів можна проводити підготовлених окремими учнями п'яти – семи хвилинних повідомлень з питань, які безпосередньо відносяться до програмового матеріалу. Сюди ж відносяться і більш складні задачі. До цього намагатися залучати якнайбільше різних учнів класу; матеріал для їх виступу підбирати з урахуванням їх підготовки з математики, розвитку мови і т.д.

Поняття готовності до пошукової діяльності характеризує вміння учнів розв’язувати конкретну розумову чи практичну задачу, виконувати завдання на окремих етапах її розв’язування, а також визначає загальну готовність до пошуку, яка є найважливішою саме а початковому навчанні. Під загальною готовністю до пошукової діяльності слід розуміти інтегральний стан особистості, який включає окремі підструктури (мотиваційну, змістову, організаційно-процесуальну), що функціонують в цілісній системі.

Загальна готовністьучнів до пошукової діяльності включає 3 компоненти:

1.Мотиваційний компонент

Він має на меті пробудити і закріпити в дітей позитивні емоції у процесі колективної навчальної діяльності, викликати інтерес, допитливість, бажання до самостійного розмірковування і як наслідок – сформувати прагнення до пошукової діяльності.

Формування мотиваційного компонента повинно створювати в навчанні особливий емоційний мікроклімат, який стимулює інтелектуальні почуття дітей: здивування, зацікавленість, захоплення, інтерес, задоволення від усвідомлення переборення труднощів Водночас, турбуючись про відповідний емоційний фон навчання, важливо пам’ятати про доцільне співвідношення логічних і емоційних елементів у пошуковій діяльності. Пошукова діяльність обов’язково передбачає контроль і оцінку результатів. Контрольно-оцінний елемент у пошуковій діяльності молодших школярів відіграє спонукальну роль. Швидка й об’єктивна оцінка вчителем в розв’язуванні проблемних і пізнавальних задач багато в чому визначає інтелектуальну активність учня, прагнення досягти результату.

Створенню необхідного мотиваційного настрою учнів сприяє вміле використання ігрових ситуацій.

Мотиваційний компонент дуже тісно пов’язаний із змістом і характером пошукової діяльності.

2.Змістовий компонент

Успішне розв’язання  школярами проблемних і пізнавальних завдань можливе, якщо вони володіють міцними знаннями, які вміють комбінувати в процесі пошуку. Готовність до розв’язування проблемних і пізнавальних завдань вимагає і спеціального запровадження в навчальний процес розвиваючих завдань, активізуючи запитань, педагогічно доцільного поєднання репродуктивних і творчих завдань.

Найбільшу роль у змістовому компоненті відіграє система пізнавальних завдань, яка мала випереджаючий характер порівняно з досягнутим рівнем розвитку учнів.

3. Організаційно-процесуальний компонент

Готовність до пошукової діяльності передбачає здатність учнів до швидкого відбору потрібної інформації, уміння виділити головне, поставити запитання, пов’язати відоме з невідомим.

Які ж дидактичні умови розвитку пізнавальної самостійності?

 Для успішного формування усіх компонентів готовності школярів до пошукової діяльності в організації навчально-виховного процесу потрібно:

1. Формувати в учнів пізнавальні потреби, сприяти розвитку наполегливості у виконанні самостійних завдань.

2. Добиватися раціонального поєднання репродуктивної і продуктивної діяльності учнів, доцільно збільшувати питому вагу частково-пошукових методів, які сприяють активному, перетворюючому характеру засвоєння знань і способів їх переробки.

3. Запровадити в зміст навчання спеціальну систему пізнавальних завдань, яка оптимально забезпечує пізнавальну, розвиваючу й виховну функції навчання.

4. Використовувати ефективні засоби керування пошуковою діяльністю школярів через поступове ускладнення і варіювання змісту пізнавальних завдань, а також в результаті операційного формування пошукових умінь.

5. Озброювати  учнів системою інтелектуальних умінь, загальних та спеціальних прийомів навчальної роботи.

У сучасній дидактиці вважається, що пізнавальна самостійність виявляється у потребі й умінні учня самостійно мислити, у здатності орієнтуватися в новій ситуації, самому бачити питання, задачу і знайти підхід до її розв’язання.

Отже, найважливішою умовою активізації навчально-пізнавальної діяльності є забезпечення мотивації навчання, яка підвищує інтерес учнів до знань, викликає наполегливість, сприяє засвоєнню нових знань, прагненню досягти поставленої мети.

 

РОЗДІЛ 2. Розвиток пізнавальної активності учнів на уроках математики

2.1. Формування творчої активності та мислення на уроках математики

Сучасна педагогіка і психологія спрямовує свої зусилля на те, щоб виявити здібності учня, максимально використати їх для розвитку його особистості. Цього можна досягнути не лише вдосконаленням змісту шкільного курсу будь-якої дисципліни, а й впровадженням таких методів, засобів та організаційних форм навчання, які б активізували пізнавальну діяльність учнів, розвивали їх мислення, здібності, привчали працювати самостійно і творчо.

Планування своєї діяльності

Особливу увагу слід звертати на завдання, які формують вміння аналізувати, порівнювати, узагальнювати, виділяти головне, контролювати і планувати свою діяльність. Так, при проходженні теми “Рішення трикутників”, учням можна запропонувати домашнє завдання: скласти розповідь про теореми синусів і косинусів за планом:

1.                       Що ви знаєте про виникнення теореми
2.                       Якого типу завдання ви можете вирішувати за допомогою цих теорем
3.                       Як можна використовувати ці теореми в інших предметах або в практичному житті людини.

Такі завдання систематизують знання учнів, вчать їх бачити основне, підвищують мовну активність.

Різні підходи до вирішення однієї і тієї ж задачі

Для виховання пізнавальної активності школярів можна використовувати у своїй практиці ознайомлення їх з різними способами доведення теорем, різними підходами до вирішення однієї і тієї ж задачі.

Завдання: В одній цистерні 59 т нафти, в іншій – 44 т. Через скільки днів в цистернах залишиться однакову кількість пального, якщо щодня з першої витрачається 5 т, а з другої 2 т.

Рішення: I спосіб – алгебраїчний.

59-5х = 44-2х, х = 5 (днів).

II спосіб – арифметичний.

1. 59-44 = 15, 2) 5-2 = 3, 3) 15: 3 = 5 (днів).

Ігри

1.                       Гра в якій учитель називає поспіль числа, а учні числа, які кратні трьом, повинні, правильна відповідь супроводжується оплеском . Ряд, який менше допускав помилок, є переможцем.
2.                       “Рахунок-додаток”. Учитель записує на дошці якесь число, припустимо, 15,7. Потім він повільно називає число, яке менше, ніж 15,7. Учні повинні у відповідь назвати інше число, яке доповнює дане до 15,7. Ті числа, які називає учитель, і ті, що дають учні, не записуються. Цим забезпечується тренування в запам’ятовуванні чисел.
3.                       “Поспішай, та не помилися”. Ця гра – фактично математичний диктант. Учитель повільно прочитує завдання за завданням, а учні на листах записують відповіді.
4.                       “Не зівай”. Учні кожного ряду отримують по картці. У першого учня в ряду завдання написано повністю, а у всіх інших замість першого числа написано три крапки. Що ховається за трьома крапками, учень дізнається тільки тоді, коли його товариш, що сидить попереду, повідомить йому відповідь у своєму завданні. Ця відповідь і буде відсутньою числом. У такій грі всі повинні бути уважні, оскільки помилка одного учня закреслює роботу всіх інших.
5.                       “Склади слово”. Учитель пропонує на картці написані зверху вниз 5-6 прикладів, і на кожен приклад 3-4 варіанти відповіді, які закодовані буквами. Учні в класі розбиваються на кілька команд, зазвичай команду складають сидячи один за одним. Кожен з членів команди вирішує відповідний приклад, вибирає правильну відповідь і записує букву-код. Після закінчення рахунку у учнів з’являється слово (бажано похвала).
6.                       “Математична естафета”. У V-VI класах увага учнів нестійка. Виникає необхідність на уроці перемикатися з одного виду діяльності на інший. У цьому випадку виручає математична естафета. Кращий результат дають естафети, що проводяться в кінці уроку.

Наприклад, при вивченні теми: “Множення одночленів”, можна провести естафету. На кожен ряд роздають по однаковою картці, що грає роль естафетної палички, на якій зображені множники, наступні множники і остаточний результат – добуток. Учням дається завдання “закрити кватирки”, тобто заповнити порожні місця проміжними добутками, які записують тільки простим олівцем і після того, як ретельно перевірено рішення попередніх прикладів. Ця естафета розвиває також вміння контролювати себе.

Завдання з практичним змістом

Одним із засобів активізації пізнавальної діяльності школярів є широке використання їх життєвого досвіду. Велику роль при цьому відіграють практичні роботи, а також вирішення завдань з практичним змістом.

Так, пояснення теми “Координатна площина” в 6-му класі можна почати з питання: “Вкажіть зі своєї життєвої практики приклади, де положення об’єкта задається за допомогою чисел”. Учні по черзі називають приклади: місце в кінозалі, положення фігури на шахівниці, широта і довгота місця на карті і ін. Потім формулюється завдання …

Вивчення питання про суму n-перше членах арифметичної прогресії в 9-му класі можна почати з розповіді: “Приблизно 200 років тому в одній зі шкіл Німеччини на уроці математики вчитель запропонував учням знайти суму перших 100 натуральних чисел. Всі почали поспіль складати числа, а один учень майже відразу ж дав правильну відповідь. Ім’я цього учня Карл Фрідріх Гаус. Надалі він став великим математиком. Як вдалося Гауса так швидко підрахувати цю суму? ”

Учням пропонується пошукати рішення цього завдання, подумати, як простіше і зручніше виконати його. Поступово учні знаходять правильне рішення: (1 + 100) * 50 = 5050. Потім з’ясовуємо, що послідовність 1,2,3, …, 100 є окремий випадок арифметичної прогресії і виводимо формулу для суми n-перших членів.

У процесі пояснення нового матеріалу важливо так спрямувати роботу дітей, щоб вони доходили висновків на основі цільового порівняння та порівняння нових знань з тими, що здобуті раніше, засвоювали б узагальнення силою власного мислення, активізованого вчителем. Для цього необхідно правильно організувати дидактичний матеріал, щоб учні усвідомили недостатність раніше засвоєних знань і були психологічно готові до засвоєння нових.

У процесі вивчення розподільної властивості добутку порівняння наведених записів створює проблемну ситуацію.

(53+47)∙2=100∙2=200

(53+47)∙2=53∙2+47∙2=200

-Що спільне в цих прикладах? (Однакові співмножники і добутки).

-Чим вони відрізняються? (У першому прикладі знайшли суму і помножили на 2, а у другому – кожний доданок множили на 2, а результати додали).

-Чи змінився результат дії? (Ні, результати однакові).

-Чому? Який можна зробити висновок? (Щоб помножити число на суму, можна спочатку знайти суму і на цей результат помножити число або число помножити на кожний з доданків, а знайдені добутки скласти. Результат дії від цього не зміниться).

У дев‘ятому класі, під час вивчення теми “Відсоткові розрахунки” вчитель може створити проблемну ситуацію, яка збуджує емоції учнів та зацікавлює в пошуку відповіді на таку життєво важливу задачу: “Яка загальна формула нарахування відсоткових грошей в банку, якщо в банк покласти S₀ гривень під р % на n років, а відсотки нараховуються один раз на рік?” Пошук відповіді на це завдання проводить до виведення формул простого та складного відсотку за допомогою послідовних відповідей на такі запитання:

1.         Яка сума нараховується на вклад через 1 рік?

2.         Яка сума з‘являється на вкладі через 1 рік?

3.         Які відсоткові гроші нараховуються на 2-ий рік?

4.         Яким стане вклад через два роки з врахуванням початкової суми вкладу?

Далі, проводячи аналогічні міркування про третій та четвертий роки, учні помічають закономірність між зміною суми вкладу, кількістю років та відсотковою ставкою банку. В результаті, виводяться формули:

 - формула складного відсотку, (2.1)

 - формула простого відсотку, (2.2)

де S_n – сума вкладу після n нарахувань,

S₀ – початкова сума вкладу,

p – відсоткова ставка банку,

n – кількість нарахувань

Для сильних учнів, які знайомі з методом математичної індукції, можна запропонувати довести одержані формули відповідним методом.

Обов̓язково потрібно провести порівняльний аналіз цих формул та звернути увагу учнів на те, що відсотки називають простими, якщо нарахування відбуваються постійно на початковий капітал, а складні відсотки нараховуються на капітал, який утворюється протягом певного періоду.

Особливість нарахувань відсотків щомісячно можна проілюструвати на прикладі:

Задача . Обчислити відсоткові гроші у випадку вкладу 1000 грн. під  12 % річних, якщо відсотки нараховуються кожного місяця.

Перед розв’язанням задачі учні колективно шукають відповідь на запитання: Як знайти відсоткову ставку щомісячних нарахувань, якщо відома річна відсоткова ставка?

Для закріплення цього факту учням пропонується за даними задачі відповісти на запитання, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Після цього можна запропонувати самостійну роботу на виведення формули нарахувань відсоткових грошей, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Робиться висновок, що під n у формулі розуміється кількість періодів нарахування відсотків.

Для порівняння дії цих формул корисно запропонувати учням самостійно знайти складний відсоток, щоб через три роки на вкладі була така ж сама сума грошей, як і при простому відсотку нарахувань. Таке завдання активізує учнів та вчить порівнювати результати нарахування відсоткових грошей, аналізувати математичні данні.

Вивчення передового педагогічного досвіду показує, що велику розумову активність викликає розв’язування таких завдань, які вимагають від учнів логічного розмірковування, комбінування, співвіднесення даних умови і відповідей. Такі завдання дуже корисні, це ніби розумова гімнастика.

Наприклад, на уроках математики в 6  класі можна використовувати такі завдання:

 

1.Є  три числа: -3; 5; -7. Додали два  числа і від цієї суми відняли третє число. Вийшло деяке від’ємне число. Яке?

 2.

4	0	-9	2
-3	5	-8	-4
3	-7	12	-6
-11	-1	-5	11

 Сума чотирьох чисел, що стоять в одному ряді (по вертикалі, або по горизонталі, або по діагоналі), дорівнює: а) -10; б) -24. назвіть ці числа.

3. Знайти суму всіх цілих чисел від -599 до 601.

Також для активізації навчальної діяльності учнів добре використовувати такі методи , як «Мікрофон», «Асоціативний кущ», «Мозковий штурм».

Наприклад, при вивченні теми «Задачі на рух по річці» вчитель пропонує учням роз’язати задачу: Два теплоходи рухаються по річці назустріч один одному. Перший теплохід має власну швидкість 26км/год, другий 30км/год. Зараз між ними відстань 100км. Якою буде відстань через 0.5год?

  Обговорення розвязання задачі виконується з використанням методу “Мікрофон”. Учні, які мають припущення щодо розвязання задачі, говорять у “мікрофон”. Висловлювання одних наштовхують на нові думки інших.

   Мета обговорення розв'язання цієї задачі полягає в тому, що учні повинні зробити висновок: задачу розв'язати неможливо, бо не всі дані відомі

Подобається дітям, коли вчитель дає завдання на виправлення навмисно зроблених помилок в рішенні.

Приклади створення проблемних ситуацій.

Приклад 1

На дошці швидко записується розв’язання рівняння. При цьому умисно робиться помилка:

(3х+7)*2-3=17,

6х+14-3=17,

6х=0,

х=0.

Звичайно, при перевірці відповідь не співпадає. Діти шукають помилку, таким чином розв’язують проблему. Результат – уважність і зацікавленість учнів на уроці.

Приклад 2

Під час розв’язування квадратного рівняння, допускається навмисна помилка

3² - 2х-2=0,

D= 2^2-4*3*(-2) =25.

Після знаходження коренів учням пропонується зробити перевірку. Вона показує, що знайдені числа не є коренями даного рівняння. Знаходять помилку  D=28.

Такі приклади активізують діяльність учнів.

У програмі з математики зазначено, що математика, давно ставши мовою науки і техніки, в даний час все ширше проникає в повсякденне життя і повсякденний мову, все більше впроваджується в традиційно далекі від неї області. Тому є важливим питання здійснення міжпредметних зв’язків, що сприяє підвищенню пізнавального інтересу.

Слід показати, що знання математики необхідні у всіх областях, а також знання інших предметів можна використовувати в математиці.

Наприклад:

1.«На земній кулі літають птахи – безпомилкові укладачі прогнозу погоди на літо. Якщо ви правильно вирішите приклади, записані на дошці, то ви дізнаєтеся одну з них ». Замініть приватні буквами, і ви дізнаєтеся такого птаха. (Фламінго з піску будують гнізда у формі усіченого конуса, в верхньому підставі роблять поглиблення, в які відкладають яйця. Висота гнізда залежить від того, яким буде літо: сухим або дощовим. Якщо літо очікується дощовим, то гнізда будуються високими, щоб їх не могла затопити вода, якщо посушливе, то нижчими).

2. Вирішивши приклад, ви отримаєте масу черепахи-гіганта, що живе на островах Тихого океану. Вона такої величини, що діти можуть кататися, сидячи на її панцирі.

(Найбільша в світі черепаха важить 600 кг. Вона називається дермохеліс. З її панцира виготовляють прикраси, а м’ясо і яйця йдуть в їжу).

3.              Вирішуючи приклади і розташовуючи відповіді прикладів у порядку зростання, ви отримаєте назву міста, єдиного в своєму роді, іншого такого немає на світі. Воно стоїть в морі, на 118 островах, розташованих в 4 км від суші. У цьому місті немає автобусів, тролейбусів, а засобом пересування є річкові трамваї – катери і гондоли (Венеція).

Використання під час уроків інформації з інших предметів дозволяє здійснювати міжпредметні зв’язки, виховувати в учнях допитливість, прагнення пізнати нове, розширити їх кругозір. Тому подібні фрагменти можна включати до  уроків.

У 6 класі починається курс географії, і можна застосувати знання учнів з цієї науки на своїх уроках в темах: «Масштаб», «Графіки». Так, при вивченні теми «Масштаб» можна працювати по географічній карті , виконуючи практичну роботу: «Визначити відстань від Харківа до Київа на місцевості, вимірявши його на карті». Інтерес учнів на таких уроках високий.

Отже, засобів активізації в арсеналі вчителя чимало, і треба їх широко й уміло застосовувати, враховуючи при цьому мету уроку, характер матеріалу, рівень підготовки учнів і власні можливості.

 

 

Підвищення ефективності самостійної роботи

Самостійною на уроці вважається така робота, яку учні виконують без участі вчителя, а лише за його завданням у спеціально визначений час. При цьому вони свідомо прагнуть досягти поставленої мети, виявляючи свої зусилля в тих чи інших діях.

 

Самостійність учнів у навчанні є найважливішою передумовою свідомого і міцного оволодіння знаннями. Часто застосовувана самостійна робота розвиває зосередженість, цілеспрямованість, уміння міркувати, запобігає формалізму в засвоєнні знань і взагалі формує самостійність як особливість мислення і рису характеру дитини.

 Останнім часом на уроках математики, крім підручника, дедалі частіше використовують друковані картки. Використання карток під час підготовки до вивчення нової теми зосереджує увагу учнів на потрібному правилі чи способі перевірки, а вчителеві допомагає своєчасно виявити прогалини в знаннях окремих учнів, застосовувати диференційовані завдання. Виконуючи індивідуальну роботу з картками, «слабкі» учні можуть працювати з картками-підказками,  «сильні» виконувати завдання більш високого рівня складності. Наприклад, при вивченні теми «Додавання раціональних чисел», учням можна запропонувати слідуючі картки:

Картки-підказки для «слабких» учнів

При додаванні двох чисел з різними знаками, треба: Знайти модулі чисел, які додаються; 2) від бідьшого модуля відняти менший модуль; 3) перед здобутою різницею поставити знак того числа, в якого модуль більший. Наприклад: -20+(+150=-(│-20│-│+15│)=-(20-15)=-15 │-20│>│+15│ Так само виконайте додавання чисел, заповнивши пропуски. а) -30+17=…(│…│-│…│)=…(…-…)=…│-30│…│+17│ б) -27+43=…(│…│-│…│)=…(…-…)=…│-27│…│43│ в) -3,5+2,7==…(│…│-│…│)=…(…-…)=…│-3,5│…│2,7│

 

Картки для « сильних» учнів

Знайдіть значення а+б при даних значеннях а та б   а 5,14 -6 5,71 -2 -(-2) -5,033 б -3 7 -5,71 -6 2 7

 

Дуже вдалою є форма таких карток, яка дає змогу виконувати завдання безпосередньо на картці.

Крім розв’язування прикладів і задач, учні 5-6-х класів можуть самостійно виконувати різноманітні завдання, спрямовані на опанування геометричного матеріалу. Це, зокрема, знаходження довжини ламаної лінії; впізнавання геометричних фігур (на плакаті, картах), побудова заданих фігур (трикутників, чотирикутників, ламаної лінії, кола); обчислення площі трикутника, обчислення і порівняння периметрів фігур.

В організації самостійної роботи учнів важливу роль відіграють задачі за готовими малюнками. Розв’язування таких задач дозволяє економити час, сприяє розвитку математичної мови учнів, формує навички застосування співвідношень між елементами.

Задачі за готовими малюнками на обчислення та на доведення можна використовувати для самостійних та контрольних робіт. Накресливши на дошці один малюнок, пропонуються до нього кілька задач з різними даними.

Різноманітність варіантів гарантує самостійність роботи учнів.

Для тренувальної самостійної роботи учням корисно давати посильні завдання, які не потребують виконання великої механічної роботи, але вимагають напруження думки. Наприклад, на уроках математики в 6 класі для індивідуальної роботи можна використати такі завдання:

1.Серед виразів знайдіть рівні:

 

a-b-(-с)

a+b+c

a+(-b)+(-c)

a+(-b)+c

a-(-b)-(-c)

2. Замість квадратиків запишіть такі числа, щоб утворились правильні рівності:

а) -9-12=9-□

б) -2+□=□-3

в) □-7=13-□

г) □+□= -8

д) □-□= -8

3. Замініть зірочки знаками «+» або «-» так, щоб утворились правильні рівності:

7,2*(-5,3)=12,5

3,6*8,1= -4,5

-6,1*(-2,3)*3,8=0

-3,7*(-6,9)= -10,1

-4,9*1,7= -3,2

Отже, щоб навчити учнів активно і свідомо працювати, слід широко використовувати різноманітні за змістом і характером самостійні завдання на всіх етапах опрацювання матеріалу: у підготовчих вправах, під час засвоєння нових знань і способів дій, у процесі закріплення і формування вмінь і навичок.

 

2.2. Розробки уроків

 

Тема: Трикутник. Види трикутників. Периметр трикутника

Мета уроку:

• навчальна: подальше закріплення знань учнями класифікації трикутників; сформувати вміння будувати трикутники за двома сторонами і кутом між ними та за стороною і прилеглими кутами;
• розвиваюча мета: розвивати пізнавальну діяльність, мовний розвиток (називати приклади, пояснювати хід практичних дій).
• виховна: виховувати охайність пі час виконання геометричних побудов;

Тип уроку: комбінований

Обладнання:транспортир, лінійка, косинець.

 

План уроку

 

1. Домашнє Організаційний етап
2. Перевірка домашнього завдання
3. Актуалізація опорних знань
4. Вивчення нового матеріалу
5. Закріплення матеріалу
6. Підсумок уроку завдання

 

Хід уроку

 

І. Організаційний етап

 Перевірка готовності учнів до уроку.

 Формування мети та задач уроку.

ІІ. Перевірка домашнього завдання

Перевірка №351

IIІ. Актуалізація опорних знань

1. Вправа «Знайди трикутник»

Слова учителя:

Про що ви дізналися на попередньому уроці?

Відповіді:  які існують види трикутників; як знайти периметр трикутника.

Знайти на дошці і показати трикутники, що відповідають заданому виду:

 Прямокутний різносторонній

 Гострокутний різносторонній

 Тупокутний різносторонній

 Рівнобедрений тупокутний

 Рівносторонній

 Рівнобедрений гострокутний

 Рівнобедрений прямокутний

2.  Знайдіть периметр

Усно розв’язати задачу, за умовою поданою на дошці

 

 

 

 

 

 

 

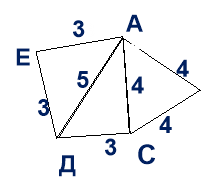
* Рівностороннього трикутника;

* Рівнобедреного трикутника;

* Різностороннього трикутника

IV. Вивчення нового матеріалу

1. Приклад побудови трикутника за двома сторонами і кутом між ними.

Ст. 109, приклад 1

2. Приклад побудови трикутника за стороною і прилеглими кутами.

Ст. 110, приклад 2.

Після цього, проаналізувавши побудову, доходимо висновку, що:

за двома сторонами і кутом між ними побудову трикутника викону­ють у такому порядку: будуємо кут; на його сторонах відкладаємо 2 відрізки відомої довжини;

За стороною і двома прилеглими до неї кутами побудову трикутника ви­конують у такому порядку: будуємо сторону; від неї відкладаємо 2 кути.

V. Закріплення матеріалу

Робота за підручником (п.14)

№354

VІ. Підсумок уроку

1. Що ми знаємо про трикутники: 

Перед вами зображений рівнобедрений трикутник АВС

Назвіть:

а) основу;

б) бічні сторони;

в) кути при основі;

г) кут, протилежний основі

 

2. Визначте вид трикутника

за його кутами:

а) 34 ; 127 ; 19 ;

б) 40 ;  50  ;  90  ;

в) 45 ; 60  ;  75  ;

г) 95  ; 80  ;  5 ;

 

3. Розв'яжіть задачу:

Дріт завдовжки 15 см зігнули так, що отримали рівносторонній трикутник. Який периметр цього трикутника? Яка довжина сторони? 

4. Розв'яжіть задачу:

 

Взяли дріт завдовжки 19 см і з нього зробили трикутник, дві сторони якого дорівнюють 5 см і 7 см. Що ви можете сказати про цей трикутник?

VІІ. Домашнє завдання

П. 14, № 355

№ 358

 

 

 

Тема: Множення. Переставна властивість множення.

Мета: узагальнити і систематизувати знання учнів про зміст дії множення натуральних чисел, про переставну властивість множення; властивості нуля і одиниці під час множення;формувати навички множення багатоцифрових чисел; розвивати  пам’ять, увагу, мислення; виховувати наполегливість, старанність, акуратність  під час виконання записів у зошитах.

Обладнання: таблиці, картки.

Тип уроку: узагальнення і систематизації знань.

 

 

Хід уроку

І. Організація учнів до уроку.

                                                  

ІІ. Актуалізація опорних знань учнів. Повідомлення теми, мети уроку.

1. Розгадування кросворду.

Вчитель:

- Щоб дізнатися над якою темою ми будемо сьогодні працювати, розгадайте кросворд (Додаток 1)

Завдання до кросворду:

1. Сума довжин усіх сторін многокутника ( периметр).

2. П’ять відняти п’ять ( нуль).

3. Чотирикутник, у якого всі кути прямі ( прямокутник)

4. Кожен відрізок має певну...( довжину)

5. Добуток чисел 15 і 4 ( шістдесят)

6. Один помножити на один (один)

7. Сімнадцять помножити на  один ( сімнадцять).

8. Збільшіть 25 у 2 рази( п’ятдесят)

 

2. Бесіда. Запис теми з зошити.

- Яке ж слово зашифроване по вертикалі ( Множення).

- Які властивості множення вам відомі? ( Переставна, сполучна, розподільна).

- Сьогодні на уроці ми працюємо над темою „Множення. Переставна властивість множення”. Тому в зошити так записуємо

( Вчитель звертає увагу на запис на дошці, зроблений перед початком уроку для зразка)

- Якщо ви звернули увагу, то ми вже множили, коли розгадували кросворд, а значить ця тема не є для вас новою. Тож сьогодні ми тільки узагальнюємо та систематизовуємо ваші знання про зміст дії множення натуральних чисел, про переставну властивість множення, повторимо, що є добутком  будь – якого числа і одиниці та  нуля і будь – якого числа, удосконалюватимемо навички множення багатоцифрових чисел. Тож починаємо роботу.

 

ІІІ. Повторення, систематизація та закріплення знань учнів.

1.               Робота за рисунком  ( на дошці). Пояснення з елементами бесіди.

Бесіда:

•                   Скільки квадратів зображено на рисунку? ( 15)
•                   Як ви про це дізнались ( порахували)

 Легко збагнути, що шукане число квадратів дорівнює 5 + 5+5=15. Пригадайте, як можна замінити суму однакових доданків?, Тобто 5 ∙ 3=5

•                   Як називають числа 5 і 3? ( множниками)
•                   Як називають вираз 5∙ 3? ( добутком)

Аналогічно 3∙ 5 = 3+3+3+3+3+3;

                    7∙7+7+7+7;

                   1∙ 3= 1+1+1;

                   0∙ 5=0+0+0+0+0

У буквеному вигляді записують так:

а∙ в= а+а+а+а+а+...+а.

І кажуть:

 - Добутком числа а на натуральне число в, яке не дорівнює 1, називають суму, що складається з в доданків, кожний з яких дорівнює а.

2. Робота за підручником. Опрацювання правила, с. 106 ( Читання, повторення вголос).

3. Продовження бесіди:

- А якщо кількість доданків, тобто в, дорівнює 1. Доведеться розглядати суму, яка складається з одного доданка. Це в математиці не прийнято. Чому ж дорівнює добуток будь – якого числа і одиниці? ( тому самому числу)

- А якщо якесь число помножимо на нуль, то яке число отримаємо в добутку

 ( нуль).

•                   Отже, можна зробити висновки:

1. Якщо один із двох множників дорівнює 1, то добуток дорівнює іншому множнику.

2. Якщо один з множників дорівнює нулю, то добуток дорівнює нулю.

-Звернемось знову до нашого прямокутника, адже квадрати в ньому можна було порахувати і по – іншому ( 3+3+3+3+3=15 або 3∙5 = 15). Взагалі, від перестановки множників....( добуток не змінюється).

4. Усні вправи. Гра „Мовчанка”

3 ∙ 1 =         1 ∙ 17 =         45 ∙ 0 =            0 ∙  134 =      0  ∙ 0 =

15 ∙ 2 =       25 ∙ 4 =        32∙516=         418 ∙ 46 =    

( Діти легко розв’язують приклади з карток, крім двох останніх. Роблять висновок, що такі приклади розв’язати усно непросто, тому треба розв’язувати письмово)

5. Повторення правил письмового множення. Гра „Знайди помилку”.

- Я ці приклади для вас розв’язала. Та чомусь не впевнена у власних силах. Мені здається, що я десь  допустила помилку

   516                                  418

х                                     х

   32                                      46

  1022                               2508

+                                    +

  153                                 1672 

  2552                               4180

( учні розглядають, знаходять помилки, при цьому повторюють правила правильного оформлення прикладів,  при множенні в стовпчик)

 

6. Письмові вправи:

а) два учні одночасно працюють біля дошки, розв’язуючи приклади, в яких допущені помилки;

б) № 397 ( 3-6) – чотири учні працюють одночасно біля дошки.

в) Робота в парах - № 397 (7-9). Операція «Взаємодопомога».

7. Робота за підручником. Усні вправи -  №403 ( 1- 3), письмово - №403 (4-6)

8. Повторення порядку виконання дій у виразах, які містять дії І і ІІ ступеня. Виконання завдання № 399 (1) – хлопці; № 399 (2) – дівчата. Гра „Хто швидше?”

9. Робота над задачею - №405. ( Колективне обговорення, розв’язання учні записують самостійно із подальшою взаємоперевіркою)

 

V.  Підсумок уроку.

1. Бесіда:

- Над якою темою сьогодні на уроці ми працювали?

- Яку дію ми замінюємо дією множення?

- Як називаються числа при множенні?

- Що означає перший множник?

- На що вказує другий множник?

- Чому дорівнює добуток, якщо один з множників дорівнює нулю?

- Чому дорівнює добуток, якщо один з множників дорівнює одиниці?

- Що ж називають добутком числа a на натуральне число b?

- Сформулюйте переставну властивість множення.

2. Хвилинка цікавинка* (* -  за наявності вільного часу) – „З історії виникнення знаків множення”, „Таблиця множення на пальцях” ( Додаток 2)

- А чи відомо вам як з’явився знак множення?

( Якщо діти знайомі з даним питанням, то вони розповідають на клас, якщо ні – то повідомлення здійснює або вчитель, або наперед підготовлений учень)

 

VІ. Домашнє завдання – п.15, № 395( усно);

                                          №№398(1-5);400( 1-2) – І група;

                                          №№398( 6-9),404(3-4) – ІІ група.

Додаток 1

 

 

п

е

р

и

М

е

т

р

Н

у

л

ь

п

р

я

м

О

к

у

т

н

и

к

д

о

в

Ж

и

н

а

ш

і

с

т

д

Е

с

я

т

о

д

и

Н

с

і

м

Н

а

д

ц

я

т

ь

п

я

т

д

е

с

я

т

 

Додаток 2

 

Таблиця множення «на пальцях»

 

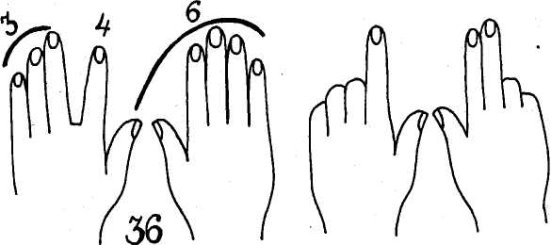
а) Множення на 9.

 

Покладемо кисті рук долонями на стіл і вважатимемо, що кож­ний палець має свій номер: перший зліва — 1, другий — 2, тре­тій —3 і т. д.

При множенні на 9 піднімаємо той палець, номер якого озна­чає множене. Кількість пальців зліва від піднятого означає число десятків добутку, а справа — число одиниць. Наприклад, щоб по­множити 4 на 9, піднімаємо четвертий палець. Зліва від нього — З пальці, а справа — 6. Отже, 4 • 9 = 36.

б) Множення чисел, більших від 5.

Нехай треба помножити 7 на 8. На лівій руці, зігнутій у кулак, розгинаємо 2 пальці (7 — 5 = 2), на правій — 3 пальці (8 — 5 = 3). Число розігнутих пальців обох рук додамо: 2 + 3 = 5. Це — десятки добутку. Числа зігнутих пальців перемножуємо: 2 • 3 = 6 — це оди­ниці.

Отже, 7 • 8 = 50 + 6 = 56. Аналогічно 6 • 8 = (1 + 3) • 10 + 4 • 2 = = 48; 6 • 6 = (1 + 1)  10 + 4 ∙ 4 = 36.

 

 

З історії виникнення знаків множення

 

У 1631 році англійський математик Оутред для позначення дії множення ввів косий хрестик: х. Знак множення •,крапку, запропонував німецький математик Лейбніц.

У XVIIст. Цей знак став загальноприйнятим.
Тепер, як ви знаєте,  використовують обидва знаки множення: і крап­ку, і косий хрестик. Крапкою користуються при множенні в рядок, а косий хрестик ставлять при множенні стовпчиком.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВОК

 

Проблема розвитку пізнавальної активності учнів є однією з найбільш актуальних в педагогічній теорії і практиці. Об’єктивна можливість розвитку пізнавальної самостійності зумовлена діалектичним характером навчального процесу. Як одна з властивостей навчальної діяльності школяра пізнавальна самостійність характеризується динамічним взаємозв’язком мотиваційного, змістового і організаційно-процесуального компонентів.

 

Взаємозв’язок пізнавальної самостійності з різними аспектами навчального процесу різноманітний. Тому в навчанні вона виявляється різнопланово: у процесі формування всебічно розвиненої особистості – як мета навчання; у процесі засвоєння знань умінь і навичок – як засіб підвищення усвідомленості та дійовості засвоюваного матеріалу. Водночас дидактика розглядає пізнавальну самостійність учня як результат ефективно організованого навчального процесу.

 

Таким чином у пізнавальній активності важлива її спрямованість, змістова характеристика. Отже, завдання вчителя полягає не тільки в тому, щоб розвивати природну допитливість школярів, а й навчити їх ставити пізнавальні запитання, які вимагають активного оперування знаннями, точного вибору способу дії, виробляють уміння міркувати в заданому їм напрямі: «від пізнавального запитання – до розв’язання пізнавальної задачі».

 

Навчання  учнів уміння ставити пізнавальні запитання передбачало систематичність, багаторазовість вправлянь і поступову самостійність учнів у цій роботі. В багатьох випадках на уроці ще переважає активність вчителя, який показує, розказує, ставить запитання, а активність учнів виявляється, як правило, у відповідях. А для розвитку пізнавальної активності школярів цікавих пізнавальних запитань учителя недостатньо, треба, щоб і в самих дітей виникали запитання, щоб вони вміли самостійно запитувати про нове, невідоме.

Отже, на уроках потрібно створювалися ситуації, які стимулювали б самостійність розумової діяльності школярів (приклади з життя та побуту). Учні мали б право захищати свою думку, наводили на її захист аргументи, докази, використовуючи при цьому здобуті знання. Вони мали б можливість задавати питання вчителю, товаришам. Крім того, вони мали б можливість ділитися і своїми знаннями з іншими, допомагали б товаришам долати труднощі, створювали б ситуації самоперевірки, аналізу особистих пізнавальних і практичних дій.

 

 

 

 

ЛІТЕРАТУРА

1. Аніпонова М. Активізація творчої діяльності учнів на уроках математики. // Математика. – 2009. – Червень. № 23. – С. 3–6.

2. Демиденко В.К. Виховання інтересу в учнів до навчання. – К.: Знання, 1978. – 183ст.

3. Дудач І. Активізація мислення учнів за допомогою інтерактивних технологій навчання. // Математика в школах України. – 2007. – № 33.– С. 8–11.

4. Забранська Н. Активізація пізнавальної діяльності учнів на уроках математики. // Математика. – 2004. – серпень № 31– 32. – С. 13–15.

5. Калашник І.І. Стимулювання особистісного розвитку учнів на уроках математики за допомогою інтерактивного навчання. // Математика в школах України. – 2010. – лютий № 5. – С. 2–6.

6. Киричук О.І. Виховання в учнів інтересу до навчання. – К.,1986 – 89ст.

7. Коберник О. М. Активізація навчально-пізнавальної діяльності школярів// Рідна школа, – № 12. – С. 55–60.

8. Колесникова Л.В. Нестандартні задачі – шлях до розвитку творчого мислення учнів. // Математика в школах України. – 2008.– № 8–9.–С.12–15.

9. Кулик Л. Декілька активних методик перевірки знань учнів // Математика в школах України. – 2005. – № 11. – С. 7–9.

10. Крисинська І.В. Розкладання многочленів на множники: Дидактичні матеріали з алгебри для 7–го класу. // Математика .– 2004. – № 45. – С. 8–11.

11. Петренко Р. Стимулювання творчої ініціативи учнів на уроках: опис досвіду. /Р. Петренко // Математика. – 2009. – Січень № 2. – С. 1–6.

12. Повстемська В. Активізація пізнавальної діяльності учнів на уроках математики як засіб підвищення результативності навчального процесу // Математика в школах України. – 2004. – № 34. – С. 2–5.

13. Прокопенко В.М. Використання інтерактивних технологій навчання на уроках математики. // Математика в школах України . – 2005. – № 26. – С. 3.

14. Пушкіна О. Активізація розумової активності та розвиток творчої

ініціативи на уроках математики. // Математика в школах України. – 2005. – № 31. – С. 2–5.

15. Шевченко Г. Форми активізації пізнавальної діяльності учнів на уроках математики в 5–9 класах. // Математика в школах України. – 2004. – № 30. – C. 2–4.

16. Щукина Г.И. Познавательные интересы в учебной деятельности школьников. – М.: Знание. – 1972. – 164 С.

17. Щукина Г.И. Активизация познавательной деятельности учащихся в учебном процессе. – М.: Просвещение. – 1979. – 160 С.

18. Шулигай С. Історія як засіб стимулювання пізнавального інтересу учнів на уроках математики. // Математика в школі. – 2009. – № 9. – С. 24–30.