Стаття:"Як будують графіки в Німеччині?"

У зв’язку з війною в нашій країні багато українських учнів опинилися в різних куточках світу. Вони продовжили навчання за програмами та методиками інших країн. Хочу поділитися досвідом побудови графіків лінійних рівнянь з двома невідомими в школах Німеччини. Вміння будувати графіки за таким алгоритмом дозволяють розв’язувати системи рівнянь.

Розглянемо приклад:

Спочатку кожне з рівнянь треба записати у вигляді функції: у=, де k є Z, n є N, m довільне число.

Маємо: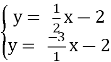

Побудуємо графік першого рівняння. Задаємо першу точку. Якщо х=0, то у=-2. Ця точка стає точкою відліку. Далі рухаємось праворуч на 2 клітинки і вгору на 1 клітинку. Отримали ще одну точку з координатами (2;-1). Проводимо пряму.

Чому так?

Проаналізуємо. Так як ми зафіксували першу точку, тепер взяли х=2, то знаменник коефіцієнта в рівнянні функції скоротився, а координата у змінилась на значення чисельника(якщо він додатний - рухаємось вгору, якщо від’ємний вниз)

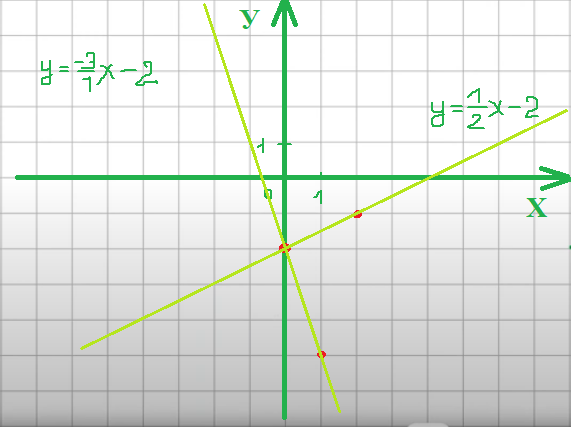
Аналогічно будуємо графік другого рівняння. Відмічаємо точку з координатами

(0;-2), фіксуємо. Від неї зміщуємось на 1 клітинку праворуч і на 3 вниз(від’ємний чисельник). Проводимо пряму.

Підписуємо графіки і визначаємо точку перетину: (0;-2)

Оригінальний метод побудови графіків може зацікавити учнів і розширить лінійку математичних інструментів розв’язування систем лінійних рівнянь графічним способом.