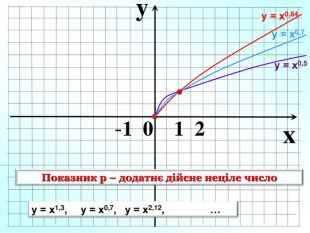
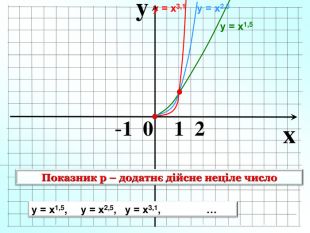
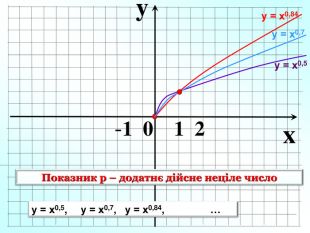
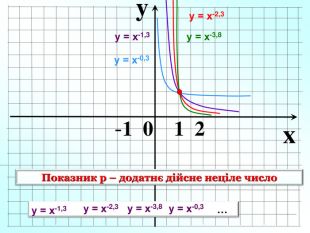
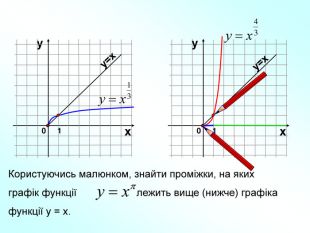
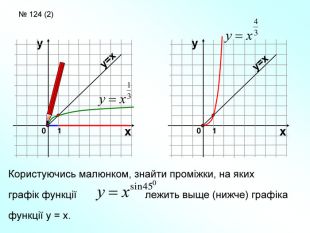
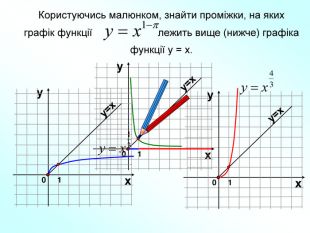
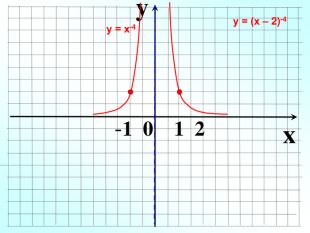
Степенева функція. Графік степене вої функції та ї властивості . Презентація

Cтепенева функція 10 клас Урок №1

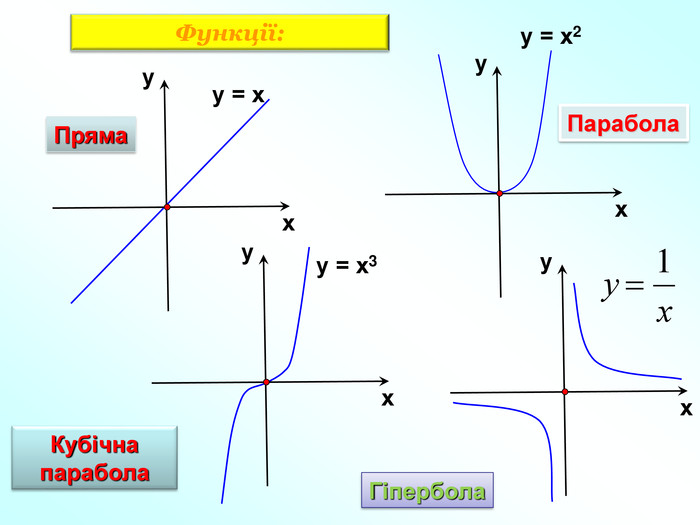
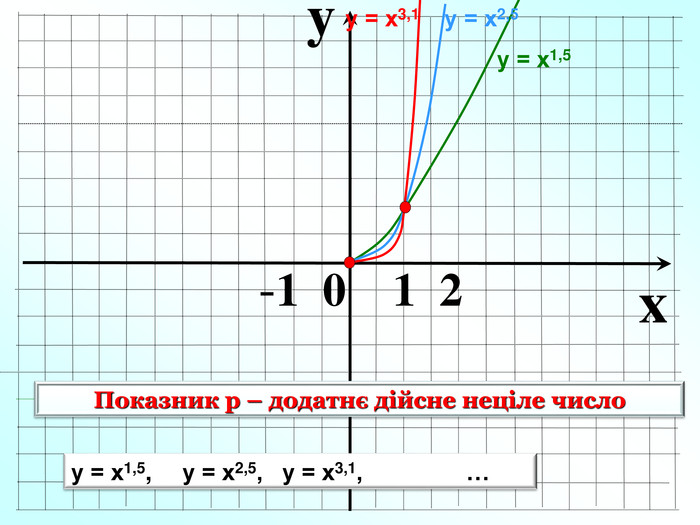
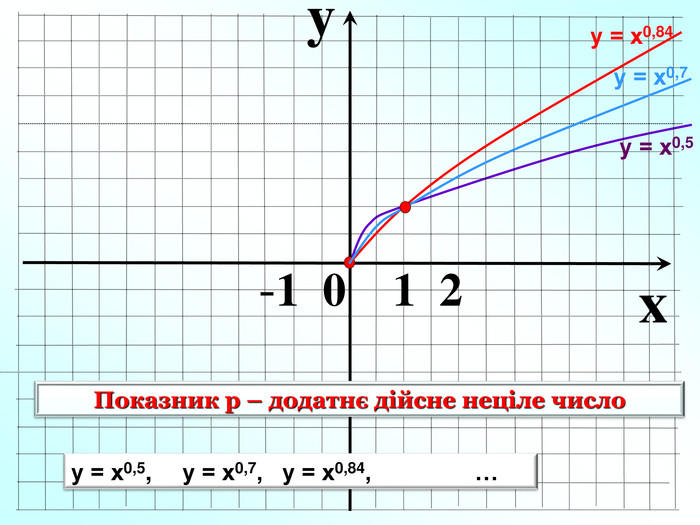
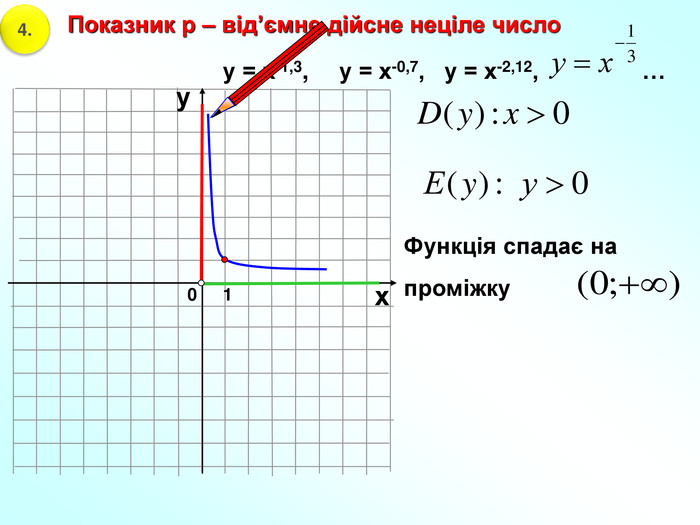
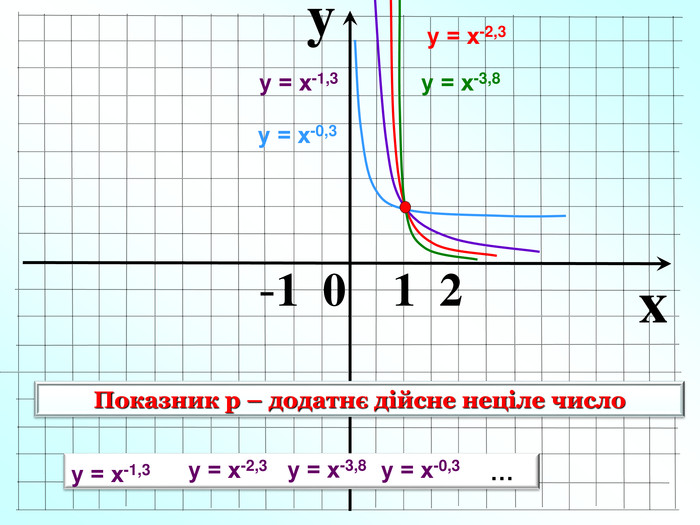
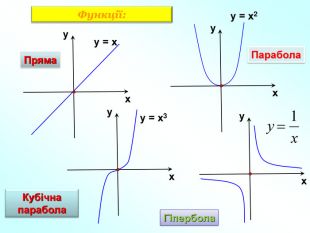
Пригадаємо: Функція – це залежність між … Множина значень функції- це всі значення … змінної. Способи задання функції. Область визначення функції- це всі значення … змінної Функція – залежність між двома змінними, при якій кожному значенню змінної х відповідає лише одне значення змінної у.

Функція – одне з найважливіших понять сучасної математики. Воно було введено у 17 столітті, коли у зв'язку з розвитком механіки у математику проникли ідеї зміни і руху. Французькі математики П'єр Ферма (1601-1665) та Рене Декарт (1596-1650) розглядали функцію як залежність ординати точки кривої від її абсциси. Термін «функція» (від латинського functio — виконання, звершення) для назви залежностей вперше ввів Готфрід Лейбніц (1646-1716). Він пов'язував функцію з графіками.

Давайте пригадаємо: Функція – це залежність між … Множина значень функції- це всі значення … змінної. Способи задання функції. Область визначення функції- це всі значення … змінної Функція – залежність між двома змінними, при якій кожному значенню змінної х відповідає лише одне значення змінної у.

Оберіть із заданих функцій лінійну Лінійні функції y = kх + b Вірно!

Оберіть із заданих функцій прямої пропорційності Функції прямої пропорційності y = kх Вірно!

Оберіть із заданих функцій квадратичну Квадратична функція y= ax2 +bx + c Вірно!

у = х х у у = х2 х у у = х3 х у х у Пряма Парабола Кубічна парабола Гіпербола Функції:

Всі ці функції є окремими випадками степеневої функції Функцію, яку можна задати формулою y = xn, де n ∈ Z, називають степеневою функцією з цілим показником.

Означення степеневої функції Наприклад: Функція y=хn , де n – задане дійсне число називається степеневою функцією

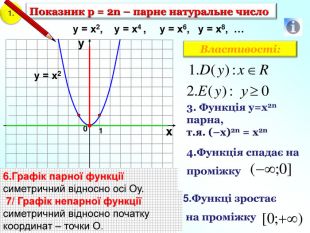
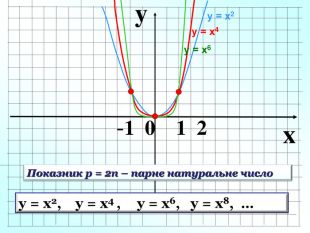
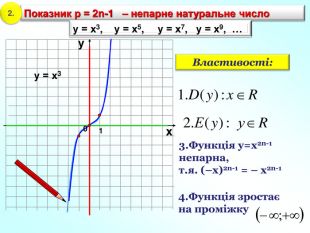
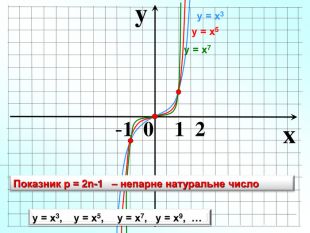
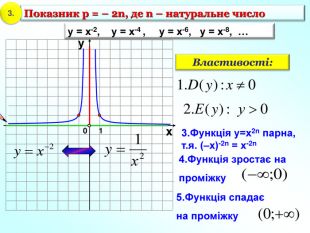
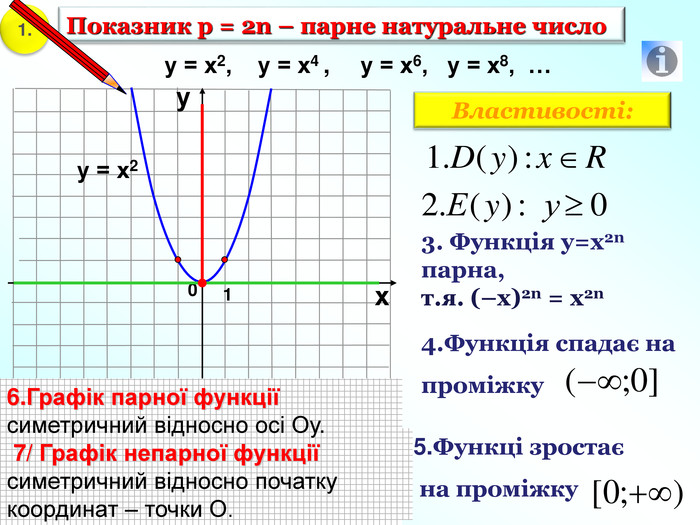
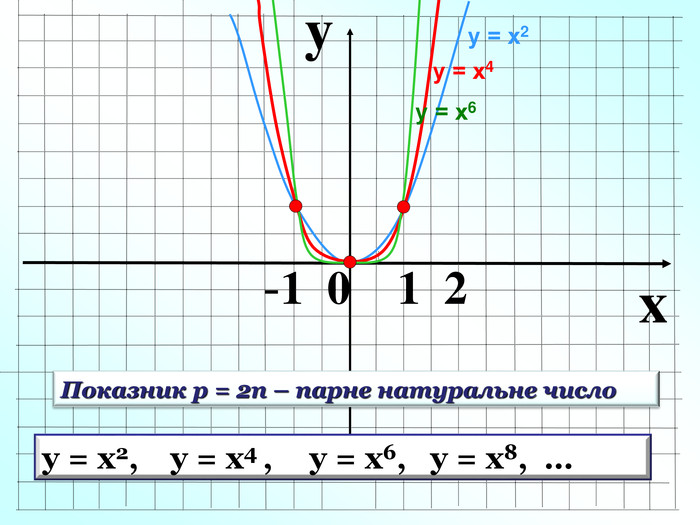
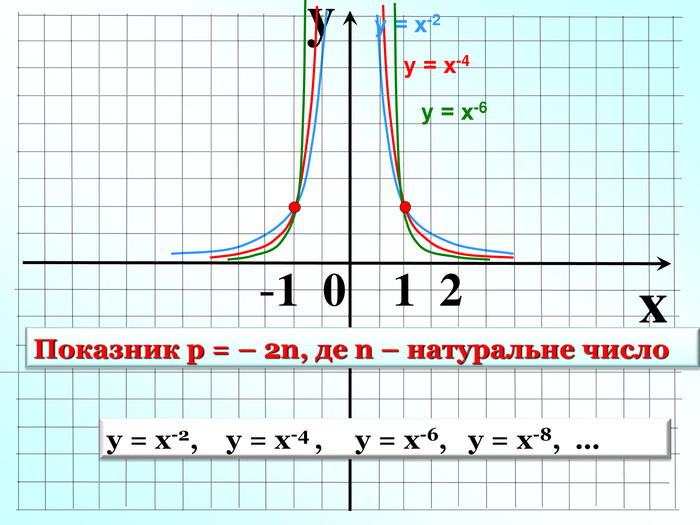
1. Показник р = 2n – парне натуральне число 1 0 х у у = х2, у = х4 , у = х6, у = х8, … у = х2 3. Функція у=х2n парна, т.я. (–х)2n = х2n 4.Функція спадає на проміжку Область визначення функції – значення, яких може набувати незалежна змінна х Область значень функції– множина значень , яких набуває залежна змінна у 6.Графік парної функції симетричний відносно осі Оу. 7/ Графік непарної функції симетричний відносно початку координат – точки О. 5.Функці зростає на проміжку Властивості:

y x -1 0 1 2 у = х2 у = х6 у = х4 Показник р = 2n – парне натуральне число у = х2, у = х4 , у = х6, у = х8, …

Показник р = 2n-1 – непарне натуральне число 1 х у у = х3, у = х5, у = х7, у = х9, … у = х3 3.Функція у=х2n-1 непарна, т.я. (–х)2n-1 = – х2n-1 0 4.Функція зростає на проміжку Властивості: 2.

y x -1 0 1 2 у = х3 у = х7 у = х5 Показник р = 2n-1 – непарне натуральне число у = х3, у = х5, у = х7, у = х9, …

Показник р = – 2n, де n – натуральне число 1 0 х у у = х-2, у = х-4 , у = х-6, у = х-8, … 3.Функція у=х2n парна, т.я. (–х)-2n = х-2n 4.Функція зростає на проміжку 5.Функція спадає на проміжку Властивості: 3.

y x -1 0 1 2 у = х-4 у = х-2 у = х-6 Показник р = – 2n, де n – натуральне число у = х-2, у = х-4 , у = х-6, у = х-8, …

5.Функція спадає на проміжку Показник р = – (2n-1), де n – натуральне число 1 0 х у у = х-3, у = х-5 , у = х-7, у = х-9, … 3.Функція у=х-(2n-1) непарна, т.я. (–х)–(2n-1) = –х–(2n-1) 4.Функція спадає на проміжку 4. Властивості:

y x -1 0 1 2 у = х-1 у = х-3 у = х-5 Показник р = – (2n-1), де n – натуральне число у = х-3, у = х-5 , у = х-7, у = х-9, …

0 Показник р – додатнє дійсне неціле число 1 х у у = х1,3, у = х0,7, у = х2,12, … Функція зростає на проміжку 5. Властивості:

y x -1 0 1 2 у = х0,5 у = х0,84 у = х0,7 Показник р – додатнє дійсне неціле число у = х1,3, у = х0,7, у = х2,12, …

y x -1 0 1 2 у = х1,5 у = х2,5 у = х3,1 Показник р – додатнє дійсне неціле число у = х1,5, у = х2,5, у = х3,1, …

y x -1 0 1 2 у = х0,5 у = х0,84 у = х0,7 Показник р – додатнє дійсне неціле число у = х0,5, у = х0,7, у = х0,84, …

0 Показник р – від’ємне дійсне неціле число 1 х у у = х-1,3, у = х-0,7, у = х-2,12, … Функція спадає на проміжку 4.

y x -1 0 1 2 у = х-1,3 у = х-0,3 у = х-2,3 у = х-3,8 Показник р – додатнє дійсне неціле число … у = х-1,3 у = х-2,3 у = х-3,8 у = х-0,3

Користуючись малюнком, знайти проміжки, на яких графік функції лежить вище (нижче) графіка функції у = х. у 0 1 х у=х 0 1 х у у=х

Користуючись малюнком, знайти проміжки, на яких графік функції лежить выще (нижче) графіка функції у = х. у 0 1 х у=х 0 1 х у у=х № 124 (2)

Користуючись малюнком, знайти проміжки, на яких графік функції лежить вище (нижче) графіка функції у = х. 0 1 х у у=х 0 1 х у у=х у 0 1 х у=х

y x -1 0 1 2 у = х-4 у = (х – 2)-4

y x -1 0 1 2 у = х-4 у = х– 4 – 3

y x -1 0 1 2 у = х-4 у = (х+1)– 4 – 3

y x -1 0 1 2 у = х-3 у = (х-2)– 3– 1

y x -1 0 1 2 у = (х+2)–1,3 +1 у = х-1,3

le-savchen.ucoz.ru http://ito.vspu.net/SAIT/inst_kaf/kafedru/matem_fizuka_tex_osv/www/Naukova_robota/data/Konkursu/2009_2010/boychyk_2009_2010/matematuka/matematuka.html http://www.oktyabrskiy-ruo.edu.kh.ua/nasha_biblioteka/mediateka/pidruchniki/ http://nsportal.ru/karatanova-marina-nikolaevna http:/ http://le-savchen.ucoz.ru/index/0-91 http://le-savchen.ucoz.ru/index/0-92 Список використаних джерел