Міністерство освіти і науки України

Відокремлений структурний підрозділ

«Запорізький фаховий електротехнічний коледж

Національного університету «Запорізька політехніка»

 

 

 

ЗАТВЕРДЖЕНО

Протокол засідання

ПЦК «Галузеве машинобудування» від  «_____»________2016р. №____ Голова ПЦК             А.О.Терлецька

 

 

 

 

 

 

ТЕХНІЧНА МЕХАНІКА

 

Блок 2 «Опір матеріалів» Збірник опорних конспектів лекцій для всіх технічних  спеціальностей

 

 

 

 

 

 

 

 

 

 

 

Викладач                                                                             Ігор ДУБОВСЬКИЙ

 

 

 

 

 

 

 

                                                                                                    2021                                       

Передмова

 Опір матеріалів є складовою частиною предмета «Технічна механіка»   і вивчається на всіх технічних спеціальностях коледжу згідно стандарту про вищу освіту (СВО). 

Об’єм навчальних годин на лекції, практичні заняття, лабораторні, розрахунково-графічні, самостійні і контрольні роботи у відповідності з навчальними планами і програмами спеціальностей  141«Електроенергетика, електротехніка та _{електромеханіка»}, 171«Електроніка»  та 133 «Галузеве машинобудування» суттєво відрізняється. Але це не впливає на якість вивчення сутності основних понять і законів опору матеріалів, таких як: характерних особливостей кожної деформації, умов міцності, трьох видів задач, закону пружності тощо. 

 На основі власного досвіду викладання автор пропонованого збірника пропонує низку текстів лекцій з блоку «Опір матеріалів», які можна вважати опорними конспектами для використання студентами при підготовці до занять, як додатковий матеріал для написання рефератів студентам заочного відділення, а також для передачі досвіду методики викладання предмета молодим колегамвикладачам.

 Цей збірник також призначений надати допомогу тим студентам, які пропустили лекції, щоб вони мали можливість самостійно опрацювати окремі теми опору матеріалів, подані у стислій і спрощеній формі.

 В збірнику наведено достатню кількість прикладів рішення задач на міцність з метою закріплення теоретичних понять та вмінь використовувати основні формули опору матеріалів. 

 Необхідно звернути особливу увагу на додаток А, де приведена таблиця, в якій показані внутрішньо предметні зв’язки опору матеріалів у вигляді формул, рисунків, основних понять і законів.

          

Зміст

                Вступ                                                                                                     4

1          Основні положення опору матеріалів                                                   5

2          Основні фактори, які впливають на міцність, жорсткість 

і стійкість деталей                                                                                           8

3          Внутрішні силові фактори. Метод перерізів для їх визначення при 

простих деформаціях                                                                                      9

4          Геометричні характеристики поперечних перерізів бруса

при різних деформаціях                                                                                  11

5          Поняття про механічні напруги                                                             12

6          Деформації розтяг і стиск. Загальні характеристики деформацій       16

7          Епюри поздовжніх сил і нормальних напруг                                        16

8          Закон Гука при розтягу і стиску, модуль пружності матеріалу           19

9          Механічні випробування матеріалів                                                      21

10     Три види напруг в опорі матеріалів − граничні, робочі і 

допустимі                                                                                                        24

11     Умова міцності при розтягу і стиску. Три види задач на міцність       26

12     Практичні розрахунки деталей на зріз і зминання                      29

13     Особливості розрахунку валикових зварних швів на зріз                    32

14     Деформація зсуву. Закон Гука при зсуві. Модуль зсуву            37

15     Деформація кручення                                                                             38

16     Дотичні напруги при крученні                                                    39

17     Умова міцності при крученні. Умова жорсткості при крученні          42

18     Три види задач при розрахунках на міцність при крученні                 44

19     Контактні наруги                                                                                     48

20     Деформація згин                                                                                      49

21     Епюри згинальних моментів                                                                  53

22     Осьові моменти опору перерізу при згині                                             55

23     Три види задач при розрахунках на міцність при згині              56

24     Раціональні перерізи балок при згині                                          57

25     Поняття про розрахунки на жорсткість при згині                      59

                Список літератури                                                                                 61

                Додаток А Опір матеріалів: внутрішньо предметні зв’язки                    62

          

Вступ

 Наука «Опір матеріалів» була започаткована у XVIIст. відомим італійським вченим Г.Галілеєм. Він першим запропонував розраховувати на міцність сучасні йому нескладні конструкції. З того часу ця наука постійно якісно розвивається і вдосконалюється, тому що без таких знань неможливо спроектувати будь-який відповідальний виріб. Наприклад: велосипед, автомобіль, підйомний кран, гідротехнічну або заводську споруду, вежу, нафтопровід, лінію електропередачі, житловий будинок, міст, морське судно, літак, підводний човен, вироби військової техніки, космічний корабель тощо.

 Авторами законів опору матеріалів, методів універсальних розрахунків, гіпотез, базових понять і практичних досліджень є такі відомі вчені, як Г.Галілей,

Р.Гук, Л.Ейлер, Д.Чернов, М.Белелюбський, Д.Журавський, Ф.Ясинський, О.Верещагін, Я.Бернуллі, Т.Юнг, К.Мор, Ф.Нав’є, О.Коши, А.Гріффітс,

П.Лагранж, А.Вьолер, Г.Герц та інші.

Опір матеріалів – це наука про інженерні методи розрахунків деталей машин та елементів споруд на міцність, жорсткість, стійкість і витривалість. Ці розрахунки необхідно виконувати для впевненості в тому, що виготовлена конструкція працюватиме надійно і довготривало, та одночасно  буде раціональною і матеріалоємною.

 Наука «Опір матеріалів» ґрунтується на теоретичних і на дослідницьких даних. Має зв’язок з такими науками, як фізика, матеріалознавство, математика, теоретична механіка.

 Традиційно з метою спрощення вивчення предмета його зміст поділяють на розділи, модулі і теми, які мають внутрішньо предметні зв’язки. В даному збірнику пропонується стислий зміст кількох тем даного блоку у вигляді опорних конспектів, складених на основі академічних видань з «Опору матеріалів» та власного досвіду автора з викладання цього предмета студентам денного та заочного відділень коледжу.

          

Основні положення опору матеріалів

Опір матеріалів – це інженерна прикладна наука, в якій вивчаються методи розрахунків деталей машин, механізмів, агрегатів, приладів, а також елементів різних споруд на міцність, жорсткість, стійкість і витривалість.

Метою розрахунків є забезпечення надійної і довговічної роботи будь-якого виробу чи конструкції в заданих умовах при найменших витратах матеріалу на їх виготовлення і найменшій їх вазі ще на стадії проектування. Надійною вважається деталь, яка не руйнується в заданих умовах роботи і не отримує пластичних деформацій.

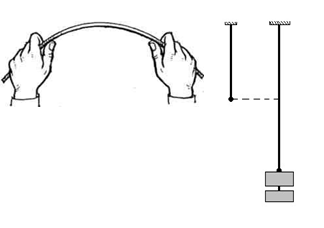Деформація – це зміна форми і розмірів тіла під дією зовнішніх навантажень – сил 

або моментів – пар сил (рис. 1)

         Залежно від того, як діють зовнішні                                                 

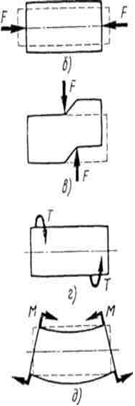
сили на деталь, вона може отримати такі  деформації (рис. 2) :

          а – розтяг    б – стиск

 в – зсув і зріз                                       Рисунок 1 – Приклади деформації  г – кручення                                        тіл при згині і розтягу  д – згин

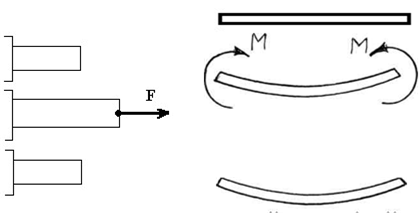Всі розрахунки в опорі матеріалів  справедливі в межах пружних деформацій. ПРУЖНИМИ називаються деформації, які повністю зникають після припинення дії  зовнішніх сил (рис. 3)

Пластичними (залишковими) називаються  деформації, які залишаються повністю або                 частково     після припинення          дії зовнішніх 

сил (рис. 4) 

 

Рисунок 2 – Види                 Рисунок 3 – Пружна           Рисунок 4 – Пластична  деформацій бруса                    деформація                         деформація Розрахункові схеми елементів конструкцій

 

Для спрощення розрахунків в опорі матеріалів всі деталі залежно від їх зовнішньої форми поділяють на 4 групи: брус, пластина, оболонка і масивне тіло.

БРУСОМ називають довгі і тонкі деталі, які можуть мати постійну або змінну товщину по довжині. Брус – це найбільш поширена в опорі матеріалів розрахункова схема деталей. Приклади бруса: вали, осі, стержні, колони, гвинти домкратів, шпонки, болти, заклепки, штифти, шпонки, свердла, різці, оправки фрез. Розрахунки пластин, оболонок і масивних тіл вивчаються в спеціальних розділах предмета.

 

 

 

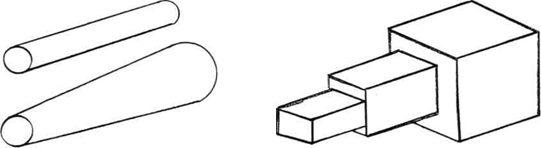
Рисунок 5 – Приклади розрахункової схеми багатьох деталей – бруса постійної і змінної товщини по довжині

 

Короткі відомості про міцність, жорсткість і стійкість деталей

 

Міцністюназивається здатність деталі чинити опір зовнішнім навантаженням (силам чи моментам) не руйнуючись і не отримуючи залишкових деформацій. На рис. 6 показані приклади двох виробів, які не витримали навантаження і зруйнувались.

 

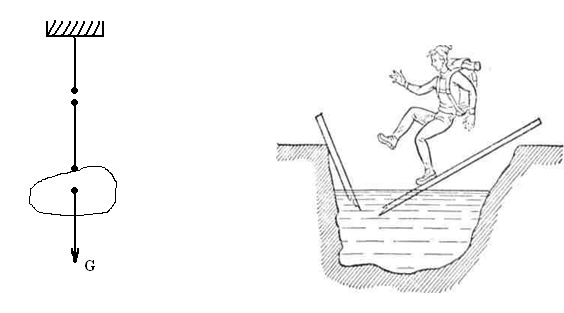
Рисунок 6 – Приклади не міцних виробів – вони зруйнувались

Жорсткістюназивається здатність деталі зберігати свою форму і розміри під дією зовнішніх зусиль. На рисунку 7 показана балка, яка прогнулась – змінила свою форму, але не зруйнувалась, і стержень, який розтягнувся, але не розірвався.

 

 

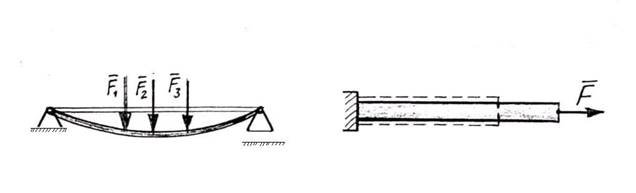
Рисунок 7 – Приклади не жорстких виробів

 

Стійкістю називається здатність деталі зберігати первинну прямолінійну форму рівноваги під дією осьових стискуючих зовнішніх сил. Розрахунки на стійкість називаються ще розрахунками на повздовжній згин, бо стійки прогинаються, викривлюються але не руйнуються (рис. 8).

 

 

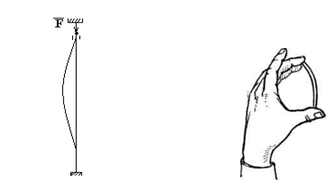
Рисунок 8 – Приклади виробів, які втратили стійкість, викривились

 

Для забезпечення нормальної роботи будь-якої конструкції необхідно, щоб всі її елементи задовольняли умовам міцності, жорсткості і стійкості при мінімальних її розмірах і вазі.

Підґрунтям науки про опір матеріалів є знання з теоретичної механіки, фізики, математики, технології матеріалів. Для перевірки теоретичних знань і гіпотез вчені використовують різноманітні випробування матеріалів і конструкцій в різних умовах на спеціальних випробувальних машинах і установках.

Знання з опору матеріалів вже давно запроваджені в практику в усіх галузях техніки: машинобудуванні, приладобудуванні, літакобудуванні, ракетній техніці, будівельній техніці – будівництві житлових споруд, мостів, веж, канатних доріг, ЛЕП, будівництві метрополітену. Ось чому опір матеріалів вивчають майбутні фахівці усіх галузей виробництва.  

Основні фактори, які впливають на міцність, жорсткість і стійкість деталей

 

Для розрахунків деталей на міцність, жорсткість і стійкість необхідно мати такі відомості:

− Матеріал, із якого виготовлена деталь (сталь, чавун, алюміній, пластмаса, деревина) і механічні властивості матеріалу (пластичний чи крихкий, які в нього значення границь міцності, як він поводить себе при різних деформаціях – розтягу, стиску, крученні, зрізі). Всі відомості про матеріали знаходяться в спеціальних довідниках;

− Розміридеталі: довжина, а також форма і розміри поперечного перерізу деталі. Форма поперечного перерізу може бути простою або складною, симетричною або несиметричною.

 

 

 

Рисунок 9 – Приклади форм поперечного перерізу деталей

 

− Навантаження– це зосередження сили, моменти (пари сил) чи

розподілене, навантаження, їх величина і місце прикладання до бруса (рис. 10)

 

 

 

Рисунок 10 – Приклади різних видів навантажень, прикладених до балки

 

− Деформаціядеталі – розтяг, стиск, зріз, кручення. згин, (рис. 2). Встановлено, що одна й та ж сама деталь неоднаково поводить себе при різних деформаціях.

Ці основні фактори відображаються в основних розрахункових формулах опору матеріалів, які мають назви: умова міцності, умова жорсткості, умова стійкості.

Наприклад, при розтягу умова міцності і умова жорсткості мають вид:

                                                = F / А               l = F *l/ Е* А  l.

Більш докладно ці формули будуть вивчатись далі.

Внутрішні силові фактори. Метод перерізів для їх визначення при

простих деформаціях

 

Зовнішні навантаження викликають сили протидії в матеріалі деталі, зумовлені міжмолекулярними зв’язками часток матеріалу.

Сили протидії є внутрішніми силами, які входять до складу основних формул при розрахунках на міцність і жорсткість.

Коли деталь навантажена тільки однією силою F чи моментом М, то внутрішній силовий фактор (ВСФ) за величиною дорівнює цій силі чи моменту на основі III закону Ньютона. В інших випадках треба застосувати метод перерізів, основою якого є умова рівноваги бруса до перерізу і його частин після перерізу. Відокремлена частина врівноважується тими ВСФ, прикладеними в центрі ваги бруса, які здатні зрівноважити дію зовнішніх навантажень: сили зовнішні – внутрішніми силами пружності, моменти зовнішні – внутрішніми моментами.

Всього існує шість ВСФ – три сили і три моменти у відповідності з шістьма рівняннями рівноваги для довільної просторової системи сил:

Fix = 0                Fiy = 0               Fiz = 0

Mix = 0                Miy = 0              Miz = 0

Розглянемо застосування методу перерізів на кількох прикладах при різних простих деформаціях бруса.

 

ПРИКЛАД 1

Брус навантажений тільки силами, які діють вздовж його повздовжньої осі Z. Сили F₁і F₂викликають деформації розтяг і стиск бруса, який в цьому випадку називають стержнем. Внутрішня сила пружності називається повздовжньою силою, позначається N_z - це ВСФ при розтягу і стиску.

Послідовність рішення: стержень треба розділити на солові ділянки ВС, CD, і т.д., в межах кожної ділянки провести один переріз, відокремити частину стержня, наприклад праву від площини перерізу, для зрівноваження прикласти в центрі ваги перерізу цієї частини ВСФ – сили N_z ,скласти рівняння рівноваги Fiz = 0і визначити із нього N_z .

 

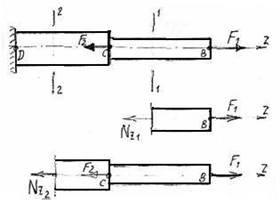
Fiz =F1 −N z1 = 0 N z1 =F1.

Fiz =F1 −F2 −N z2 = 0

N z2 =F1 −F2.

Рисунок 11- Приклад застосування метода перерізів при деформації розтяг і стиск Висновок

В межах ділянки ВС сила N_zдодатна – ділянка ВС розтягується; в межах ділянки CD сила N_z2від’ємна – ділянка CD стискується.

ПРИКЛАД 2 

Брус навантажений зовнішніми обертаючими (скручувальними) моментами

М₁та М₂,які закручують брус навколо осі Z. Внутрішній момент опору (або ВСФ) в цьому випадку називається крутним моментом, позначається M _z або M _k , а брус називається валом.

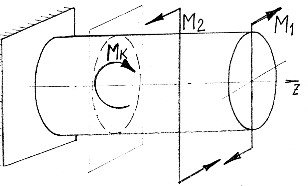Дано:

M₁= 25 кНм

M₂= 65 кНм

Для визначення Мкв показаному  перерізі бруса складемо рівняння рівноваги:

Miz = 0;   M₁ −M ₂ + M _k = 0

M _k = −M₁ + M ₂ = −25+ 65 = 40ВСФ   M _k = 40 кНм.

Рисунок 12 – Приклад застосування метода перерізів при деформації кручення 

Висновок

В показаному перерізі крутний момент  Мк, який зрівноважує зовнішні моменти М₁та М₂дорівнює 40 кНм.

ПРИКЛАД 3

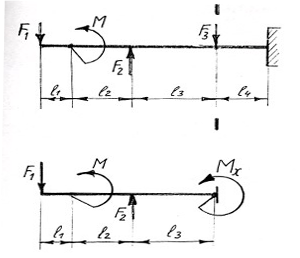Брус навантажений зовнішніми силами і моментами, які діють у вертикальній площині YZ і згинають брус, який в цьому випадку називається балкою. При згині простих балок основним ВСФ є згинаючий момент Мх. Дано :

F₁ = 5кН

F₂ = 7кН

F₃ =10кН M =14кнм

l₁ = 0.1м

l₂ = 0.2м

l ₃ = 0.3м

l₄ = 0.15м

 

 

Рисунок 13 – Приклад застосування метода перерізів при деформації згин

 

Для визначення Мх  в показаному метода перерізів при деформації перерізі балки складаємо рівняння згин рівноваги:

Mi = 0.

          

В рівняння входять моменти від сил, прикладених ліворуч від перерізу (праву частину балки відкидаємо згідно методу перерізів)

Mi = 0 ;

− F₁(l₁ +l ₂ +l₃)− M + F₂ *l₃ − M_x = 0

M _x = −F₁(l₁ + l ₂ + l ₃ ) − M + F₂ *l ₃

M _x = −5(0.1+ 0.2 + 0.3) −14+ 7*0.3 = −14.9кНм

Подібним чином визнаються моменти Мх біля кожної характерної точки зображеної балки.

Висновок

В показаному перерізі згинаючий момент Мх, який зрівноважує моменти від зовнішніх сил F₁, F₂і момента М дорівнює -14,9 кНм.

 

Геометричні характеристики, поперечних перерізів бруса при різних деформаціях

 

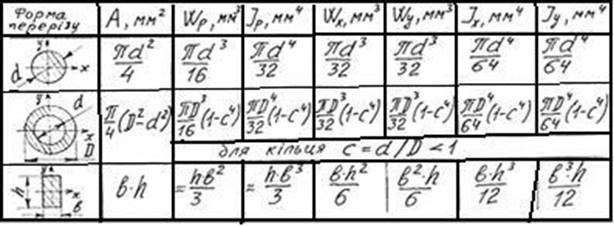
До геометричних характеристик перерізів (скорочено ГХП) відносяться величини пов’язані з формою поперечного перерізу деталі і розмірами перерізу. Для кожної форми перерізу деталі (круглої, квадратної і інших) ці величини визначаються за різними формулами (табл.1), а для прокатних профілів, знаходяться в спеціальних таблицях. Приведемо позначення і назви ГХП, які найбільш часто зустрічаються в опорі матеріалів:

А – площа перерізу, мм²або см²;

W_p - полярний момент опору перерізу, мм³або см³;

W_xабо W_y- осьові моменти опору перерізу, мм³або см³ ;

J _p- полярний момент інерції перерізу, мм⁴або см⁴ ;

J _x або J _y- осьові моменти інерції перерізу, мм⁴або см⁴ ;

Ці величини зустрічаються в основних формулах опору матеріалів – умовах міцності і умовах жорсткості. Приведемо приклади:

Умови міцності

                 − при розтягу і стиску                                      = N_z / A;

                 − при крученні                                                 _k = M_k /W_p _k;

                 − при зрізі                                                       _зр = Q/ A_зр _зр;

                 − при згині                                                       _зг = М _х /W_x  _зг .

Умови жорсткості

                 − при розтягу і стиску                                       l = N_z *l/E* Al;

                 − при крученні                                                   = M_k *l/G*J_p ;

                 − при згині                                                          ƒ= F *l³ /48E*J_x [ƒ].

Для двотавра №20 із таблиці сортамента:А=26,8см²; J _x = 1840см⁴ ; W_x =184см³; J _y =155см⁴ ; W_y =23.1см³.

Для швелера №20 із таблиці сортаменту: А= 23,4см²; J _x =1520см⁴ ; W_x =152см³; J _y =113см⁴ ; W_y =20.5см³.

Приклади формул для обчислення ГХП  приведені в таблиці 1:

Таблиця 1 −Приклади формул для обчислення ГХП різних перерізів

 

 

 

Поняття про механічні напруги

 

Під дією зовнішнього навантаження в матеріалі бруса виникають внутрішні сили опору, закон розподілу яких в загальному випадку навантаження (просторовою системою сил) має дуже складне математичне представлення. Тому для більш чіткого математичного представлення при розрахунках на міцність введено поняття про механічні напруги.

Напруга характеризує інтенсивність розподілу внутрішніх сил по площині поперечного перерізу бруса.

НАПРУГА – одне з основних понять опору матеріалів поряд з поняттями про деформації та ВСФ. Про важливість цього поняття свідчить той факт, що французькому вченому Анрі Нав’є (1785 – 1836), який першим сформулював це поняття і застосував у механічних розрахунках твердого тіла на міцність Академія наук призначила велику нагороду – титул барона, а уряд нагородив садибою.

Виведемо формули для визначення напруг.

Розглянемо брус, навантажений довільною системою сил F₁,F₂,F₃....F_n . Застосуємо для нього метод перерізів.

 

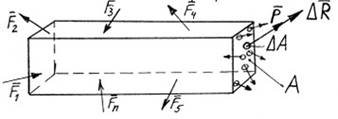
Рисунок 14 – Схематичне зображення механічних напруг в поперечному перерізі бруса

 

Виділимо в перерізі площиною А нескінченно малий елемент площиною  А – маємо право це робити, оскільки вважаємо матеріал неперервним. Рівнодіючу внутрішніх сил пружності в точці позначаємо R .

r

Поділимо R на А – визначимо інтенсивність внутрішніх сил, тобто середню напругу Р_сна площадці А:

pc ₌^R A

В точці напруга визначається із виразу:

p =lim → RA

                                                                                                           A     0

де p - повна напруга в точці.

Бачимо, що напруга p- величина векторна.

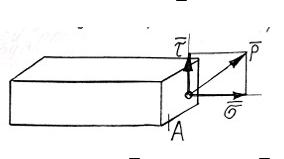
Розкладемо вектор повної напруги p на дві складові у площині – вектори _

і :

 

 

 

 

 

Рисунок 15 – Зв’язок між повною p , нормальною і дотичною напругами

 

p =+

 

Якщо відомі значення і , то повну напругу можна обчислити за формулою – теоремою Піфагора: 

p= p2 +2

Вектор _спрямований перпендикулярно до площини поперечного перерізу, тому напруга називається нормальною напругою. 

Вектор співпадає з площиною поперечного перерізу, тому називається дотичною.

Одиниці напруги:

                                                                                                      сила       Н

Напруга= площа = м₂ = Па(паскаль)^.

На практиці застосовують похідну одиницю напруги – мегапаскаль – МПа 1МПа = МН₂ = 1010₆⁶ммН =1ммН ,   або 1МПа =106Па.

_{2       2} м Тобто 1МПа =1Н / мм².

 

Розкладання повної напруги на нормальну і дотичну має цілком визначений фізичний зміст: у випадку, коли брус навантажений зовнішніми силами так, що отримує деформації розтяг, стиск або чистий згин – у поперечному перерізі бруса (стержня чи балки) діють тільки нормальні напруги . А коли брус навантажений так, що зовнішні сили викликають деформації зсув, зріз і кручення – діють тільки дотичні напруги .

Якщо на брус діє кілька навантажень (сил і моментів), то внутрішні сили, напруги, переміщення і деформації в будь-якому перерізі бруса визначають як суму величин, знайдених від кожного навантаження окремо. Цей принцип в опорі матеріалів має назву суперпозиції або принцип незалежності дії сил. Він стосується тільки конструкцій, деформації яких малі порівняно з їх розмірами і пропорційні діючим навантаженням, тобто в межах пружних деформацій.

Розглянемо закони розподілу нормальних і дотичних напруг по площині поперечного перерізу бруса при простих навантаженнях, які викликають будь-яку одну деформацію. Доведення саме такої схеми розподілу напруг і буде докладніше вивчатися далі. Для цього треба скористатись таблицею, де в узагальненому вигляді і для порівняння показані залежності між навантаженнями, деформаціями і відповідними напругами.

ПРИКЛАД 1 

Навантаження – зовнішня сила F,яка розтягує або стискує брус. Тут ВСФ – поздовжня сила N, яка викликає тільки нормальні напруги ; напруги розподіляються по площині поперечного перерізу рівномірно, тобто =const у будь-якій точці перерізу. Напруга обчислюється за формулою: N

=  ; знак напруги  залежить від знаку “плюс” чи “мінус” сили N : +N і + A

відповідають деформації розтяг ; -N і -- деформації стиск.

ПРИКЛАД 2 

Навантаження – зовнішня сили F, яка зсуває площину перерізу, може призвести до зрізу бруса. Тут ВСФ – поперечна сила Q, яка викликає тільки дотичні напруги ; напруги розподіляються по площині поперечного перерізу рівномірно, тобто при зрізі _зр = constу будь-якій точці перерізу.

Напруга _зр обчислюється за формулою:

Q

                                                                                                    зр = 

A_зр

ПРИКЛАД 3

Навантаження – зовнішні скручуючи моменти М або пари сил. В цьому випадку ВСФ – крутний момент Мк. Поперечні перерізи зсуваються відносно один одного навколо центра закручування – полюса. Дотичні напруги _к при крученні розподіляються нерівномірно по площині перерізу: _к  const, вздовж діаметра бруса (вала) _к змінюються по лінійному закону. Найбільше значення _к max обчислюється за формулою: M^k

_k max= W_p ПРИКЛАД 4

Навантаження – зовнішні сили F і моменти М, які згинають брус. При згині частина волокон балки розтягується, друга частина стискається, їх розділяє шар волокон, що не зазнає деформацій. Основний ВСФ при згині – згинаючий момент Мх. Нормальні напруги при згині  розподіляються нерівномірно по площині

ЗГ

перерізу: _зг  const,по висоті перерізу _ЗГ змінюються по лінійному закону, можуть бути із знаком “плюс” або “мінус”. Найбільше по модулю значення _ЗГ обчислюється за формулою: 

М х

                                                                                                    зг =       

W_x

          

ПІДСУМОК

Розрахункові напруги (РН) при будь-якій деформації бруса обчислюються за схемою:

 

                                                            ВСФ                Внутрішній_силовий_фактор

                                              РН =           =                                                                          

                                                            ГХП       Геометрична_ характеристика_перерізу

 

 

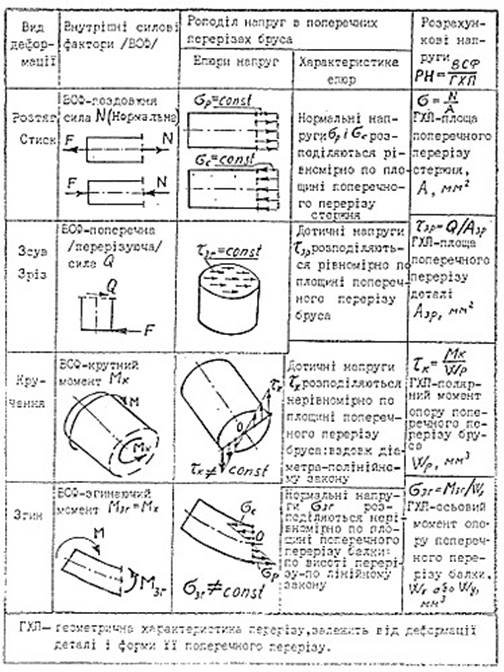
Таблиця 2 – Розподіл напруг в поперечних перерізах бруса при простих деформаціях

 

Деформації розтяг і стиск

 

Загальні характеристики деформації 

Брус навантажений тільки осьовими повздовжніми силами, отримує деформації розтяг або стиск. Такий брус ще називається  стержнем. При розтягу стержні видовжуються. При стиску – скорочуються. Абсолютна деформація стержня позначається l, вимірюється в “мм”. При розтягу lмає знак “плюс”, при стиску “мінус”. Деформацію lможна виміряти приладом (лінійкою, штангенциркулем) або обчислити за формулою Гука:

l = N_z *l/E* A

Пояснення до цієї формули будуть розглянуті далі. 

Внутрішнім силовим фактором при розтягу і стиску є повздовжня (нормальна) сила Nz , значення якої в будь-якому перерізі стержня визначається із формули:

Nz =Fiz

В правій частині формули враховуються проекції тільки тих зовнішніх сил  F₁,F₂,F₃ , які прикладені до залишеної (лівої чи правої) частини стержня.

В поперечному перерізі стержня виникають нормальні напруги , вектори яких перпендикулярні до перерізу. Напруги розподіляються рівномірно по площині перерізу (рис. 1), визначаються за формулою:

 

= N_z / A

 

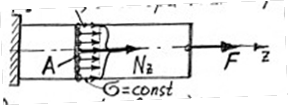
Рисунок 1 – Розподілення нормальних напруг  по поперечному перерізу стержня

 

Площа перерізу А залежить від форми перерізу:                                          і розмірів: 

в*h, d, a*a,і т.д.

Одиниці  Nz – Н (ньютон); одиниці А - м² або мм²Одиниці напруги:

                                                                                                      сила       Н

Напруга= площа = м₂ = Па(паскаль)^.

Похідна одиниця: 1МПа =10⁶Па =1Н / мм²Скорочене МПа – це мегапаскаль.

При розрахунках на міцність будь-якої деталі треба розрахувати значення напруги в її матеріалі – це буде далі показано на прикладах.

 

Епюри поздовжніх сил і нормальних напруг

 

Для наочності розрахунків в опорі матеріалів прийнято будувати спеціальні графіки – ЕПЮРИ ВСФ і напруг по довжині бруса. Епюри будуються в масштабі, в проекції під розрахунковою схемою до задачі. Епюри Nz і пов’язані між собою. Епюра

застосовується для визначення небезпечної ділянки стержня – по величині _мах , для

перевірки міцності стержня і для визначення деформації кожної ділянки стержня − l_і .

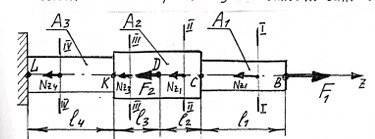
Приклади застосування методу перерізів при розтягу і стиску трьохступінчатого стержня, побудови епюри Nz і епюри , визначення деформації стержня l Умова прикладу і вихідні дані до розрахунків (рис. 2):

F₁ =12kH F₂ = 42kH

A₁ = 200мм²

A₂ = 300мм²

А₃= 240мм²

l₁ =150мм

l₂ = 75мм

l₃ = 90мм

l₄ =170мм Е = 2*10⁵МПа

Рисунок 2 – Розрахункова схема стержня до прикладу

 

Рішення 

Виділяємо на осі стержня z характерні точки В, С, D, K, L  і силові ділянки ВС, CD, DK, KL. В межах кожної ділянки проводимо перерізи – I, II, III, IV, відкидаємо ліву частину, а залишену праву частину зрівноважуємо силою N_zi - ВСФ при розтягу і стиску - Nz1, Nz2 , Nz3 , Nz4 .

Складаємо рівняння, із яких визначаємо N_zi :

В межах ділянки ВС                                  N_z1=   F₁ =12kH (розтяг ділянки );

                                                CD                              N_z2 = F₁ =12kH ;

 DK                             N_z3 = F₁− F₂= 12 −42 = −30 кH (стиск ділянки);  KL                         N_z4 = F₁− F₂= 12 -42 = − 30 кH.

Вибираємо масштаб, будуємо епюру Nz  в проекції під розрахунковою схемою. Додатні значення відкладаємо вгору від осі епюри, від’ємні – вниз. Масштаб вибираємо довільний, наприклад 10кН/см. Зразок оформлення епюри Nz приведений на рис. 3.

Визначаємо нормальні напруги в межах кожної ділянки стержня :

В межах ділянки ВС₁ = N_z1 / A₁ =12*10³ /200= 60H / мм² = 60МПа;

 СD ₂ = N_z2 / A₂ =12*10³ /300= 40H / мм² = 40МПа;  DK ₃ = N_z3 / A₂ =−30*10³ /300=−100H / мм² =−100МПа;  KL ₄ = N_z4 / A₃ =−30*10³ /240=−125H / мм² =−125МПа .

Звертаємо увагу, що знаки величин Nz і співпадають.

Вибираємо заново масштаб для побудови епюри в проекції під розрахунковою схемою і епюрою Nz. Масштаб епюри довільний, наприклад 40МПа/см. Зразок оформлення епюри приведений на рис. 3.

Визначаємо абсолютну деформацію ділянок l, мм:

Деформація ділянки ВС l₁ = N_z1 *l₁ / E* A₁ =12*10³ *150/2*10⁵ *200= 0.045;

СD l2 = Nz2 *l2 / E* A2 =12*10³ *75/2*10⁵ *300= 0.015;

DK l₃ = N_z3 *l₃ /E* A₂ =−30*10³ *90/2*10⁵ *300=−0.045;

KL l₄ = Nz₄ *l₄ /E* A₃ =−30*10³ *170/2*10⁵ *240=−0.106.

Звертаємо увагу, що знаки величин Nz і lспівпадають.

Визначаємо загальну деформацію стержня lзаг:

l_заг =l_і =l₁ +l₂ +l₃ +l₄ = 0,045+0,015−0,045−0,106=−0,091мм

Епюри повздовжніх сил Nz і нормальних напруг у відповідності з попереднім розрахунками до прикладу (рис. 3):

 

 

 

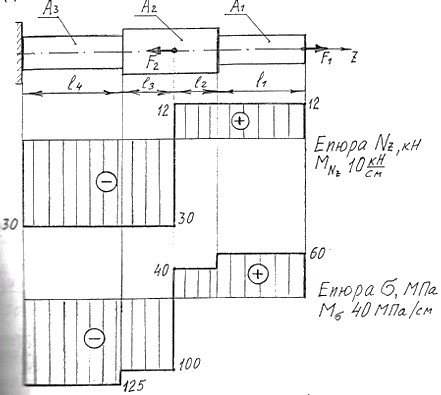
Рисунок 3 – Зразки епюр Nz і до прикладу

 

Висновки

− Ділянки ВС і CD розтягуються. 

− Ділянки DK і KL стискуються. 

− Напруги зворотно пропорційні площам поперечних перерізів стержня.

− Знаки Nz і співпадають. 

− На епюрі Nz стрибки тільки в точках прикладання сил F₁,F₂і в затисненні (точка L).

− На  епюрі стрибки під всіма характерними точками B, C, D, K, L.

− Епюра служить для визначення небезпечного перерізу стержня: в даному випадку це ділянка KL, в межах якої найбільше значення напруги по модулю - _мах = 125 МПа: вірогідність руйнування стержня на ділянці  KL найбільша.

− На ділянках  BC і CD стержень видовжився.

− На ділянках DK і KL стержень скоротився.

− Загальна деформація стержня – скорочення на 0,091 мм.

− Для висновку про міцність стержня необхідно порівняти _махз допустимою напругою : якщо _{мах } - стержень міцний.

Закон Гука при розтягу і стиску. Модуль пружності матеріалу

 

В 1660р.англійський вчений Роберт Гук відкрив залежність між навантаженням – зовнішньою силою F та деформацією l. Ця залежність прямо пропорційна: F~ l.(рис. 4)

Поділимо силу F на площу перерізу А , а lподілимо на початкову довжину

l стержня:

F

 =- нормальна напруга; A l

 =- відносне видовження,

l

де l, мм – абсолютне видовження (або скорочення)

 

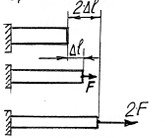
Рисунок 4 – Пропорційна залежність між силою F і деформацією l

 

Сучасна математична форма запису закону Гука має вид:

= Е*

(нормальна напруга пропорційна відносному видовженню .

Закон Гука є основним законом в опорі матеріалів і носить назву “закон пружності”, тому що справджується при всіх деформаціях.

Закон Гука має обмеження – до досягнення напруги – границі пропорційності _(рис. 5)

пц

 

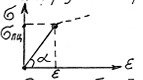
Рисунок 5 – Графічне зображення закону Гука

 

Величина Е – дуже важлива механічна характеристика матеріалу, називається модулем повздовжньої пружності матеріалу, або модулем пружності I роду, або модулем Юнга (значення модуля Е для технічних розрахунків встановив у 1800р. англійський вчений Томас Юнг.)

- величина безрозмірна, одиниці напруг   - МПа із закону Гука  виходить, що одиниці Е – теж МПа . У випадку, коли =1, тобто l=l- видовження 100%, Е =, це значить, що модуль Е дорівнює напрузі   в деталі, якщо вона видовжиться в два рази. Із рисунка видно, що   tg=/; Із закону Гука маємо:  =/; Виходить, що Е = tg.

Основний фізичний зміст модуля пружності Е: він характеризує здатність матеріалу протидіяти пружним деформаціям при розтягу і стиску, інакше характеризує жорсткість матеріалу. Числові значення модулів Е для різних технічних матеріалів визначені і знаходяться в довідниках для інженерів і конструкторів. Модуль Е треба знати при розрахунках деталей та елементів конструкцій на жорсткість при розтягу, стиску і згині.

 

Приклади значень модуля Е, МПа:

Матеріал

Сталь                                                                           (1.9.....2.2)*10⁵( 200000МПа)

Чавун                                                                           (0,9.....1,6)*10⁵ 

Мідь, латунь, бронза                                                     (1...1,3)*10⁵ 

Алюміній                                                                     (0,7...0,75)*10⁵( 70000МПа)

Деревина                                                                     (0,9...1,5)*10⁴

Цегла                                                                           (0,3...0,5)*10⁴

Бетон                                                                           (1...3)*10⁴(10000МПа)

Текстоліт                                                                     (0,4...0,6)*10⁴

Гетинакс                                                                      1*10⁴

Капрон                                                                         (0,7....1,0)*10³( 700МПа)

Гума                                                                           8(8МПа)

 

З цієї таблиці видно, що гума чинить дуже слабкий опір у порівнянні із сталевими деталями:

                                                                                        Ест            2*105

                                                                                                  =            = 25000разів.

                                                                                        Е_гум                   8

Така велика різниця пояснюється різною внутрішньою будовою цих матеріалів. Найбільше значення модуля Е має алмаз – для нього Е = 12*10⁵ МПа: алмаз має жорсткість більшу в 6 разів, ніж сталь!

Виведемо формули для розрахунку абсолютного видовження l стержня постійної товщини.

Запишемо закон Гука:  = Е*,

 

де = F/A,  МПа = Н / мм² ; = l/l.

                                                                                  F            l                      F *^l

                 Підставимо в закон Гука:  = E * звідкіля l =    , мм – це і є формула Гука.

                                                                                  A             l                       E *l

Тут добуток Е*А означає жорсткість перерізу; величина ЕА/l означає жорсткість стержня при розтягу чи стиску.

З формули Гука видно, що деформація lзалежить від навантаження – сили F і початкової довжини lпрямо пропорційно, а від модуля Е і площі поперечного перерізу А – зворотно пропорційна. Ось чому деталь із гуми значно видовжується під дією невеликих сил.

Деформація стержня розтяг чи стиск залежить від напряму дії зовнішніх сил

F₁,F₂,F₃ . В межах кожної ділянки визначають ВСФ – повздовжні сили N₁, N₂ , N₃за формулою:

Ni =Fiz

 

Якщо при розрахунках значення lвийде додатнім – стержень видовжиться; якщо  lвийде від’ємним – стержень скоротився. Для багатоступінчастого стержня його деформація визначається за формулою:

n

l = l_i = l₁ +l ₂ +l ₃....

i=1

 

Механічні випробування матеріалів

Розв'язання задач, що розглядаються у курсі опору матеріалів, можливе лише при наявності результатів .експериментального дослідження механічних властивостей різних матеріалів конструкцій.

Найважливіші механічні властивості металу визначають випробуванням металевого зразка на розтяг. Для випробування звичайно виготовляють стандартні циліндричні зразки, форма яких показана на рис. 6. 

 

 

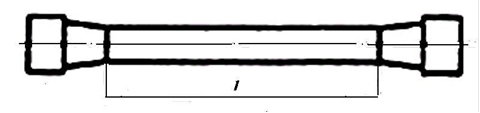
Рисунок 6 – Зразок для випробування на розтяг

 

У кожного зразка є головки для закріплення його в захватах машини. Довжина середньої частини зразка l називається розрахунковою. Перед випробуванням вимірюють розрахункову довжину зразків і їхні діаметри, потім зразки закріплюють в захватах випробувальної машини, розтягують, поступово збільшуючи навантаження і відмічають силу та відповідне цій силі видовження l. За формулами(2) і(3) знаходять значення напруги  і відносної деформації . Випробування проводять аж до розриву зразка.

= N/ A  (2)

= l/l  (3)

Діаграму розтягу будують у системі осей координат. По осі абсцис відкладають відносну деформацію , а по осі ординат —нормальну напругу .  Наносячи на рисунок одержані точки і з'єднавши їх плавною лінією, одержимо криву, яка називається діаграмою розтягу (рисунок 7).Іноді діаграму розтягу креслять автоматично спеціальним приладом під час випробування. В цьому випадку з барабана приладу в кінці випробування знімають вже готову діаграму, що виражає залежність між розтягуючою силою F і видовженням зразка l. Ця діаграма подібна до діаграми, наведеної на рис. 7, а , і відрізняється від неї лише масштабом. Однак діаграма розтягу в координатах , краще відображає фізичні властивості матеріалу, оскільки вона не залежить від геометричних розмірів випробуваного зразка. 

          

 

 

 

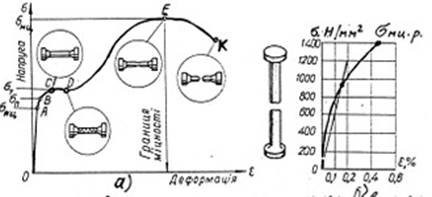
Рисунок 7 – Діаграми розтягу низьковуглецевої сталі а) і чавуну б)

 

На рис. 7, а подано діаграму розтягу зразка з м'якої сталі. Аналізуючи цю діаграму, помічаємо, що на ділянці ОА вона являє собою пряму  лінію. Це означає, що на даній ділянці напруга збільшується пропорційно деформації. Чим більша деформація, тим більша і напруга. І, навпаки, зі збільшенням напруги, зі збільшенням навантаження відповідно зростає і деформація.   Інакше,   на ділянці ОА матеріал підлягає закону Гука. Потім в точці А лінія починає викривлятись, що свідчить про  порушення прямо пропорціональної залежності між напругами і деформаціями.

 

Найбільша напруга, до якої вірний закон Гука, тобто деформації у зразку зростають пропорційно навантаженню, зветься границею пропорціональності (_ПЦ

).

 

На діаграмі дуже близько до границі пропорціональності розміщено границю пружності. Якщо припинити випробування в той момент, коли напруга в матеріалі ще не досягла границі пружності, і розвантажити зразок, то він повністю відновлює свої початкові розміри, тобто деформація повністю зникає. Матеріал поводить себе як абсолютно пружний. Якщо ж границя пружності буде перебільшена, то після розвантаження зразок вже не набуде своїх попередніх розмірів, залишається так звана пластична, або залишкова, деформація.

 

Границя пружності(_П )−це найбільша напруга, до якої у зразку не виникають залишкові деформації.

 

Далі на діаграмі видно майже горизонтальну ділянку СО. Це свідчить про те, що деформації зростають, а напруга залишається незмінною. Стан матеріалу в цьому випадку називають текучістю, напругу у зразку − границею текучості (_Т ), а ділянку

СО −ділянкою текучості. Метал нібито втратив здатність протистояти зусиллю розтягування. В цей час можна помітити помутніння добре відполірованої поверхні зразка, а при досить сильному збільшенні −виявити сітку ліній, нахилених під кутом 45^° до осі зразка. Ці лінії називають лініями Чернова за ім'ям видатного російського вченого-металурга Д. К.Чернова (1839 −1921), який вперше їх спостерігав. Вони являють собою сліди зсувів частинок матеріалу.

При розтяганні зразків з високовуглецевої сталі, міді, дюралюмінію на діаграмі немає ділянки текучості, як для м'якої (низьковуглецевої) сталі. В таких випадках замість фізичної границі текучості визначають умовну границю текучості −напругу, при якій залишкове видовження зразка становить 0,2% від його початкової довжини (позначається  0,2). Після стадії текучості матеріал знову починає чинити опір деформації (ділянка ОЕ діаграми), проте тепер вже деформації зростають не пропорційно напругам (навантаженням), а значно швидше. Спостерігаючи за зразком, легко помітити, що він в одному місці починає різко звужуватись, утворюється так звана шийка. З появою шийки опір зразка зменшується. 

 

Умовна напруга, що відповідає найбільшому навантаженню за час випробування матеріалу, називається границею міцності (_мц )  або тимчасовим опором(_ТМ ).

 

Умовною ця напруга називається тому, що вона віднесена до початкової площі перерізу зразка, тобто до площі перерізу до деформації. З цієї причини величина тимчасового опору завжди виявляється значно нижчою за дійсну напругу при розриві.

Шийка зразка поступово витягується, стає все тоншою і, нарешті, при напрузі, що відповідає точці К на діаграмі, зразок розривається.

Такі матеріали, як чавун, цегла, бетон і деякі, інші,  розриваються без помітного видовження і без утворення шийки. Ці матеріали називаються крихкими. Крихкість −негативна властивість матеріалу. За поступовою деформацією деталі з пластичного матеріалу при надмірному збільшенні навантаження можна судити про наближення моменту поломки, в той час, як деталі з крихких матеріалів ламаються раптово. При випробуванні на розтяг зразків з крихкого матеріалу звичайно знаходять величину границі міцності. На рис. 7,6 подано діаграму розтягу чавуну, на діаграмі відсутня ділянка текучості, і навіть при малих напругах, тобто в початковій стадії навантаження, спостерігається відхилення від закону Гука.

Оскільки при випробуванні зразків з крихких матеріалів утворення шийки не спостерігається і площа поперечного перерізу майже не змінюється, то границя міцності, на відміну від тимчасового опору пластичних матеріалів, виявляється за

величиною майже рівною дійсній напрузі при  розриві; основна  характеристика, (МЦ .Р ).

Крихкі матеріали, які погано чинять опір розтяганню, здатні витримувати великі стискаючі навантаження. В лабораторії звичайно вивчають крихкі матеріали, піддаючи їх сильному стисканню, визначають _мц.ст.

Якщо конструкціям доводиться працювати одночасно на стиск і на розтяг, їх виготовляють з двох матеріалів, що мають потрібні властивості. Наприклад, залізобетон являє собою поєднання сталі і бетону. В ньому сталь (арматура) відмінно протидіє розтяганню, а оточуючий її бетон −стисканню.

Три види напругв опорі матеріалів – граничні, робочі і допустимі

В опорі матеріалів розрізняють три види напруг: граничні (небезпечні), робочі (фактичні) і допустимі.

Робочі напруги − це фактичні напруги, які в дійсності мають місце в елементі навантаженої конструкції.

Граничною −це напруга, при якій матеріал руйнується, або в ньому виникають помітні залишкові деформації. Для пластичних матеріалів роль граничної напруги відіграє границя текучості (_Т ). Для крихких матеріалів, при розтяганні (стисканні) яких явище текучості не має місця, за граничну напругу повинна бути прийнята границя міцності на  розтяг (_М.Р ), або границя міцності на СТИСК (_{М .С} ) .

Очевидно, що для забезпечення міцності елементів конструкції треба, щоб виникаючі в них напруги були менші за граничні. Нагадаємо, що виникнення в деталі залишкових деформацій розглядається як порушення її міцності. Не можна, наприклад, працювати на токарному верстаті, у якого зігнуто шпиндель.

Якщо робочі напруги в деталі близькі до граничних (хоч і менші за них), міцність деталі гарантувати не можна. Тому при розрахунках на міцність робочі напруги порівнюють не з граничними, а з допустимими, які становлять деяку частину від граничних.

Допустимі напруги можна визначити як найбільші напруги, при яких забезпечується безпечна тривала і надійна робота елемента конструкції. Позначають їх [].

Величина, що показує, яку частину від граничних напруг становлять допустимі, називається нормативним (заданим) коефіцієнтом запасу міцності і позначається [п]: ^гран

                                                                                            = .

n

Питання вибору нормативного коефіцієнта запасу міцності дуже складне. Вкажемо лише основні фактори, що впливають на вибір величини коефіцієнта запасу міцності: а) точність визначення діючих навантажень і застосовуваних методів розрахунку; б) ступінь однорідності застосовуваного матеріалу і вивченість його властивостей; в) відповідальність деталі.

Дуже важливо правильно вибрати коефіцієнт запасу міцності. Беручи дуже малий коефіцієнт запасу, ми тим самим приймаємо дуже високі допустимі напруги і можемо в результаті мати неміцну конструкцію. З іншого боку, беручи великий коефіцієнт запасу міцності, ми забезпечимо більшу міцність конструкції, проте конструкція буде не економічною і важковаговою. Надлишок міцності зумовлює тим самим перевитрату матеріалу, збільшує вагу машин, знижує їх продуктивність і економічність.

На початку розвитку машинобудування ще не вміли досить точно розраховувати деталі машин і споруд на міцність, і для забезпечення надійності конструкції обирали дуже великий коефіцієнт запасу міцності. Отже, завищений коефіцієнт запасу міцності компенсував недостачу знань в галузі опору матеріалів. Тому його іноді називали «коефіцієнтом незнання». Наприклад, 40 років тому при розрахунку будівельних конструкцій інженери вважали для сталі Ст.3 допустимою напругу не більше 100 Н/мм². Зараз конструкції з сталі цієї марки, за винятком мостів, розраховують з допустимою напругою 160Н/мм², тобто коефіцієнт запасу міцності зменшився більш як у півтора рази.

          

Боротьба за зниження коефіцієнта запасу міцності тривав і в наш час. Перед машинобудівною промисловістю стоїть завдання дальшого зниження запасу міцності створюваних конструкцій і машин при одночасному збільшенні їх міцності. Міцність машин збільшують, застосовуючи в машинобудуванні пластмаси, леговані і низьколеговані сталі, жаротривкі сплави, термічну обробку тощо. Кожний новий успіх вчених у галузі опору матеріалів −це удар по «коефіцієнту незнання», це нові можливості зменшення ваги і вартості машин при одночасному збільшенні їх міцності і довговічності.

У зв'язку з різноманітністю умов, при яких працюють елементи конструкцій, нормативний коефіцієнт запасу міцності в кожному окремому випадку задається або вибирається за відповідними спеціальними довідниками.

 

Допустимі коефіцієнти запису міцності при статичних навантаженнях:

− для пластичних матеріалів                                [п]= 1,4…2,0; − для крихких матеріалів                                               [п]= 2,5…5,0;

                 − для крихкопластичних                                           [п]= 1,6…2,5.

Допустимі напруги для деяких матеріалів:

− сталь Ст. 3 і Ст.4		Р  =  С  = 140…170 МПа;
− сталь Ст. 5		Р  = С  = 175…210 МПа;
− сталь 45		Р  =  С  = 180…210 МПа;
− дюралюміній		Р  = С  = 70…150 МПа;
− чавун СЧ 12-28		Р  = 20…30 МПа     С  = 70…110 МПа;
− чавун СЧ 21-40		Р  = 35…55 МПа    С  = 160…200 МПа;
− текстоліт		Р  = 30…40 МПа    С  = 50…90 МПа.

Названі напруги: РОБОЧА ( або фактична, або розрахункова ), ГРАНИЧНА (

_Т або _МЦ )^{, ДОПУСТИМА}   ^або   будуть зустрічатись при розрахунках на міцність при всіх деформаціях (розтяг, стиск, зріз, кручення, згин).

 

Умова міцності при розтягу і стиску. Три види задач на міцність

 

Міцність бруса, що зазнає осьового розтягання (стискання), забезпечена, якщо додержана умова



 

Фізичний зміст ЇЇ полягає в тому, що для забезпечення належної міцності елемента конструкції робочі (фактичні) напруги не повинні перевищувати допустимих...

Підставляючи у попередній  вираз значення з формули 2, одержимо

 

N

 =   . A

 

Як видно з цього виразу, міцність бруса, що розтягується, не залежить від форми його поперечного перерізу.

Геометричною характери стикою міцності в цьому випадку є площа поперечного перерізу А. Чим більшою є ця площа (при однаковому навантаженні), тим менші нормальні напруги і, отже, тим більша міцність бруса.

Залежно від завдання розрізняють три типи розрахунків на міцність: а) п е р е в і р н и й ;

б) п р о е к т н и й ;

в) розрахунок допустимого навантаження .

Коротко охарактеризуємо кожний з цих розрахунків.

При перевірному розрахунку вважаються відомими навантаження, матеріал (а отже, допустима або гранична напруга) і розміри елемента конструкції. Потрібно перевірити, чи дійсно робочі напруги в поперечних перерізах цього елемента не  будуть перевищувати допустимі: .

У деяких випадках визначають фактичний коефіцієнт запасу міцності п і порівнюють його з нормативним

^гран

                                                                                                    n = .



Умова міцності буде підтверджена, якщо  п>[п].

Перевірний розрахунок застосовують, зокрема, при експертизі виконаних проектів.

Проектний розрахунок, як видно з назви, має місце при проектуванні конструкцій. В цьому розрахунку задано навантаження і матеріал (допустиму напругу), потрібно визначити необхідну площу поперечного перерізуй.

Із умови міцності виходить, що

N

                                                                                                      A  



Розрахунок допустимого навантаження провадять за відомими розмірами поперечного перерізу бруса і з врахуванням допустимої напруги матеріалу; в цьому випадку визначають найбільше навантаження, яке може витримати цей брус. Із умови міцності виходить, що

 

N A.

 

Цей розрахунок застосовується при зміні режимів технологічних процесів, коли необхідно підвищити навантаження існуючого обладнання і, отже, потрібно знати їх гранично допустиме за умовою міцності значення.

 

Розглянуті три види розрахунку проілюструємо прикладами.

ПРИКЛАД 1 

У похилому стержні АВ зображеного кронштейна під дією зовнішніх сил F виникає реактивна сила S , яку можна назвати зусиллям розтягування, або внутрішньою силою пружності N. Стержень АВ виконаний із двох рівнобічних кутників № 7, 5.Допустима напруга для сталі _Р  =160МПа.

Перевірити міцність стержня АВ, якщо N = 280 кН.

Рішення 

Ця задача I  виду, тому запишемо умову міцності 

_Р = N / A

Площу перерізу стержня визначимо за допомогою таблиць сортаменту:

площа перерізу одного кутника А₁ = 8,78см² , площа перерізу двох кутників

 

А= 2*8,78=17,56см² =1756 мм²

 

Обчислюємо робочу (фактичну, розрахункову) напругу в матеріалі кутників:

 

 

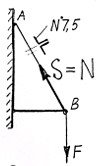
Рисунок 8 −До прикладу 1

 

 

Порівняємо розрахункову напругу _Р і допустиму _Р  :

159 < 160, тобто _Р <_Р  .

Умова міцності виконується – стержень АВ – міцний.

ПРИКЛАД 2 

Визначити потрібний діаметр стальної дротини, яка навантажена зовнішньою силою F = 80 кH. Допустима напруга _Р  = 160 МПа.

 

 

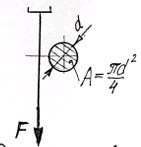
Рисунок 9 −До прикладу 2

Рішення 

Ця задача II виду, тому що невідомий розмір деталі, який забезпечить її міцність в даних умовах. Спочатку знайдемо необхідну площу поперечного перерізу А із умови міцності:

 

N

                                                                                                      A  .



 

Потрібний діаметр знайдемо із формули площі круга

 

A = d2 , 4

звідкіля                                              d  ^4A .



Обчислення:                            А  80*10³ /160= 500мм² .

 

                                                                                      d      4500 = 25мм.

3,14

 

Відповідь

Дротина повинна мати діаметр d = 25мм.

Практичні розрахунки деталей на зріз та зминання

 

Деформацію зріз зазнають деталі, які в робочому стані навантажені поперечними зовнішніми силами: це штифти, заклепки, “чисті” болти (поставлені в отвори без щілин), осі, пальці, шпонки , уступи, валикові зварні шви (рис 1)

 

 

Рисунок 1 – Приклади деталей, які зазнають зріз.

В поперечних перерізах цих деталей виникають дотичні напруги зрізу _ЗР(рис

2).

 

 

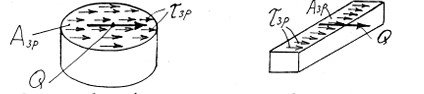
Рисунок 2 – Дотичні напруги _ЗР розподіляються рівномірно по площині поперечного перерізу А_ЗР .

Внутрішній силовий фактор при зрізі – поперечна сила Q, яка обчислюється за формулою: Q =_ЗР * А_ЗР

 

Умова міцності при зрізі

Розглянемо заклепку, що з’єднує два листи, які зазнають розтягання (рис 3). При достатній величині розтягуючи сил і недостатній міцності заклепки її стержень може зрізатись вздовж перерізу mn (рис 3)

Практичні розрахунки на зріз ґрунтуються на таких основах припущеннях:

а) у поперечному перерізі виникає тільки поперечна сила

б) внутрішні сили розподіляються по перерізі рівномірно

Оскільки внутрішні сили діють у площі перерізу, то при зрізі виникають дотичні напруги. Виходячи з сформульованих вище припущень, ці напруги можна визначити так:

Q

 

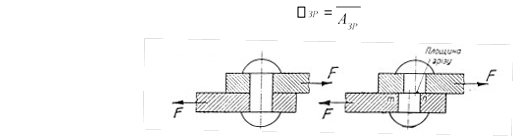
Рисунок 3 – Листи розтягуються, а заклепки зазнають зріз

 

Q

                Умова міцності при зрізі: _ЗР =  _ЗР 

АЗР

          

Відбиває той фізичний факт, що для забезпечення належної міцності елемента, що працює на зріз, робоча (фактична) напруга _ЗРне повинна перевищувати допустиму напругу на зріз _ЗР  Допустима напруга на зріз 

 

_ЗР = (0,750,80)_Р ,

 

де _Р − допустима напруга на розтяг для того самого матеріалу.

Використовуючи умову міцності можна розв’язувати ті самі три види задач, що й при розтягу (стиску):здійснювати перевірний розрахунок, проектний розрахунок і визначити допустиме навантаження.

 

Три види задач при розрахунках на зріз

I                      вид – ПЕРЕВІРНИЙ полягає в перевірці умови міцності:

 

ЗР = Q/ Азр  ЗР ,

 

Якщо розрахункова напруга _ЗР  _ЗР - деталь міцна, якщо _ЗР  _ЗР- умова не справджується, деталь не міцна.

II                   вид – ПРОЕКТНИЙ – полягає у визначені розмірів поперечного перерізу деталей, які забезпечать її міцність. Спочатку визначають необхідну площу зрізу А_ЗРіз умови міцності :

А_ЗР = Q або А_ЗР = F ,

                                                                                         ЗР           ЗР 

 

а потім залежно від форми поперечного перерізу деталі обчислюють діаметр d, або розміри в і l і т.ін. Для заклепок, штифтів, болтів, пальців, які мають круглий поперечний переріз, А_ЗР =d ² /4, а для призматичної шпонки A_ЗР = b*l . Відповідно знаходяться d і в:

 

4A^зр A^зр A^зр d  ;  b =   або  l =  .

                                                                                                   l                  b

 

III                вид – визначення допустимого навантаження:

 

F A_ЗР *_ЗР .

 

Основні відомості про розрахунках на зминання.

Зріз звичайно супроводжується зминанням матеріалу в місцях контакту стичних елементів конструкцій. Зминання можна розглядати як місцеве стискання контактуючих поверхонь. Так наприклад поверхня під головкою болта від дії сили F (рис 4) зминається.

          

 

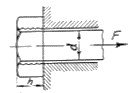
Рисунок 4 −Зминання поверхні під головкою болта

 

При розрахунку на зминання вважають, що сили взаємодії (тиску) між стичними деталями, що перебувають під навантаженням, рівномірно розподілені по поверхні контакту і перпендикулярні (нормальні) до цієї поверхні. Рівнодійну цих сил позначимо літерою F. Тиск, що припадає на одиницю площі контактної поверхні, зветься напругою зминання і позначається _ЗМ . З припущення про характер розподілу тиску по поверхні контакту випливає, що  F

                                                                                                  ЗМ =  ,

AЗМ

де _ЗМ −площа зминання (рис 5).

 

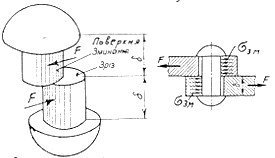
Рисунок 5 – Нормальні напруги при зминанні _ЗМ

 

З цього ж припущення випливає (виводу ми не наводимо), що коли контакт здійснюється по поверхні напівциліндра (як це має місце, наприклад, при роботі заклепки), де розрахункова площа зминання _ЗМ дорівнює площі діаметрального перерізу, тобто добуткові діаметри циліндричної поверхні на її висоту (рис 6).

 

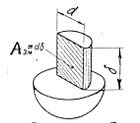
Рисунок 6 −Розрахункова площина зминання

 

Площа зминання шпонки обчислюється за формулою:

А_ЗМ  0,5*h*l ,

де h – висота шпонки;  l – довжина шпонки.

Умова міцності на зминання:

F

                                                                                          АЗМ = ЗМ ;

A_ЗМ

де _ЗМ  - допустима напруга на зминання. Звичайно приймають

 

_ЗМ = (1,72,0)_Р 

 

де _Р − допустима напруга на розтягання для з’єднуваних елементів,

залежить від матеріалу.

Розрахунки на зминання проводять як перервні за умовою міцності:

 

ЗМ = F / AЗМ  ЗМ .

 

Розглянемо кілька прикладів розрахунків деталей і з’єднань на зріз і зминання, які ще раз покажуть, що опір матеріалів – це прикладна інженерна наука.

 

 

Особливості розрахунку валикових зварних швів на зріз

 

На зріз розраховуються напусткові зварні шви, які називаються валиковими. Якщо шов розташований перпендикулярно до напряму діючої сили F – шов називають лобовим, якщо паралельно силі F – називають фланговим (рис 7).

 

 

Рисунок 7 – Приклади зварних з’єднань деталей валиковими напустковими швами

− лобовим і фланговим

 

Умова міцності має вид:

 

ЗР = F / AЗР  ЗР ,

 

де _ЗР  для зварних швів приймають залежно від технології зварювання; наприклад, при ручному зварюванні електродом звичайної якості приймають _ЗР = 0,6_Р . Тут _Р=_Т /n, n=1.35...1.70 − допустимий коефіцієнт запасу міцності, _Т- границя текучості зварюваного матеріалу.

Площа зрізу _ЗРваликових зварних швів залежить від довжини L і катета шва К (рис 8). Для тонких листів К=(товщині листів).

          

 

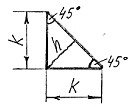
Рисунок 8 −Форма перерізу валикового зварного шва

 

Тріщина валикових зварних при їх руйнуванні співпадає з бісектрисою прямого кута h , тому _ЗР = L*h, де h = k *sin45^o = k *0.707, або _ЗР = 0.7kL

За умовою міцності для зварних швів на зріз можна вирішувати три види задач.

I                     вид – ПЕРЕВІРНИЙ – основна формула _ЗР          =         ^F             _ЗР 

0.7kL

II                  вид – ПРОЕКТНИЙ – полягає у визначенні необхідної довжини шва L або довжини напустку деталей l_Н у відповідності з кресленням до конструкції , основна

                                                                               F                               L

розрахункова формула: L    , потім l_Н =   (рис 7).

                                                                  0.7k_ЗР               2

Визначену довжину l_Нтреба закруглити до числа, кратного 10.

III               вид – визначення допустимого навантаження F:

F AЗР *ЗР = 0,7kLЗР 

Приклад 1 

Вантажний ланцюг прикріплюється до гака (рис 9) з допомогою пальця з нарізаним кінцем (на рисунку показано окремо).Визначити з умови міцності на зріз (

_ЗР = 35МПа) потрібний діаметр пальця, якщо гак і ланцюг розраховані на піднімання вантажу G=30кН.

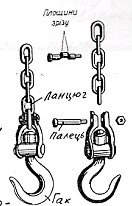
Рисунок 9 −До прикладу 1

 

Рішення

 

Це задача проектного виду, тому що треба знайти діаметр пальця d.

Із умови міцності спочатку знайдемо площу зрізу А_ЗР :

А_ЗР  G/_ЗР 

А_ЗР =30*10³ /35=857мм²

          

 

Із рисунка 9 видно, що палець має 2 площини зрізу, тому необхідну площу перерізу одного зрізу обчислимо так:

 

А_ЗР = А_ЗР /2 = 428,5мм²

 

Діаметр пальця знайдемо із формули площі круга:

 

Aзр = d2 ; d  4Aзр = 4428,5 = 23,4мм.

                                                                          4                              3,14

 

Приймемо найближче стандартне значення d =24 мм.

Приклад 2

Визначимо силу F, необхідну для пробивання круглого отвору  діаметром   d

= 30мм в сталевому листі товщиною =10мм, якщо границя міцності сталі при зрізі _МЦ.ЗР =360МПа. Підібрати матеріал пуансона (рис 10)

 

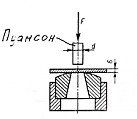
Рисунок 10 −До прикладу 2

 

Рішення

Це задача III виду, тому що необхідно визначити сили F. Розрахункова формула:

F = AЗР* МЦ.ЗР

 

Площу зрізу Азр визначимо як площу бокової поверхні циліндра діаметром d і висотою :

А_Зр =d *= 3.14*10*30 = 942мм² .

Руйнівна сила: Fp =942*360=338000Н=338кН

Визначимо напругу стиску в пуансоні

d2

                                                                                       _с = F_p / A = F_p / ,

4

3 / 3.14*102 H c = 338*10 4 = 478мм2 = 478МПа .

Напруга стиску в пуансоні _с велика, тому для пуансона треба використати леговану сталь з великим значенням _МЦ , наприклад сталь марки Х12, для якої _МЦ

=1500МПа. Фактичний запас міцності n буде:

n =_МЦ /_с =1500/478=3,15

Приклад 3

Визначити необхідну довжину  l напусткового валикового зварного шва

(рис 7), якщо сила F=130кН, катет шва К=10мм, допустима напруга на зріз зварного шва _ЗР =90МПа.

Рішення 

Це задача проектного виду, тому що треба визначити довжину шва l .

Із умови міцності на зріз зварного шва з урахуванням кількості швів (по  рис 7 швів 2) знайдемо довжину l : ЗР = F  ЗР або F  ЗР .

                                                                            A_Зр                                               0.7* K *l*2

Довжина l : 

                                                                                   F                      130*10³

                                                           l                             =                          = 103мм

                                                                0.7*k *2*_ЗР   0,7*10*2*90

Приймемо найближче стандартне значення l =110 мм.

Приклад 4

Визначити необхідний діаметр d осі зображеного шарнірно – зварного з’єднання (рис 11), якщо сили, які розтягують стержні 1 і 4 F=280кН, перевірити деталі 2 і 4 на зминання. Вісь 3 виготовлена із сталі 45, для якої _ЗР = 90МПа, якої

_ЗМ =250МПа, товщина деталі 2 S = 20мм, товщина деталі 4 в перерізі Б-Б S=10мм.

 

 

 

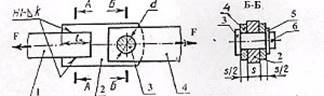
Рисунок 11 −Складальне креслення шарнірно-зварного з’єднання до прикладу 4

 

Рішення.

Сили F викликають зріз осі 3, тому діаметр осі визначимо із умови міцності при зрізі, враховуючи кількість зрізів і = 2. Отримане значення d закруглимо до стандартного числа:

 

                                                                             F                                F

                                                                  _ЗР  _ЗР , або   d₂ _ЗР,

                                                                        2* A                                

2*

4

 

звідкіля розрахункова формула має вид:

 

                                                                 d          4F       =     4280103 = 44,5мм.

                                                                           2_зр               23,1490

Приймемо d = 45мм.  Умова міцності на зминання: 

 

F

                                                                                          зм =  ЗМ ,

AЗм

тут А_ЗМ = d *s.

 

280*10³

_ЗМ =  = 311250 − умова не виконується. В цьому випадку збільшимо 45*20 діаметр осі – приймемо d=55мм.

280*10³

_ЗМ =  = 254250 −, але перевищення незначне, в межах допустимих 10%, 55*20 тому призначаємо d = 55мм.

 

 

 

 

 

 

Деформація зсуву. Закон Гука при зсуві. Модуль зсуву

Уявимо собі процес перерізання листа жерсті ножицями для металу. Сили, що діють з боку лез на метал, утворюють пару сил з дуже малим плечем (рис. 1,а). Ця пара зумовлює перекіс листа між точками прикладання сил. При достатній величині цих сил настає зріз.

Деформація, що передує зрізу і полягає у спотворенні прямих кутів в елементі тіла, називається зсувом.

Величина зміни вказаних кутів зветься кутом зсуву і позначається літерою  (рис. 1, б). Кут зсуву є мірою деформації зсуву і вимірюється в радіанах.

 

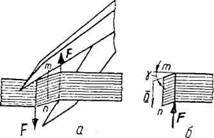
Рисунок 1 – Зсув

 

Для вивчення дії внутрішніх сил при зсуві застосуємо метод перерізів. Мислено розсічемо лист на ділянці між лезами ножиць на дві частини і, відкинувши одну з них, розглянемо рівновагу частини, що залишилась (рис. 1, б). Для того щоб ця частина була в рівновазі, внутрішні сили повинні бути напрямлені вздовж перерізу в бік, протилежний силі F. Крім того, їх рівнодійна - поперечна сила Q −повинна дорівнювати за величиною силі F (однієї цієї умови не досить, оскільки сили утворюють пару із згинальним моментом; однак згинальною дією цієї пари нехтують через те, що її плече дуже мале).

Припускають, що внутрішні сили розподіляються вздовж перерізу рівномірно. Оскільки вони діють в площині перерізу, то зумовлені ними напруги будуть дотичними. З припущення про рівномірність розподілу внутрішніх сил вздовж перерізу випливає, що

                                                                                                     Q                 F

                                                                                            = , або  = .

                                                                                                      A                 A

Між дотичними напругами і кутом зсуву існує залежність, подібна закону Гука при розтягу (стиску)

 = G.

Величина G, що входить в цей вираз, зветься модулем зсуву, або модулем пружності другого роду. Модуль зсуву залежить від фізичних властивостей матеріалу й характеризує його жорсткість при зсуві.

Між трьома пружними сталими: модулем поздовжньої пружності E, коефіцієнтом Пуассона і модулем зсуву G існує залежність, яку ми наводимо без виводу: E

                                                                                                  G = .

2(1+)

Наприклад, для сталі при _=0,25 одержимо

E

G =  = 0,4E . 2(1+ 0,25)

Отже, для сталі G  0,810⁵H / мм²; (E = 210⁵H / мм²).

Вираз  = Gявляє собою математичний запис закону Гука при зсуві: дотичні напруги прямо пропорціональні куту зсуву.  

 

Деформація кручення

Основні гіпотези. Кручення зазнають вали машин, осі залізничних вагонів, пружини, болти при закручуванні гайки ключем тощо. Дослідимо механізм деформації кручення. Уявимо брус круглого поперечного перерізу, жорстко затиснутий одним кінцем (рис. 2). У площині вільного торця цього бруса прикладемо пару сил з моментом m. Цей момент називатимемо скручувальним на відміну від моменту внутрішніх сил, який називають крутним.

Уявлення про характер деформації бруса можна дістати, якщо скручувати гумову модель цього бруса. Якщо на циліндричну поверхню розглядуваної моделі до деформації нанести сітку з малих квадратиків, утворюваних поперечними колами і поздовжніми твірними, а на вільний торець бруса - його радіус (рис. 3, а), то після деформації можна помітити таке (рис. 3, б):

 

 

 

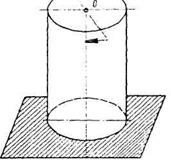
Рисунок 2 −Брус жорстко затиснений одним кінцем

 

 

 

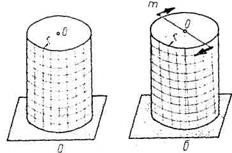
Рисунок 3 −Брус до та після деформації кручення

1)                 квадратні клітинки перетворюються у ромбічні, тобто елементи на поверхні бруса зазнають деформації зсуву;

2)                 контури кіл не викривлюються, і вони залишаються перпендикулярними до осі бруса;

3)                 відстані між кожними двома сусідніми колами внаслідок деформації не змінюються;

4)                 радіус, нанесений на торцевому перерізі, в процесі деформації не викривлюється.

Можна вважати, що й в середині бруса картина деформації не буде істотно відрізнятися від картини на поверхні. За результатами досліду можна твердити, що при крученні брус поводить себе так, нібито він складений з окремих жорстких кружечків, насаджених центрами на спільну вісь. При деформації всі ці кружечки, не змінюючи своєї форми, розмірів і взаємних відстаней, повертаються один відносно одного.

Описані спостереження дають підставу для прийняття таких гіпотез (припущень):

1)                 всі поперечні перерізи в процесі деформації залишаються плоскими і перпендикулярними до осі бруса (гіпотеза плоских перерізів);

2)                 відстані між поперечними перерізами внаслідок деформації не змінюються; 3) радіуси поперечних перерізів не викривлюються.

Вся теорія кручення бруса круглого поперечного перерізу ґрунтується на цих гіпотезах. Їхня прийнятність підтверджується добрим узгодженням результатів теорії з результатами досліду, практики.

 

Дотичні напруги при крученні

Напруги і деформація (основні формули). Як указано вище, деформація кручення полягає в тому, що поперечні перерізи бруса, залишаючись плоскими й перпендикулярними до його осі, повертаються один відносно одного і свого початкового положення до деформації. Найбільшого повороту зазнає переріз на вільному торці бруса. Кут повороту радіуса будь-якого поперечного перерізу зветься кутом закручування. Деформацію кручення можна уявити як результат ряду зсувів внаслідок поворотів сусідніх поперечних перерізів бруса.

Твірні циліндричної поверхні бруса що скручується в процесі деформації перекошуються (рис. 4).

 

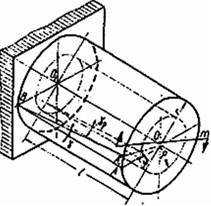
Рисунок 4 −Деформація бруса при скручуванні

Кут їх перекосу являє собою кут зсуву. Встановимо залежність між кутом зсуву і кутом закручування . З цією метою розглянемо трикутник АА1В на поверхні бруса. Завдяки малій величині дуги АА1 (нагадаємо, що в основу всього предмета опору матеріалів покладено принцип малості деформації) трикутник АА1В можна вважати плоским. Тоді  AA¹

tg=

AB

Оскільки для малих кутів 

tg = рад,

то

                                                                                  = AA1 .

                                                                           AB

З другого боку, як відомо з тригонометрії, 

 AA₁ = r,

де r- радіус бруса. Оскільки  AA₁  AA₁,то можна вважати, що  AA₁ = r.

Враховуючи це, одержимо

                                                            _{ = r}^,                                                  l тобто кут зсуву прямо пропорційний куту закручування.



                Відношення  являє собою кут закручування, що припадає на одиницю довжини

l

бруса. Називатимемо його відносним кутом закручування і позначимо літерою . При цьому вираз  = ^r набуває вигляду

l

 = r.

Виділяючи подумки із розглядуваного бруса циліндр довільного радіуса  і повторюючи ті самі міркування, одержимо

_ = .

З формули _ =  видно, що кут зсуву прямо пропорціональний відстані точки від центра перерізу і досягає найбільшого значення для точок, розміщених вздовж контуру перерізу, тобто при =r .

З припущення про незмінність відстаней між поперечними перерізами скручуваного бруса випливає рівність нулеві відносних поздовжніх деформацій , а отже, згідно з законом Гука (= E), і нормальних напруг . У поперечних перерізах бруса при деформації кручення виникають лише дотичні напруги їхня величина може бути знайдена з допомогою закону Гука для зсуву (= G):

_= G_= G_^.

            Найбільшої    напруги    зазнають    крайні    ділянки    поперечного     перерізу.

Максимальна дотична напруга

макс = Gr

Отже, дотичні напруги при крученні розподілені вздовж перерізу нерівномірно і в цьому істотна різниця між звичайним зсувом і крученням. Порівнюючи два останніх вирази приходимо до висновку, що

_ 

                                                                                                                  =     ,

                                                                                                      _max            r

тобто дотичні напруги прямо пропорціональні відстані точок від центра перерізу. Графічно розподіл дотичних напруг вздовж діаметра бруса подано на рис. 5, а. Такий графік називають епюрою дотичних напруг.

Як видно з епюри, точки, розміщені поблизу осі бруса, виявляються недонапруженими, основне навантаження припадає на шар матеріалу, що прилягає до поверхні бруса. Ця обставина і наводить на думку про створення порожнистих валів. Видаляючи матеріал поблизу осі валу (рис. 5, б), ми дуже мало знижуємо його міцність,

 

 

 

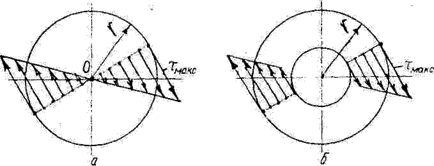
Рисунок 5 – Епюра дотичних напруг при крученні

 

оскільки ця частина матеріалу вала суцільного перерізу виявляється мало навантаженою, проте при цьому дістаємо значний виграш у вазі, що особливо важливо в літако- і ракетобудуванні.

Розглянемо, як визначається кут закручування . Дослідним шляхом встановлено, що величина цього кута залежить від прикладеного до бруса скручувального моменту, довжини бруса, його матеріалу, форми і розмірів поперечного перерізу. Найбільшого значення, як вже відмічалось, кут закручування досягає на вільному торці бруса. Його величину можна визначити за формулою

 

M^kl

                                                                                                      =  ,

GJ _p

де M _k −крутний момент (момент внутрішніх сил), який в розглядуваному

випадку дорівнює за величиною скручувальному моменту, прикладеному до бруса; l −довжина бруса;

G −модуль зсуву (модуль пружності другого роду);

Jp −полярний момент інерції – геометрична характеристика жорсткості перерізу при крученні (чим більша величина Jp, тим менший кут закручування бруса при інших однакових умовах).

Формула (6) подібна виразу закону Гука при розтягу (стиску) l = ^Nl , тому її EF іноді називають математичним виразом закону Гука при крученні. По аналогії з

           

 жорсткістю перерізу EF і жорсткістю бруса ^EFпри розтягу (стиску) запроваджують

l

GJ_

поняття жорсткості перерізу GJ_ і жорсткості бруса      при крученні. l

За формулою

макс = Gr

Значення можна знайти з вираз:

 

 M ^k

                                                                                                   =     =

                                                                                                             l      GJ_

Враховуючи це, для _максодержимо

                                                                                                       макс            Mkr

 =

J_

Поділимо чисельник і знаменник останньої рівності на r :

                                                                                                      макс               Mk       

 =

J_ :r

Відношення полярного момента інерції поперечного перерізу до його радіуса називають полярним моментом опору, або моментом опору крученню, і позначають     J

W^ =                                                                  r                                

Тепер формулу для найбільших дотичних напруг можна, представити так;

                                                                               M_k

                                                                   ^{ макс =}_W                                  

Звідси видно, що чим більший полярний момент опору Wртим менші дотичні напруги будуть виникати в поперечних перерізах бруса при одному й тому самому крутному моменті і тим міцнішим буде брус.

Тому кажуть, що полярний момент опору Wpє геометричною характеристикою міцності бруса при крученні.

 

Умова міцності при крученні. Умова жорсткості при крученні

 

Для забезпечення міцності бруса (вала) необхідно, щоб найбільші дотичні напруги _максне перевищували допустимої напруги при крученні [_к ], тобто 

                                                                                                  макс           Mk      k 

                                                                                                  =           

W_

Допустимі напруги при крученні звичайно беруть меншими, ніж при зсуві, оскільки кручення завжди в тій чи іншій мірі супроводжується вигином, який ми не враховували при виводі умови міцності. Для сталі _k  20120H / мм² .

Може статись, що вал, задовольняючи умову міцності, буде недостатньо жорстким, тобто буде пружинити, закручуючись на значний кут під дією скручувального моменту. Внаслідок цього такий вал буде передавати момент нерівномірно, що може призвести до виникнення небезпечних коливань.

           

Приймаючи певний допуск на точність виготовлюваної різі, обмежують кути закручування ходових гвинтів токарних верстатів. При великих кутах закручування значно змінюється крок різі. Чим вищою повинна бути точність нарізаної різі, тим менші кути закручування ходового гвинта можна допускати.

При великих кутах закручування валів механізмів пересування мостових кранів можливий навіть перекіс крана на рейках. Тому часто ставлять умову, щоб, крім міцності, вал мав достатню жорсткість, тобто щоб відносний кут закручування не перевищував деякої наперед заданої величини, тобто

                                                                                                           M^k            

= =  l GJ_

Допустимий відносний кут закручування встановлюється технічними умовами. Його величина для різних конструкцій і режимів роботи вала змінюється в досить широких межах. Залежно від призначення вала приймають

 

= (0,263,5)10⁻² рад/ м,

 

що приблизно відповідає

 

= 0,15 2,0 град/ м^.

 

Умова міцності:

 

                                                                                            ВСФ                                        ,

напруга = ГХП  _допустима напруга_

або Умова жорсткості:	M           макс = k  k . W
кут закручування = модуль або	ВСФ зсуву наполярний момент інерції	                                   доп.кут закруч.,                                  

                                                                                                         M^k            .

= =  l GJ_

Геометричні характеристики поперечного перерізу при крученні

 

Полярний момент інерції і полярний момент опору для круга і кільця. Умови міцності і жорсткості. Формули для визначення геометричних характеристик поперечних перерізів при крученні наведені в табл. 1. З цих формул видно, що полярний момент інерції має розмірність одиниці довжини в четвертому степені, а полярний момент опору – одиниці довжини в третьому степені.

Таблиця 1 − Формули для розрахунку полярного моменту інерції та полярного моменту опору

 

 

Три види задач при розрахунках на міцність при крученні

 

За умовою міцності (ф.9) можна вирішувати три види задач:

− перевірний;

− проектний;

− визначення допустимого навантаження.

І ПЕРЕВІРНИЙ – полягає у визначенні розрахункової напруги _{к max} = M_k /W_, MПа і порівняння отриманого значення з заданою допустимою напругою _k , MПа:

Якщо _{k max}  _k  - умова виконується, значить деталь (вал, оправка фреза, тощо) міцна;

Якщо _{k max}  _k  - умова не виконується, значить деталь не міцна.

ІІ ПРОЕКТНИЙ – найбільш поширений вид при проектуванні нових виробів, деталі яких можуть зазнавати кручення. Розміри поперечного перерізу деталі, наприклад діаметр d вала визначається шляхом перетворення ф.9:

Спочатку визначається W_Pіз умови міцності, а потім з урахуванням W_P  0.2d ³(табл. 1)знаходять діаметр d,мм:

 

M ^k ,

W_p 

_k 

або

 

                                                                                                                   M^k         .

d  3

0,2_k 

Розрахункове значення діаметра d необхідно закруглити до найближчого стандартного значення – числа парного або кратного «5»

III Визначення допустимого навантаження або допустимої передаваної потужності.

Цей вид задачі полягає у визначенні із умови міцності допустимого крутного  момента М_К , а потім допустимої потужності Р

 

M _k  W_p _k .

 

Знаючи співвідношення Р = М * із теоретичної механіки при заданому значенні кутової швидкості обертання вала , можна знайти допустиму потужність:

 

P M_k _.

 

Далі розглянемо кілька прикладів, в яких показано застосування різних розрахунків, а також внутрішньопредметних і міжпредметних зв’язків технічної механіки.

 

ПРИКЛАД 1

Сталевий валик діаметром d = 60мм і довжиною l=180мм, обточується різцем (рис 6). Визначити найбільші напруги кручення _К.МАХ і кут закручування валика, якщо зусилля різання F = 4800Н.с

 

 

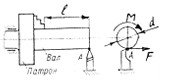
Рисунок 6 −До прикладу 1

 

Рішення

Значення _К.МАХ знайдемо за формулою:

К.МАХ = М К /WP Значення знайдемо за формулою:

                                                            = М_К *l/G*J_P

де Мк – крутний момент, який дорівнює за величиною скручу вальному, створюваному зусиллям різання:

М_К = F *d /2 = 4800*0.06 =144Нм W_P −полярний момент опору перерізу:

W_P = 0,2d ³ = 0.2*60³ = 43200мм³

J_P −полярний момент інерції перерізу: J_P = 0.1*d ⁴ = 0.1*60⁴ =1300000мм⁴

          

G – модуль зсуву, для сталі G=0,8*10⁵ Н / мм² Обчислення:

_К.МАХ =144000/43200=3,3Н / мм² =3,3МПа =144000*180/80000*13000000= 0,00025рад,

що відповідає приблизно 52

 

ПРИКЛАД 2.

Розточка циліндра двигуна виконується з допомогою стальної борштанги з поводком, на якому закріплюється різець. Визначити діаметр борштанги d і кут її закручування, якщо зусилля різання F=6800Н, діаметр циліндра D=540мм, довжина борштанги l=1400мм (рис 7).Допустима напруга на кручення для матеріалу борштанги _К=50МПаРішення

 

 

 

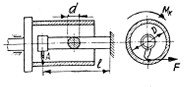
Рисунок 7 −До прикладу 2

 

 

Визначимо діаметр борштанги із умови міцності (II вид задач):  

 

M k ³  k ,

0,2d

 

                                                                                                                   M^k          .

d  3

0,2_k 

 

Кут закручування визначимо за формулою:

                                                     = М_К *l/G*J_P

Крутний момент Мк дорівнює скручувальному моменту, який створюється силою різання:

                                                                                    D                 540                  ⁴H  мм.

                                                                 Mk = F      = 6800         =18410

                                                                                    2                   2

Обчислення d:

18410⁴

d 3= 57мм.

0,250 Приймаємо стандартне значення d = 58 мм.

ПРИКЛАД 3

Виконати проектний розрахунок веденого вала одноступінчастого редуктора, якому передається потужність двигуна Р_дв = 4кВт, частота обертання вала двигуна 730об/хв, передаточне число редуктора u = 3,15, коефіцієнт корисної дії редуктора = 0,97, допустима напруга на кручення _к= 35 МПа.

 

 

 

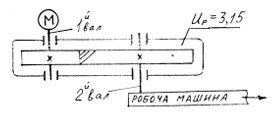
Рисунок 8 −До прикладу 3

 

Рішення 

Для розрахунків необхідно знайти крутний момент на веденому валу, який дорівнює обертовому моменту М₂: М_K2 = M₂.

 

М ₂ = М₁ *u_P *= 9.55P /n_двu_P_P .

 

Діаметр вихідного кінця веденого вала:

 

                                                                                                                   M^k          .

d  3

0,2_k 

Обчислення:

 

M2 =  =160Hм.

 

16010³

d 3= 28,3мм.

0,235

 

Призначимо діаметр вихідного кінця вала d = 28 мм.

Ведений вал редуктора має ступінчасту форму. Призначимо діаметри під стандартні підшипники кочення (діаметри шипів вала)кратні 5, тобто d_шип = 35мм, тоді діаметр головки вала (під колесом) d_коп = 40ммдіаметр упорного буртика d_бурт = 50^мм .

Контактні напруги

 

Працездатність багатьох деталей (зубів зубчастих коліс, підшипників, котків фрикційних передач, ланцюгів) визначається не загальною їх міцністю, а міцністю робочих поверхонь – тобто контактною міцністю.

Контактними називаються напруги, що виникають у зоні контакту двох деталей (стиск котків, натискання зубів, стиск шариків або роликів з кільцями підшипників).Позначаються контактні напруги _Н . По площині контакту _Н розподіляються нерівномірно – по еліптичному закону (рис 1).

 

 

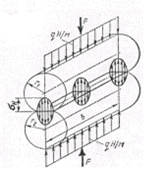
Рисунок 1 −Розподілення контактних напруг по еліптичному закону

 

Змінюються _Н по пульсуючому циклу напруг (рис 2).

 

 

Рисунок 2 −Пульсуючий цикл напруг

 

 

 

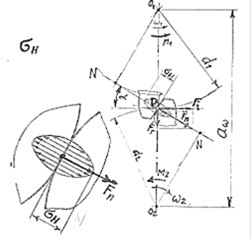
                                                 Рисунок 3 −  Контактні напруги між зубами зубчастих коліс Деформація −згин           

 

Згин – це деформація бруса, яка виникає під дією зовнішніх сил і пар сил, площина дії яких перпендикулярна до поздовжньої осі бруса Z. Брус, який згинається під дією зовнішніх навантажень в інженерних розрахунках називають балкою. Приклади виробів, які відносяться до так званих балок (вони мають велику довжину при невеликій товщині і можуть прогинатись під дією зовнішніх сил):

− шини в електромережах, закріплені в опорних запобіжниках вигинаються при протіканні в них ударного струму короткого замикання;

− опори повітряних ліній електропередач;

− вал електродвигуна у місці закріплення якоря;

− оправки і зубці фрез;

− зубці протяжок;

− зубці зубчастих коліс;

− вали циліндричних, конічних і черв’ячних редукторів;

− осі залізничних і трамвайних вагонів;

− різці у токарному верстаті; − ділянки мостів між опорами.

При згині балки її поздовжня вісь Z викривляється, а шари волокон розтягуються, стискаються або залишаються без зміни – залежно від їх розташування відносно осі Z і напряму дії зовнішньої сили F (рис. 1).

 

 

 

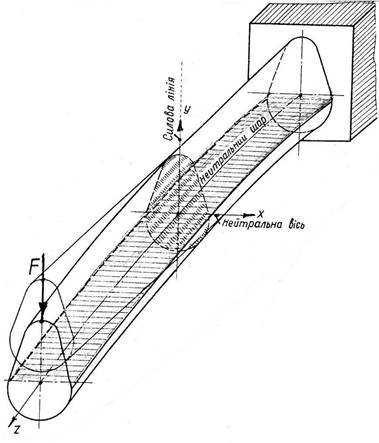
Рисунок 1 – Деформації шарів поздовжніх волокон балки при згині

У відповідність із деформаціями поздовжніх шарів волокон в поперечних перерізах балки виникають нормальні напруги розтягу _pі стиску c, які розподіляються нерівномірно по висоті поперечного перерізу балки (доведено математично) – лінійному закону (рис. 2).

 

 

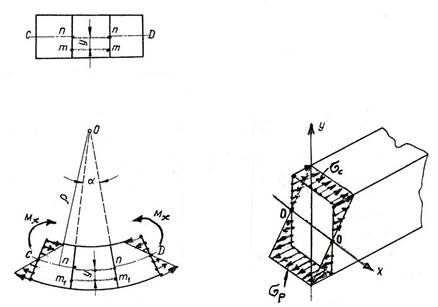
Рисунок 2 – Нерівномірний розподіл нормальних напруг pта cпри згині балки

 

При розрахунках названих вище виробів на міцність при згині необхідно знати величину найбільшої фактичної напруги maxв небезпечному перерізі балки (так називають розрахункову схему будь-якого виробу). Величина maxзалежить від багатьох факторів:

− спосіб закріплення кінців балки (дві шарнірні опори чи жорстке затиснення одного кінця консольної балки – це було розглянуто в теоретичній механіці);

− місця і напрям прикладених зовнішніх сил F₁, F₂і моментів М₁, М₂до балки; − величин (числових значень) сил і моментів;

− форми і розмірів поперечного перерізу балки (круг, квадрат, кільце, прямокутник, двотавр, швелер і т. ін.).

Названі фактори представлені в основній розрахунковій формулі, яка має назву – умова міцності при згині:

M

                                                                                                               xmax     зг,

                                                                                          max = W              

x

де max −найбільша розрахункова (або фактична) напруга в небезпечному перерізі

балки;

^Mx_max − найбільше числове значення згинального моменту, яке визначається після розрахунків на основі методу перерізів;

^W_x − осьовий момент опору поперечного перерізу балки, залежить від форми і розмірів перерізу балки;

_зг − допустима напруга, величина якої залежить від матеріалу балки (сталь, чавун, деревина тощо) і вимог до даної конструкції чи деталі, ця величина в умовах задач задається.

Цей вираз (нерівність) називається “умовою міцності” тому що:

− якщо розрахункова напруга maxв розрахунковій деталі не перевищує заданої допустимої напруги _зг −тобто max __зг, це є гарантією міцності деталі в заданих умовах її роботи;

− якщо ж виходить нерівність виду max __зг- деталь не міцна: в такому випадку треба зменшити величину зовнішніх навантажень, або збільшувати товщину деталі, або замінити матеріал балки на більш міцний, якщо така заміна можлива – з метою забезпечення умови міцності max __згі надійної експлуатації даного виробу.

Метод перевірки – так називають метод визначення величин згинальних моментів

M_xв перерізах біля кожної характерної точки по довжині балки. Позначення M_x відповідає прогину балки у вертикальній площині YZ, коли поздовжня вісь Z балки начебто утворює дугу відносно осі Х поперечного перерізу балки. (При згині балки в горизонтальній площині ХZ згинальний момент позначається ^M_y).

^M_x −це один із шести внутрішніх силових факторів (ВСФ) в поперечному перерізу бруса. При спрощених розрахункових схемах балки його величину біля кожної точки на балці визначати за формулою:

 

Mx =Mточки(Fi ) ,

 

тобто  згинальний момент дорівнює алгебраїчній сумі моментів від зовнішніх сил і пар сил, прикладених до залишеної частини балки (лівої від проведеного перерізу чи правої) відносно точки, біля якої проведений переріз (рис. 3). Момент ^M_xзрівноважує дію моментів від зовнішніх сил. Розглянемо приклад визначення величини ^M_xзгідно рис. 3 для зображеної консольної балки: в цьому прикладі правило знаків моментів зовнішніх сил не відрізняється від правила, прийнятого раніше в задачах статики. Величини M_xвизначається послідовно зліва направо; біля точки D, в якій прикладений заданий момент М, згинальний елемент ^M_xвизначається два рази – ліворуч від неї і праворуч.

 

 

 

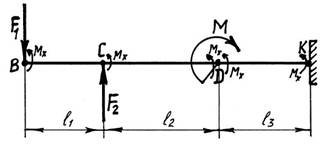
Рисунок 3 −Визначення згинальних моментів М_х біля характерних точок балки

Примітка: при визначені згинальних моментів ^M_x біля характерних точок балки в напрямі справа наліво додатними моментами є моменти сил і пар сил проти годинникової стрілки (тобто для правої ділянки балки правило знаків зовнішніх моментів змінюється на обернене) (рис. 5).

Правило знаків для згинальних моментів ^M_xможна пов’язати з характером деформації балки: ^M_xвважають додатним (рис. 4), якщо балка згинається зовнішніми силами  опуклістю донизу; ^M_xвважають від’ємним – при вигині балки догори (рис. 4). Отже, при додатному ^M_xрозтягнуті волокна балки розміщуються внизу, а при від’ємному – вгорі (це зручно запам’ятати як «правило зонта» або «правило дощу» −  вода збирається −  +^M_x , вода виливається - –^M_x .

 

 

 

Рисунок 4 – Правило знаків згинальних моментів ^M_xпов’язане з деформаціями поздовжніх волокон балки

 

 

 

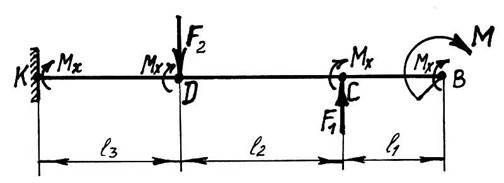
Рисунок 5 – Визначення згинальних моментів ^M_xдля правої консольної балки справа наліво

 

Біля точки В − М_х = −М;

Біля точки С − М_х = −М;

Біля точки D − М_х = −М+F₁l₂;

Біля точки К − М_х = −М+F₁(l₂+l₃)−F₂ l₃.

Епюри згинальних моментів

 

Для наочності і для перевірки правильності розрахунків згинальних моментів

^M_x прийнято будувати графіки зміни згинального моменту вздовж осі балки – такі графіки називають епюрою M_x . Епюри будують в проекції під розрахунковою схемою балки, в масштабі; додатні величини ^M_xвідкладають вгору від осі епюри, від’ємні ^M_x − вниз. Вісь епюри – базова лінія, паралельна поздовжній осі балки Z. Розглянемо кілька прикладів розрахунків згинальних моментів M_x , побудови  в небезпечному перерізі балки.

 для зображення консольної балки. (рис. 6)

Точка В    Mx = 0;

Точка С    Mx = − F l ; ^M_xmax= F l .

Небезпечний переріз співпадає із затисненням консольної балки.

 

 

 

Рисунок 6 – Епюра ^M_xдля зображеної консольної балки до прикладу 1

 

 

Приклад 2. Визначити ^M_xmax для зображеної балки на двох шарнірних опорах

(рис. 7)

F

                                                                                                Реакції         Y_A =Y_B =  ;

2

Точка А       M_x = 0;

Точка С       ^M_x =Y_A  ₂^l = ^F₄^l ;

Точка В       ^M_x =Y_A l − F  2^l = ^F2 l − F  2^l = 0 .

Небезпечний переріз балки знаходиться посередині біля точки С; 

Mxmax= F l

4

 

 

Рисунок 7 – Епюра ^M_xдля зображеної балки на двох опорах до прикладу 2

 для зображеної консольної балки (рис. 8).

 

 

 

 

F₁ = 40 кН;

F₂ = 90 кН;

М = 80 кН  м;

l₁= 0,5 м; l₂ = 0,7 м; l ₃ = 0,8 м.

 зображеної балки до прикладу 3

 

Точка В                  ^M_x =0;

Точка С ліворуч        Mx =F1 l1;

Точка Справоруч      Mx =F1 l1 − M ;

Точка D                  ^M_x =F₁ (l₁ +l₂)− M ;

Точка К                  ^M_x =F₁ (l₁ +l₂ +l₃ ) − M − F₂ l₃ .

 

Обчислення величин ^M_x , кН  мдо прикладу 3:

Точка В                  ^M_x =0;

Точка С _{ліворуч}        ^M_x =400,5 = 20;

Точка С_{праворуч}      ^M_x =400,5−80 = −60 ;

Точка D                  ^M_x =401,2 −80 = −32;

Точка К                  ^M_x =402 −80−900,8 = −72.

Небезпечний переріз балки знаходиться біля точки К в затисненні балки, тому що під точкою К на епюрі M_xвеличина ^M_xmax = 72 кН  м.

Примітка: для прискорення розрахунків і перевірки правильності побудованої епюри згинальних моментів ^M_xдоречно знати такі правила:

− біля точки на кінці балки, в які прикладена тільки задана сила F, або реакції опор Y_Aабо Y_B–  ^M_x = 0 завжди;

− біля точки на кінці балки, в якій прикладений тільки заданий момент М – ^M_xдорівнює цьому моменту з відповідним знаком: ^M_x = М, або ^M_x = – М; 

− біля проміжної точки, в якій прикладений заданий момент М, величину ^M_xтреба визначити двічі – до точки і після неї. На епюрі ^M_xпід цією точкою буде стрибок на величину заданого моменту;

− під проміжною точкою, в якій до балки прикладена задана сила F, на епюрі буде злом лінії епюри, тобто зміна кута нахилу відрізка прямої;

           

− обрив епюри ^M_xмає форму складної ломаної лінії із відрізків прямих, похилих до осі епюри;

− під консольною ділянкою балки, до якої прикладений тільки заданий момент М – на епюрі ^M_x буде відрізок прямої, паралельний осі епюри Х.

 

Осьові моменти опору перерізу при згині

 

Осьовий момент опору перерізу при згині ^W_x(або ^W_y ) залежить від форми і розмірів поперечного перерізу балки, а також від розташування перерізу відносно навантаження. Без доведення приведемо кілька формул для найбільш поширених перерізів балок у формі круга, квадрата, прямокутника, двотавра. (рис. 9). Одиниці вимірювання W_x– м³, см³ , мм³:

− переріз балки – круг: W_x = W_y =^d3 ;

32

− переріз балки – квадрат: W_x = ^W_y = ^a3 ;

6

− переріз балки – прямокутник, повернутий ребром відносно навантаження:

bh²

W_x=  ;

6

− переріз балки – прямокутник, повернутий ребром відносно навантаження:

Wy = b2 h ; 6

− балка виготовлена із стандартного металопрокату, наприклад двотавра. Величини ^W_xта ^W_y , см³ знаходяться за таблицями сортаменту згідно номеру профіля: ^W_xвибирається, якщо згідно умові двотавр знаходиться в нормальному положенні, а ^W_y −коли двотаврова балка повернута плазом відносно навантаження.

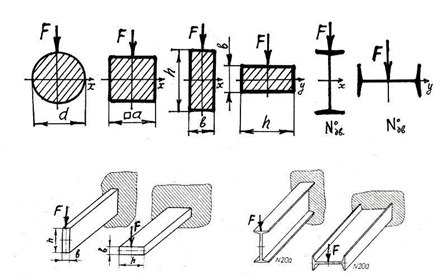
Рисунок 9 – Типові форми поперечних перерізів балок та їх розташування відносно навантаження

Три види задач при розрахунках на міцність при згині

 

На основі формули – умови міцності при згині можна вирішувати три види задач: перевірний розрахунок, проектний розрахунок, визначення допустимого навантаження.

Перевірний розрахунок полягає у перевірці міцності балки, про яку все відомо:

− ^M_xmax −із побудованої епюри ^M_x , кН  м;

− ^W_x − визначений згідно заданій формі і розмірам перерізу балки, мм³;

− _зг −задана з урахуванням матеріалу балки і вимоги до її надійності, МПа.

Необхідно обчислити величину максимальної розрахункової напруги в небезпечному перерізі балки _згза формулою:

Mxmax

_згmax =, та порівняти отримане значення _зг , МПа із заданою W_x

допустимою напругою, скласти відповідний висновок:

− якщо _згmax  _зг- балка міцна;

− якщо _згmax  _зг- балка не міцна.

Проектний розрахунок полягає у визначенні необхідних розмірів поперечного перерізу балки, які здатні забезпечити міцність балки. Для цього спочатку треба визначити геометричну характеристику перерізу W_x , а вже потім розміри, наприклад: діаметр круглого перерізу d, розміри квадратного перерізу aa , розміри прямокутного перерізу b та h, номер двотавра або швелера. Величина ^W_xвизначається із умови міцності при згині: 

Mxmax . ^W_x 

_зг

Діаметр круглого перерізу визначається із формули ^W_x =d3  0,1d3так: 32

d  3 32Wx = 3 Wx = 3 10Wx ;

                                                                                                          0,1

a3

                 Розмір квадратного перерізу визначається із формули ^W_x = так:

6

 

a  ³ 6^W_x .

 

Визначені розміри d, a, b, h, мм треба закруглити до найближчого більшого стандартного числа, кратного 2 або 5, мм.

Номер двотавра або швелера визначається так: в таблиці сортаменту знаходиться найближче більше значення ^W_x , см³у порівнянні з розрахованою величиною ^W_x , см³ − і уточнюється, якому номеру профілю ця величина відповідає.

Приклади розрахунків балок на міцність при згині розглядаються на практичних заняттях і при підготовці до виконання розрахунково-графічної роботи.

Раціональні перерізи балок при згині

 

Осьовий момент опору є геометричною характеристикою балки при згині, тому необхідно прагнути до того, щоб при одній і тій же витраті матеріалу він був найбільшим. Але при заданій довжині балки витрата матеріалу (вага балки) прямо

W^xдля пропорційна площі поперечного перерізу А. Отже, чим більше відношення

A обраного перерізу балки, тим раціональнішою є його форма. Тому дане відношення і треба вважати мірою раціональності поперечного перерізу при згині балки із пластичного матеріалу.

Найбільш раціональною формою перерізу балок при згині є двотавр, тому що згідно епюрі нормальних напруг _згв поперечному перерізі балки найбільші напруги

maxвиникають на поверхневих шарах волокон – тому з найбільшою віддачею працює матеріал, який співпадає з наличками двотавра (рис. 10). Весь об’єм матеріалу, який виходить за межі двотаврового профілю в порівнянні з іншими (круглим, квадратним, прямокутним) – дуже мало працює на міцність балки, а щільну збільшує її загальну масу (тобто вагу) і витрати матеріалу (рис. 10).

 

Рисунок 10 – Порівняння розподілу матеріалу по поперечних перерізах балок при згині

 

Представимо у формі таблиці витрату матеріалу на балки з різними поперечними перерізами при їх однаковій міцності – тобто для всіх шести прикладів ^W_x = 81,7 см³для двотавра №12, а площа перерізу А = 17,4 см² .

 

Таблиця 1 −Витрати матеріалу на балки різних поперечних перерізів

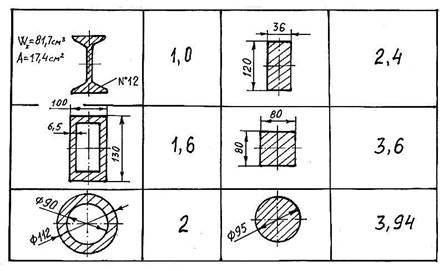
Міцність балки залежить не лише від форми і розмірів її поперечного перерізу, але й від положення перерізу відносно діючого навантаження. Наприклад, балка прямокутного перерізу з відношенням сторін hb = 3здатна витримати втричі більше навантаження, якщо вона повернута ребром, а не плазом. Для двотавра №20, а це співвідношення дорівнює 7,2 рази, тому що  Wx = 203 = 7,2.

                                                                                               W_y        28,2

 

Приклад 4

Зуб протяжки (рис. 11) працює на згин. Сила різання F = 132 кН. В процесі протягування одночасно беруть участь п’ять зубців протяжки. Визначити ширину h зуба в небезпечному перерізі, якщо висота зуба l = 6 мм, а товщина b = 12 мм. Допустима напруга на згин для швидкорізальної сталі σ_зг= 310 МПа.

 

 

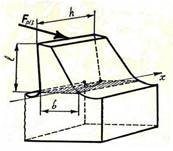
Рисунок 11 −Розрахункова схема зуба протяжки

 

Розв’язування

На кожний зуб протяжки діє сила 

F₁= F/5;

F₁= 13210³/5 = 26400 Н. Зуб протяжки розглядається як консольна балка, навантажена силою F (дивись рис. 6). Найбільший згинальний момент виникає біля ніжки зуба:  M xmax= F1 l;

M _xmax= 264000,06 =1584Hм.

Осьовий момент опору перерізу із умови міцності при згині:

 

M xmax ;

W_x 

_зг 

W_x  158410³ = 510мм₃.

310

Для прямокутника

b² h

                                                                                                    W_x  .

6

Необхідну ширину зуба обчислимо із формули h  6bW2 x ;

h   = 21,3мм.

Призначаємо стандартне значення h = 22 мм.

Поняття про розрахунки на жорсткість при згині

 

Працюючі на згин елементи будівельних та машинобудівних конструкцій в багатьох випадках повинні бути розраховані не тільки на міцність, але і на жорсткість. При цьому часто виявляється, що необхідні розміри поперечного перерізу балки повинні бути визначені із умови міцності на жорсткість.

Під дією зовнішніх навантажень поздовжня вісь балки викривляється. Зігнута вісь балки є плавною кривою лінією (рис. 12), її називають пружною лінією балки. У випадку прямого згину площина прогину балки співпадає з площиною дії зовнішніх сил.

Величина прогину y і кут повороту поперечного перерізу балки залежать від таких факторів:

− довжина балки, l;

− навантаження F, M, q − їх величини та місця прикладання до балки;

− матеріалу балки − модуль пружності матеріалу Е;

− форми поперечного перерізу балки: круг, кільце, прямокутник, квадрат, двотавр −момент інерції перерізу Jx;

− розміри перерізу d, D, d₀, b, h, a, №;

− розташування поперечного перерізу балки відносно діючих сил (ребром чи плазом) −момент інерції перерізу Jx, або Jy;

− способів закріплення кінців балки: шарнірні опори, або жорстке затиснення одного кінця консольної балки (числові коефіцієнти).

Ці фактори входять до складу формул при розрахунках переміщень y і . Найбільший прогин ymax позначається f і називається стрілою прогину балки (рис. 12).

Крім розрахунків на міцність за умовою _згmax _згвідповідальні деталі часто перевіряють на жорсткість: стріла прогину f і кут maxне повинні перевищувати допустимих величин:

                                                                               y_max = f  f ;     _max  ,

де f − у міліметрах;  −в радіанах.

В залежності від призначення деталей і вимог до них призначають такі допустимі величини:

                                                               f =^_ ¹ ...   ^{1 }_l;     0,001рад.

                                                                              200   1000

При розрахунках конструкцій на жорсткість при згині трапляється такі ж три види задач, що і при розрахунках на міцність: перевірні, проектні та визначення допустимого навантаження. Розміри поперечного перерізу балки, визначені із умови міцності та із умови жорсткості відрізняються. Для виготовлення балки визначають більші розміри із двох обчислених.

Значення величин f і можна визначити за допомогою вимірювальних приладів на спеціальному лабораторному обладнанні.

           

 

 

 

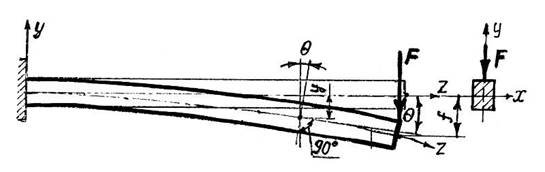
Рисунок 12 − Пружна лінія балки, стріла прогину балки, кут повороту поперечного перерізу балки

 

 

Таблиця 2 −Розрахункові формули для обчислення стріли прогину балки і кута

повороту поперечних перерізів для кількох простих схем балок

    

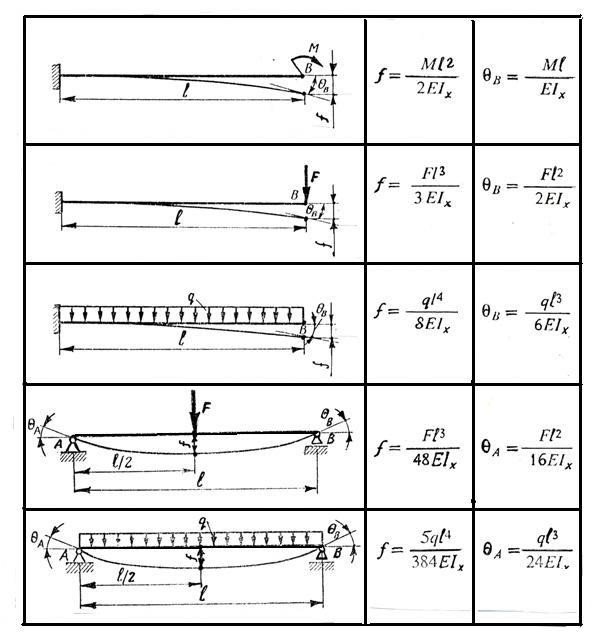
Список літератури

 

1        Ердеді О. О. та ін. Технічна механіка. −К.: Вища школа, 1983. − 368 с.

2        Аркуша А. И. и др. Техническая механіка. – М.: Высшая школа,  1983 – 447 с. 3 Мовнин М. С. и др. Основы технической механики. – Л.: Машиностроение, 1982. – 288 с.

4        Ицкович Г. М. Сопротивление материалов. – М.: Высшая школа, 1986. – 352 с.

5        Эрдеди А. А. и др. Техническая механика. – М.: Высшая школа, 1991. – 304 с. 6 Писаренко Г. С. та ін. Опір матеріалів: підручник – 2-ге вид; допов. і переробл.

− К.: Вища шк.; 2004.- 655 с.

7   Ярмицький А. Г. Опір матеріалів. − К.: Техніка, 1968.- 128 с.

8   Дубейковский Е. Н. Сопротивление материалов. −Учеб. пособ. для машиностроит. спец. техникумов.- М.: Высшая школа, 1985. −192 с.

           

Додлаток А

(довідковий)