Текст " ПРИКЛАДНА СПРЯМОВАНІСТЬ ВИКЛАДАННЯ МАТЕМАТИКИ"

Про матеріал

Робота присвячена прикладнійспрямованості викладання математики. Вона містить цікавий і корисний матеріал, десистематизовані знахідки та розробки матеріалів для вчителів, нестандартні уроки, лабораторні роботи з математики та креслення у школі.

Перегляд файлу

Управління освіти адміністрації Основянського району

Харківської міської ради

Харківська вечірня ( змінна ) школа №3

Харківської міської ради Харківської області

ПРИКЛАДНА СПРЯМОВАНІСТЬ

ВИКЛАДАННЯ МАТЕМАТИКИ

Харків

Рекомендовано методичною радою управління освіти адміністрації

Червонозаводського районуХарківської міської ради

Рецензенти: Надточій О.І.,завідувач РМЦ управління освіти адміністрації Червонозаводського району.

Автор-укладач: Каліта Емма Євгеніївна, вчитель математики ХВ(З)Ш №3, кваліфікаційна категорія «спеціаліст першої категорії».

Прикладна спрямованість викладання математики,– 25с.

Зміст

1.	Вступ………………………………………………………………………
2.	Використання прикладної спрямованості математики. Педагогічні функції прикладних задач ………………………………………………
2.1.	Задачі з виробничим змістом при вивченні показникової функції. Прикладні задачі з математики на будівництві…………………….…
2.1.1.	Алгебра, геометрія та прикладні задачі. Прикладні задачі при будуванні власної оселі…………………………………………………
2.1.2.	Похідна та її застосування при розв’язанні прикладних задач……….
3.	Креслення, як графічна підготовка учнів до життя……………………
4.	Лабораторно – графічні роботи…………………………………………
5.	Висновок…………………………………………………………………
6.	Список використаних джерел…………………………………………...

Вступ

Одна з важливих задач сучасної школи є надання учням глибоких та твердих знань з основ наук, виховання в них прагнення до неперервного удосконалення своїх знань та вмінь, самостійно поповнювати їх та використовувати на практиці.

Важливою умовою в удосконаленні викладання є посилення політехнічної спрямованості, яка повинна здійснюватися при вивченні усіх без винятків дисциплін середньої школи.

На уроках математики разом з вивченням теоретичного матеріалу учні повинні вміти виконувати виміри та розв’язувати задачі з виробничо-технічним змістом; користуватися довідниками та таблицями, простішими пристроями, виконувати різні господарські розрахунки, будувати схеми, діаграми і графіки, вільно володіти інструментами для креслення та вимірів, тощо.

В першій частині роботи перелічені деякі функції, які використовуються у математиці, фізиці, астрономії.

Друга частина має приклади задач, які використовуються на будівництві.

Третя частина присвячена кресленню, як частині виховання навичок виконання геометричних малюнків, вміння уявляти стереометричні фігури з різних позицій та композицій та пропедевтиці підготовки майбутніх студентів до навчання у вищих технічних закладах.

У четвертій частині наведені приклади математичних лабораторних робіт, які сприяють зацікавленості учнів своєю відмінністю від звичайних робіт, пошуково-дослідницькою діяльністю, можливістю виконувати ці роботи у групах та при різних рівнях підготовки учнів.

Використання прикладної спрямованості математики.

Педагогічні функції прикладних задач

Серед напрямків, які можуть поліпшити рівень і якість шкільної математичної освіти, є підсилення її практичного і прикладного спрямування. Практичне спрямування шкільного курсу математики передбачає вироблення в учнів умінь використовувати здобуті знання під час вивчення як самої математики, так і інших навчальних предметів, при цьому застосувати раціональні обчислювальні прийоми; користуватися обчислювальною технікою.

Прикладні задачі сприяють виконанню багатьох завдань навчального процесу. Крім безпосередньої підготовки учнів до свідомого дослідження реальних явищ природи, ці задачі дають можливість розкривати методологічні питання взаємозв’язку теорії з практикою під час вивчення математики та формувати в учнів наукове світорозуміння. За їх допомогою вчителі можуть активізувати пізнавальну діяльність учнів, підвищити їх інтерес до навчального предмета. Важливим фактором формування наукового світорозуміння є те, що математичні формули, теореми, різні залежності створюються під впливом практики і практичних потреб людини.Найбільш ефективним засобом навчання є міжпредметні пізнавальні задачі, для розв’язання яких треба залучення знань із декількох предметів.

Такі задачі сприяють росту самостійності учнів у здійсненні (впровадженні) міжпредметних зв’язків, вмінню узагальнювати знання з різних предметівпри вивченні загальних об’єктів і питань. Міжпредметні задачі можуть бути цілеспрямовані на досягнення пізнавальної мети. Під час розв’язування таких задач учні не тільки навчаються застосовувати математичні знання, а й дістають деякі нові відомості. Одночасно учні набувають корисних навичок роботи з довідниками, навчаються самостійно знаходити потрібну інформацію в довідниковій літературі.

Вивчення розділу «Елементарні функції» дає можливість підвести учнів до усвідомлення того, що кожна функція математично формулює залежності між реальними величинами різних явищ, причому та сама функція застосовується для опису явищ і процесів.

Приклади :

1.Функція y = k x:

1) залежність між шляхом S, пройденим тілом при сталій швидкості V і часом t його руху: S = Vt;

2) між вартістю P купленого товару, його кількістю K і сталою ціною t: P = Kt;

3) між довжиною кола C і його діаметром d: C = πd;

4) між потужністю струму Р і його силою І при сталій напрузі U: P = IU;

5) закон Ома: U = RI;

6) рівняння конденсатора: q = CU;

7) залежність тиску ідеального газу від кінетичної енергії руху молекул:

p = 2/3 _*nE

8) залежність кінетичної енергії молекул від температури: E = 3/2 _*kT;

9) залежність маси від кількості речовини: m = Mv.

2.Функція y = ax²:

1) закон вільного падіння тіла: S =1/2 _*gt²;

2) залежність енергії Е рухомого тіла при сталій масі m від його швидкості v(кінетична енергія): E = ½ _*mv²;

3) залежність між шляхом S при рівноприскореному русі від t, коли v₀=0

S = (at²)/2;

4) залежність кількості тепла Q, що виділяється струмом за певний проміжок часу, від сили струму I , опору провідника R , часу проходження струму t:

Q = I²Rt.

3.Функція y = a_*x²+ b_*x+c:

1) залежність між шляхом S при рівноприскореному русі від часу t :

S = v_ot + (at²) / 2;

2) висота h, на якій кинуте вертикально вгору тіло буде знаходитися через час t, де v_o - початкова швидкість, g - прискорення вільного падіння:

h = v_ot – (gt²) / 2.

4.Пряма пропорційність y = kx:

1) ізохорний процес: P₁/T₁=P₂/T₂

2) ізобарний процес: V₁/T₁=V₂/T₂

3) теплове розширення тіл l=l_o(1+at)- лінійна функція;

4) залежність питомого електричного опору металів від температури

ρ = ρ_o(1+at) -лінійна функція.

5.Обернена пропорційність y = k/x:

1) ізотермічний процес: P₁V₁=P₂V₂

2) рух рідини по трубах: s₁t₁ =s₂t₂

3) формула для обчислення відстані до зірки, де π^ІІ- її паралакс у кутових секундах R= k / π^ІІ

6.Логарифмічна функція:

1) формула Ціолковського: v- швидкість ракети, m - її масa v = v_rlnm_o/m;

2) коефіцієнт звукоізоляції D =A lg p_o/p.

7.Показниковафункція:

1) закон радіоактивного розпаду N=N_o 2^-1/^T;

2) зріст народонаселення N=N_oе^at;

3) барометрична формула p=p_oe^-^kh^/^H.

Задачі з виробничим змістом

при вивченні показникової функції

Під час вивчення теми «Показникова функція» за допомогою формули D=0,4+0,3_*2^k вдалося визначити відстань планет Сонячної системи від Сонця, якщо замість k підставляти відповідно 1,2,3,4,5… Ця формула допомогла вченим визначити положення трьох найвіддаленіших планет, які в телескопі були малопомітні.

Прикладні задачі з математики на будівництві

Під час вивчення теми «Показникова функція» за допомогою формули t_T= a^T ( t_o– t_н) + t_н(t_o- температура бетонній суміші під час завантаження до автозмішувача; t_н – температура повітря; T– час в хвилинах під час якого температура суміші дорівнюватиме t_T; а – постійний коефіцієнт, який залежіть від характеристик автомашини ) учні мають можливість ознайомитися із законом застигання бетонній суміші при транспортуванні бетону у автобетонозмішувачах.

1.За 10 хвилин після завантаження бетонної суміші до авто бетонозмішувача температура суміші знизилася з 38⁰до 35,7⁰при температурі повітря – 22⁰. Визначити, яка буде температура суміші через годину після загрузки?

До формули t_T= a^T ( t_o– t_н) + t_нтреба підставити дані з умови, після чого отримуємо: а¹⁰=0,962, звідки знаходимо а²⁰=0,792. Скористаємося знову формулою t_T= a^T ( t_o– t_н) + t_н визначаємо t₆₀=25,5⁰.

2.Яка повинна бути початкова температура бетонної суміші, щоб при температурі повітря – 25⁰ на будівництво підвозили бетонну суміш з температурою не нижче +30⁰ , якщо на перевезення витрачається 50 хвилин. Транспортування суміші відбувається авто бетонозмішувачами, для яких коефіцієнт а=0,997.

З формули t_T= a^T ( t_o– t_н) + t_н здобуваємо t_o= t_н+ ( t_T- t_н) / a^T, звідси t_o=+39⁰.

3.Визначити годинникову витрату тепла на обігрівання жилого будинку, розміри якого в плані 33,6*12 (м), висота 12 м, t_в=17⁰t_н= - 37⁰.

Кількість тепла Q ккал/ч, яке втрачається огорожею будови за одну годину, визначається формулою: Q= kS( t_в -t_н), k – коефіцієнт теплопередачі огорожі ккал/ч_*м²_*град, S – поверхня огорожі в м², t_в – температура повітря у приміщенні, t_н - розрахункова зимова температура повітря на вулиці в град. Найбільший годинникова витрата тепла Q на обігрів житлових та культурно-побутових будов виражає формула Q = (V^0,833(t_в -t_н)) / (0,33 – 0,01 t_н), де V - розміри будови по зовнішньому обміру в м³, t_в – розрахункова температура повітря у приміщенні, t_н - розрахункова зимова температура повітря на вулиці. Безпосередньо підстановкою до формули даних задачі знаходимо Q=92000 ккал. Ця задача вирішується за допомогою таблиць логарифмів. Постановка питання та засобів розв’язування цих задач відповідають тому, з чим ми зустрічаємося у житті. До розв’язування задач повинна бути попередня підготовча робота, мета якої навчити учнів користуватися довідниками, вибирати необхідні дані.

4. Визначити, скільки секцій радіаторів необхідно встановити у квартирі крупно панельного будинку, стіни якого мають товщину 250 мм, якщо квартира має одну зовнішню стіну довжиною 8,4 м та висотою 2,7 м. Квартира має 3 вікна розміром 1,5*1,5 м, балконі двері 0,8 *2,3м. Одна секція радіатора може дати в годину до 130 ккал тепла, t_в=18⁰_,t_н= - 37⁰.

Дані для розв’язування задач учні мають взяти з таблиці:

Конструкція огорожі

Товщина огорожі

Коефіцієнт теплообміну

в ккал/ч*м²_*град

Стіни з червоної цегли товщиною у 2 цегли

у 2,5 цегли

525

655

1,07

0,90

Стіни з великого шлакобетонних блоків (уд.вага 1500 кг/м³)

400

500

600

1,19

0,99

0,85

Стіни з великого коміркового бетону (уд.вага 800 кг/м³)

250

300

350

0,91

0,77

0,67

Перекриття на горищі по залізобетонному багатопустотному настилу (220 мм) утепленні шлаком. При товщині шлаку

100мм

200 мм

300 мм

320

420

520

1,11

0,74

0,55

Вікна дерев’янні із подвійними переплетами

---

2,33

Двері зовнішні: одинарні

подвійні

---

4,00

2,00

Підлоги над холодними підвалами

---

0,52

Визначивши площу огорожі будинку, використавши дані з таблиці, можемо знайти загальні тепловтрати: 2,33_*6,75_*(18+37) = 65(ккал/ч),0,91_*14,09_*(18+37)= =705 (ккал/ч/). Вони дорівнюють1773 ккал/ч/тоді кількість секцій радіаторів буде близько 14: 1773:130 13,6 (шт.). Після розв’язування цієї задачі учні мають можливість підрахувати кількість секцій радіаторів у їх класній кімнаті. Для цього вони повинні будуть безпосередньо зробити виміри розмірів усіх зовнішніх огорож та, користуючись даними таблиці, зробити підрахунки.

Алгебра, геометрія та прикладні задачі

При вивченні геометрії необхідно показати учням використання різних геометричних форм у архітектурі, так як архітектурні будівлі мають прості геометричні форми та їх композиції, одягнуті у дерево, камінь, метал, залізобетон, скло та пластмасу: чотири кутові піраміди древнього Єгипту, обрамлений колонами паралелепіпед афінського Парфенону, еліптичний циліндр римського Колізею, увінчаний півкулею круговий циліндр римського Пантеону та інші пам’ятники архітектури вражають різними формами. Використання на уроках математики картин із зображенням кращих пам’ятників архітектури сприяє глибшому розумінню математики, її ролі в архітектурі, розвиває естетичні смаки, сприяє інтересу до архітектури і будівництву, повагу до людини праці, які створили такі будівлі.

При введенні нових понять та аксіом слід завжди звертати увагу до предметів і явищ зовнішнього світу, ставити запитання, які допоможуть вирішити життєві проблеми, як то: « для виявлення нерівностей шпаклівки будівельники користуються довгою рейкою - «правилом», прикладаючи яку до поверхні, яку шпаклювали, впевнюються, що на ній немає зазорів понад можливі. Яку властивість площини використовують будівельники при перевірці якості шпаклівки за допомогою правила?».

Прикладні задачі прибудуванні власної оселі

При вивчені розділів про взаємне розташування прямих і площин у просторі, а також двогранні та многогранні кути в якості наглядного посібника корисно використовувати креслення, а ще краще моделі двоскатної або чотирискатної покрівлі.

Лінійний кут двогранного кута можна ввести, використовуючи креслення або моделі двоскатної покрівлі. Враховуючи, що найменшій уклін скатів для покрівлі з черепиці – 27⁰, для покрівлі з листової сталі, шиферу та азбестового листа – 16⁰, для покрівель з рулонних матеріалів – 6⁰. Раціональний вибір уклінну ската має більше значення для пониження вартості покрівлі. Круті покрівлі потребують більших витрат матеріалів. Корисно також розглянути розв’язок задач на підрахунки елементів покрівель будівель, елементів сходів та інше.

5. Запропоновані два проекти чотирискатної покрівлі для будинку розміром в плані 42*12 м. За першим проектом кут нахилу площини скату покрівлі до горизонту дорівнює 25⁰, по второчу 35⁰. Визначити, за яким з цих проектів коник покрівлі буде мати меншу довжину. Відповідь: довжина коника покрівлі за двома проектами однакова,тобто 30 м.

6. Згідно проектному завданню, елементи кліток сходів повинна задовольняти наступним вимогам: а) сходи повинні бути двомаршові, ширина маршу 1,2 м, б)кут нахилу східного маршу 30⁰, в) ширина кожної східної площадки 1,3 м. Які повинні бути розміри клітки сходу при висоті 3,2 м? Ширина клітки сходів повинна бути 1,2*2 = 2,4 м, довжина – 5,37 м.

При вивченні теми про об’єми многогранників доцільно угледіти розв’язок задач на підрахунок об’ємів земляних робіт при розробці котлованів, виїмок та насипів, тощо, а також задач на витрати будівельних матеріалів при укладки фундаменту будівель, при укладці стін, розробці перекриттів, тощо.Задачі із будівельною тематикою можуть вирішуватися при вивченні питання про нерівності.

7. Для нормального освітлення класної кімнати необхідно, щоб відношення площ вікон та підлоги були не менш 1:5. Яка допустима ширина кімнати, якщо ширина пролому кожного вікна у два рази більше ширини простінка, а висота вікна 2 м?

Відповідь: ширина кімнати не повинна перевищувати 6,7 м.

8. З двох однакових кранів коштовність використання протягом зміни для першого крана дорівнює а₁ гривень, для другого а₂ гривень. Коштовність монтажу та демонтажу для першого крана дорівнює в₁ гривень, для другого в₂ гривень (а₁<а₂ , в₁>в₂). За якою довжиною праці будівельного об’єкта доцільніше застосовувати перший кран? Відповідь:кран доцільніше застосовувати при довгій праці більш ніж (а₁-а₂) /(в₁-в₂).

При вивченні матеріалу про тіла обертання доцільно розглянути розв’язання задач на обчислення об’єму піску, яке сипали до купи; задач на обчислення діаметрів водопровідних труб, які постачають визначену кількість води; задач на обчислення об’ємів та ваги панелі, які полегшили за рахунок порожнечі, тощо.

9.Маємо водогінної труби діаметром 25; 32; 50 і 70 мм. Для будівельної площадки треба постачання 10 куб.м води на годину. Якщо прийняти швидкість води в трубах 1,5 м/хв., треба визначити, який діаметр повинна мати труба водогінна.

10.Для полегшення ваги в панелях міжповерхневих перекриттів роблять порожнечі. Рахуючи,що панель зроблена з однорідного матеріалу, визначити, на скільки відсотків можна знизити вагу панелі, яка має розміри 586*119*22 см, зробивши порожнечі циліндричної форми так, щоб товщина слою бетону ніде не була менше 3,5см, а вісі циліндрів були паралельні ребру, рівному 586 см.Відповідь: 40,5%.

Похідна та її застосування при розв’язанні прикладних задач

За допомогою диференціального числення було розв’язано цілу низку задач теоретичної механіки, фізики та астрономії. Зокрема, використовуючи методи диференціального числення, вчені передбачили повернення комети Галлея, що стало тріумфом науки XVIII ст.За допомогою саме цих методів математики у XVIII та XIX ст. вивчали різні криві: знайшли криву, якою найшвидше падає матеріальна точка; навчились знаходити кривизну ліній.І сьогодні поняття похідної знаходить широке застосування в різних сферах науки та техніки. Постановка проблеми допомагає з’ясувати:

яким повинен бути кут прилягання під’їзного шляху до магістралі, щоб сумарний річний пробіг автомобілів з одного пункту до двох інших був найменшим.
при якому куті нахилу бічних сторін переріз зрошувального каналу буде мати максимальну площу.
знайти найбільш економну швидкість океанського танкера.

Задачі:

З’ясуйте, який повинен бутикут прилягання під’їзного шляху СЕ до магістралі АВ, щоб сумарний річний пробіг автомобілів з С до А та В був якомога меншим. Відомо,що рух між С і А буде вдвічі інтенсивнішим, ніж С і В; АВ=100 км; АС=30 км.

Нехай n – кількість рейсів, що планується в середньому протягом року з С до В. тоді сумарний річний пробіг автотранспорту з С у А та В можна підрахувати так: S(x) = 2nAC+nCE+nBE = 2n(AE+EC)+n(EC+BE) = 2nAE+2nEC+nEC+nBE =

= 2nAE+3nEC+nBE = nAE+nAE+nBE+3nEC = 3nEC+nAB+nAE = nAE+nAE+

+nBE+3nEC = 3nEC+nAB+nAE = n(3EC+AB+AE). S(x) = n(3EC+AB+AE).

З формули бачимо, що точку прилягання немає сенсу вибирати праворуч від D, оскільки у цьому випадку СЕ>CD, AE>AD, і тому значення S буде більшим, ніж при E=D. Тому х=[α;π/2]. Виразивши з прямокутного трикутника CDE довжини сторін СЕ і DE через CD та х, дістанемо:

S(x) = m (90/sinx – 30ctgx+140), х є [α;π/2].

Знайдемо найменше значення функції на заданому відрізку.

Sˈ(x) = (90m(1/3 – cosx) / sin²x, Sˈ(x) = 0, 90m(1/3 – cosx) = 0,

cosx = 1/3, x = arccos1/3 = 70⁰

x – єдина критична точка функції Sˈ(x), так як Sˈ(x)<0 при хє [α;х), Sˈ(x)>0 при хє [х;π/2]. При х = 70⁰ функція набуває найменшого значення. Кут прилягання під’їзного шляху до магістралі повинен наближено дорівнювати 70⁰.

Зрошувальний канал має форму рівнобічної трапеції, бічні сторони якої дорівнюють меншій основі. При якому куту нахилу бічних сторін переріз каналу буду мати максимальну площу?

Розглянемо прямокутний трикутник АВМ АМ=asinφ, BM = acosφ.

BM = CK = acosφ, BC = a+ 2acosφ.

S(ABCD)=(AD+BC)/2*AM;S(ABCD)= =(a+a+2acosφ)_*asinφ=(2a+2acosφ)_*asinφ= =(a(1+cosφ))asinφ=a²sinφ(1+cosφ).

Ми дістали F(φ) = a²sinφ(1+cosφ). Знайдемо найбільше значення функції

Fˈ(φ) = a²(cosφ (1+cosφ)) + sinφ(-sinφ) = a²(cosφ+cos²φ- sin²φ) = a²(cosφ+cos²φ+ +cos²φ-1) =a²(cosφ+2cos²φ -1).

Fˈ(φ) = a²(2cos²φ+cosφ -1), Fˈ(φ) = 0,a²(2cos²φ+cosφ -1) = 0,

cosφ = (-1+3)/4 = 1/2, φ = 60⁰.

Переріз зрошувального каналу буде мати максимальну площу при куту нахилу бічних сторін 60⁰.

Витрати на паливо, що необхідне для руху океанського танкера, пропорціональні кубу його швидкості та складають 20 у.о. За годину за швидкість 16 вузлів (вузол дорівнює морській милі за годину), а всі інші витрати складають 100 у.о. за годину. Знайти найбільш економну швидкість руху за тихої погоди. Обчисліть додатковий прибуток, якщо відстань до порту призначення 100 морських миль(морська миля – 1852 м).

Нехай х вузлів – найбільш економічна швидкість океанського лайнера 20/10³_*х³=0,02х³(у.о.) – витрати палива за швидкості х вузлів; 100/х (год) – час руху, за який танкер пройде 1000 морських миль. Складемо функцію витрат коштів за один рейс: Р= 1000*0,02*х³/х (у.о.)

Враховуючи 1 інші види витрат, що складають 100 у.о. за годину, дістанемо:

Р= 1000*(0,02 х³+100) /х (у.о.)

Знайдемо найменше значення функції

Рˈ= (1000(0,02х²+100/х))ˈ=1000(0,04х – 100/х²)

Рˈ(х) = 0 1000(0,04х – 100/х²)=0 0,04х³=100 х ≈ 13,6.

Рˈ(10) = 1000(0,04*10 – 100/10³) < 0; Рˈ(15) = 1000(0,04*15 – 100/15³) > 0.

Таким чином, 13,6 вузлів є найбільш економною швидкістю. Слід врахувати, що за малої швидкості на одну милю шляху витрачається багато часу і, отже підвищується вартість утримання команди, за дуже великої швидкості витрачається багато палива. Тому, 13,6 вузлів є найраціональнішою швидкістю.Обчислимо витрати коштів на 1000 морських миль за швидкості 10 та 13,6 вузлів. Рˈ= (1000(0,02*10³+100))/10 = 12000 (у.о.);

Рˈ= (1000(0,02*13,6³+100))/13,6 = 11030 (у.о.).

Додатковий прибуток становить 12000 – 11030 = 970 у.о.

Креслення, як графічна підготовка учнів до життя

Необхідність підвищення рівня графічної підготовки учнів та розвитку їх уявлень про простір потребувала сучасна програма геометрії і креслення в школі. Таким чином маємо чотири показника: 1. вміння читати креслення, 2. вміння їх виконувати, 3. знання умовностей технічного креслення, 4. розвиток уявлень про простір.

З цією метою в кінці кожної учбової чверті учні виконують контрольні роботи, зміст яких показан на кресленнях. Ці контрольні роботи були складені з урахуванням вивченої графічної підготовки учнів. При цьому керівна роль придавалася вивченню умов розвитку розуміння учнів, а не техніці побудови зображень за допомогою інструментів для креслень.

Кожна з контрольних робіт виконується протягом одного уроку (45 хвилин). Цього часу достатньо, так як кожен учень получає бланк із завданям, на якому є місце для виконання цього завдання.

Одна із особливостей контрольних робіт складалася у тому, що вони були складені в двох варіантах: більш простому і підвищеної складності. Так, наприклад, у завданні для I семестру при аналізі зображень групи геометрічних тіл у варіанті I проекції кожного тіла відокремлені один від іншого і чітко проглядуються, а у варіанті II ці проекції взаємно перекривають одна одну та виявлення кожної з них потребує ретельного аналізу зображень.

$C:\Users\ARIS 057 761 50 28\Desktop\2014-12-25\002.jpg$

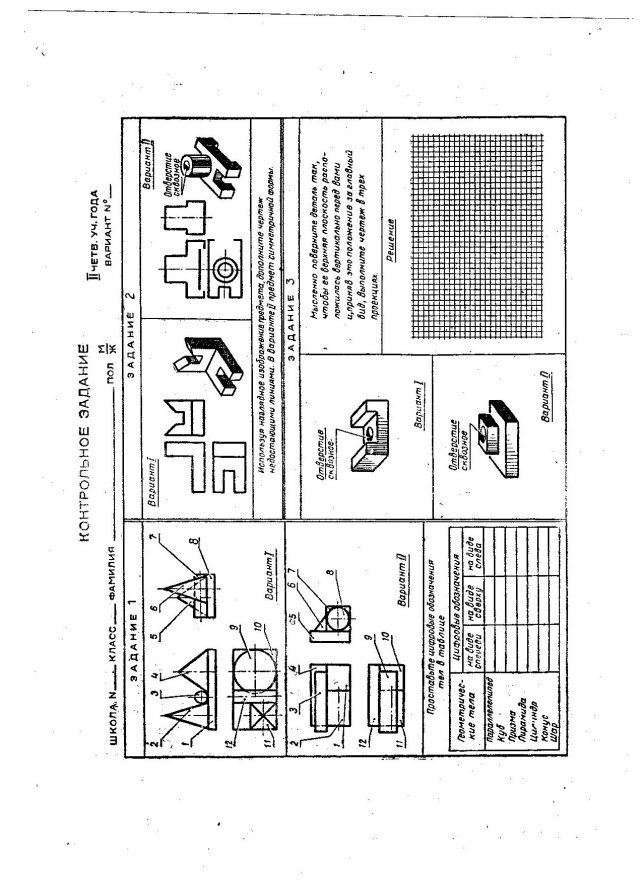
$C:\Users\ARIS 057 761 50 28\Desktop\2014-12-25\003.jpg$

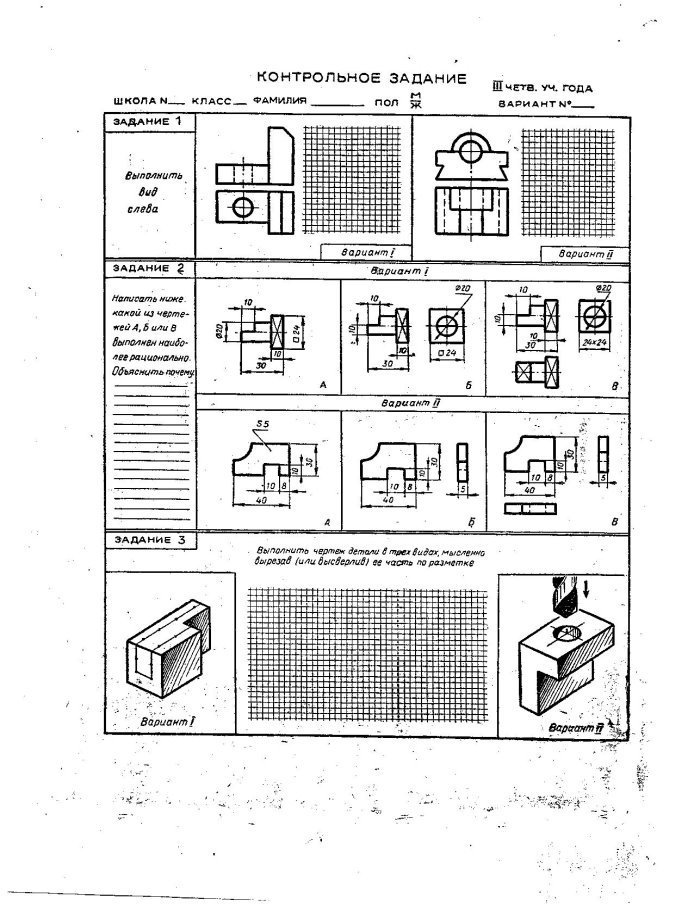
$C:\Users\ARIS 057 761 50 28\Desktop\2014-12-25\001.jpg$

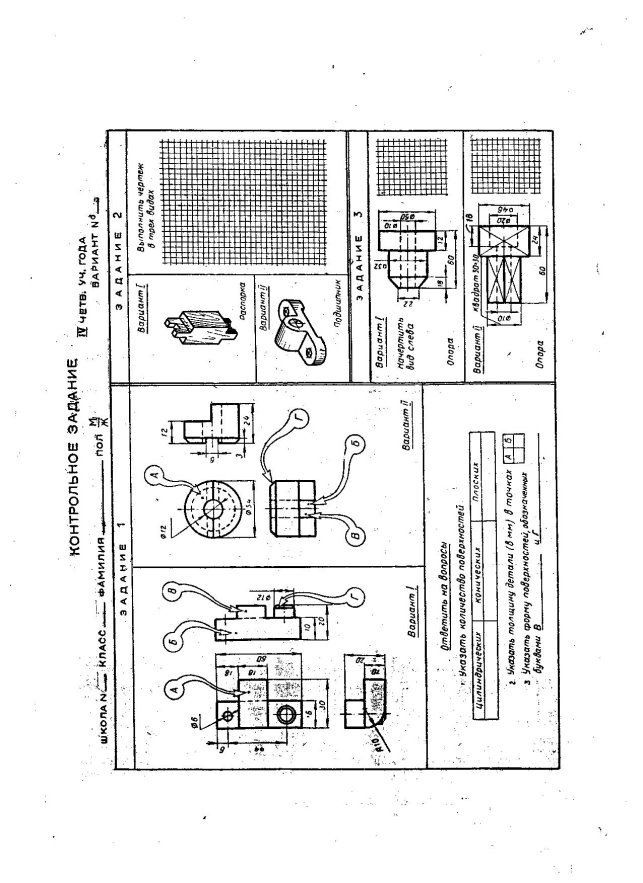
$C:\Users\ARIS 057 761 50 28\Desktop\2014-12-25\004.jpg$

Лабораторно - графічні роботи та їх призначення

Характерними особливостями лабораторно-графічних робіт є: а) побудова графіків і їх застосування; б) використання креслень, вимірювальних інструментів та інструментів для підрахунків, приборів, спеціальних лекал; в) обробка результатів вимірювань за допомогою необхідних формул і порівняння результатів вимірювань; г) використання таблиць, довідкової літератури, підручників або інструкцій. Лабораторно-графічні роботи мають велике виховне та освітнє значення. Вони дозволяють повніше з’ясувати математичні залежності між величинами, ознайомитися з вимірювальними інструментами та їх застосуванням на практиці, навчитися вимірювати та обчислювати із визначеною точністю. Індивідуальна робота учнів виробляє вміння вірно, охайно та чітко виконувати креслення, проводити підрахунки. Лабораторно-графічні роботи дають можливість удосконалювати навички наближених обчислень, практику роботи з математичними таблицями, а також утворюють тісні зв’язки між різними розділами курсу математики и між різними розділами шкільних курсів. При проведенні лабораторно-графічних робіт графічний метод застосовуємо також при дослідженні функцій, розв’язку рівнянь, нерівностей, систем рівнянь та нерівностей, тощо. Він не викликає такого розумового стомлення, як це відбувається при аналітичному способі. Велике значення графічного метода и для політехнічного навчання, так як він широко застосовується в техниці для розв’язку цілого ряду виробничих задач.

При виконанні лабораторно-графічних робіт необхідно мати у кабінеті такий комплект учбового обладнання: інструменти для креслення, вимірювання та обчислення, комплекти для самостійних та лабораторних робіт, картки-завдання за темами, таблиці, тощо. З інструментів для креслення та вимірювання в кабінеті має бути в достатній кількості масштабні лінійки, трикутники двох видів (один з кутами 90, 45 до 45°, а другий із кутами 90, 60 і 30 °), циркулі, транспортири, готовальні, координатна дошка, штемпелі, лекала. Деякі з лекал можна виготовити учнями як домашнє завдання.

Кожна лабораторно - графічна робота складається з восьми варіантів та містить матеріал, який охоплює всю тему і пропонується після огляду теоретичного мaтeріалу, прикладів та моделей. Для кожного варіанту готують картки. Лабораторно–графічні роботи включають у собі завдання різного ступеню складності. Це дозволяє вчителю індивідуалізувати роботу учнів. Іноді лабораторно–графічні роботи виконуються частково і пропонуються учням до виконання при повторенні матеріалу в кінці чверті, семестру або навчального року. Правильна організація лабораторно-графічних робіт виховує культуру праці (вміння організувати робоче місце, тримати його та обладнання в порядку), звичку до систематичної роботи, повагу до праці, прихильність до навчання і постійного вдосконалення знань і навичок, зберігати власність, свідомо дотриматися дисципліни; розвиток допитливості, дотепності, почуття відповідальності і естетичного смаку учнів. Витончено виконана робота є внеском у розвиток почуття краси.

Лабораторно-графічна робота за темою:

«Координатна площина. Послідовності та їх границі»

(1 год.)

Мета роботи – закріпити поняття послідовності та навичок зображення множин заданих точок і послідовностей на координатній площині.

Обладнання - карточки із завданням, олівець, міліметровий папір.

Завдання|

I.Зобразити в координатній площині множину точок {(х;у)| а |х| +b|y|=cx +dy}. Чи належить даній множині точки А(a;b), B(c;d)?

II. 1. Виписати послідовність (u_n), якщо u_n = (pn+q) /n.

2. Зобразити члени послідовності(u_n):

а) точками координатної прямої,

б) точками координатної площини.

3. Чи є послідовності(u_n) монотонною?

4. Чи існує таке число, до якого наближається послідовність(u_n)?

III. Побудуйте геометричну фігуру, обмежену графіком функції y=kx, відрізком [0;х₁] вісі абсцис та прямої х=х₁. Поділити відрізок [0;х₁] вісі абсцис на n рівних частин і на побудованих відрізках побудувати вписані прямокутники. Знайти площу геометричної фігури як границю послідовності (S_n)площин утворених ступінчатих фігур.

З р а з о к в и к о н а н н я р о б о т и

Картка №1

a=2, b=-1, c=-2, d=1 II . p=2, q=4III.k=1/2 x₁=8

О ф о р м л е н н я р о б о т и у ч н е м

{(х;у) |2|х| + |y| = -2x + y}.

Розглянемо по черзі всі чверті:

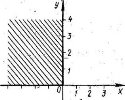У першій чверті |x|=x, |y|=y, 2x+y=-2x+y<=>x=0

У другій чверті|x|=-x, |y|=y, -2x+y=-2x+y<=> 0=0

У третій чверті|x|=-x, |y|=-y, 2x-y=-2x+y<=>y=0

У четвертій чверті|x|=x, |y|=-y, 2x-y=-2x+y<=>2 x=y.

Точка А(2;1) даній множині не належить, а точка В(-2;1) належить.

u_n = (pn+q) /n

1.u₁=6; u₂=4; u₃=3⅓; u₄=3;u₅=2,8; u₆=2⅔; u₇=2⅞; u₈=2,5;…;u_n = (pn+q) /n.

2. послідовність є монотонною та граничною.

3. границя послідовності існує та дорівнює 2.

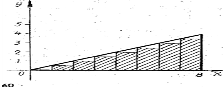
Сторони кожного з (n - 1) прямокутників (вони складають ступінчату фігуру) дорівнюють 8/n, а інші сторони утворюють арифметичну прогресію: 4/n; 4/n*2; 4 /n*3; …; 4/n*(n-1).

$C:\Users\ARIS 057 761 50 28\Desktop\работа\печатки\media\image25.jpeg$ Тому

S_n= =8/n*4/n+8/n*4/n*2+8/n*4/n*3+…+8/n*4/n*(n-1)= =8/n*4/n*(1+2+3+…+(n-1)) =

=32/n²_*n(n-1)/2 = 16(n-1)/n.

S = limS_n = lim 16(n-1)/n = 16

Зауваження.

При виконанні роботи учням пропонуються вісім різних варіантів.

_дані^{варіант}	I	II	III	IV	V	VI	VII	VIII
a	2	-2	2	-2	1	-1	2	-3
b	1	1	3	-3	-1	1	-1	2
c	-2	2	3	2	1	1	1	-3
d	1	1	2	-3	1	-1	2	2
p	2	2	4	4	-2	-4	3	-3
q	4	-4	1	-1	6	-6	2	2
k	0,5	1/3	0,25	1	-0,5	-1/3	-0,25	-1
x₁	8	9	16	4	8	9	16	4

Лабораторно-графічна робота за темою:

«Функції. Неперервні та перевні функції. Границя функції»

(1год.)

Мета роботи—закріпитизагальні поняття, засоби завдання і геометричнізображенняфункцій, уявленняпро неперервніи перервніфункції.

Обладнання:карткиіз завданням, міліметровийпапір,олівці, лінійки, циркулі.

Завдання

I. 1. Побудувати графік функції

0 при х< — а,

у = b при х= -а,

а² — х²при |х|<а,

х—а + 1 при х > а(а> 0),

2. Вказати, в яких точках дана функція неперервна, а в яких перервна. Визначити значення функції в точках разриву.

3.Чомудорівнює границя функції при х—а?

II. По даному графіку знайти аналітично задані функції (функцію задану формулою) і визначте: а) область визначення; б) область значення; в) проміжки зростання и спадання; г) точки максимуму і мінімуму.

З р а з о к в и к о н а н н я р о б о т и

Картка №1

0 при х< -1

у = 2 при х=- 1

V 1-x²при |x|<1

х при х ≥ 1

О ф о р м л е н н я р о б о т и у ч н е м

I.1.

2. Функція має розрив при будь-якому х - 1 та х 1;

у(-1)=2 та у(1)=1.

3. limу = 0

ⁿ^¬œ

II. 3 при х< — 2,

у= x² при -21

-х+1 прих >1

а) ]-[ ; б) ]-] ; в) зростає на проміжку ][, спадає на проміжку ][ і ][, постійна на проміжку ]-]; х=0 є точкою мінімуму, у_min=-1, а х=1 – точка максимуму, у_max=0.

Зауваження.

При виконанні роботи учням пропонується вісім різних варіантів.

	I	II	III	IV	V	VI	VII	VIII
а	1	1,5	2	2,5	3	3,5	4	0,5
b	2	-2	1	-1	4	-4	3	-3

Лабораторно-графічна робота за темою

«Похідна та її застосування до дослідження функції»

(1год.)

Мета роботи — закріпити навички побудови та читання графіків, вміння застосовувати похідну до дослідження функції.

Обладнання: картки із завданням, міліметровий папір,олівці, лінійки, математичні таблиці.

Завдання

I. Для функції у=1/5 (х³ +mx² +nx +p) знайти: а) область визначення;

б) похідну; в) критичні точки; г) проміжки монотонності та екстремуми. Побудуйте графік.

II. Написати рівняння дотичної до графіка даної функції до осі абсцис під кутом 45⁰.

З р а з о к в и к о н а н н я р о б о т и

Картка №1

у=1/5 (х³ +8x²- 11x- 30)

О ф о р м л е н н я р о б о т и у ч н е м

1.а) ]-[; б) уˈ(х) =1/5_* (3х² +8x- 11)= 3/5 (х+11/3)_*(х-1); в) критичні точки:

-11/3, 1; г) за результатами досліджень складаємо таблицю

х	-	x=-3	-	x=1
уˈ(х)	+	0	-	0	+
у(х)	зростає	2+ 26/27	спадає	-7- 1/5	зростає
max,min		max		min

та будуємо графік функції

2.Похідна фінкції у=у(х) при х=х₀ дорівнює тангенсу кутів нахилу дотичної до графіку цієї функції у точці з абсцисою х_0.Так як tg45⁰ =1, то розв’язок рівняння1/5 (3х₀² +8x₀- 11) =1 х₀₁ =-4, х₀₂ =4/3. Підрахуємо значення функції в цих точках: f(-4) = 2,8, f(4/3) =-7 1/27.

Запишемо рівняння дотичної в цих точках: 5х-5у+34=0; 27х-27у-226=0.

Зауваження.

При виконанні роботи учням пропонуються вісім різних варіантів.

_дані^{варіант}	I	II	III	IV	V	VI	VII	VIII
a	1	-1	-2	2	4	-4	6	-6
m	4	1	-2	-5	-8	-11	7	10
n	-11	-16	-15	-8	-5	24	0	17
p	-30	-16	0	12	14	0	-36	-28

Лабораторно-графічна робота за темою:

«Обчислення площі фігур, обмежених криволінійним контуром»

(1год.)

Мета роботи — закріпитинавички застосування визначеного інтегралу, до обчислення площ криволінійних трапецій.

Обладнання: картки із завданням, міліметровийпапір,олівці, масштабні лінійки, циркулі-вимірювачі, лекала.

Завдання

I. Побудувати геометричну фігуру, обмежену графіком функції:

0,5х² +bx +c, якщо х₁х₂,

у= - х + р, якщо х₂х₃ ,

та прямими х = х₁, х = х₃ , у = 0.

II. Знайти площу фігури двома засобами:

1. За формулою S = ʃ_a^bf(x)dx

2.Наближено, розбиваючи відповідно фігуру на n криволінійних трапецій і замінюючи кожну з них відповідною прямокутною трапецією, тобто за формулою S₁= (b –a)/n*[1/2 y₀+y₁+y₂+…+y_n_-1+1/2 y_n], де n=10.

Порівняти здобуті результати. Знайти абсолютну та відносну похибку:

ΔS = S – S₁, P = ΔS/S.

Результати обчислень та вимірювань вносити до таблиці:

Х₁

ΔS

У₁

S₁=

З р а з о к в и к о н а н н я р о б о т и

Картка №1

0,5х² +2x +3, якщо -3,

у= - х + р, якщо 0.

О ф о р м л е н н я р о б о т и у ч н е м

I. Будуємо параболу у=0,5х² +2x +3 для [ -3; 0]. Парабола перетинає вісь ординат у точці з координатами (0;3). Знайдемо точки перетину параболи у=0,5х² +2x +3 з прямою у =3. Для цього підставимо до рівняння

х	-3,0	-2,0	-1,0	0,0
у	1,5	1,0	1,5	3,0

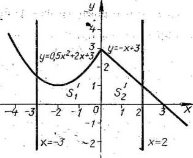у=0,5х² +2x +3 значення у=3: 3=0,5х² +2x +3. Корені рівняння -4 та 0, тобто пряма та парабола перетинаються у точках з координатами (-4;3) і (0;3), які симетричні відносно вісі симетрії параболи. Абсциса вершини параболи дорівнює (-4+0)/2= - 2, а ордината у=0,5*(-2)²+2*(-2)+3=1. Таким чином, вершина параболи має координати (-2;1). Вибираємо декілька контрольних точок:

Будуємо параболу із за допомогою лекала параболи у=0,5х² так, щобгострі олівці пройшли через контрольні точки. Пряму у = -х+3 для ] 0; 2] побудуємо за двома точками (0;3); (2;1).

II.1) S=S^ˈ₁ +Sˈ₂ = ʃ_-3⁰(0,5х² +2x +3)dx + ʃ₀²(-x+3)dx =

=[ 0,5* х³/3 +2*х²/2 +3х]_-3⁰ + [ -х²/2 +3х]²₀ = 8,5.

x_i	-3,0	-2,5	-2,0	-1,5	-1,0	-0,5	0,0	0,5	1,0	1,5	2,0	S=8,5	ΔS	P
y_i	1,5	1,1	1,0	1,13	1,5	2,13	3,0	2,5	2,0	1,5	1,0	S=8,57	0,07	1%

Зауваження .

При виконанні роботи учням пропонуються вісім різних варіантів.

_дані^{варіант}	I	II	III	IV	V	VI	VII	VIII
b	2	1	0	-1	-2	3	4	5
c	3	1,5	1	1,5	3,0	5,5	9	13,5
p	3	4	5	6	7	2	1	0
x₁	-3	-2	-1	0	1	-4	-5	-6
x₂	0	1	2	3	4	-1	-2	-3
x₃	2	3	4	5	6	1	0	-1

Висновок

Задачи прикладного змісту мають велике виховне та освітнє значення, так як відповідають на питання: «Навіщо вивчати математику?». Вони дозволяють повніше усвідомити математичний зв'язок між величинами, між різними розділами курсу математики, зв'язок з іншими предметами шкільного курсу та життя, як то: економіка виробництва; фінансова справа; електроніка; програмування; фізика; хімія; радіофізика, тощо.

Роботи з наведеними особливостями викладання математики дозволяють розвивати пізнавальний інтерес, навички колективної праці, вміння використовувати сформовані знання, навички й уміння в нових ситуаціях; формувати навички взаємоконтролю та самоконтролю. Матеріал прикладної спрямованості дає змогу вчителям розширювати світогляд учнів, полегшувати розуміння суті методу математичного моделювання. З досвіду можу сказати, що такі форми роботи й підбір матеріалу дуже зацікавлюють школярів і спонукають до активної участі на кожному уроці.

Методичні матеріали призначені для вчителів математики загальноосвітніх навчальних закладів.

Список використаних джерел

Саломатнікова О.М. Похідна та її застосування при розв’язанні прикладних задач.-К.: Математика в школах України, 2006. -№30–С.17-19
Найдьонова О.О. Педагогічні функції прикладних задач. -К.: Математика в школах України. 2009. -№30.–С.17-19
Ботвинніков А.Д. Рівень та особливості графічної підготовки учнів. Москва, 1970. – С.46-52
БондаренкоА.С., Щепетев А.Н. Задачі з виробничим змістом. Новокузнецьк, 1977 р. –С. 32-34
ЮртаєваГ.Т. Лабораторно - графічні роботи з алгебри та початкам аналізу. Посібник для вчителів.– М: Просвещение, 1978 р.-80 с., ил.

[Введите текст]

docx

Завантажити

Зберегти на потім

Додав(-ла)

Каліта Емма Євгеніївна

Пов’язані теми

Алгебра, 11 клас, Матеріали для друку

Додано

3 квітня 2020

Переглядів

1573

Оцінка розробки

Відгуки відсутні