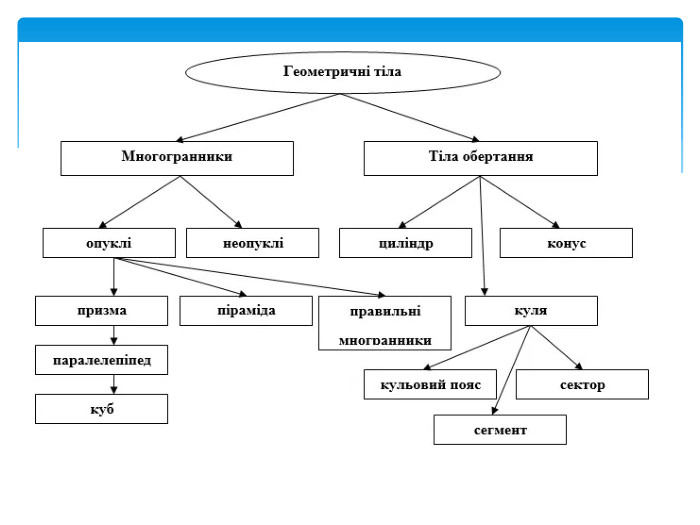
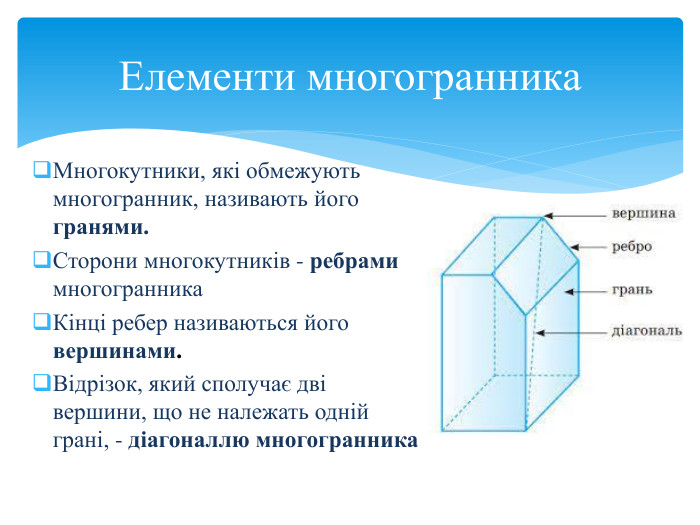
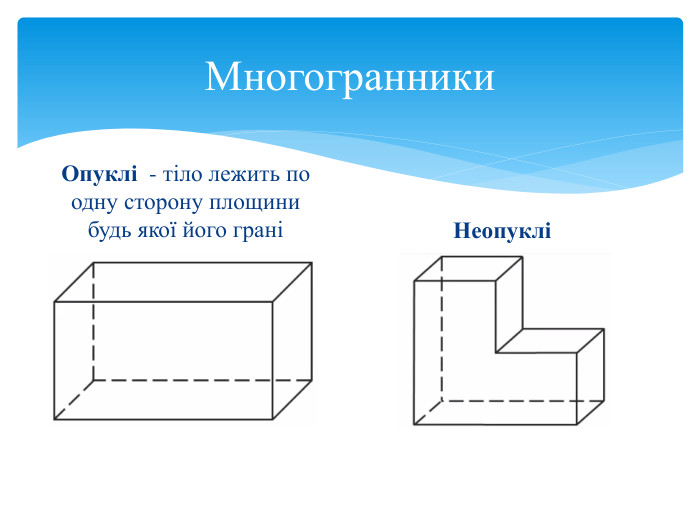
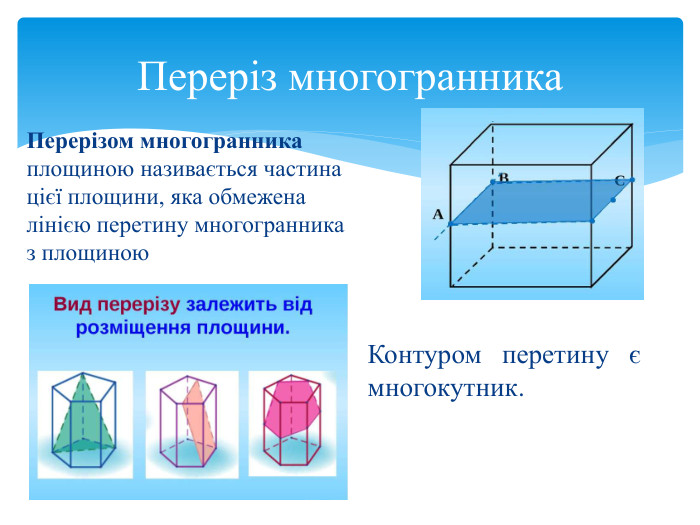
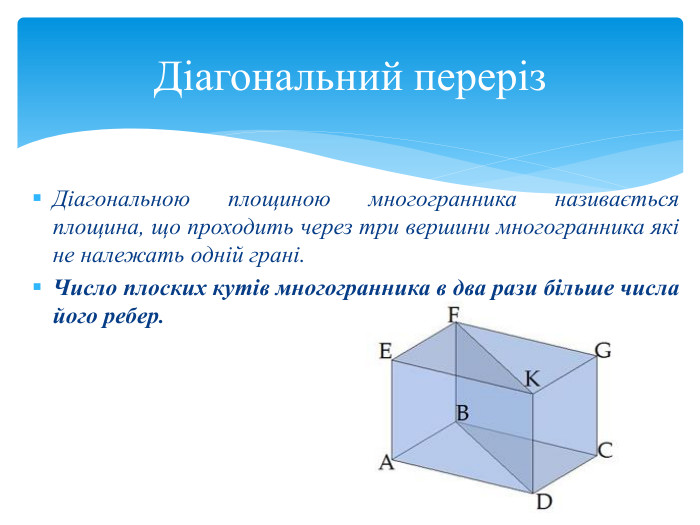
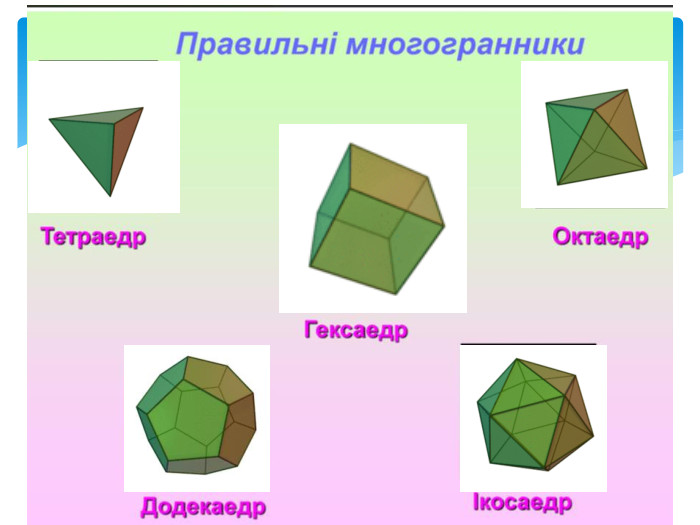
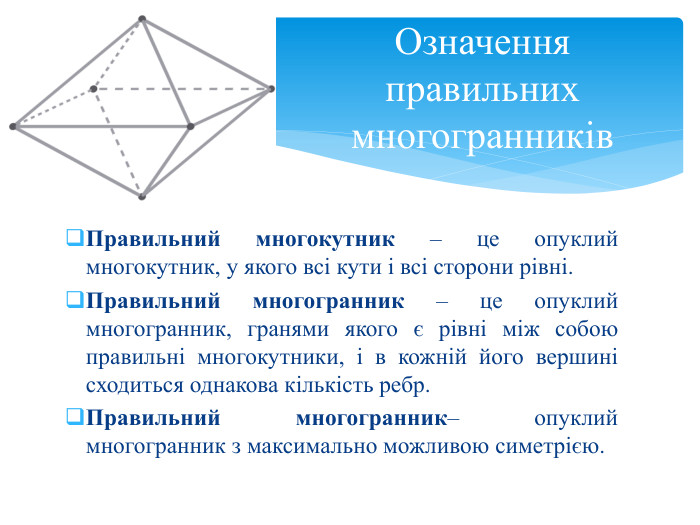
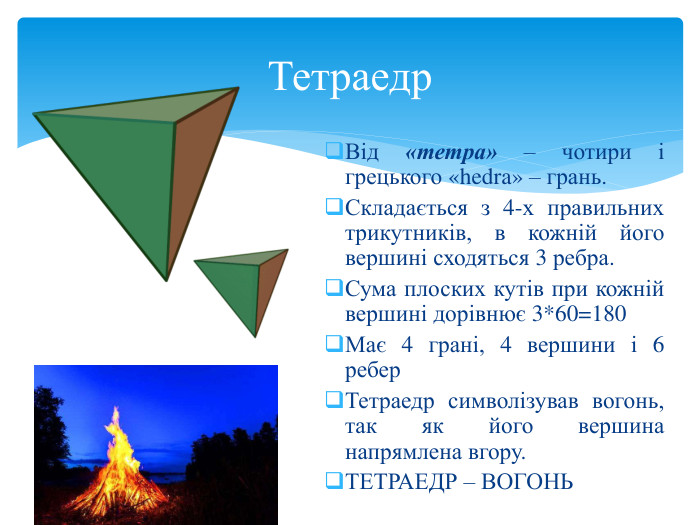
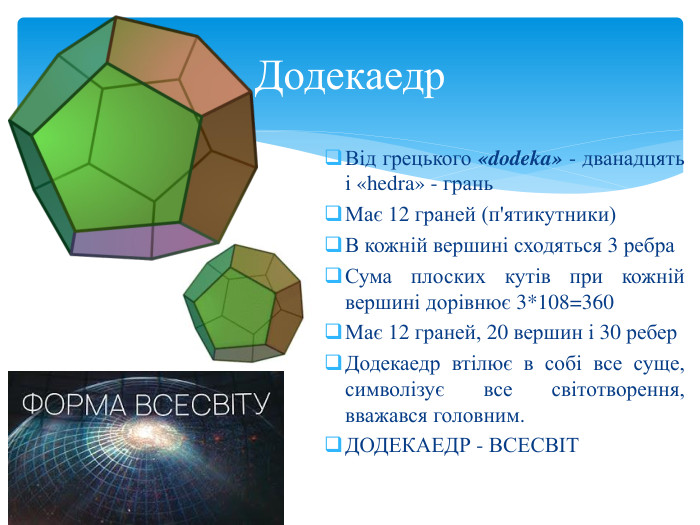
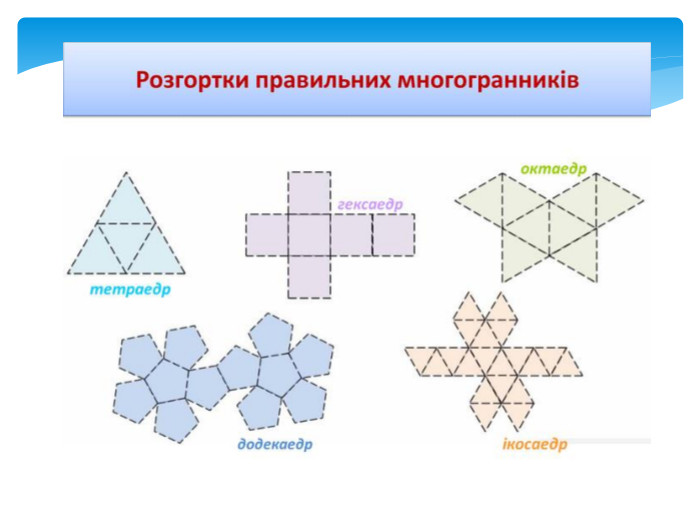
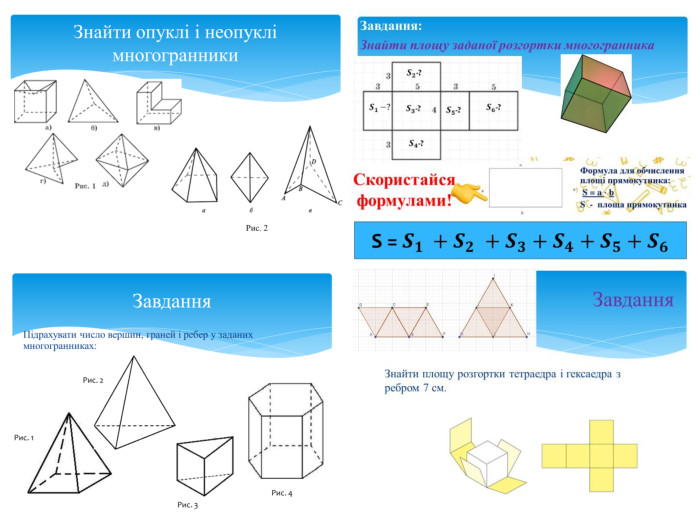
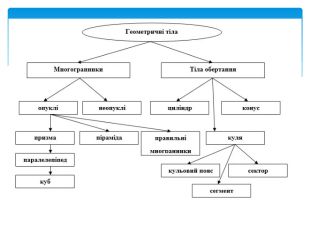
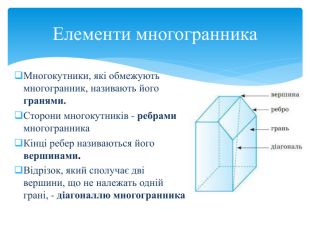
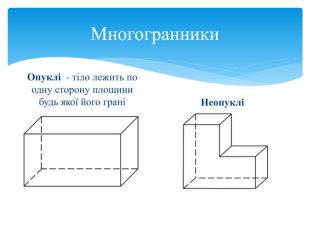
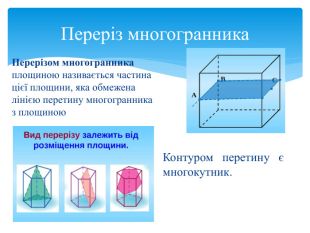
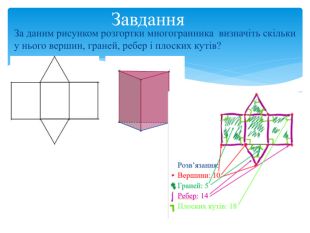
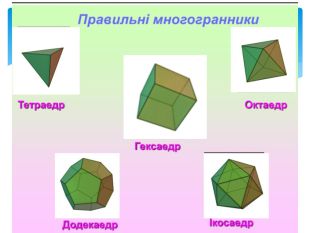
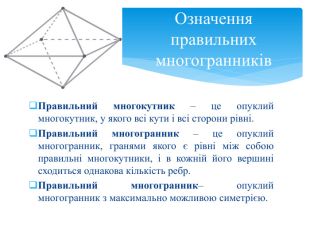
Тема 1. МНОГОГРАННИКИ. Многогранник та його елементи. Опуклі многогранники
Про матеріал
Ознайомити учнів з поняттям про багатогранник та їх
основними елементами, з поняттям про правильні
багатогранник, їх основні властивості;
розвивати спостережливість, логічне мислення, просторову
уяву ;
виховувати математичну культуру мовлення,
інтерес до вивчення математики, естетичні смаки
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Щиро дякую за Вашу роботу!
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку