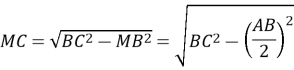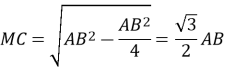Тема 1. МНОГОГРАННИКИ. Многогранник та його елементи. Опуклі многогранники

21 вересня

Тема: Розв’язування типових вправ

1. Розв’язування задач

№1

Призма має 7 граней. Який многокутник лежить у її основі?

 

Відповідь:

 

Основою є п’ятикутниик

 

 

•      Якщо призма має 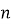-граней

(Основою буде – кутник)

 

 

 

 

№2

У якій призмі бічні ребра паралельні її висоті?

 

Відповідь: у прямій

 

№3

Основою прямої призми є рівнобічна трапеція, один із кутів якої дорівнює . Знайдіть двогранні кути призми при її бічних ребрах

 

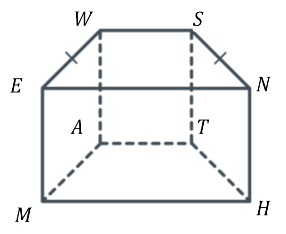
Дано:

– пряма призма

– рівнобічна трапеція

 

Знайти:

Двогранні кути при бічних ребрах

 

 

 

 

Розв’язок:

 

Двогранний кут дорівнює відповідному йому лінійному куту, так за умовою маємо пряму призму, то:

Двогранні кути при ребрах дорівнюють

Двогранні кути при ребрах дорівнють

 

Відповідь:

 

№4

Знайдіть площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює , а висота дорівнює

 

Дано:

Правильна чотирикутна призма

Основа призми – квадрат із стороною

Висота призми –

 

Знайти:

 

Розв’язок:

 

Відповідь:

 

№5

Точки – середини ребер правильної призми . Площина, яка проходить через пряму та утворює з площиною кут , перетинає ребро у точці . Знайдіть площу утвореного перерізу призми, якщо сторона її основи дорівнює 12 см

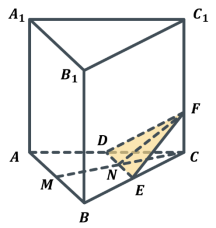
Дано:

– правильна призма

Кут між площинами дорівнює

см

 

Знайти:

Розв’язок:

 

 

Якщо учні не пам’ятають матеріалу з попередніх класів, можна довести, що :   Так як

 

 

Розглянемо

 

 

Відповідь:

№6

Основа прямої призми – ромб зі стороною і гострим кутом . Більша діагональ призми утворює з площиною основи кут . Знайдіть висоту призми.

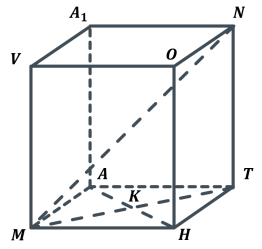
Дано:

 

Знайти:

 

 

 

Розв’язок:

Так як проекцією більшої діагоналі на основу призми буде більша діагональ ромба

В прямокутній призмі бічні ребра дорівнюють висоті.

 

Розглянемо

 

Розглянемо

 

Відповідь:

№7

Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює 12 см і нахилена до площини основи під кутом

Дано:

квадрат

 

Знайти:

 

 

 

Розв’язок:

 

Розглянемо

 

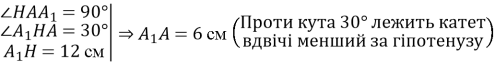
Розглянемо квадрат

 

 

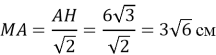
Відповідь:

№8

Кожне ребро правильної призми дорівнює .

Знайдіть:

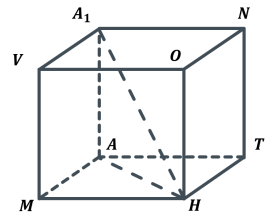
1.     Площу перерізу призми, який проходить через точки
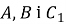
2.     Кут між площиною даного перерізу та площиною основи призми

 

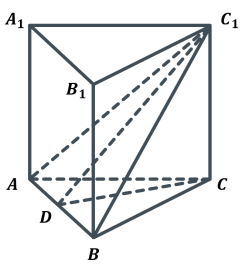
Дано:

– правильна призма

Всі ребра дорівнюють

 

Знайти:

 

 

 

 

Розв’язок:

Розглянемо

 

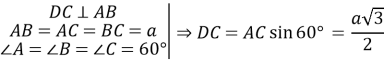
Розглянемо

 

 

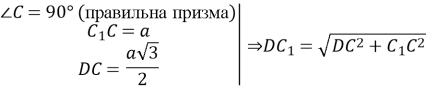
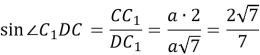
Відповідь: