Тема: Площі плоских фігур

Урок геометрії у 8 класі 

Тема: Площа трапеції

Мета уроку:

•                       Формування вміння оперативно приймати рішення в умовах дефіциту часу, розвивати гнучкість, економічність мислення;
•                       Організувати повторення і поєднати великий об’єм теорії в одну збільшену одиницю;
•                       Показати багатогранність та красу математичних рішень, створити ситуацію успіху, радощів від самостійного долання труднощів.

Форма організації уроку та навчальної діяльності: парна та групова.

Хід уроку

Організаційний момент:

Учням необхідно прослухати наступні вислови та з’ясувати про яку фігуру йтиметься на уроці, свою відповідь треба обґрунтувати:

• фігура є опуклим многокутником;
• сума її внутрішніх кутів дорівнює 360°;
• існує така сторона, що сума внутрішніх кутів, прилеглих до неї, дорівнює 180°;
• дана фігура добре розбивається на паралелограм і трикутник.

Після обміркування я закріплюю на дошці магнітом «королеву уроку» – трапецію.

Робота в парах з повторення теорії

Учні протягом 2 - 3 хвилин відповідають в парах на запитання, котрі з’являються на екрані. Добре, коли пари складаються з учнів різного рівня обізнаності. У цьому разі один з школярів є консультантом і допомагає пригадати потрібний матеріал товаришеві у випадку виникнення труднощів.

Питання:

•                       Дайте визначення трапеції.
•                       Перерахуйте види та властивості трапеції.
•                       Як розбити трапецію на паралелограм і трикутник?
•                       Що потрібно провести у трапеції, щоб отримати подібні трикутники?
•                       Як розбити трапецію на два прямокутних трикутники і прямокутник?
•                       Як знайти площу трапеції?

Підготовка до виконання групового завдання.

Я пропоную учням  записати у зошитах відповіді на завдання усного тесту,

котрий надалі перевіряється самоперевіркою.

 1. Оберіть трапеції:

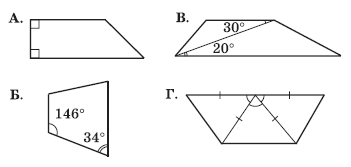
(Відповідь: А, Б, Г.)

2. Оберіть прямокутні трикутники:

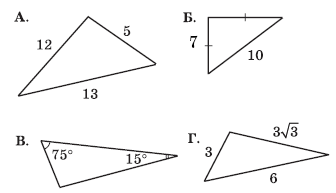
(Відповідь: А, В, Г).

3. Обчисліть площі запропонованих трапецій.

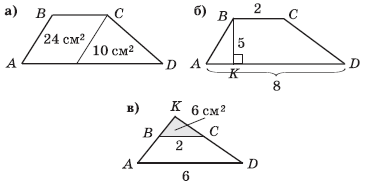
Відповідь: а) 34 см²; б) 25 см²; в) 48 см².

Групова робота

Учням пропонується розв’язати задачу:

Знайти площу трапеції з основами 10 см і 20 см і бічними сторонами 6 см і 8 см.

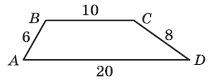
Клас попередньо поділяється на групи однаковими за силою. Кожній групі надається час на пошук та обміркування засобів вирішення задачі. Я виступаю в якості консультанта, якщо потрібно, спрямовую та корегую процес її вирішення. Кожна група обирає одно з рішень і оформлює його у зошиті. На дошці демонструються плани вирішення задачі представниками груп.

Розв’язання. Спосіб І.

1. Проведемо ВН АD и СK АD, тоді чотирикутник HВСK — прямокутник.

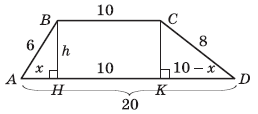
2. Хай АН = x см, тоді KD = (10 – x) см. Використовуючи теорему Піфагора, виразимо висоту h з трикутників АВН и СKD:

h ² = 6² – x², h² = 8² – (10 – x)².

Складаючи та вирішуючи рівняння отримаємо, що h = 4,8 см.

3.Тоді

Спосіб ІІ.

1. Проведемо СН АD и СK АВ, тоді АВСK — паралелограм. Отже,     АK = ВС = 10 см и АВ = KС = 6 см.

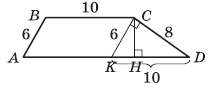
2. Розглянемо трикутник KСD, в якому

KС = 6 см, СD = 8 см, KD = 10 см.

Оскільки KD² = KС² + СD², то згідно теореми, оберненій теоремі Піфагора, трикутник KСD — прямокутний.

3. Можна знайти висоту за формулою:   

4. Площу трапеції знаходимо так же, як і в першому способі розв’язання.

Спосіб ІІІ.

1. Проведемо СK АВ и з’єднаємо точки K і B відрізком.

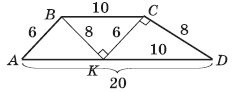
2. Неважко довести, що трикутники АВK, ВKС, KСD рівні та прямокутні.

3.  

Після аналізу всіх рішень, приходимо до висновку, що найбільш раціональним і оригінальним є третій спосіб, а більш природним і звичним – перший.

Дослідження задачі при зміні розмірів фігури.

Після обговорення способів вирішення я пропоную школярам завдання на зміну розмірів фігури. Можна запропонувати відповісти на питання дослідницького характеру:

1. Чи завжди є можливість розбити трапецію на три рівних трикутники?

(З’ясовується, що це можна зробити, тільки якщо одна основа у два рази більша другої).

2. Чи може трапеція бути складена з трьох рівних трикутників іншого виду?

(Трапецію можна скласти з трьох правильних трикутників, рівнобедрених і довільних трикутників).

3. Чи зберігаються способи розв’язання у цих випадках? Які способи будуть більш раціональними?

Перед учнями постає нова проблема: потрібно проаналізувати способи рішення по зміненому кресленню, а також згадати формули для обчислення площі правильного та довільного трикутників. Отже, для правильного трикутника використовується формула: ; для довільного трикутника формула Герона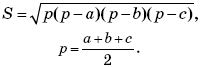

Мається сенс запропонувати школярам, для спрощення обчислювання, довжини сторін прийняти рівними 13, 14 і 15 см, щоб за технічною стороною не загубилася ідея рішення.

Після дослідження задачі на зміну розмірів фігури, я пропоную змінити довжину основ трапеції таким чином, щоб вони відрізнялись одна від одної в два рази. Тоді стає зрозумілим, що трапецію неможливо розбити на три рівних трикутники. Отже наш «гарний» спосіб розв’язання використати неможливо.

У якості домашнього завдання можна запропонувати наступні задачі.

1. Знайдіть площу трапеції, у якої паралельні сторони мають довжину 25 см і 11 см, а непаралельні – 13 см і 15 см.

2. Складіть трапецію з трьох рівнобедрених трикутників, оберіть самостійно довжину сторін і обчисліть площу трапеції.