Урок № 39 з геометрії у 8 класі із розділу « Розвязування прямокутних трикутників» на тему « Співвідношення між сторонами і кутами прямокутного трикутника»
Урок № 39 з геометрії у 8 класі із розділу
« Розвязування прямокутних трикутників»
на тему « Співвідношення між сторонами і кутами прямокутного трикутника»
І. Актуалізація опорних знань учнів.
а) У 8 класі центральна фігура прямокутний трикутник, то повторимо все, що знаємо про прямокутний трикутник.
- Який трикутник називається прямокутним?
- Як називаються сторони прямокутного трикутника?
- Де лежить гіпотенуза?
- Яка основна теорема для прямокутного трикутника?
(Всі до дошки): дано катети 7 см і 24см.
- Що називають синусом гострого кута прямокутного трикутника?
- Що називають косинусом гострого кута прямокутного трикутника?
- Що називають тангенсом гострого кута прямокутного трикутника?
- Що називають котангенсом гострого кута прямокутного трикутника?
б)Перевірка домашнього завдання: Вдома ви повинні були скласти задачу, в якій було відомо дві сторони прямокутного трикутника . Треба було знайти для вашого трикутника синус, косинус, тангенс та котангенс даного гострого кута.
Всі йдуть до дошки, креслять трикутник і розв'язують свою складену вдома задачу.
ІІ. Засвоєння нових знань.
Ми почали розділ « Розв'язування прямокутних трикутників»
Це центральна тема геометрії 8 класу. Ця тема потрібна буде не тільки в подальшому вашому навчанні, але й в майбутньому житті.
2. Проблемна ситуація: Наведу приклад із свого особистого життя. Коли мої діти надумали будувати будинок , стало питання, який буде дах та якою довжиною закупити крокви, щоб дах був красивим. Для цього, потрібно було обчислити сторони прямокутного трикутника за стороною (половиною ширини хати )та відомим гострим кутом , під яким хотілось поставити дах. ( малюнок на дошці). Ширина будинку 8 м, кут 40°. Знайти висоту даху й довжину крокви.
Довелось дати їм урок, який сьогодні у нас з вами за програмою.
Записуємо тему уроку : Співвідношення між сторонами і кутами прямокутного трикутника.
Ми повинні виявити, чи можна знайти сторону прямокутного трикутника через іншу сторону цього трикутника і гострий кут. Якщо можна, то як?
Але головна розвиваюча мета нашого уроку : навчитись спостерігати, порівнювати, запам'ятовувати, застосовувати ці навички при засвоєнні нових знань і розв'язуванні задач.
3. Виводимо формули:( формула,це рівність, яка показує, що знаходимо і як знаходимо) З чого почати? Чи є у нас формули , які пов'язують катет і гіпотенузу, два катети? Так, це синус, косинус, тангенс і котангенс. Отже з них ми можемо утворити нові, потрібні нам формули. Що для цього треба знати? Основні властивості рівностей, які ми вже знаємо. Повторимо їх. Сьогодні нам буде потрібна друга властивість рівностей : обидві частини рівності можна помножати на одне й те саме число, рівність не порушиться.
а)Один учень ( Склярова Леся) виводить першу формулу, тоді другу, тоді записує обидві, видаляє запис на дошці, виводить третю, записує всі три, знову видаляє запис на дошці, виводить четверту, записує всі чотири потім третю, записує всі три, виводить четверту видаляє запис, записує всі чотири і закінчує свою роботу.
б) Мальцев повторює процес, виводить всі формули, і записує всі чотири наприкінці так само як Леся.
в). Павлюк записує формули без виводу
г). Письменський виводить формули для гіпотенузи. Записує всі формули
д). Складаємо опорний конспект:
Дві формули для протилежного катета, дві формули для прилеглого катета і дві для гіпотенузи. Оформлення ОС у кожного своє.
ІІІ. Первинне закріплення знань.
1. Складаємо правила для знаходження невідомих сторін прямокутного трикутника: - як знайти протилежний катет через гіпотенузу; через прилеглий катет і т.д.
2. Розв'язуємо задачі:
1.Дано ; с =10. , α = 40° . Знайти а, в-?
2. Дано : а = 8, β= 70° Знайти: с -? а -?
ІV.Д/з №№ 721. Вивчити формули. Розв'язати №№
Відкритий урок № 39 з геометрії у 8 класі із розділу
« Розвязування прямокутних трикутників»
на тему « Співвідношення між сторонами і кутами прямокутного трикутника»
І. Актуалізація опорних знань учнів.
а) У 8 класі центральна фігура прямокутний трикутник, то повторимо все, що знаємо про прямокутний трикутник.
- Який трикутник називається прямокутним?
- Як називаються сторони прямокутного трикутника?
- Де лежить гіпотенуза?
- Яка основна теорема для прямокутного трикутника?
(Всі до дошки): дано катети 7 см і 24см.
- Що називають синусом гострого кута прямокутного трикутника?
- Що називають косинусом гострого кута прямокутного трикутника?
- Що називають тангенсом гострого кута прямокутного трикутника?
- Що називають котангенсом гострого кута прямокутного трикутника?
б)Перевірка домашнього завдання: Вдома ви повинні були скласти задачу, в якій було відомо дві сторони прямокутного трикутника та один гострий кут. Треба було знайти для вашого трикутника синус, косинус, тангенс та котангенс відомого гострого кута.
Всі йдуть до дошки, креслять тр – к і розв’язують свою задачу.
ІІ. Засвоєння нових знань.
- Ми почали розділ « Розв’язування прямокутних трикутників»
Це центральна тема геометрії 8 класу. Ця тема потрібна буде не тільки в подальшому вашому навчанні, але й в майбутньому житті.
2. Проблемна ситуація: Наведу приклад із свого особистого життя. Коли мої діти надумали будувати будинок , стало питання який буде дах та якою довжиною закупити крокви, щоб дах був красивим. Для цього, потрібно було обчислити сторони прямокутного трикутника за стороною (половиною ширини хати )та відомим гострим кутом , під яким хотілось поставити дах. ( малюнок на дошці). Ширина будинку 8 м, кут 40![]() . Знайти висоту даху й довжину крокви.
. Знайти висоту даху й довжину крокви.
Довелось дати їм урок, який сьогодні у нас з вами за програмою.
Записуємо тему уроку : Співвідношення між сторонами і кутами прямокутного трикутника.
Ми повинні виявити, чи можна знайти сторону прямокутного трикутника через іншу сторону цього трикутника і гострий кут. Якщо можна, то як?
Але головна розвиваюча мета нашого уроку : навчитись спостерігати, порівнювати, запам’ятовувати, застосовувати ці навички при засвоєнні нових знань і розв’язуванні задач.
3. Виводимо формули: З чого почати? Чи є у нас формули , які пов’язують катет і гіпотенузу, два катети? Так, це синус, косинус, тангенс і котангенс. Отже з них ми можемо утворити нові, потрібні нам формули.
а)Один учень ( Склярова Леся) виводить першу формулу, тоді другу, тоді записує обидві , потім третю, записує всі три, виводить четверту, записує всі чотири.
б) Мальцев повторює процес, записує всі формули,
в). Павлюк записує формули без виводу
г). Письменський виводить формули для гіпотенузи. Записує всі формули
д). Складаємо опорний конспект:
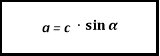

![]()
![]()
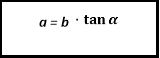

![]()
![]()
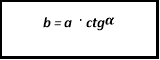


прилеглий b = c ![]()
катет
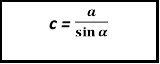

![]()
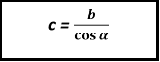
![]()
ІІІ. Первинне закріплення знань .
1.Дано ; с =10. , ![]() = 40
= 40![]() . Знайти а, в-?
. Знайти а, в-?
2. Дано : а = 8, ![]() = 70
= 70![]() Знайти: с -? а -?
Знайти: с -? а -?
ІV.Д/з №№ 721. Вивчити формули


про публікацію авторської розробки
Додати розробку
