Тема уроку « Застосування інтеграла до розв′язування задач»
Тема уроку « Застосування інтеграла до розв′язування задач»
Ванда Пашкова, учитель математики спеціалізованої школи -ІІІст. № 196, м. Київ
Мета уроку: систематизувати й узагальнити знання учнів з теми «Інтеграл та його застосування», формувати в учнів уміння та навички творчого застосування знань і вмінь до розвязування задач із застосуванням інтеграла; поглиблювати й розширювати діапазон знань з теми; виховувати відповідальне ставлення до навчання, культуру математичних обчислень та записів, учити учнів самостійно працювати над завданнями.
Тип уроку: узагальнення та систематизація знань.
Хід уроку
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
Перевірити правильність виконання домашніх завдань за записами, заготовленими на слайдах.
ІІІ. Мотивація навчальної діяльності.
Iv. Акуалізація опорних знань.
Метод «Мікрофон»
( представники кожної команди ставлять по черзі запитання учням інших команд. Якщо учні команди не відповідають на поставлене запитання, або дають неправильну відповідь,то запитання адресується учням інших команд).
- Яку функцію називають первісною функціїf на проміжкуI?
- Сформулювати основну властивість первісної.
- Який запис називають загальним виглядом первісних?
- Хто з математиків відкрив інтегральне числення?.
- Які є правила знаходження первісних?
- Дати означення криволінійної трапеції.
- За якою формулою можна обчислити площу криволінійної трапеції?
- Назвати властивості визначеного інтеграла
- В чому полягає геометричний зміст визначеного інтеграла?.
Завдання.Знайти первісну функції:
- f(x) = -3x+4
-
f(x) = 4
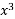 +2x +7;
+2x +7;
-
f(x) =
 +5
+5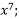
-
f(x) =
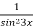 ;
;
-
f(x) = sin
 + 3;
+ 3;
- f(x) = cos7x;
-
f(x) =
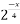 ;
;
- f(x) = sin7x∙cos7x;
-
f(x) =
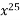 +
+  ;
;
-
f(x) =2∙
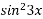
Відповіді: 1) F(x) = -![]() +4x+c; 2) F(x) =
+4x+c; 2) F(x) = ![]() +
+![]() +c; 3) F(x) =
+c; 3) F(x) =![]() +
+ ![]() +c; 4) F(x) =
+c; 4) F(x) =![]() tg3x +c;
tg3x +c;
5) F(x) =-9cos![]() +3x+c; 6) F(x) =
+3x+c; 6) F(x) =![]() sin7x+c; 7) F(x) =-
sin7x+c; 7) F(x) =-![]() +c; 8)
+c; 8)![]() ) F(x) = -
) F(x) = - ![]() cos14x +c; 9) ) F(x) =
cos14x +c; 9) ) F(x) =![]() -
- ![]() +c;
+c;
10) ) F(x) =x-![]() sin6x+c.
sin6x+c.
Чотири учні розв′язують наступні завдання біля дошки:
-
Знайти первісну функції f(x) =
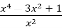 ,графік якої проходить через точку А(2;3)
,графік якої проходить через точку А(2;3)
Розв′язування.
f(x) =![]() -3 +
-3 + ![]()
F(x)= ![]() - 3x -
- 3x - ![]() + c,
+ c,
![]() -6 -
-6 - ![]() + c = 3 ;
+ c = 3 ;
![]() .
.
![]() - 3x -
- 3x - ![]() +
+ ![]() .
.
![]() :
:![]() - 3x -
- 3x - ![]() +
+ ![]() .
.
-
1)Знайти
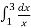
![]() = |lnx|
= |lnx|![]() = ln3-ln1=ln3
= ln3-ln1=ln3![]() 1,1
1,1
2). Обчислити: ![]() .
.
![]() .
.
-
Знайти первісну для функції f(x) = 4
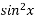 , графік якої проходить через точку А(
, графік якої проходить через точку А( ; 2).
; 2).
f(x) = 4∙![]() = 2 (1 – cos2x) = 2-2cos2x,
= 2 (1 – cos2x) = 2-2cos2x,
F(x)= 2x - 2![]() +c= 2x – sin2x +c.
+c= 2x – sin2x +c.
2∙![]() – sin
– sin![]() +c =2; c=2-
+c =2; c=2-![]() ;
; ![]() 2x – sin2x +2 –
2x – sin2x +2 –![]() .
.
![]()
![]() 2x – sin2x +2 –
2x – sin2x +2 –![]() .
.
-
Обчислити:
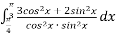 .
.
![]() = ( -3ctgx + 2tgx)|
= ( -3ctgx + 2tgx)| ![]() =
= ![]() + 1
+ 1 ![]() 2,7.
2,7.
![]() + 1
+ 1 ![]() 2,7.
2,7.
![]() .
.
![]() .
.
![]() язування завдань. Представник кожної команди розв’язує на дошці одне із завдань.
язування завдань. Представник кожної команди розв’язує на дошці одне із завдань.
![]()
-
Знайти загальний вигляд первісної для функції f(x) =
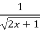 - sin
- sin .
.
2.Обчислити площу фігури, обмеженої лініями: y=![]() і 2x- y +3=0.
і 2x- y +3=0.
Відповіді: 1. ![]()
![]() - 4cos
- 4cos![]() +c. 2. 10
+c. 2. 10![]() .
.
![]()
- Довести тотожність.
![]() =
= ![]()
![]() =
=![]() =
= ![]() = 3.
= 3. ![]() =3.
=3.
Твердження доведено.
-
Знайти площу фігури, обмеженої лініями: y=
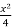 – 4; х=-3; х=8; у=0.
– 4; х=-3; х=8; у=0.
Відповідь: 41![]() .
.
![]()
1.Матеріальна точка рухається прямолінійно за законом: S(t) = ![]() +
+ ![]() -2t.
-2t.
Довести, що в момент часу t=![]() швидкість точки дорівнює 0.
швидкість точки дорівнює 0.
Доведення.
S′(t) =V(t) = ![]() +
+ ![]() -2.
-2.
Знайдемо інтеграл: t=1.
V(1) =1+1-2=0.
Відповідь:0.
![]()
-
Для функції f(x)=cos
 +
+ 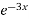 знайти первісну, графік якої проходить через точку А(0;3).
знайти первісну, графік якої проходить через точку А(0;3).
-
Обчислити інтеграл
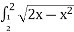 dx.
dx.
Відповіді: 1. ![]() 2sin
2sin![]() -
- ![]() : 2.
: 2. ![]() +
+ ![]() .
.
v.Підбиття підсумків уроку, рефлексія.
vІ. Домашнє завдання.
- Завдання за підручником.
- Додаткове завдання
- Обчислити площу фігури. Обмежену лініями:
У= ![]() |
| ![]() - 4|; у= 7 - | х|.
- 4|; у= 7 - | х|.
Відповідь:32.


про публікацію авторської розробки
Додати розробку
