Тематичне оцінювання з математики. 9 клас.
Тематичне
оцінювання
з математики
9 клас
9 клас (алгебра)
ТО №1. “Лінійні нерівності”.
І варіант
І рівень
1. Зобразити на числовому проміжку розв 'язки нерівності ![]() .
.
2. Відомо, що ![]() . Поставити замість * знак нерівності:
. Поставити замість * знак нерівності: ![]() *
* ![]() .
.
II рівень
3. Розв'язати нерівності:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
ІІІ рівень
4. Яке найбільше натуральне значення змінної b задовольняє нерівність
![]() .
.
5. При яких значеннях змінної х має зміст вираз ![]() .
.
IV рівень
6. Знайти розв'язок нерівності
![]() .
.
ІІ варіант
І рівень
1. Зобразити на числовому проміжку розв 'язки нерівності ![]() .
.
-
Відомо, що
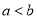 . Поставити замість * знак нерівності:
. Поставити замість * знак нерівності:
![]() *
* ![]() .
.
II рівень
3. Розв'язати нерівності:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
ІІІ рівень
4. Яке найменше ціле значення змінної у задовольняє нерівність
![]() .
.
5. При яких значеннях змінної х має зміст вираз ![]() .
.
IV рівень
6. Знайти розв'язок нерівності
![]() .
.
ІІІ варіант
І рівень
1. Зобразити на числовому проміжку розв 'язки нерівності ![]() .
.
2. Відомо, що ![]() . Поставити замість * знак нерівності:
. Поставити замість * знак нерівності: ![]() *
* ![]() .
.
II рівень
3. Розв'язати нерівності:
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
ІІІ рівень
4. Яке найбільше ціле значення змінної р задовольняє нерівність
![]() .
.
5. При яких значеннях змінної х має зміст вираз ![]() .
.
IV рівень
6. Знайти розв'язок нерівності
![]() .
.
ІV варіант
І рівень
1. Зобразити на числовому проміжку розв 'язки нерівності ![]() .
.
-
Відомо, що
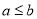 . Поставити замість * знак нерівності:
. Поставити замість * знак нерівності:
![]() *
* ![]() .
.
II рівень
3. Розв'язати нерівності:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
ІІІ рівень
4. Яке найменше ціле значення змінної у задовольняє нерівність
![]() .
.
5. При яких значеннях змінної х має зміст вираз ![]() .
.
IV рівень
- Знайти розв'язок нерівності
![]() .
.
ТО № 2. “Системи лінійних нерівностей”.
І варіант
І рівень
-
Зобразіть на координатній прямій проміжок
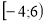 .
.
-
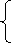 Знайдіть розв'язок системи нерівностей
Знайдіть розв'язок системи нерівностей 
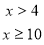
П рівень
![]()
![]() 3. Розв'яжіть систему нерівностей:
3. Розв'яжіть систему нерівностей:
а) ![]() б)
б) ![]()
4. Знайти цілі розв'язки системи нерівностей:
![]()
![]() .
.
ІІІ рівень
5. Знайти розв'язок системи нерівностей:
![]()
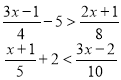
6. При яких значеннях х має зміст вираз ![]() .
.
IV рівень
7. Розв'яжіть подвійну нерівність
![]()
![]() .
.
8. Розв'яжіть нерівність ![]() .
.
ІІ варіант
І рівень
-
Зобразіть на координатній прямій проміжок
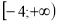 .
.
-
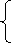 Знайдіть розв'язок системи нерівностей
Знайдіть розв'язок системи нерівностей 
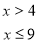
П рівень
![]()
![]() 3. Розв'яжіть систему нерівностей:
3. Розв'яжіть систему нерівностей:
а) ![]() б)
б) ![]()
4. Знайти цілі розв'язки системи нерівностей:
![]()
![]() .
.
ІІІ рівень
5. Знайти розв'язок системи нерівностей:
![]()
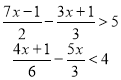
6. При яких значеннях х має зміст вираз ![]() .
.
IV рівень
7. Розв'яжіть подвійну нерівність
![]()
![]() .
.
8. Розв'яжіть нерівність ![]() .
.
ІІІ варіант
І рівень
1. Зобразіть на координатній прямій проміжок ![]() .
.
![]() 2. Знайдіть розв'язок системи нерівностей
2. Знайдіть розв'язок системи нерівностей ![]()
![]()
П рівень
![]()
![]() 3. Розв'яжіть систему нерівностей:
3. Розв'яжіть систему нерівностей:
а) ![]() б)
б) ![]()
4. Знайти цілі розв'язки системи нерівностей:
![]()
![]() .
.
ІІІ рівень
5. Знайти розв'язок системи нерівностей:
![]()
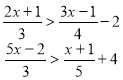
6. При яких значеннях х має зміст вираз ![]() .
.
IV рівень
7. Розв'яжіть подвійну нерівність
![]()
![]() .
.
8. Розв'яжіть нерівність ![]() .
.
ІV варіант
І рівень
![]() 1. Зобразіть на координатній прямій проміжок
1. Зобразіть на координатній прямій проміжок ![]() .
.
2. Знайдіть розв'язок системи нерівностей ![]()
![]()
П рівень
![]()
![]() 3. Розв'яжіть систему нерівностей:
3. Розв'яжіть систему нерівностей:
а) ![]() б)
б) ![]()
4. Знайти цілі розв'язки системи нерівностей:
![]()
![]() .
.
ІІІ рівень
5. Знайти розв'язок системи нерівностей:
![]()
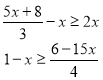
6. При яких значеннях х має зміст вираз ![]() .
.
IV рівень
7. Розв'яжіть подвійну нерівність
![]()
![]() .
.
8. Розв'яжіть нерівність ![]() .
.
ТО № 4. “Квадратична функція. Нерівності дутого степеня.”
І варіант
І рівень
1. Яка Функція називається квадратичною?
2. Графік якої функції схематично зображений на малюнку 1?
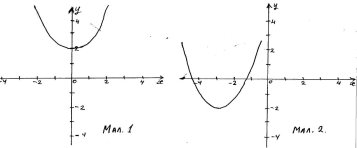 3. Вказати проміжок зростання функції, зображеної на малюнку 2.
3. Вказати проміжок зростання функції, зображеної на малюнку 2.
ІІ рівень
-
Знайти нулі функції
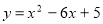 .
.
5. Побудувати графік функції ![]() за допомогою шаблона.
за допомогою шаблона.
6. Знайти координати вершини параболи ![]() .
.
ІІІ рівень
7. Знайти область значень функції ![]() .
.
8. Розв’язати нерівність ![]() .
.
VI рівень
9. Знайти область визначення функції
![]() .
.
ІІ варіант
 І рівень
І рівень
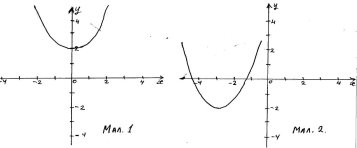
1. Де квадратична функція набуває від'ємних значень?
2. Графік якої функції схематично зображений на малюнку 1 ?
3. Вказати проміжок зростання функції, зображеної малюнку 2.
II рівень
4. Знайти нулі функції ![]() .
.
5. Побудувати графік функції ![]() за допомогою шаблона.
за допомогою шаблона.
6. Знайти координати вершини параболи ![]() .
.
ІІІ рівень
7. Знайти область значень функції ![]() .
.
8. Розв’язати нерівність ![]() .
.
VI рівень
9. Знайти область визначення функції
![]() .
.
ІІІ варіант
І рівень
1. За якою формулою обчислюється абсциса вершини параболи?
2. Графік якої функції схематично зображений на малюнку 1
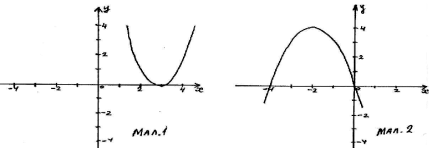
3. Вказати проміжок спадання функції, зображеної на малюнку 2.
II рівень
4. Знайти нулі функції ![]() .
.
5. Побудувати графік функції ![]() за
за
допомогою шаблона.
6. Знайти координати вершини параболи
![]() .
.
ІІІ рівень
7. Знайти проміжки зростання і спадання функції
![]() .
.
-
Розв'язати нерівність
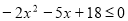 .
.
VI рівень - Знайти область визначення функції
![]()
IV варіант
І рівень
1. Де квадратична функція набуває додатних значень?
2. Графік якої функції схематично зображений на малюнку 1 ?
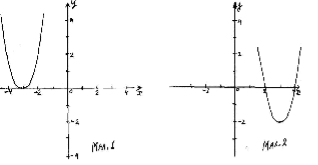
3. Вказати проміжок спадання функції, зображеної на малюнку 2.
II рівень
4. Знайти нулі функції ![]() .
.
5. Побудувати графік функції ![]() за допомогою шаблона.
за допомогою шаблона.
6. Знайти координати вершини параболи ![]() .
.
ІІІ рівень
7. Знайти проміжки зростання і спадання функції
![]() .
.
8. Розв'язати нерівність ![]() .
.
VI рівень
9. Знайти область визначення функції
![]()
ТО № 5. „Система рівнянь другого степеня”.
І варіант
І рівень
1. Чи є пара чисел (3; 5) розв'язком системи
![]()
![]() .
.
ІІ рівень
2. Розв'язати систему рівнянь
![]()
![]() .
.
3. Різниця двох чисел 4, а їх добуток 165. Знайти ці числа.
ІІІ рівень
4. Знайти розв'язки системи:
![]()
![]()
IV рівень
5. Знайти сторони прямокутної ділянки, якщо її площа 35 м2, периметр 24 м.
![]() 6. Розв'язати систему рівнянь:
6. Розв'язати систему рівнянь:
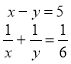
ІІ варіант
І рівень
1. Чи є пара чисел (2; 6) розв'язком системи
![]()
![]() .
.
ІІ рівень
2. Розв'язати систему рівнянь
![]()
![]() .
.
3. Сума двох чисел 15, а їх добуток 50. Знайти ці числа.
ІІІ рівень
4. Знайти розв'язки системи:
![]()
![]()
IV рівень
5. Один з катетів прямокутного трикутника на 3 см більший від другого. Знайти катети, якщо гіпотенуза 15 см.
6. Розв'язати систему рівнянь:
![]()
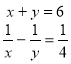
ІІІ варіант
І рівень
1. Чи є пара чисел (1; 4) розв'язком системи
![]()
![]() .
.
ІІ рівень
2. Розв'язати систему рівнянь
![]()
![]() .
.
3. Різниця двох чисел 1, а їх добуток 42. Знайти ці числа.
ІІІ рівень
4. Знайти розв'язки системи:
![]()
![]()
IV рівень
5. Одна сторона прямокутника більша за другу на 15 см. Знайти сторони прямокутника, якщо його площа 700 см2.
6. Розв'язати систему рівнянь:
![]()
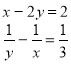
ІV варіант
І рівень
1. Чи є пара чисел (7; 5) розв'язком системи
![]()
![]() .
.
ІІ рівень
2. Розв'язати систему рівнянь
![]()
![]() .
.
3. Різниця двох чисел 11, а їх добуток 126. Знайти ці числа.
ІІІ рівень
4. Знайти розв'язки системи:
![]()
![]()
IV рівень
5. Знайти сторони прямокутника, якщо його площа 104 м2, а периметр 42 м.
6. Розв'язати систему рівнянь:
![]()
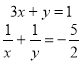
ТО № 7. “Числові послідовності”.
І варіант
І рівень
- Що таке арифметична прогресія?
- Записати формулу n-го члена геометричної прогресії.
- (аn) – арифметична прогресія, в якій а1 = 6, d = 5. Знайти а4.
ІІ рівень
- Знайти сьомий член геометричної прогресії, якщо а1 = -5, q = 3.
- Знайти суму 54-х перших членів арифметичної прогресії (аn), якщо а1 = -24, а54 = -185.
ІІІ рівень
- Дванадцятий член арифметичної прогресії 54, а різниця 5. Знайти перший член.
- Знайти а1 геометричної прогресії (аn), якщо S3 = 18, q = 2.
IV рівень
- Знайти перший член і різницю арифметичної прогресії (bn), якщо b4 = 33, b15 = 88.
- Знайти суму всіх від’ємних членів арифметичної прогресії: -6,2; -5,9; -5,6; … .
ІІ варіант
І рівень
- Як знайти різницю арифметичної прогресії?
- Записати формулу суми n членів геометричної прогресії.
- (аn) – арифметична прогресія, в якій а1 = 4, d = 7. Знайти а6.
ІІ рівень
- Знайти шостий член геометричної прогресії, якщо а1 = -18, q = 2.
- Знайти суму 48-х перших членів арифметичної прогресії (аn), якщо а1 = -18, а48 = -104.
ІІІ рівень
- Тридцятий член арифметичної прогресії 40, а різниця 4. Знайти перший член.
- Знайти а1 геометричної прогресії (аn), якщо S3 = 39, q = 3.
IV рівень
- Знайти перший член і різницю арифметичної прогресії (bn), якщо b4 = 10, b13 = 64.
- Знайти суму всіх додатних членів арифметичної прогресії: 4,6; 4,2; 3,8; … .
ІІІ варіант
І рівень
- Що таке геометрична прогресія?
- Записати формулу n-го члена арифметичної прогресії.
- (bn) – геометрична прогресія, в якій b1 = 3, q = 4. Знайти b5.
ІІ рівень
- Знайти 28-й член арифметичної прогресії (аn), якщо а1 = 44, d = -6.
- Знайти суму шести перших членів геометричної прогресії (bn), якщо b1 = 4, q = 3.
ІІІ рівень
- Перший член арифметичної прогресії 4, а тринадцятий член 28. Знайти різницю.
- Знайти а1 геометричної прогресії (аn), якщо S4 = 80, q = 3.
IV рівень
- Знайти перший член і знаменник геометричної прогресії (аn), якщо а4 = 54, а7 = 1458.
- Знайти суму всіх від’ємних членів арифметичної прогресії: -5,2; -4,8; -4,4; … .
ІV варіант
І рівень
- Як знайти знаменник геометричної прогресії?
- Записати формулу суми n перших членів арифметичної прогресії.
- (bn) – геометрична прогресія, в якій b1 = 5, q = 2. Знайти b4.
ІІ рівень
- Знайти 19-й член арифметичної прогресії (xn), якщо x1 = 35, d = -8.
- Знайти суму п’яти перших членів геометричної прогресії (аn), якщо а1 = 5, q = 2.
ІІІ рівень
- Перший член арифметичної прогресії дорівнює -5, а десятий член 40. Знайти різницю.
- Знайти а1 геометричної прогресії (аn), якщо S4 = 140, q = 4.
IV рівень
- Знайти перший член і знаменник геометричної прогресії (аn), якщо а6 = 96, а9 = 768.
- Знайти суму всіх додатних членів арифметичної прогресії: 7,2; 6,6; 6; … .
ТО № 8. “Елементи прикладної математики”.
І варіант
І рівень
- Округлити число 2,3843 з точністю до сотих.
- Відомо, що х = 42,9 0,2. Записати це у вигляді подвійної нерівності.
- Перетворити 40%, 5% у дроби.
ІІ рівень
- Знайти число, 40% якого дорівнює 80.
- Знайти (з точним урахуванням похибок) суму і різницю наближених значень: а = 5,27 0,02, b = 1,14 0,03.
ІІІ рівень
-
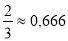 . Знайти абсолютну похибку.
. Знайти абсолютну похибку.
- Морська вода містить 6% солі. Скільки води потрібно взяти, щоб отримати 42 кг солі?
IV рівень
- Змішали 50% розчин кислоти з 10% і отримали 500 г 20% розчину. Скільки грамів кожного розчину було взято?
ІІ варіант
І рівень
- Округлити число 4,376 з точністю до сотих.
- Відомо, що у = 24,8 0,3. Записати це у вигляді подвійної нерівності.
- Перетворити 30%, 6% у дроби.
ІІ рівень
- Знайти 30% від числа 120.
- Знайти (з точним урахуванням похибок) суму і різницю наближених значень: а = 4,17 0,03, b = 2,35 0,01.
ІІІ рівень
-
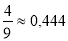 . Знайти абсолютну похибку.
. Знайти абсолютну похибку.
- Вкладник поклав до банку 20000 грн. під 5% річних. Скільки гривень буде в нього на рахунку через 2 роки?
IV рівень
- Змішали 35% розчин кислоти з 10% і отримали 300 г 20% розчину. Скільки грамів кожного розчину було взято?
ІІІ варіант
І рівень
- Округлити число 5,756 з точністю до десятих.
- Відомо, що а = 31,2 0,5. Записати це у вигляді подвійної нерівності.
- Перетворити 50%, 7% у дроби.
ІІ рівень
- Знайти 20% від числа 85.
- Знайти (з точним урахуванням похибок) суму і різницю наближених значень: а = 8,46 0,03, b = 3,24 0,01.
ІІІ рівень
-
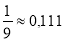 . Знайти абсолютну похибку.
. Знайти абсолютну похибку.
- Морська вода містить 4% солі. Скільки солі міститься в 320 г морської води?
IV рівень
- Змішали 30% і 10% розчини соляної кислоти і одержали 600 г 15% розчину. Скільки грамів кожного розчину було взято?
IV варіант
І рівень
- Округлити число 6,628 з точністю до десятих.
- Відомо, що b = 60,7 0,4. Записати це у вигляді подвійної нерівності.
- Перетворити 60%, 2% у дроби.
ІІ рівень
- Знайти число, 20% якого дорівнює 140.
- Знайти (з точним урахуванням похибок) суму і різницю наближених значень: а = 9,21 0,04, b = 5,36 0,03.
ІІІ рівень
-
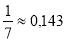 . Знайти абсолютну похибку.
. Знайти абсолютну похибку.
- Вкладник поклав до банку 10000 грн. під 4% річних. Скільки гривень буде в нього на рахунку через 2 роки?
IV рівень
- Змішали 30% і 60% розчини оцтової кислоти і отримали 750 г 44% розчину. Скільки грамів кожного розчину було взято?
Підсумкова контрольна робота
І варіант
І рівень
1. Розв'яжіть нерівність ![]()
2. Знайдіть різницю арифметичної прогресії (an), якщо a1 = 7, a2 = 16.
3. Обчисліть значення функції ![]() в точці
в точці ![]() .
.
ІІ рівень
4. При яких значеннях змінної має зміст вираз
![]() .
.
5. Розв'яжіть систему нерівностей
![]()
![]() .
.
ІІІ рівень
6. Чи належить точка А (-2; 10) графіку функції
![]() .
.
7. Розв'яжіть систему рівнянь
![]()
![]()
IV рівень
8. Відстань між двома містами дорівнює 420 км. З одного міста до іншого виїхали одночасно дві машини. Швидкість однієї з них на 10 км/год більша за швидкість другої, через що вона приїхала в пункт призначення на одну годину раніше від другої машини. Знайдіть швидкість кожної машини.
ІІ варіант
І рівень
1. Розв'яжіть нерівність ![]()
2. Знайдіть різницю арифметичної прогресії (an), якщо a1 = 8, a2 = 19.
3. Обчисліть значення функції ![]() в точці
в точці ![]() .
.
ІІ рівень
4. При яких значеннях змінної має зміст вираз
![]() .
.
5. Розв'яжіть систему нерівностей
![]()
![]() .
.
ІІІ рівень
6. Чи належить точка А (-2; 2) графіку функції
![]() .
.
7. Розв'яжіть систему рівнянь
![]()
![]()
IV рівень
8. З міста А до міста В, відстань між якими дорівнює 350 км, виїхали одночасно вантажна і легкова машини. Швидкість вантажівки на 20 км/год менша, ніж швидкість легкової машини, через що вона прибула до міста В на 2 год пізніше за легкову. Знайдіть швидкість кожної машини.
9клас (геометрія)
ТО № 1. “Декартові координати”.
І варіант
І рівень
- Записати загальне рівняння кола.
- Скласти рівняння кола з центром в точці О(4; 5), R = 5 см.
- А(1; -4), В(7; 6). Знайти середину відрізка АВ.
ІІ рівень
- С(2; 3), D(5; -1). Знайти довжину відрізка CD.
- Перевірити, чи точка D(-2; 1) належить прямій 2х + 3у – 4 = 0.
ІІІ рівень
- Знайти точку перетину прямої х + 2у – 5 = 0 з віссю х.
- Знайти довжину медіани ВК трикутника АВС з вершинами А(-3; 3), В(4; 1), С(2; 5).
IV рівень
- Скласти рівняння прямої, яка проходить через точки D(3; -4), S(0; -2).
- Знайти координати центра і радіус кола, заданого рівнянням х2 + у2 – 6х + 10у = 2.
ІІ варіант
І рівень
- Записати формули для обчислення середини відрізка.
- Скласти рівняння кола з центром в точці О(1; 5), R = 7 см.
- А(3; -7), В(9; 3). Знайти середину відрізка АВ.
ІІ рівень
- С(4; 13), D(-1; 1). Знайти довжину відрізка CD.
- Перевірити, чи точка С(2; 1) належить колу, рівняння якого (х + 2)2 + (у – 1)2 = 16.
ІІІ рівень
- Знайти точку перетину прямої 5х + у + 4 = 0 з віссю у.
- Знайти довжину медіани СК трикутника АВС з вершинами А(-2; 3), В(2; 1), С(3; 5).
IV рівень
- Скласти рівняння прямої, яка проходить через точки D(2; 0), S(3; -2).
- Знайти координати центра і радіус кола, заданого рівнянням х2 + у2 + 8х – 4у = 5.
ІІІ варіант
І рівень
- Записати загальне рівняння прямої.
- Скласти рівняння кола з центром в точці О(2; 3), R = 3 см.
- А(11; -1), В(3; 7). Знайти середину відрізка АВ.
ІІ рівень
- С(2; -1), D(10; -7). Знайти довжину відрізка CD.
- Перевірити, чи точка D(2; 1) належить прямій 3х + у – 7 = 0.
ІІІ рівень
- Знайти точку перетину прямої 5х + 2у – 10 = 0 з віссю х.
- Знайти довжину медіани АК трикутника АВС з вершинами А(0; -1), В(2; 1), С(-2; 3).
IV рівень
- Скласти рівняння прямої, яка проходить через точки D(0; 2), S(2; -1).
- Знайти координати центра і радіус кола, заданого рівнянням х2 + у2 – 2х – 8у = – 1.
IV варіант
І рівень
- Записати формулу для обчислення відстані між точками.
- Скласти рівняння кола з центром в точці О(4; 6), R = 2 см.
- А(-3; -6), В(-5; 8). Знайти середину відрізка АВ.
ІІ рівень
- С(0; 1), D(3; 5). Знайти довжину відрізка CD.
- Перевірити, чи точка С(1; 3) належить колу, рівняння якого (х + 4)2 + (у – 3)2 = 25.
ІІІ рівень
- Знайти точку перетину прямої 3х + 2у – 8 = 0 з віссю у.
- Знайти довжину медіани ВМ трикутника АВС з вершинами А(-3; 4), В(2; 1), С(3; -2).
IV рівень
- Скласти рівняння прямої, яка проходить через точки D(-1; -2),
S(0; 1).
- Знайти координати центра і радіус кола, заданого рівнянням х2 + у2 + 10х – 6у = 30.
ТО № 2. “Рухи і вектори на площині”.
І варіант
І рівень
- Рухом називається перетворення…
- Що таке вектор?
- Сумою векторів a i b називається.
ІІ рівень
- Дано точки А(1; 4), В(2; 7). Знайти вектор АВ.
- Паралельне перенесення задається формулами x′ = x + 4,
y′ = y – 7. В яку точку при цьому паралельному перенесенні
переходить точка М(–2; 8).
- Знайти абсолютну величину вектора а(–3; 4).
ІІІ рівень
- Точка К(–5; 8). Записати координати точки К′ симетричної точці К відносно початку кооддинат.
- Дано вектори а(–4; 5), b(2; –6). Знайти 3а + 2b.
IV рівень
- Знайти кут між векторами а і b, якщо а(0; 1), b(–1; 1).
- Знайти значення n, при якому вектори с(–3; n), d(10; –5), перпендикулярні.
ІІ варіант
І рівень
- Симетрією відносно точки називається…
- Що таке абсолютна величина вектора?
- Добутком вектора a на число λ називається.
ІІ рівень
- Дано точки А(0; 3), В(–3; 5). Знайти вектор АВ.
- Паралельне перенесення задається формулами x′ = x – 3, y′ = y + 5. В яку точку при цьому паралельному перенесенні переходить точка N(5; –7).
- Знайти абсолютну величину вектора а(–5; 12).
ІІІ рівень
- Точка M(4; –6). Записати координати точки M′ симетричної точці M відносно осі х.
- Дано вектори а(6; –1), b(3; –4). Знайти –5а + 3b.
IV рівень
- Знайти кут між векторами а і b, якщо а(2; 0), b(–3; –3).
- Знайти значення n, при якому вектори с(n; 2), d(–4; –10), перпендикулярні.
ІІІ варіант
І рівень
- Паралельним перенесенням називається …
- Які вектори називаються колінеарними?
- Вектори перпендикулярні, якщо…
ІІ рівень
- Дано точки А(5; 1), В(0; –3). Знайти вектор АВ.
- Паралельне перенесення задається формулами x′ = x – 1, y′ = y + 10. В яку точку при цьому паралельному перенесенні переходить точка F(6; –2).
- Знайти абсолютну величину вектора а(–4; 3).
ІІІ рівень
- Точка N(–9; 12). Записати координати точки N′ симетричної точці N відносно початку кооддинат.
- Дано вектори а(–5; 6), b(1; –9). Знайти –2а + 7b.
IV рівень
- Знайти кут між векторами а і b, якщо а(–2; 1), b(2; 4).
- Знайти значення n, при якому вектори с(n; 6), d( –10; 5), перпендикулярні.
IV варіант
І рівень
- Симетрією відносно прямої називається…
- Як знайти координати вектора?
- Скалярним добутком векторів a і b називається.
ІІ рівень
- Дано точки А(3; 6), В(–1; 8). Знайти вектор АВ.
- Паралельне перенесення задається формулами x′ = x + 2, y′ = y – 5. В яку точку при цьому паралельному перенесенні переходить точка D(4; –1).
- Знайти абсолютну величину вектора а(15; –8).
ІІІ рівень
- Точка M(3; –7). Записати координати точки M′ симетричної точці M відносно осі у.
- Дано вектори а(3; –2), b(7; 4). Знайти 4а – 2b.
IV рівень
- Знайти кут між векторами а і b, якщо а(0; 5), b(–5; –5).
- Знайти значення n, при якому вектори с(n; 2), d(1; –4), перпендикулярні.
ТО № 3. „Розв'язування трикутників”
І варіант
І рівень
- Загасати теорему косинусів для сторони а.
- Записати теорему синусів для сторін а і b і відповідних протилежних кутів.
- Продовжити речення:
у трикутнику проти більшої сторони...
ІІ рівень
- У трикутнику АВС: АВ = 15 см, ВС = 8 см, АС = 6 см. Який з кутів трикутника найменший?
- Діагоналі паралелограма дорівнюють 2 см і 6 см, а кут між ними 60. Знайти меншу сторону паралелограма.
ІІІ рівень
6) Дано сторону і два кути трикутника. Знайдіть третій кут та інші дві сторони, якщо а = 15 см, β = 46°, γ = 124°.
IV рівень
- У рівнобедреному трикутнику основа дорівнює 18 см, а кут при основі 38°. Знайдіть радіус описаного кола.
- В різнобічній трапеції діагональ утворює з більшою основою і бічною стороною кути 32° і 54°, менша основа трапеції дорівнює 10 см. Знайти сторони трапеції.
ІІ варіант
І рівень
- Записати теорему косинусів для сторони b.
- Записати теорему синусів для сторін b і с і відповідних протилежних кутів.
- Продовжити речення:
у трикутнику проти меншого кута...
ІІ рівень
-
У трикутнику АВС:
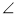 А = 60,
А = 60, 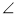 В = 20°,
В = 20°, 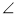 С = 100. Яка із сторін трикутника найбільша?
С = 100. Яка із сторін трикутника найбільша?
- Діагоналі паралелограма дорівнюють 10 см і 8 см, а кут між ними 120°. Знайти більшу сторону паралелограма.
ІІІ рівень
6) У трикутнику дано дві сторони і кут, протилежний до однієї з них. Знайдіть інші два кута і третю сторону трикутника, якщо а = 36 см, b = 15 см, α = 120.
- У рівнобедреному трикутнику основа дорівнює 22 см, а кут при основі 42°. Знайдіть радіус описаного кола.
- В рівнобічній трапеції гострий кут дорівнює 80°, а менша основа дорівнює бічній стороні. Знайти сторони трапеції, якщо більша основа дорівнює 12 см.
ТО № 4. “Многокутники”.
І варіант
І рівень
- Що таке опуклий многокутник?
- Який многокутник називається описаний навколо кола?
- За якою формулою обчислюється довжина кола?
ІІ рівень
- Знайти суму внутрішніх кутів опуклого 7-кутника.
-
Знайти радіус кола, описаного навколо правильного трикутника із стороною
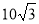 см.
см.
ІІІ рівень
- Скільки сторін у опуклого многокутника, якщо сума його внутрішніх кутів 1620°?
- У правильний чотирикутник зі стороною 8 см вписано коло. Знайти довжину кола.
IV рівень
- У рівнобедреному трикутнику бічна сторона 20 см, а основа дорівнює 32 см. знайти радіус кола, описаного навколо трикутника.
ІІ варіант
І рівень
- Що таке ламана?
- Який многокутник називається вписаний в коло?
- Яка формула радіуса кола, описаного навколо правильного трикутника?
ІІ рівень
- Знайти суму внутрішніх кутів опуклого 17-кутника.
-
Знайти радіус кола, вписаного у правильний трикутник із стороною
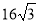 см.
см.
ІІІ рівень
- Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого 150°?
-
Периметр правильного трикутника
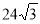 см. Обчислити довжину кола, описаного навколо цього трикутника.
см. Обчислити довжину кола, описаного навколо цього трикутника.
IV рівень
- Катети прямокутного трикутника відносяться як 3 : 4, а периметр дорівнює 36 см. Обчислити радіус кола, описаного навколо трикутника.
ІІІ варіант
І рівень
- Що таке многокутник?
- Який многокутник називається правильним?
- Яка формула радіуса кола, вписаного в квадрат?
ІІ рівень
- Знайти суму внутрішніх кутів опуклого 10-кутника.
-
Сторона правильного чотирикутника
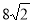 см. Знайти радіус кола, описаного навколо цього чотирикутника.
см. Знайти радіус кола, описаного навколо цього чотирикутника.
ІІІ рівень
- Скільки сторін має опуклий многокутник, якщо сума його внутрішніх кутів 3600°?
- Правильний чотирикутник зі стороною 12 см описаний навколо кола. Знайти сторону правильного чотирикутника, вписаного у дане коло.
IV рівень
- Довжина кола, описаного навколо рівнобедреного трикутника дорівнює 60 см. Обчислити периметр цього трикутника, якщо основа дорівнює 48 см.
IV варіант
І рівень
- Що таке кут многокутника?
- Яка формула суми кутів опуклого многокутника?
- Яка формула радіуса кола, вписаного в шестикутник?
ІІ рівень
- Знайти суму внутрішніх кутів опуклого 8-кутника.
-
Знайти радіус кола, описаного навколо правильного трикутника із стороною
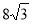 см.
см.
ІІІ рівень
- Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого 144°?
- Периметр правильного трикутника 12 см. Обчислити довжину кола, описаного навколо цього трикутника.
IV рівень
- У прямокутному трикутнику катети дорівнюють 9 см і 12 см. Знайти радіус кола, вписаного в трикутник.
Річна контрольна робота
І варіант
І рівень
- Який многокутник називається вписаним в коло?
- Записати теорему косинусів для сторони с.
- Обчислити площу трикутника, сторона якого 8 см, а висота, опущена на неї, 5 см.
ІІ рівень
- Знайти суму внутрішніх кутів опуклого восьмикутника.
-
Знайти радіус кола, описаного навколо правильного трикутника зі стороною
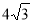 см.
см.
ІІІ рівень
- Сторони трикутника дорівнюють 12 см, 13 см, 15 см. Знайти сторони подібного трикутника, у якого сума найменшої і найбільшої сторін 54 см.
- Периметр рівнобедреного трикутника дорівнює 128 см, а бічна сторона 40 см. Обчислити радіус вписаного кола.
IV рівень
- Різниця основ прямокутної трапеції дорівнює 7 см, а менша діагональ є бісектрисою прямого кута. Обчислити площу трапеції, якщо її більша бічна сторона 25 см.
ІІ варіант
І рівень
- Який многокутник називається описаним навколо кола?
- Записати теорему косинусів для сторони b.
- Обчислити площу паралелограма, сторона якого 7 см, а висота, опущена на неї, 4 см.
ІІ рівень
- Знайти суму внутрішніх кутів опуклого десятикутника.
-
Знайти радіус кола, вписаного в правильний трикутник із стороною
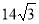 см.
см.
ІІІ рівень
- Сторони трикутника дорівнюють 12 см, 13 см, 15 см. Знайти сторони подібного трикутника, у якого різниця найбільшої і найменшої сторін 9 см.
- Периметр рівнобедреного трикутника дорівнює 128 см, а бічна сторона 40 см. Обчислити радіус описаного кола.
IV рівень
- Різниця основ прямокутної трапеції дорівнює 7 см, а більша діагональ є бісектрисою прямого кута. Обчислити площу трапеції, якщо її більша бічна сторона 25 см.


про публікацію авторської розробки
Додати розробку
