Теорема Піка та її практичне застосування

        Міністерство освіти і науки України
 Управління освіти і науки Чернігівської облдержадміністрації
 Обласний комунальний позашкільний навчальний заклад

«Чернігівська Мала академія наук учнівської молоді»

Чернігівської обласної ради

                                                                       Відділення:  наук про Землю

                                                                     Секція: геоінформаційні системи та

                                                            дистанційне зондування Землі

ТЕОРЕМА ПІКА ТА ЇЇ ПРАКТИЧНЕ ЗАСТОСУВАННЯ

Роботу виконала:

Грищенко Ірина Олександрівна,

учениця 10 класу Деснянського ліцею Деснянської селищної ради

Науковий керівник:

Коваль Наталія Петрівна,

учитель математики Деснянського ліцею Деснянської селищної ради

Чернігів – 2022

                               Анотація до науково-дослідної роботи

«Теорема Піка та її практичне застосування»

учениці 10 класу Деснянського ліцею Деснянської селищної ради Грищенко Ірини Олександрівни, Чернігівське територіальне відділення Малої академії наук України.

Науковий керівник: учитель математики  вищої кваліфікаційної категорії, «старший учитель» Коваль Наталія Петрівна.

           Актуальність вибраної теми полягає у використанні теореми Піка для аналізу даних дистанційного зондування Землі, визначення  площі географічного об’єкту, зображеного на супутниковому знімку та  на дрібномасштабній географічній карті, земельної ділянки, зображеної на плані. Цім самим ілюструючи практичне застосування геометрії.

У ході роботи було проведено ряд досліджень, а саме:

1. Експериментальним  шляхом було підтверджено справедливість формули Піка для обчислення площі багатокутника та круга.

2. Виконано дослідження ефективності застосування теореми Піка для обчислення площі території, зображеної на дрібномасштабній географічній карті, та на супутниковому знімку, земельної ділянки, зображеної на плані.

Результати дослідження показали:

1. Площа фігури, обчислена за теоремою Піка,  дорівнює площі фігури, обчисленої за формулою планіметрії для багатокутників.

2. Площу географічного об’єкта, зображеного на дрібномасштабній географічній карті, та на супутниковому знімку, за теоремою Піка визначити набагато простіше, але отримані значення будуть наближені до дійсних, точність обчислень залежить від величини масштабу і кривизни границі об'єкта. Середня похибка обчислень становить 5,9%. Обчислення площі земельної ділянки, зображеної на плані, дає точне значення.

Ключові слова: площа, теорема Піка, географічний об’єкт, супутниковий знімок, географічна карта, план.

ЗМІСТ

ВСТУП ……………………………………………………………...............  4 – 7

РОЗДІЛ 1 

Теоретичні відомості

1.           Дистанційне зондування землі…………………………………… 8 – 9   Поняття про вимірювання ………………………………………….   9  
2.           Вимірювання площі …………………………………………………  9

РОЗДІЛ 2 

Методи обчислення площі фігури неправильної геометричної

форми ……………………………………………………………………...  10 – 12

РОЗДІЛ 3

Дослідження площ геометричних фігур

2.1. Обчислення площі багатокутника ……………………….…………..13 – 18

2.2. Обчислення площі круга та його частин …………….…….............. 18 – 21

2.3.  Експеримент і дослідження ………………………………………… 22 – 25

ВИСНОВКИ ………………………………………………………............. 26 – 27 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ …………………………...........  28

ДОДАТКИ ………………………………………………………………… 29 – 32

ВСТУП

Кращий спосіб вивчити що-небудь – це відкрити самому.

Д. Пой

Геометрія володіє цілим рядом якостей, має у своєму розпорядженні величезні можливості для емоційного та духовного розвитку людини. «Я думаю, що ніколи до теперішнього часу ми не жили в такий геометричний період. Все навколо – геометрія». Ці слова великого французького архітектора Корбюз’є дуже точно характеризують наш час. Світ, у якому ми живемо, наповнений геометрією будинків і вулиць, гір і полів, творіннями природи й людини. Краще орієнтуватися в ньому, відкривати нове, розуміти красу й мудрість навколишнього світу нам допомагає геометрія.

Геометрія зародилася в далекій давнині. Будуючи будинки та храми, прикрашаючи їх орнаментами, вимірюючи відстані й площі, людина застосовувала свої знання про форму, розміри та взаємне розташування предметів, отримані зі спостережень і дослідів. Майже всі великі вчені давнини та середньовіччя були видатними геометрами. Давньогрецький філософ Платон, який проводив бесіди зі своїми учнями, одним з девізів своєї школи проголосив: «Не знаючі геометрії  не допускаються!»

Однією зі сфер застосування геометрії є використання її методів для визначення площ різноманітних фігур. Обчислення площі фігури є однією із задач, яка ілюструє практичне застосування геометрії, та однією з найдавніших задач, яку почали розв’язувати ще в давнину.

У звичайному житті на кожному кроці ми зустрічаємося з поняттям "площа". Що таке "площа", знає кожен. Кожен розуміє сенс слів: площа кімнати, площа будинку, площа земельної ділянки. Вимірювання площ вважають одним з найдавніших розділів геометрії; зокрема,  назву "геометрія" (тобто "земле- вимір") пов'язують саме з вимірюванням площі земельної ділянки.

Площа – найважливіша характеристика земельної ділянки. Визначення площі земельної ділянки на планах і картах має велике значення під час аналізу дистанційного зондування Землі, складання кадастрових планів сільськогосподарських угідь, в екології, лісовпорядкуванні, геології.

Найточнішим методом визначення площ є аналітичний метод, коли площу визначають за координатами контурних точок. Точність визначення площі у цьому випадку залежить від точності визначення координат і кількості контурних точок. Відносна помилка аналітичного методу становить приблизно 0,1 %. Так визначають площі переважно на електронних картах. На паперових носіях площі визначають графічним методом. При використанні графічного методу, коли ділянку поділяють на прості геометричні фігури (трикутники, трапеції), і площу кожної ділянки обчислюють за відомими геометричними формулами, відносна похибка визначення площі становить 1-2 %. При визначенні площ ділянок, обмежених криволінійним контуром на плані, площі визначають за допомогою планіметра з відносною похибкою 1-2 % або з допомогою палеток.

З вищесказаного зрозуміло, що обчислення площі -  дуже складний і тривалий процес, однак у деяких випадках бажано оцінити площу географічного об’єкта більш простим способом.

При вивченні цього питання ми звернули увагу на теорему Піка. У 1899 році австрійський математик Георг Пік довів теорему, яка дає просту формулу для обчислення площі фігури неправильної форми. Широку відомість теорема отримала в 1969 році після того, як Гуго Штейнгауз включив її у свою знамениту книгу «Математичний калейдоскоп».

        У процесі виконання роботи ми дослідили задачі по знаходженню площі довільної фігури за допомогою теореми Піка та оцінили практичне використання теореми для знаходження площі географічного об’єкта, зображеного на супутниковому знімку, дрібномасштабній географічній карті та земельної ділянки, зображеної на плані.

Об’єкт дослідження: геометричні фігури, географічні об’єкти зображені на дрібномасштабної географічної карті, та на супутниковому знімку,  земельні ділянки, зображені на плані.

Предмет дослідження: теорема Піка.

Гіпотеза: площу географічного об’єкта, зображеного на дрібномасштабної географічної карті та на супутниковому знімку,    земельної ділянки, зображеної на плані можна обчислити за допомогою теореми Піка.

Мета роботи:

•      експериментальним  шляхом упевнитися в справедливості теореми Піка.

•    дослідити ефективність застосування теореми Піка для обчислення площі географічного об’єкта,  зображеного на дрібномасштабній географічній карті та на супутниковому знімку,  земельної ділянки, зображеної на плані.

 Відповідно до мети  визначено такі основні завдання:

•    розширити знання про різноманіття задач на обчислення площі геометричної фігури за теоремою Піка у порівнянні з формулами планіметрії;

•    обґрунтувати раціональність використання теореми Піка для аналізу даних дистанційного зондування Землі, обчисленні площі географічного об’єкта, зображеного на дрібномасштабній географічній карті та на супутниковому знімку, земельної ділянки, зображеної на плані.

 Наукова новизна роботи полягає в тому, що вперше теорема Піка використовується для аналізу даних дистанційного зондування Землі, обчислення площі географічного об’єкта зображеного на супутниковому знімку; вперше для знаходженні вузлів решітки, потрібних для використання теореми Піка,  використовується палетка й виведена формула, яка дає можливість отримувати відповідь з урахуванням масштабу  у квадратних кілометрах  для географічного об’єкта, зображеного на дрібномасштабній географічній карті,  та земельної ділянки, зображеної на плані.

Практичне значення: результати досліджень дають можливість рекомендувати теорему Піка для вивчення в школі. Теорема Піка має значну пізнавальну і практичну цінність.

Методи дослідження: для виконання завдань дослідження використано аналіз науково-педагогічних джерел, моделювання, порівняння, систематизацію, узагальнення, аналіз.

РОЗДІЛ 1. ТЕОРЕТИЧНІ ВІДОМОСТІ

1.   Дистанційне зондування землі

      Дистанційне зондування Землі – це спостереження нашої планети за допомогою знімальних пристроїв, встановлених на космічних апаратах та інших літальних об’єктах, яке дає змогу фіксувати зміни та визначати тенденції процесів, що відбуваються на поверхні Землі й над нею. Космічні знімки подібні до звичайних фотографій, але відображають Землю в різних спектральних діапазонах.

           Дистанційне зондування Землі використовується надзвичайно широко: за його допомогою відстежують, природну й антропогенну трансформацію екосистем і перебіг та наслідки надзвичайних ситуацій. Місце й обсяг вирубки лісів і зелених насаджень, зміни русла ріки, масштаби пожежі при займанні торфовищ, обсяг розливу нафтопродуктів – все це й чимало іншого дають змогу визначити й оцінити саме космічні знімки. Однак найцікавіше й чи не найважливіше є можливість простежувати будь-які зміни в динаміці. Дистанційне зондування Землі є незамінним для огляду важкодоступних або небезпечних ділянок, наприклад території Зони відчуження навколо Чорнобильської АЕС.

           Супутникові знімки робляться доволі часто і регулярно, тому інформація, отримана таким чином, завжди є актуальною та достовірною. Також дуже важливим аспектом є багатоспектральний характер спостережень, так як супутники можуть робити знімки в різних діапазонах спектру, що дозволяє нам бачити планету більш широко, ніж можемо власним оком, а також аналізувати й відстежувати будь-яке явище, що трапляється на Землі.

           Існує величезна кількість онлайн-джерел, в яких звичайний користувач може безкоштовно отримати супутникові знімки середньої та навіть високої якості. Такі інтернет-платформи як EO Browser та Google Earth надають нам можливість спостерігати поверхню нашої планети «очима» наших супутників .

2. Поняття про вимірювання

          Вимірювання - це порівняння з деяким еталоном.

          Метою вимірювання є встановити, яка кількість еталонних зразків можна помістити в вимірюваному об'єкті .  Ця кількісна характеристика і є результатом вимірювання, а еталон стає одиницею виміру. Чим дрібніші похідні основного еталона використовуються у вимірах, тим вища точність вимірювання. На практиці точність будь-яких вимірювань обмежена можливостями вимірювальної апаратури.

3.  Вимірювання площ

           Існує нескінченна кількість плоских фігур різної форми - як правильних, так і неправильних. Загальною властивістю всіх фігур є те, що будь-яка з них має площу. .  

            Площі фігур - це розміри частини площині, займаної цими фігурами, виражені в певних одиницях. Величина площі завжди виражена додатнім числом. Одиницею вимірювання служить площа квадрата, сторона якого дорівнює одиниці довжини .  

           Площі простих геометричних фігур (прямокутників, трикутників, паралелограмів, трапеції, круга) зазвичай визначають за допомогою вимірювань: спочатку вимірюють лінійні розміри фігури (довжину, висоту, ширину, радіус), а потім обчислюють площу, користуючись відповідними математичними формулами. .  

Для визначення площі фігури неправильної  геометричної форми застосовують спеціальні методи.

РОЗДІЛ 2. МЕТОДИ ОБЧИСЛЕННЯ ПЛОЩІ ФІГУРИ НЕПРАВИЛЬНОЇ ГЕОМЕТРИЧНОЇ ФОРМИ

Збільшення обсягу знань, їх систематизація та узагальнення сприяли розробці різних методів знаходження площі фігури неправильної геометричної форми. Наведемо приклади деяких з них.

1.  Метод сум

Фігура неправильної геометричної форми поділяється на прості геометричні фігури, у результаті площа шуканої фігури знаходиться як сума площ її частин: S_ф = S₁ + S₂ + S₃ + S₄  

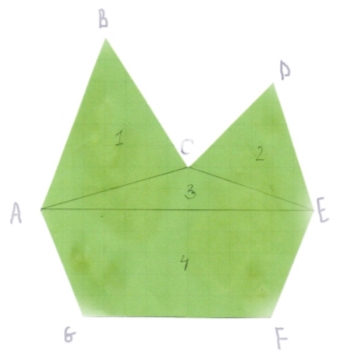
Рис. 1.1

2. Обчислення площі палеткою.

Палетка — прозора пластина з нанесеною на неї сіткою квадратів певної площі

Площу фігури неправильної геометричної форми даним методом обчислюють за формулою:  S = ٠S₁, де

А – кількість квадратів,  які цілком містяться у фігурі;

В – кількість квадратів,  які частково містяться  у фігурі,

S₁ – площа одного квадрата.

Рис. 1.2

3. Метод доповнення

Для обчислення площі фігури неправильної геометричної форми даним методом потрібно добудувати її до прямокутника, обчислити площі простих геометричних фігур, які доповнюють  багатокутник до прямокутника, і відняти суму знайдених площ   від площі прямокутника. 

S_ф = S_{прямокутника} – ( S₁ + S₂ + S₃ + S₄ + S₅)

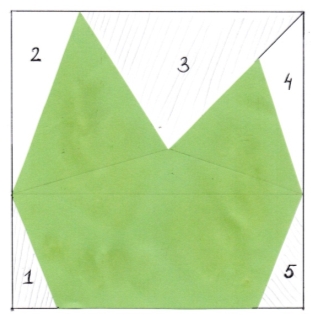
Рис. 1.3

4. Теорема Піка

Для застосування теореми слід накласти на фігуру неправильної геометричної форми палетку з розміром клітини 1 см на 1 см,  знайти кількість вузлів решітки, які потрапили всередину фігури (В), кількість вузлів решітки, які потрапили на границю фігури (Г).

Обчислити площу фігури за формулою: S = В + – 1.

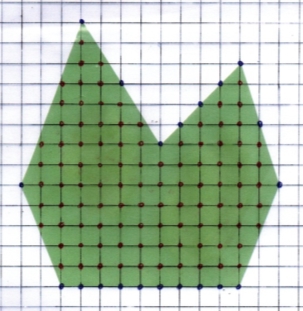
    Рис.  1.4

РОЗДІЛ 3. ДОСЛІДЖЕННЯ ПЛОЩ ГЕОМЕТРИЧНИХ ФІГУР

1.                Обчислення площі багатокутника

Обчислимо площу багатокутників  за допомогою формул  планіметрії та за допомогою теореми Піка та порівняємо отримані результати.

Задача 1. Обчислити площу прямокутника зі сторонами 9 см і 6 см.

Розв’язання:

За формулами планіметрії

Рис.2.1

АВСD – прямокутник, АВ = 9 см, ВС = 6 см, S_ABCD = АВ ВС=  54 (см²)

Відповідь: 54 cм²

За теоремою Піка

Рис.2.2

Розмістивши на прямокутнику палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину прямокутника (В), кількість вузлів решітки, які потрапили на границю прямокутника (Г).

Обчислимо площу прямокутника за формулою: S = В + – 1.

В =  40,    Г = 30,     S = В + – 1 =  40 + – 1 = 54 (см²)

Відповідь: 54 cм²

Задача 2. Обчислити площу трикутника  зі  сторонами 8,5 см, 12,5 см,  14 см.

Розв’язання:

За формулами планіметрії

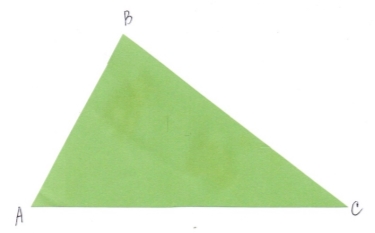
Рис.2.3

АВС – трикутник

АВ = 8,5 см, ВС = 12,5 см, АС = 14 см.

,  ,  = 52,5 (см²)

Відповідь: 52,5 см²

За теоремою Піка

Розмістивши на трикутнику палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину трикутника (В), кількість вузлів решітки, які потрапили на границю трикутника (Г).

Обчислимо площу трикутника за формулою: S = В + – 1.

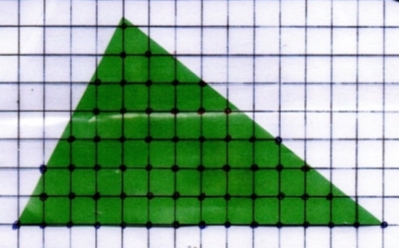
Рис.2.4

В =  45,  Г = 17, S = В + – 1 = 45 + – 1 = 52,5(см²)

Відповідь: 52,5 см²

Задача 3. Обчислити площу трапеції з основами 6 см і 12 см, висотою 8 см.

Розв’язання:

За формулами планіметрії

Рис.2.5

ABCD – трапеція, BC = 6 см, AD = 12 см, ВН = 8 см

= ВН = 8 = 72 (см²)

Відповідь: 72 cм²

За теоремою Піка

Розмістивши на трапецію палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину трапеції (В), кількість вузлів решітки, які потрапили на границю трапеції (Г).

Обчислимо площу трапеції за формулою: S = В + – 1.

Рис.2.6

В = 61, Г = 24, S = В + – 1 = 61 + – 1 = 72(см²)

Відповідь: 72 cм²

Задача 4. Обчислити площу фігуру неправильної геометричної форми.

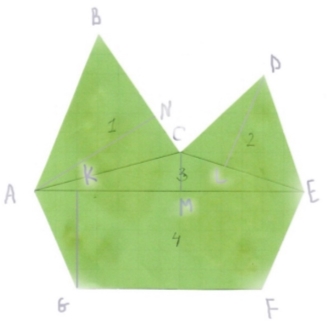
Рис.2.7

Розв’язання:

Для обчислення площі фігури використаємо метод сум.

Далі обчислюємо площу трикутників ∆ABC, ∆DCE,  ∆ACE і  трапеції AEFG.

S_∆АBC =  BC AN = 7 7 = 24,5 (см²)

S_∆DCE =   CE DL = 6 5,5 = 16,5 (см²)

S_∆ACE =   AE CM = 7 6 = 13 (см²)

S_AEFG = GK = 5 = 55 (см²)

  S_ф = S₁ + S₂ + S₃ + S₄  = 24,5+16,5+13+55 = 109 (см²)

Відповідь: 109 cм²

За теоремою Піка

Розмістивши на багатокутник палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину багатокутника (В), кількість вузлів решітки, які потрапили на границю багатокутника (Г).

Обчислимо площу фігури за формулою: S = В + – 1.

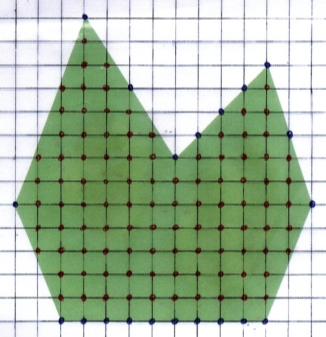
Рис.2.8

В = 100, Г = 20, S = В + – 1 = 100 + – 1 = 109(см²)

Відповідь: 109 cм²

Унаслідок  виконаного дослідження  можемо зробити висновок:

відповіді, отримані при знаходженні площ багатокутників за допомогою формул  планіметрії та теоремою Піка, збігаються. Теорема Піка дає швидке і просте розв’язання задач на знаходження площі фігури.

2.                Обчислення  площі круга та його частин

Обчислимо площі круга та його частин за допомогою формул  планіметрії та за допомогою теореми Піка та порівняємо отримані результати.

Задача 1. Обчислити площу круга радіусом 7 см.

Розв’язання:

За формулами планіметрії

Рис.2.9

R = 7 см, π = , S =  πR² =  154 (см²)

Відповідь: 154 см²

За формулою Піка

Розмістивши на круг палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину круга (В), кількість вузлів решітки, які потрапили на границю круга (Г).

Обчислимо площу круга за формулою: S = В + – 1.

Рис.2.10

В = 148, Г = 22, S = В + – 1 = 148 + – 1 = 158 (см²)

Відповідь: 158 см²  

Задача 2. Обчислити площу сектора радіусом 7 см. Який містить дугу кола

в 135⁰.

Розв’язання:

За формулами планіметрії

Рис.2.11

R = см,  n =135⁰,  π = S_сек = = = (см²)

Відповідь: 57,75см²                                                                                                                                                                                                                      

За формулою Піка  

Розмістивши на сектор палетку з розміром клітини  1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину сектора (В), кількість вузлів решітки, які потрапили на границю сектора (Г).

Обчислимо площу сектора за формулою: S = В + – 1.

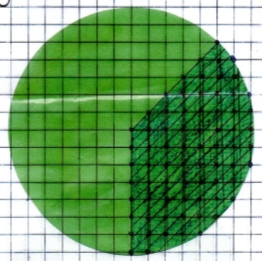
Рис.2.12

В = 53, Г = 19, S = В + – 1 = 51 + – 1 = 59,5 (см²)

Відповідь:   59,5 см²

Задача 3. Обчислити площу кругового кільця, обмеженого двома концентричними колами, радіуси яких дорівнюють 7 см і 2 см.

Розв’язання:

За формулами планіметрії

Рис.2.13

R=7 см, r =2 см, π =

(7² – 2²) = 45 π =141 (см²)

Відповідь: 141 см²

За формулою Піка

Помістити на кругове кільце палетку з розміром клітини 1 см на 1 см,  знайдемо кількість вузлів решітки, які потрапили всередину кругового кільця (В), кількість вузлів решітки, які потрапили на границю кругового кільця (Г).

Обчислити площу кругового кільця за формулою: S = В + – 1.

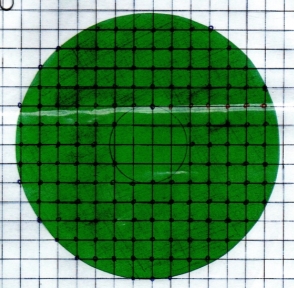
Рис.2.14

В = 132, Г = 16, S = В + – 1 = 132 + – 1 = 139 (см²)

Відповідь: 139 см²

Унаслідок  виконаного дослідження  можемо зробити висновок:

відповіді, отримані при знаходженні площі круга та його частин,  за допомогою формул  планіметрії та теоремою Піка, не збігаються. Використання теореми Піка для знаходження площі круга, кругового сектора або кільця недоцільно, оскільки вона дає наближений результат.

3.                Експеримент і дослідження

Останнім випробуванням будь-якого методу

повинні бути  його практичні результати

Карл Поппер

      Площа – найважливіша характеристика будь-якої земельної ділянки. Необхідність у визначенні площі виникає і під час аналізу дистанційного зондування Землі, вирішення містобудівних завдань, проведення рекреаційних робіт, планування будівельних майданчиків, прогнозування територій підтоплення та лісових пожеж, під час складання кадастрових планів сільськогосподарських угідь, у лісовпорядкуванні, екології, геології. Для цього існують спеціальні методи.

Однак у деяких випадках можна оцінити площу географічного об’єкта,  зображеного на карті, на супутниковому знімку або плані  більш простим способом. Саме для цього і спробуємо використати формулу Піка. Обчислення площі за її допомогою є доволі простим, хоча й має деяку похибку (за результатами дослідження, у середньому 4,5%), отже,  є достатньо ефективним.

         Експеримент був проведений для того, щоб з'ясувати,  чи є знаходження площі географічного об’єкта, зображеного на супутниковому знімку,  дрібномасштабній географічній карті,  та земельної ділянки, зображеної на плані за допомогою формули Піка, ефективним.

Були розглянуті дрібномасштабні географічні карти України, з різним масштабом (1:15 000 000, 1:12 000 000, 1:10 000 000, 1:8 000 000,

1:6 000 000, 1:5 000 000), на них поміщали палетку з розміром клітини  1 см на 1 см,  та знаходили кількість вузлів решітки, які потрапили всередину територій (В), кількість вузлів решітки, які потрапили на границю (Г). За теоремою Піка (S = В + – 1) знаходили значення площі у квадратних сантиметрах, після чого використали  формулу,  що враховує масштаб карти   S = (В + – 1) та перевели отримані значення у квадратні кілометри.  Результати внесені в таблицю (Додаток таблиця 2.1).

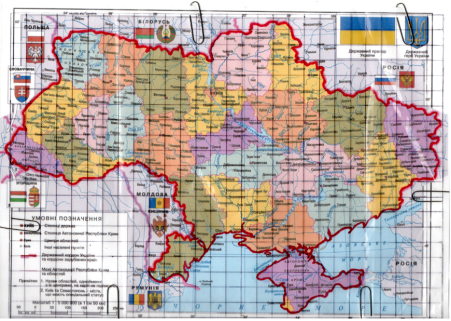
Рис.2.14

  Унаслідок  виконаного дослідження  можемо зробити висновок:

площа території, зображеної на дрібномасштабній географічній карті, знайдена за  теоремою Піка, є наближеною. Точність обчислень залежить від величини масштабу: чим менший масштаб, тим більша похибка; чим більший масштаб, тим менша похибка. Середня похибка обчислень становить 5%.

                 Для порівняння були розглянуті різні географічні об’єкти зображені на дрібномасштабній географічній карті з одним масштабом: Чернігівська область та її райони (1:1 300 000) . Результати внесені в таблицю. (Додаток таблиця 2.2).

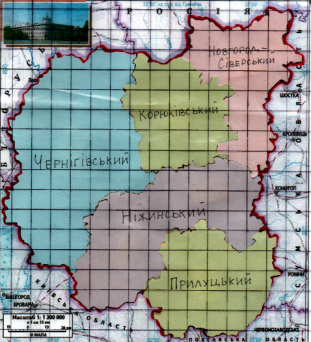
Рис.2.16

           Унаслідок  виконаного дослідження  можемо зробити висновок:

площа території, зображеної на дрібномасштабній географічній карті, знайдена за  теоремою Піка, є наближеною. Точність обчислень залежить від кривизни границі об'єкта. Середня похибка обчислень становить 7,8 %.

              Також були розглянуті  плани земельних ділянок  з масштабом 1:100, 1:250 та 1:500 та обчислені їх площі.  Результати внесені в таблицю. (Додаток таблиця 2.3).

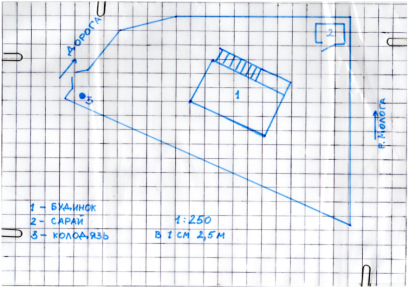
Рис.2.17

           Унаслідок  виконаного дослідження  можемо зробити висновок:

площа земельної ділянки, зображеної на плані,  знайдена за  теоремою Піка, співпадає з кадастровими даними. Пропонуємо застосувати теорему Піка для спрощення обчислень площі земельної ділянки,  зображеної на плані.

           Однім із аспектів використання Дистанційне зондування Землі є обчислення площ географічних об’єктів. Впродовж останнього часу космічні знімки стали значно доступнішими для споживачів такої продукції та можуть застосовуватися для досліджень. Нами були розглянуті супутникові данні географічних об’єктів: Міжрічинський регіональний ландшафтний парк, м. Чернігів,  м. Одеса. Результати внесені в таблицю. (Додаток таблиця 2.4).

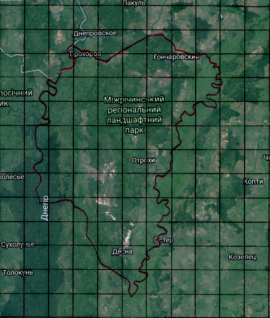
Рис.2.18

           Унаслідок  виконаного дослідження  можемо зробити висновок:

площа території, зображеної на супутникових знімках, знайдена за  теоремою Піка, є наближеною. Точність обчислень залежить від кривизни границі об'єкта. Середня похибка обчислень становить 5 %.

ВИСНОВКИ

Для перевірки теореми Піка ми виконали експериментальні дослідження, а саме  визначали площу фігури за допомогою формул планіметрії та теореми Піка. Ми перевірили справедливість теореми Піка для багатокутників і кола та його частин. Порівнявши отримані результати, ми впевнилися, що теорема Піка надає точні відповіді для багатокутників та наближені – для кола та його частин.

Другим етапом нашого дослідження було вимірювання площі різних географічних об’єктів,  зображених на  дрібномасштабній географічній карті, земельних ділянок, зображених на плані та географічні об’єкти на супутникових знімках. Проаналізувавши отримані результати, дійшли такого висновку: знайти площу географічного об’єкта, зображеного на дрібномасштабній географічній карті та супутниковому знімку за теоремою Піка набагато простіше, але отримані значення будуть наближені до дійсних. Точність обчислень залежить від величини масштабу і кривизни границі об'єкта. А при визначенні  площі земельних ділянок, що мають вигляд багатокутників, зображених на плані, отримали точне значення.

        Виконані дослідження дають підстави рекомендувати теорему Піка для визначення площ географічних об’єктів,  зображених на дрібномасштабній географічній карті, земельних ділянок, зображених на плані, та географічних об’єктів на супутникових знімках. Завдання, поставлені на початку роботи, виконані. Гіпотеза –  площу географічного об’єкта, зображеного на дрібномасштабній географічній карті,  земельної ділянки, зображеної на плані, та географічного об’єкта зображеного на супутникових знімках можна обчислити за допомогою теореми Піка більш просто та швидко, отримуючи достовірні значення – підтвердилася частково. Формула Піка має значну пізнавальну і практичну цінність.

Виведена формула  S = (В + – 1) для отримання відповіді у квадратних кілометрах виявилась дуже зручною.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Вавилов В. В., Многокутники на сітках/ МЦНМО, 2006 – 72с.;
2. Васильєв Н.В., Навколо формули Піка / Квант, 1974, № 12 с.39 – 43;
3. Віноградов І.М. Математична енциклопедія, у 5 т., М-1985, т. 3, с. 750; т. 4, с. 327;
4. Горіна Л.В., Одна за всіх ... Формула Піка / Математика в школах України: наук. - метод. журн., 2013, № 4 с. 26-30;
5. Жарковський М.Н., Рісс М.А., Геометрія на папері у клітинку/ Математика, 2009, № 172;
6. Кушніренко А., Цілі точки в многоугольниках і многогранниках/ Квант, 1977, № 4 с.13 – 20;
7. Третьяк А. М., «Землеустрій», Олді-плюс,  2018, с520;
8. Шмиг Р.А., Боярчук В.М., Добрянський І.М., Барабаш В.М., Термінологічний словник-довідник з будівництва та архітектури/ за заг. ред. Р. А. Шмига. — Львів, 2010.  с. 143. 
9. Штейнгауз Гуго, «Математический калейдоскоп» М.,Наука, 1981-160 с;
10. Атлас «Україна у світі: природа, населення», 8 клас, Картографія, 2016;
11. Атлас «Чернігівська область», «Мапа», «Моя мала батьківщина», 2003;
12. Вікіпедія. Вимірювання-             
13. Вікіпедія. Пік Георг -             
14. Вікіпедія. Площа фігури-     
15. Вікіпедія. Теорема Піка -
16. Вікіпедія. Дистанційне зондування Землі -
17. Використання даних дистанційного зондування Землі в сучасному освітньому процесі. [https://youtu.be/t8v9Ob6AYDI]

ДОДАТКИ

Таблиця 2.1

Таблиця 2.2

Таблиця 2.3

Таблиця 2.4