Урок "Вектори в просторі. Дії над векторами"

ДПТНЗ «ВІННИЦЬКЕ МІЖРЕГІОНАЛЬНЕ ВИЩЕ ПРОФЕСІЙНЕ УЧИЛИЩЕ  

«Вектори в просторі.  Дії над векторами»

Викладач математики  Капітанчук В.О.

Тема уроку. Вектори в просторі. Дії над векторами

Мета:  

•      Навчальна: сформувати поняття вектора в просторі, рівність та колінеарність векторів, правила додавання, віднімання та множення на скаляр векторів заданих графічно, сформувати вміння розв'язувати задачі, що передбачають використання цих понять;

•      Розвиваюча: розвивати просторову уяву; логічне мислення, творче мислення, розвивати вміння аналізувати умови задач та застосовувати теоретичний матервал до їх розвязання;

•      Виховна: виховувати інтерес до вивчення точних наук; наполегливість; культуру математичного мовлення, самооцінку, розширити кругозір учнів, підвищувати їх інтелектуальний рівень, інтерес до геометрії.

Формування компетентностей:

•      математична компетентність — оперувати числовою інформацією, геометричними об'єктами на площині та в просторі;

•      спілкування державною мовою — доречно та коректно вживати в мовленні математичну термінологію;

•      уміння вчитися впродовж життя — визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; Тип уроку: засвоєння нових знань і вмінь.

Очікувані результати навчально-пізнавальної діяльності учнів:

üнаводить приклади моделей векторів та векторних величин об’єктів навколишнього середовища; 

üформулює означення, ознаки, властивості понять, зазначених у змісті навчального матеріалу; 

üрозрізняє векторні і скалярні величини; рівні вектори, колінеарні вектори; ü класифікує взаємне розміщення двох (трьох) векторів у просторі; 

ü зображає на рисунку правила додавання векторів (трикутника та паралелограма); суму/різницю векторів, добуток вектора на число; 

üзнаходить на рисунку та зображає напрямлений відрізок як вектор, що дорівнює  сумі, різниці векторів, добутку вектора на число; 

üобґрунтовує перпендикулярність, колінеарність та компланарність векторів простору; скалярний добуток векторів;

üілюструє текстовий зміст геометричних тверджень та задач за допомогою рисунка;

ü характеризує координатний і векторний методи розв'язування задач;  

 

Хід уроку

I.                Організаційний етап

•      Привітання

•      Перевірка присутніх на уроці

•      Налаштування на роботу

II.            Мотивація навчальної діяльності.

Проблемне питання

Перегляньте відео і дайте відповідь на запитання. Що об'єднує фізиків, авіадиспетчерів і розробників відеоігор?

 

 

Діяльність учнів:

Учні переглядають відео і дають відповіді на запитання.

Діяльність викладача:

Викладач підводить підсумки, за результатами відповідей учнів.

Поняття вектора є важливим у математиці та фізиці. Існує чимало важливих величин, котрі є векторами. Наприклад, сила, швидкість, прискорення, кутовий момент, напруженість електричного і магнітного полів. Ці величини можна протиставити іншим величинам, таким як маса, об’єм, тиск, температура та густина, які можна описати звичайним числом, їх називають скалярами. Тому знання про вектори є важливими при вивченні природничо-математичних наук. Сьогодні на уроці ми повторимо  знання  про вектори в просторі, розглянемо задачі , що передбачають використання  властивостей додавання та віднімання векторів (графічно). Оскільки тему «Вектори» ви вже вивчали в курсі геометрії 9-го класу. Спробуємо пригадати відомі нам факти і провести паралель між теорією  вектор на площині і вектор в просторі.

III.     Пояснення нового матеріалу

1. Означення вектора. 

У вигляді фронтальної бесіди обговорити питання:

•      Що таке вектор?

•      Як позначається вектор?

•      Що таке нуль вектор?

•      Що таке довжина вектора (модуль вектора) ?

 

Діяльність учнів:

Учні дають відповіді на запитання:

•      Чи існує вектор який немає довжини?

•      Чи існує вектор який немає напрямку ?

•      Чи можна вважати будь-яку точку площини вектором?

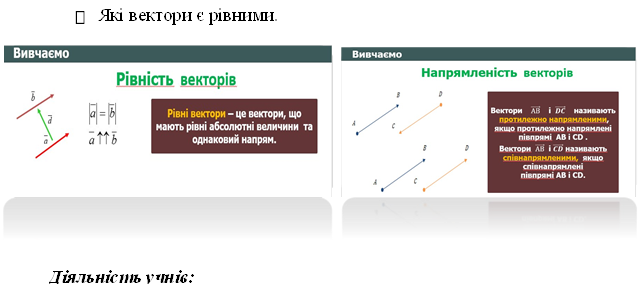
2. Напрямленість векторів. Рівність векторів.

У вигляді фронтальної бесіди обговорити питання:

 Які вектори є співнапрямленими, протилежно напрямленими, як вони зображаються.

Учні дають відповіді на запитання:

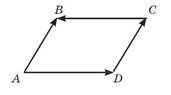
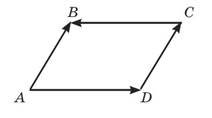№1 На рисунку зображено паралелограм ABCD.

а) Які вектори є співнапрямленими?

б) Які вектори є протилежно напрямлені? 

в) Які вектори рівні?

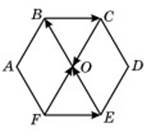№12.5  ABCDEF –правильний шестикутник. Запишіть усі пари:

а) Рівних векторів; 

б) Рівних за модулем, але протилежно напрямлених, векторів.

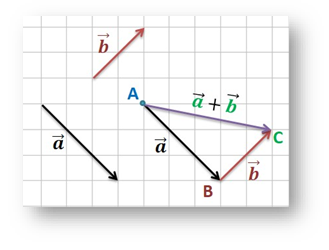
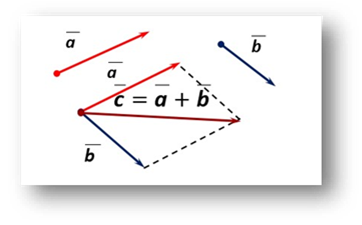
3.     Сума  векторів.

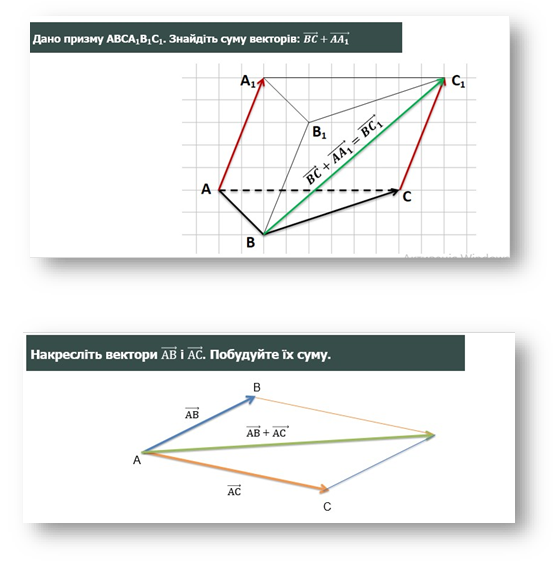
Обговорюємо правила суми векторів: правило трикутника та паралелограма.

Щоб знайти суму векторів  за правилом трикутника треба:
	1)  від кінця вектора  відкласти вектор, що дорівнює вектору ; 2)  побудувати вектор, початок якого збігається  з початком вектора , а кінець – з кінцем вектора , він і є сумою векторів .

Щоб знайти суму векторів  за правилом паралелограма треба: 1)    вектори перенести паралельно самим собі так, щоб їх початки збігалися; 2)    Вектор суми задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку.

 

Діяльність учнів:

Учні розв’язують вправи з колективним обговоренням:

 

 

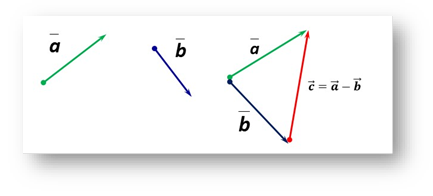
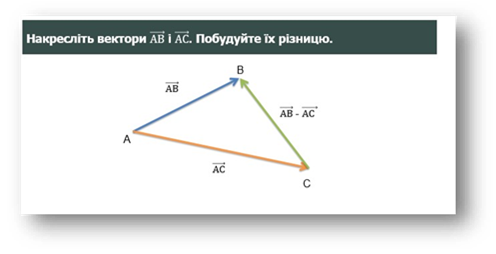
4.     Різниця векторів.

Щоб знайти різницю векторів  треба: 1)    відкласти вектори        від однієї точки; 2)    побудувати вектор, початок якого збігається з кінцем вектора , а          кінець з кінцем вектора , він і буд е різницею векторів

Діяльність учнів:

Учні розв’язують вправи з колективним обговоренням 

 

5.     Колінеарність векторів.

Вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

 

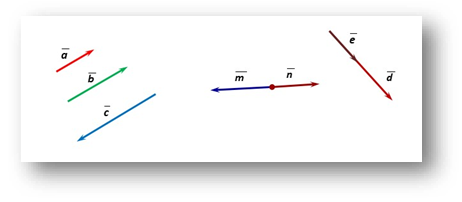
Діяльність учнів:

Учні розв’язують вправи з колективним обговоренням 

1.     Назвіть пари колінеарних векторів.

 

2.     Назвіть три пари колінеарних векторів.

 

6. Добуток вектора на число.

Добутком ненульового вектора ⃗𝒂⃗  і числа k, відмінного від нуля, називають такий вектора 𝒃⃗ , що: 1)  | 𝐛| = |𝐤||𝐚⃗ |; 2)  Якщо 𝐤 < 𝟎, то 𝐛 ↑↑ 𝐚⃗ ; якщо 𝐤 > 𝟎, то 𝐛 ↑↓ 𝐚⃗ .

 

 

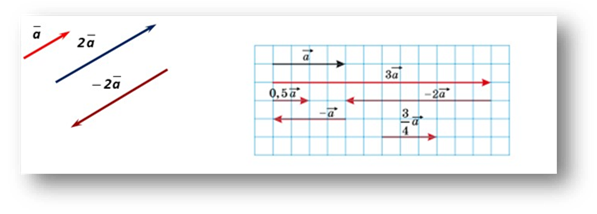
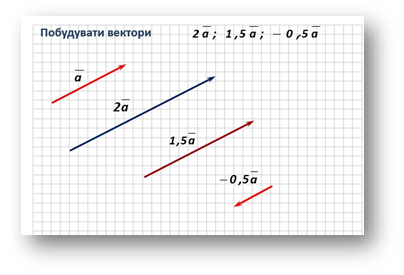
IV.             Закріплення вивченого матеріалу.

Мета етапу:

Забезпечити засвоєння навчального матеріалу, досягнення результатів уроку.

Учні проходять тестування https://www.classtime.com/student/login/VJQQ44

Діяльність викладача:

 Вчитель підбиває коментує результати тестування і ще раз звертає увагу на найбільш проблемні запитання. 

 

V.                Рефлексія.

Мета етапу:

•      Вираження почуттів, що виникли в учнів у ході уроку.

Діяльність викладача:

Давайте з вами разом проголосуємо та визначимо наскільки плідно і творчо ми з вами попрацювали.

Діяльність учнів:

Із допомогою програми Mentimeter, учні дають відповіді на запитання та переглядають результати на екрані.

VI.             Домашнє завдання.

Мета етапу:

•      Розвивати самостійність та творче мислення • Удосконалювати методи самостійної роботи

Опрацювати§12 Виконати № 12.6; 12.8; 12.10; 12.14