Тема. Розв’язування найпростіших тригонометричних нерівностей.

Мета:

• формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: sin x > a, sin x < a, cos x < a, cos x > a, (sin x  a, sin x  a,         cos x   a, cos x  a);
• розвивати навички мислення учнів, їх пізнавальні інтереси;
• виховувати організованість та дисципліну розумової праці учнів.

Тип уроку: урок засвоєння нових знань.

Обладнання: підручник  алгебра 10 клас, таблиця із розв’язками тригонометричних нерівностей, комп’ютери, циркуль, лінійка.

Хід уроку

І. Організація класу.

ІІ. Перевірка домашнього завдання.

1. Які є питання щодо виконання  домашнього завдання?
2. Всі виконали домашнє завдання?
3. Перевірка домашнього завдання.

ІІІ. Підведення підсумків попередніх знань

В цьому розділі тригонометрії ми навчилися знаходити значення обернених функцій, розв’язувати найпростіші тригонометричні рівняння, системи тригонометричних рівнянь. Для того щоб сьогодні здобути нові знання, мені потрібно знати, як ви опанували попередній матеріал кожний. Тому зараз ми проведемо тести із 9 учнями на комп’ютерах , а 5 сильніших розв’яжуть тригонометричні рівняння.

1.Учні сідають за комп’ютери і розв’язують 20 питань у вигляді тестів по темі “Обернені функції”

2.Сильніші учні розв’язують на картках системи тригонометричних рівнянь

          1)     2) 

 

3)   4)

5)

ІV. Актуалізація опорних знань.

 Давайте ще раз пригадаємо:

1. Як виглядає розв’язок рівняння sin x = a
2. Як виглядає розв’язок рівняння cos x = a
3. Як виглядає розв’язок рівняння tg x = a

V. Мотивація навчальної діяльності учнів

При дослідженні реальних процесів, що описуються за допомогою тригонометричних функцій, часто виникає потреба в знаходження знань аргументу, при яких функціях набуває значень, більших або менших за деяке число. Це завдання зводиться до розв’язування найпростіших тригонометричних нерівностей.

 Як їх розв’язувати? Як записувати розв’язки? – питання на які ми будемо давати відповідь під час уроку.

VІІ. Повідомлення теми та мети уроку.

VІІІ. Пояснення нового матеріалу

Як ви думаєте, яка нерівність називають тригонометричною?

 (Якщо вона містить змінну тільки під знаком тригонометричної функції)

Наприклад: sin 3x > 1, cos x + tg x < 1

 Весь демонстраційний матеріал показую  у вигляді презентації

Розв’язати тригонометричну нерівність означає знайти множину значень змінної, при яких нерівність виконується.

Розв’язання тригонометричних нерівностей зводиться до розв’язування нерівностей: sin x > a, sin x < a, sin x  a, sin x  a, cos x > a, cos x < a,
cos x  a, cos x  a, tg x >a, tg x < a, tg x  a, tg x  a. Ці нерівності називаються найпростішими.

Отже, мета сьогоднішнього уроку - навчитися розв’язувати найпростіші тригонометричні нерівності.

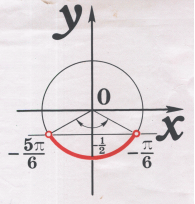1)Розглянемо нерівність

Позначимо функції, які стоять у  лівій і правій частині, через у =sin x i  y = - ½. Побудуємо схематично графіки  цих функцій. Розв’язком будуть абсциси  всіх точок графіка синусоїди. Які  розміщені нижче від прямої у =-½. Оскільки синус періодична функція,  досить знайти розв’язки на будь-якому  відрізку області визначення завдовжки 2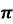 і додати до знайдених чисел період 2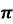n, n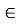Z. Виберемо, наприклад, проміжок [0;2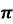]. З малюнка видно, що множиною значень х з відрізка [0;2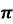], для яких відповідні точки графіка синусоїди розміщені нижще від точок прямої у = - ½ , буде [-¾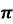; -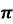/4]

  Враховуючи періодичність маємо

[-¾+2n; -/4 + 2n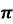], n є Z.

2)На дошці учень пробує знайти розв’язок нерівності

( учні дивляться на таблицю, де нерівності розв’язані графічним способом)

Отже ми можемо зробити висновок, що графічний спосіб є досить наочним, але незручність полягає в тому, що кожного разу (хоч і схематично) треба будувати графіки тригонометричних функцій.

Дещо зручнішим є спосіб розв’язування простіших тригонометричних нерівностей за допомогою одиничного кола.

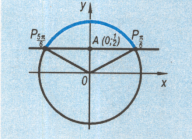
Будуємо одиничне коло. Відкладаємо на осі Оy ординату  ½  і через точку проводимо пряму паралельну осі Оx.

Розв’язування даної нерівності зводиться до знаходження на одиничному колі всіх точок, у яких ординати більші . Ці точки є розв’язками тригонометричних нерівностей.

Нагадаємо: вісь синусів співпадає з віссю Оy, Оx - косинусів.

IX. Закріплення вивченого матеріалу.

1.Розв’язати нерівність cos x < 2/2 (колективно)

 

    

 

 

 

2.Розв’язати нерівність cos x   3/2 (самостійно)

X. Узагальнення отриманих знань.

У загальному випадку розв’язком нерівністі sin x > a, де -1  а 1 є множина (arcsin a; - arcsin a), а множиною всіх розвязків будуть проміжки:

                                       arcsin a+ 2n <x< 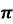- arcsin a +2n

Розв’язками нерівності виду sin x > a, cos x >a є множина всіх дійсних чисел, якщо  а  -1, якщо  а1, то дані нерівності розв’язків не мають.

Розв’язками нерівності виду sin x < a, cos x < a є множина всіх дійсних чисел, якщо  а 1, якщо а<-1 то дані нерівності розв’язків не мають

Наприклад

sin x>-1,2. Відповідь: xЄR

sin x>1,2. Відповідь: нерівність розв’зків не має.

cos x<7,5. Відповідь: xЄR

cos x>-3. Відповідь: нерівність розв’зків не має.

 

XI. Підсумок уроку.

Треба пам’ятати:

1) записуючи проміжок слідкують, щоб зліва  було менше число, а справа – більше, що відповідає на колі руху проти годинникової стрілки;
2) відповіді записують з урахуванням періоду

XII.Домашнє завдання.

§15. Вправа 61.(1-3)