Теоретичний матеріал. Функції.
ФУНКЦІЇ
|
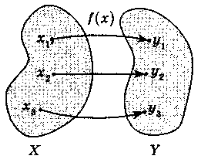
Функція — це залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у. |
|||||
|
|
Позначається: y = f(x), де х — аргумент (незалежна змінна); у — функція, значення функції (залежна змінна);f(x0) — значення функції в точці х0. |
||||
|
Приклад. Дано функцію f(x) = x2-3х + 2. Знайдемо: 1) f(0)2) f(-1);3) f(а). Розв’язання |
|||||
|
1)f (0) = 02–3 ∙ 0 + 2 = 2; 2)f (-1) = (-1)2–3 ∙ (-1)+2 = 6; 3)f(a) = a2– 3a + 2. |
|||||
|
|
Область визначення функції D(f)— це множина всіх значень, яких набуває аргумент. |
|
|||
|
|
Як знайти область визначення функціїy = f(x) |
|
|||
|
|
1.Якщо f(x) — многочлен, то D(f) = R. |
|
|||
|
2.Якщо |
|||||
|
3.Якщо |
|||||
|
Приклад.Знайдемо область визначення функції: |
|||||
|
|
Розв'язання |
|
|||
|
|
1) 3х2–х+ 1— многочлен, тому D(y) = R;
2)
3)
Отже, D(y)= (-∞; 0) |
|
|||
|
|
Область значень функції E(f)— множина всіх значень змінної у, яких вона може набувати при всіх значеннях аргументу, взятих з D(f). |
|
|||
|
|
Приклад. Знайдемо область значень функції у = Розв'язання |
|
|||
|
|
При всіх x |
|
|||
|
|
Числовою функцієюназивають функцію, область визначення й область значень якої є числовими множинами. |
|
|||
|
|
Графіком функціїy = f(x)називають множину всіх точок координатної площини з координатами (х; f(x)), де х «пробігає» всю область визначення f(x) (ay — відповідне значення функції / у точці х). |
|
|||
|
|
Деякі елементарні функції та їхні графіки |
|
|||
|
|
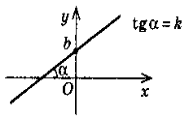
1. y = kx + b—лінійна функція
|
2. у = x2
|
|
||
|
|
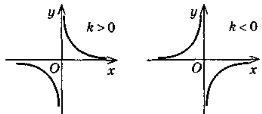
3.у =
|
4.y =
|
|
||
|
|
|
|
|
||
|
|
Найпростіші перетворення графіків функцій |
|
|||
|
|
№ з/п |
Формула залежності |
Приклад |
Перетворення |
|
|
|
1 |
y = -f(х) |
|
Симетрія відносно осі Ох |
|
|
|
2 |
y = f(х)+ a |
|
Паралельне перенесення вздовж осі Оу на а одиниць (якщо а> 0, то вгору, якщо а< 0, то вниз) |
|
|
|
3 |
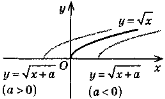
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на +а одиниць (якщо а> 0— вліво, якщо а< 0 — вправо) |
|
|
|
4 |
y = kf(х)(k >0) |
|
Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k> 1, і стиснуто, якщо 0<k<1 |
|
|
|
|
|
|
|
|
|
Функція виду у = ax2+ bx + c, де а |
|||
|
Наприклад: |
|||
|
Графік квадратичної функції — парабола, вітки якої напрямлені вгору, якщо а > 0, і вниз — якщо а < 0 . |
|||
|
Координати вершини (х0;у0)параболи графіка у = ах2 + bх + с обчислюються за формулами: |
|||
|
|
|||
|
Наприклад: у функціїу = х2+2х–3, яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини: |
|||
|
|
|||
|
або y0 = f (-1) = (-1)2+2 ∙ (-1)–3= 1–2–3= -5 + 1 = -4. |
|||
|
Тобто вершина параболи (-1; - 4). |
|||
|
|
Побудова графіка функції у = ах2 + bх + с, а |
|
|
|
|
Спосіб1 |
Спосіб2 |
|
|
|
1.Обчислити абсцису вершини |
1.Виділити повний квадрат:
ах2 +bх + с = а |
|
|
|
2.Підставити х0у рівнянняі знайти у0. 3. Побудувати параболу у = ах2з вершиною в точці (х0;у0).Якщо а >0, вітки параболи напрямлені вгору, якщоа <0— вниз. 4. Для більшої точності побудови знайти точки перетинуграфіка з координатнимиосями. |
= а 2.Використавши схему геометричних перетворень графіківфункцій, виконати побудовупараболи у= х2, потім її розтягнення (або стиснення) до параболи у= ах2, а потім виконатипаралельне перенесення у= ах2вздовж осі Ох на –ті вздовжосі Оуна п. |
|


про публікацію авторської розробки
Додати розробку


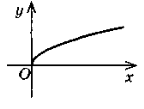


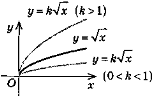
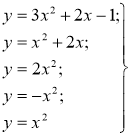 — квадратичні функції.
— квадратичні функції.
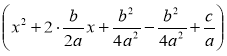 =
=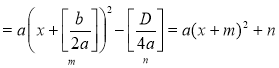 .
.