"Теорія катастроф" (індивідуальне науково-дослідницьке завдання)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

           Чернівецький національний університет імені Юрія Федьковича

Теорія катастроф

(індивідуальне науково-дослідницьке завдання)

                                                                                                  Виконала:

                                                                                               студентка 2-го курсу

                                                                                                     201 групи

                                                                                                     Чугаєвська І.І.

                                                                                                     Викладач:

 Романів Л. В.

Чернівці

2012

Зміст роботи

Вступ………………………………………………………………………...3

1. Історія……………………………………………………………………4
2. Сім елементарних катастроф по Тому…………………...……………4

            2.1 Потенційні функції з однієї активної змінної……………………5

                       2.1.1 Катастрофа типу "Складка"……………………………...5

                            2.1.2 Катастрофа типу "Збірка"………………………………..6

   2.1.3 Катастрофа типу "ластівчин хвіст"……………………..8

   2.1.4 Катастрофа типу "Метелик"…………………………….9

  2.2 Потенційні функції з двома активними змінними………….….10

   2.2.1 Гіперболічна омбіліка…………………………………..10

   2.2.2 Еліптична омбіліка……………………………………..10

   2.2.3 Параболічна омбіліка…………………………………..10

3. Запис і класифікація катастроф по Арнольду……………………………10

4. Застосування теорії катастроф……………………………………………11

5. Список використаної літератури………………………………………....12

Вступ

Теорія катастроф - розділ математики, що включає в себе теорію біфуркацій диференціальних рівнянь ( динамічних систем) і теорію особливостей гладких відображень.

Терміни "катастрофа" і "теорія катастроф" були введені Рене Томом (Ren Thom) і Крістофером Зіманов (Christopher Zeeman) наприкінці 1960-х - початку 1970-х років ("катастрофа" в даному контексті означає різке якісна зміна об'єкту при плавному кількісному зміну параметрів, від яких він залежить). Однією з головних задач теорії катастроф є отримання так званої нормальної форми досліджуваного об'єкта (диференціального рівняння або відображення) в околиці "точки катастрофи" і побудована на цій основі класифікація об'єктів.

Теорія катастроф знайшла численні застосування в різних областях прикладної математики, фізики, а також в економіці.

1. Історія

Перші фундаментальні результати в області динамічних систем, пов'язані з теорії катастроф, належать А. Пуанкаре (метод нормальних форм в теорії диференціальних рівнянь) і А. А. Андронову (біфуркації динамічних систем). Основи теорії особливостей гладких відображень були закладені насамперед у працях американського тополог Хасслера Уїтні (Hassler Whitney) в 1940-х - 1950-х рр.., яким передувала лема Морса про нормальну формі функції в околиці невиродженої критичної точки.

В кінці 1960 -х розвитком цього напряму зайнявся відомий французький математик і Філдсівську лауреат 1958 року Рене Том. Проте популярність ідеї Уїтні і Тома придбали завдяки декільком публікаціям К. Зімана в 1970 -х, який активно пропагував теорію катастроф, порівнюючи її значення з винаходом математичного аналізу і кажучи про "революцію в математиці". Бурхливий розвиток теорії катастроф в 1970-і - 1990-і роки пов'язано з діяльністю Дж. Боардмана, Є. Бріскорна, Дж. Брюса, Дж. Мазера, Б. Мальгранжа, Р. Тома, Т. Волл, К. Зімана і особливо В. І. Арнольда і його учнів (А. ​​Н. Варченко, В. А. Васильєв, А. Б. Гівенталь, В. В. Горюнов, С. М. Гусейн-Заде, А. А. Давидов, В. М . Закалюкін, В. Д. Сєдих та ін.)

2. Сім елементарних катастроф по Тому

Теорія катастроф аналізує критичні точки (репетиції) потенційної функції, тобто точки, де не тільки перша похідна функції дорівнює нулю, а й дорівнюють нулю ж похідні вищого порядку. Динаміка розвитку таких точок може бути вивчена за допомогою розкладання потенційної функції в рядах Тейлора допомогою малих змін вхідних параметрів. Якщо точки росту складаються не просто в випадковий шаблон, але формують структуровану область стабільності, ці точки існують як організуючі центри для особливих геометричних структур з низьким рівнем катастрофічності, з високим рівнем катастрофічності в оточуючих їх областях фазового простору. Якщо потенційна функція залежить від трьох або меншої кількості активних змінних, і п'яти-менш активних параметрів, то в цьому випадку існує всього сім узагальнених структур описаних геометрій біфуркацій, яким можна приписати стандартні форми розкладань в ряди Тейлора, в які можна розкласти репетиції за допомогою діффеоморфізма (гладкою трансформації, обіг якої також гладко). Сьогодні ці сім фундаментальних типів катастроф відомі під іменами, які їм дав Рене Том.

2.1. Потенційні функції з однієї активної змінної

2.1.1. Катастрофа типу "Складка"

Стабільна і нестабільна частини екстремуму, який зникає при біфуркації типу "складка"

V = x ³ + a x

Стабільна і нестабільна частини екстремуму, який зникає при біфуркації типу "складка"

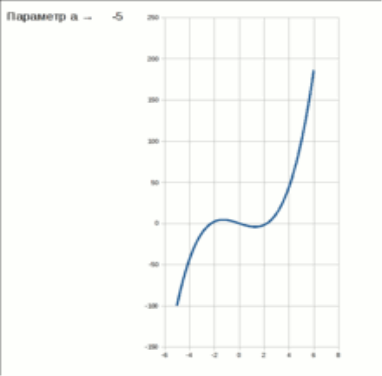
При негативних значеннях параметра a, потенційна функція має два екстремуми - один стабільний (стійка рівновага) і один нестабільний (нестійка рівновага). Якщо параметр a повільно змінюється, система може перебувати в точці стабільного мінімуму. Але якщо a = 0, стабільні і нестабільний екстремуми зустрічаються і анігілюють. Це - точка біфуркації. При a> 0 не існує стабільного рішення.

Якщо фізична система проходить через точку біфуркації типу "згортка", і тому параметр a досягає значення 0, стабільність рішення при a <0 раптово втрачається, і система може здійснити раптовий перехід у нову, дуже відмінне від попереднього стан. Це біфуркаційні значення параметра a іноді називається "точкою фіксації".

2.1.2.   Катастрофа типу "Збірка"

V = x ⁴ + a x ² + b x

Діаграма катастрофи "збірка" з точкою повернення, на якій показані криві (коричневі, червоні) по змінній x, що задовольняють висловом для параметрів (a, b), криві показані для безперервно змінюється параметра b при різних значеннях параметра a. Поза геометричного місця точок повернення (синя область) для кожної точки (a, b) у фазовому просторі існує тільки одне екстремальне значення змінної x. Усередині точок повернення існує два різних значення x, які дають локальні мінімуми функції V (x) для кожної пари (a, b). При цьому вказані значення розділені локальним максимумом.

Біфуркація типу "вилка" при a = 0 на просторі b = 0. Форма точок повернення в фазовому просторі (a, b), близько точки катастрофи, показує геометричне місце біфуркацій типу "згортка", яке розділяє область з двома стабільними рішеннями і область з одним рішенням. Геометрія точок повернення досить звичайна, коли проводиться вивчення того, що відбувається з біфуркації типу "згортка" при додаванні в управляє простір нового параметра b. Змінюючи параметри, можна знайти, що є крива (синя) точок у просторі (a, b), на якій втрачається стабільність, тобто на цій кривій стабільне рішення може раптово "перестрибнути" на альтернативне значення (також стабільне).

Але в геометрії точок повернення крива біфуркацій загортає назад, створюючи друга гілка, на якій вже це друге рішення втрачає стабільність, а тому може зробити "стрибок" назад на початкове безліч рішень. При повторному збільшенні значення параметра b і наступному зменшенні його, можна спостерігати гістерезис в поведінці петель, оскільки система слід по одному рішенню, "перестрибує" на інше, слід по ньому і "перестрибує" назад на вихідне.

Однак це можливо тільки в області у параметричному просторі при a <0. Якщо значення параметра a збільшується, петлі гістерезису стають менше і менше, поки значення a не досягне 0. У цій точці петлі зникають (катастрофа з точкою повернення), і з'являється лише одне стабільне рішення.

Також можна розглянути процес зміни параметра a при незмінному значенні b. У симетричному випадку при b = 0 можна спостерігати біфуркацію типу "вила" при зменшуваному значенні параметра a одне стабільне рішення раптово поділяється на два стабільних рішення і одне нестабільне. У цей час фізична система проходить в область a <0 через точку повернення (a = 0, b = 0) (це - приклад спонтанного порушення симетрії). Далеко від точки повернення не існує раптових змін у фізичній системі, оскільки при проходженні по кривій біфуркації згортки відбувається тільки те, що стає доступним Другий альтернативний рішення.

Одне з найбільш цікавих пропозицій для Вашого катастрофи з точкою повернення полягає в тому, що цей тип катастрофи можна використовувати для моделювання поведінки собаки, яка у відповідь на зовнішній вплив може злякатися або розлютило. Пропозиція полягає в тому, що при помірному впливі (a> 0) собака буде проявляти плавну зміну відгуку з переляку на злість в залежності від того, як було проведено вплив. Але більш високий рівень впливу - це стрес, відповідний переходу в область a <0. В цьому випадку якщо собака спочатку злякалася, вона залишиться переляканою при збільшенні рівня впливу на неї, поки в кінцевому підсумку вона не досягне точки повернення, де відбудеться спонтанний перехід в режим злоби. При переході в цей режим собака буде залишатися озлобленої навіть у разі поступового зниження впливу на неї.

Інший приклад прикладного застосування катастрофи з точкою повернення полягає в моделюванні поведінки електрона при переміщенні з одного енергетичного рівня на інший, що часто спостерігається в хімічних і біологічних системах. Це вказує на те, що біфуркації розглянутого типу та геометрія точок повернення є найбільш важливою практичною частиною теорії катастроф. Це - шаблони, які проявляються знову і знову у фізиці, інженерії та математичному моделюванні.

Решта прості геометрії катастроф є більш спеціалізованими в порівнянні з тільки що розглянутим, а тому виявляються тільки в деяких окремих випадках.

2.1.3. Катастрофа типу "ластівчин хвіст"

V = x ⁵ + a x ³ + b x ² + c x

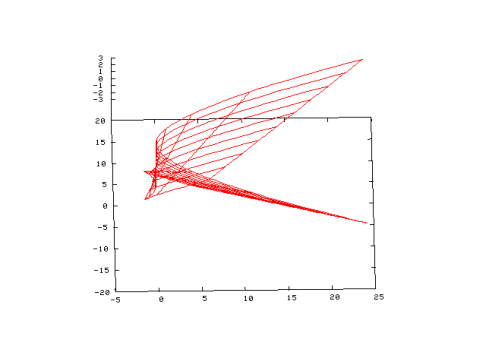
Керуючий простір у даному типу катастроф є тривимірним. Каскад біфуркацій у фазовому просторі складається з трьох поверхонь біфуркацій типу "згортки", які зустрічаються на двох кривих біфуркацій з точками повернення, які в кінцевому підсумку зустрічаються в одній точці, що представляє собою біфуркацію типу "ластівчин хвіст".

У міру проходження значень параметрів по поверхнях областей біфуркацій типу "згортка" пропадає один мінімум і один максимум потенційної функції. В області біфуркацій з точкою повернення два мінімуми і один максимум заміщуються одним мінімумом; за ними біфуркації типу "згортка" зникають. У точці ласточкиного хвоста два мінімуми і два максимуми зустрічаються в одному значенні змінної x. Для значень a> 0 за ласточкиним хвостом існує або одна пара (мінімум, максимум), або не існує взагалі ніяких біфуркацій. Це залежить від значень параметрів b і c. Дві поверхні біфуркацій типу "згортка" і дві лінії біфуркацій з точками повернення зустрічаються при a <0, а тому зникають в самій точці ласточкиного хвоста, замінюючись однією поверхнею біфуркацій типу "згортка". Остання картина Сальвадора Далі під назвою "Ластівчинин хвіст" створена під впливом цього типу катастроф.

2.1.4. Катастрофа типу "Метелик"

V = x ⁶ + a x ⁴ + b x ³ + c x ² + d x

Залежно від значень параметрів потенційна функція може мати три, два чи один локальний мінімум, причому всі мінімуми розділені областями з біфуркації типу "згортка". У точці з поетичною назвою "метелик" зустрічаються три різні простору (тривимірних площині) таких біфуркацій типу "згортка", дві поверхні біфуркацій з точками повернення і скривив біфуркацій типу "ластівчин хвіст". Всі ці біфуркації пропадають в одній точці і перетворюються на просту структуру з точкою повернення тоді, коли значення параметра a стає позитивним.

2.2. Потенційні функції з двома активними змінними

Омбіліческіе катастрофи є прикладами катастроф другого порядку. Вони, наприклад, можуть спостерігатися в оптиці при відображенні світла від тривимірних поверхонь. Самі по собі такі катастрофи тісно пов'язані з геометрією майже сферичних поверхонь. Рене Том запропонував розглядати гіперболічну омбіліческую катастрофу як руйнування хвилі, а еліптичну омбіліческую катастрофу - як процес створення структур, схожих на волосяний покрив.

2.2.1. Гіперболічна омбіліка

V = x ³ + y ³ + a x y + b x + c y

2.2.2. Еліптична омбіліка

V = x ³ / ³ - x y ² + a (x ² + y ²⁾ + b x + c y

2.2.3. Параболічна омбіліка

V = y x ² + y ⁴ + a x ² + b y ² + c x + d y

3. Запис і класифікація катастроф по Арнольду

В. І. Арнольд запропонував класифікацію катастроф en: ADE classification, що використовує глибокі зв'язки з теорією груп Лі.

• A ₀ - несінгулярна точка: V = x .
• A ₁ - локальний екстремум : стійкий мінімум або нестійкий максимум .
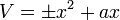• A ₂ - складка
• A ₃ - збірка
• A ₄ - ластівчин хвіст
• A ₅ - метелик
• A _k - нескінченна послідовність форм від однієї змінної
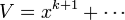
• D ₄ ⁺ - гаманець = гіперболічна омбіліка
• D ₄ ^{- -} піраміда = еліптична омбіліка
• D ₅ - параболічна омбіліка
• D _k - нескінченна послідовність інших омбілік
• E ₆ - символічна омбіліка V = x ³ + y ⁴ + a x y ² + b x y + c x + d y
• E ₇
• E ₈

У теорії сингулярності є об'єкти, які відповідають більшості інших простих груп Лі.

4.   Застосування теорії катастроф

Створення та розвиток цієї частини математичного аналізу було пов'язано з широкими можливостями наочного аналізу деяких складних явищ, особливо тих, які зустрічаються при описі самих різних природних явищ ( веселка, каустику, стійкість складних систем, коливання і руйнування в будівельній механіці, поведінку в етології, і навіть бунти в в'язницях).

Список використаної літератури

1.     Арнольд В. І. Теорія катастроф

2.     В. І. Арнольд. Особливості у варіаційному численні.

3.     В. І. Арнольд, В. С. Афраймовіч, Ю. С. Ільяшенко, Л. П. Шильников. Теорія біфуркацій.

4.     Арнольд В. І. Особливості каустик і хвильових фронтів, - М.: Фазісу, 1996.

5.     Голубицький М., Гійемін В. Стійкі відображення та їх особливості, - М.: Мир, 1977.

6.     Постон Т., Стюарт І. Теорія катастроф і її застосування, - М.: Мир, 1980.

7.     Том Р. Структурна стійкість і морфогенез, - М.: Логос, 2002.

8.     Брус Дж., Джіблін П. Криві і особливості: Геометричне введення в теорію особливостей, - М.: Мир, 1988.