Теорія порівнянь в задачах

ЗАСТОСУВАННЯ ТЕОРІЇ ПОРІВНЯНЬ

ПРИ РОЗВ'ЯЗУВАННІ

ОЛІМПІАДНИХ ТА ПРИКЛАДНИХ ЗАДАЧ

(матеріал для факультативних занять з математики 10 клас)

МОДУЛЬНА АРИФМЕТИКА

1. Означення порівняння за модулем

Порівняння в  математиці - співвідношення між двома цілими числами а і b, яке означає, що різниця а - b цих чисел ділиться на задане ціле число m (модуль порівняння).

Означення. Якщо цілі числа а і b такі, що їх різниця ділиться на натуральне число m , то кажуть, що а і b можна порівняти по модулю m).

Слово «модуль» (від латинського «modulus» - міра) застосовується в різних областях математики і її додатків; воно присвоюється числу, що має особливо важливе значення; наприклад, по відношенню до нього ведеться рахунок або вимір.

Порівнянність чисел а і b по модулю m записується так:

a ≡ b (mod m) або

Зрозуміло, що два числа порівняні по модулю m тоді і тільки тоді, коли вони дають при діленні на m однакові залишки, тобто належать до одного і того ж класу.

Наприклад,

27 ≡ 7 (mod 10), 78 ≡ 6 (mod 24), 6 ≡ 0 (mod 3), 25 ≡ - 1 (mod 13).

Поняття порівнянності чисел виявляється корисним при вирішенні багатьох задач.

Задача 1. Для яких натуральних чисел n число n² + 2 ділиться на 3,

тобто n² + 2 ≡ 0 (mod 3)?

Розв’язок.

Якщо n ≡ 0 (mod 3), то n² + 2 ≡ 2 (mod 3),

        » n ≡ 1 (mod 3),  » n² + 2 ≡ 0 (mod 3),

        » n ≡ 2 (mod 3),  » n² + 2 ≡ 0 (mod 3),

Отже, n² + 2 ≡ 0 (mod 3) тоді і тільки тоді, коли n не ділиться на 3.

        Задача 2. Який залишок при діленні на 3 дає число

 (2² + 1) (3² + 1) (4² + 1) ... (1000² + 1)?

Розв’язок. Цей залишок не зміниться, якщо кожне з чисел 2, 3, . . . , 1000 в даному виразі замінити його залишком при діленні на 3. Таким чином, число по модулю 3 дорівнює

(2³ + 1)³³³ (3³ + 1)³³³ (1³ + 1)³³³ ≡ 5³³³ × 10³³³ × 2³³³ ≡ 2³³³ × 1³³³ × 2³³³ ≡ 4³³³ ≡ 1³³³ 1, тобто, шуканий залишок дорівнює 1.

3адача 3. Довести, що всяке натуральне число n порівняно по модулю 9 зі своєю сумою цифр.

Рішення. Нехай

a = anan-1…a0,

де a₀ a₁…, a_n – цифри числа а. Маємо

a = a_n ∙ 10ⁿ + a_n-1 ∙ 10^n-1 + … + a₀

Запишемо тепер наступні очевидні порівняння:

1 ≡ 1 (mod 9), 10 ≡ 1 (mod 9), ... 10ⁿ ≡ 1 (mod 9)

Премножаючи  ці порівняння відповідно на a₀ , a₁ , …, a_n і складаючи, отримуємо

a₀ + 10 ∙ a₁ + … + 10ⁿa_n = a (a₀ + a₁ + … + a_n ) (mod 9)

Звідси, до речі, відразу виходить відома ознака подільності чисел на 9 (і на 3).

2. Основні властивості порівнянь за модулем

Порівняння мають багато властивостей, аналогічних властивостям математичної рівності.

Наприклад, доданок можна переносити з протилежним знаком з однієї частини порівняння в іншу; обидві частини порівняння можна множити на одне й те саме число; обидві частини порівняння можна ділити на спільний дільник n лівої і правої частин, але при цьому модуль нового порівняння дорівнюватиме m/k, де m - модуль попереднього порівняння, k - найбільший спільний дільник чисел m і n.

Порівняння з однаковим модулем можна почленно додавати, віднімати і перемножувати.

Розглянемо детальніше основні властивості.

Якщо а ≡ b (mod m), і c ≡ d (mod m), то а + c ≡ b + d (mod m),

a - c ≡ b - d (mod m), ac ≡ bd (mod m).

Доведемо, наприклад, що порівняння можна перемножувати.

Так як a ≡ b (mod m) і c≡ d (mod m), то a - b та с - d діляться на m.

З рівностей ас - bd ≡ас - ad + ad - bd ≡a (c - d) + d (a - b)видно, що ас - bd також ділиться на m, тобто ac≡ bd (mod m).

В якості вправи доведемо, що порівняння можна додавати і віднімати.

Нехай a≡ b (mod m). Із зазначених вище властивостей порівнянь випливає, що aⁿ≡ bⁿ (mod m) для будь-якого натурального k (тобто що обидві частини порівняння можна підносити до степеня) і, крім того, що ac≡ bc (mod m), де с - будь-яке ціле число (тобто що обидві частини порівняння можна помножити на будь-яке ціле число).

У теорії чисел розглядаються методи розв'язування різних порівнянь, тобто методи відшукування цілих чисел, які задовольняють порівняння того чи іншого виду.  Якщо число  х є розв'язком порівняння за модулем m, то будь-яке число виду х + km (k — ціле число) також є розв'язком цього порівняння. Сукупність чисел виду х + km (k =…, -2, -1,0, 1,2, …) називають класом за модулем m. Поняття порівняння для цілих чисел можна узагальнити, а саме: можна говорити про порівнянність двох елементів кільця за ідеалом.

Перелічимо далі деякі властивості порівнянь, схожі на властивості рівнянь.

Властивість 1. Порівняння за однаковим модулем можна почленно додавати.

Властивість 2. Доданок, що стоїть в якій-небудь частині порівняння, можна переносити в іншу частину, змінивши його знак на зворотний.

Властивість 3. До будь-якої частини порівняння можна додати будь-яке число, кратне модулю.

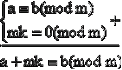
.Властивість 4. Порівняння за однаковим модулем можна почленно перемножувати.

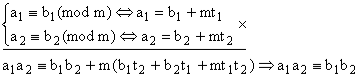
Властивість 5. Обидві частини порівняння можна піднести до однакового степеня.

Властивість 6. Обидві частини порівняння можна поділити на їхній спільний дільник, взаємно простий з модулем.

Властивість 7. Обидві частини порівняння і його модуль можна помножити на те саме ціле число або розділити на їхній спільний дільник.

Властивість 8. Якщо порівняння  a ≡  b  існує за кількома різними модулями, то воно існує й за модулем, що дорівнює найменшому спільному кратному цих модулів.

Властивість 9. Якщо порівняння існує за модулем m, то воно існує і за модулем d, що дорівнює будь-якому дільнику числа m.

Властивість 10. Якщо одна частина порівняння і модуль діляться на деяке число, то й інша частина порівняння мусить ділитися на те ж число.

В теорії порівнянь є важливі теореми, які успішно можна використовувати при розв’язуванні задач.

Теорема Єйлера. Якщо (a,m) =1, то a ^f(m) ≡ 1(mod m) .

Теорема Ферма. Якщо (a, р) =1, то a ^р-1 ≡ 1(mod р) .

3. Різні методи розв’язування олімпіадних задач за допомогою порівнянь

 Задачі на знаходження остач від ділення на число

Задача 1. Знайти остачу від ділення 1999²⁰⁰⁰ на 5.

Розв’язок.

Щоб розв’язати таку задачу, слід привести вираз до порівняння за модулем m з 1 або –1. Оскільки 1999 : 5 = 399 (ост. 4),

1999²⁰⁰⁰ ≡   4²⁰⁰⁰ = 16¹⁰⁰⁰ ≡ 1¹⁰⁰⁰ = 1. 1 – остача. Відповідь: 1.

Задача 2. Довести, що 11ⁿ⁺²+12^{2 n +1} ділиться на 133 без остачі.

Розв’язок

Перший спосіб. Доведення методом індукції

При

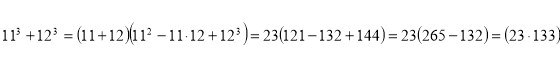
При  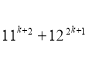 ;ділиться на 133

При

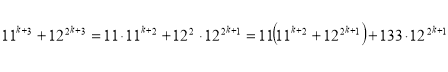
ділиться на 133;

Що і треба було довести.

Другий спосіб. Доведення за допомогою порівнянь.

Виконаємо елементарні перетворення і доведемо це твердження:

11ⁿ⁺²+12²ⁿ⁺¹  = 11ⁿ∙121+12^{2 n} ∙12= 11ⁿ ∙121+12^{2 n} ∙12+12∙11ⁿ –12∙11ⁿ

= 133∙11ⁿ +12∙ (144ⁿ–11ⁿ)

12∙  (144ⁿ–11ⁿ) ≡ 12∙  (11ⁿ  –11ⁿ) = 0.

Задача 3. Знайти остачу від ділення 520 на 24.

Використовуємо властивості порівнянь і отримуємо: 25 ≡ 1 (mod 24);

52 ≡ 1 (mod 24);

(52)10 ≡ 110 (mod 24);

520 ≡ 1 (mod 24).

Задача 4. Знайти остачу від ділення числа 5403 на 101.

101 – просте число. Числа 5 и 101 взаємно прості, а тому з теореми Ферма випливає, що

5100 ≡1(mod 101) .

Піднесемо це порівняння почленно у четверту степінь. Отримуємо:

5400 ≡1(mod 101) .

Крім того, 53 ≡ 24(mod101). Перемножуємо ці порівняння:

5403 ≡ 24(mod 101) .

З остатнього порівняння випливає, що остача це число 24.

 Задачі на доведення подільності на число

Задача 1. Довести, що для будь-якого натурального n число

37n+2 + 16n+1 + 23n ділиться на 7.

Рішення. 

Оскільки 37 ≡ 2 (mod 7), то 37ⁿ⁺²≡ 2ⁿ 4 (mod 7); 16 ≡ 2 (mod 7), то 16ⁿ+1≡ 2ⁿ 2 (mod 7);

23≡ 2 (mod 7), то 23ⁿ ≡ 2ⁿ (mod 7);

Піднесемо перше порівняння до степеня n+2, друге – до степеня n+1, третє – до степеня n і додамо:

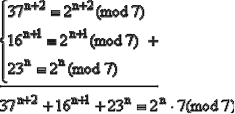
Доведення якогось твердження про остачу частіше всього зводиться до знаходження остачі.

Задача 2. Довести, що при будь-якому цілому n числа n(n2+5) діляться без остачі на 6.

Розв’язок. Будь-яке ціле число n при діленні на 6 дає в остачі 0, 1, 2, 3, 4 або 5. Результати порівняння за модулем 6 зведемо в наступну таблицю.

n	0	1	2	3	4	5
n2	0	1	4	9	16	25
n2+5	5	6	9	14	21	30
n(n2+5)	0	6	18	52	84	150

 

Як бачимо, числа останнього рядочку таблиці діляться без остачі на 6. Отже, n(n2+5) ділиться без остачі на 6.

Задача 3.Довести, що (4n + 15n - 1) ділиться на 9, якщо n належіть N

Розв’язок. Для доведення використаємо метод математичної індукції та порівнянь за модулем.

Доведемо, що (4n + 15n - 1) ділиться на 9 методом математичної індукції.

При n = 1, 4n + 15n - 1 = 4 + 15 - 1 = 18, ділиться на 9. Перевірено.

Перехід:

Нехай (4n + 15n - 1) виконується при n = k. Доведемо, що воно виконується при n = k + 1:

4k +1 + 15(k + 1) - 1 = 4 · 4k + 15k - 14 = 4k + 15k - 1 + 3 · 4k + 15.

За умовою переходу 4k + 15k - 1 ділиться на 9, треба показати, що 3 · 4k + 15 ділиться на 9. Звертаємо увагу на те, що 3 · 4k + 15 = 3(4k + 5) . До цього

4 ≡ 1 (mod 3);

4k ≡ 1 (mod 3);

4k + 5 ≡ 6 (mod 3), що показує, 4k + 5 ділиться на 3, а 3 · 4k + 15 = 3(4k + 5) на 9.

Перехід доведено, тому (4n + 15n - 1) ділиться на 9.

Прикладні задачі

Задача 1. Як скласти розклад турніру?

Припустимо, в спортивному змаганні беруть участь N команд і для виявлення переможця кожна з них повинна зіграти по одній грі з кожною іншою командою. Бажано скласти розклад турніру так, щоб у команд не було зайвих «простоїв». І в цьому нам допоможе теорія порівнянь.

Домовимося вважати число N парним. Якщо це не так, то додамо одну фіктивну команду - «гра» з нею буде прирівнюватися для кого до вимушеного, а для кого до заслуженого відпочинку. Кожній команді присвоїмо номер в турнірній таблиці: х. = 1, 2, ..., N - 1, N.

Розглянемо перші N - 1 команд. В якості партнера команди з номером х призначимо в r - му турі (r= 1, 2, ..., N - 1) команду з номером у, що задовольняє умовам

Збіг номерів х і у при виконанні порівняння х + у = r (mod(N – 1)) можливо тільки в тому випадку, якщо 2x = r (mod(N – 1)). А це, у свою чергу, можливо, коли x = при парному r, x = При непарному r.

В такому випадку для команди х в якості партнера призначимо команду з номером N.

Так будуть виконані всі необхідні умови турніру:

1.В одному турі різні команди мають партнерів.

2.Кожна команда в різних турах грає з різними партнерами.

3.По завершенні N -1 туру кожна команда грає з кожною.

Ось так виглядає турнірна таблиця для шести учасників.

r x  r	11	22	33	44	55	66
11	55	44	66	22	11	33
22	66	55	44	33	22	11
33	22	11	55	66	33	44
44	33	66	11	55	44	22
55	44	33	22	11	66	55

На перетині r-го рядка і x-го стовпчика стоїть номер партнера, з яким команда x грає в r-му турі.

Задача 2. Фішка ходить по дошці N x N, зрушуючи на 1 клітину вгору, вправо або вниз-вліво по діагоналі. Чи може фішка обійти всі клітини дошки по разу і закінчити шлях зверху від початкової клітини.

Розв'язання : Підберемо розмальовку, при якій фішка буде однаково міняти колір при будь-якому ході. Просто шахова і "матрац" не підійдуть. А зате шахова розмальовка в 3 кольори - просто чудово Наша фішка буде ходити з червоного на жовтий, з жовтого на зелений, з зеленого на червоний і т.д. Нехай, скажімо, початкова клітина червона - тоді кінцева буде жовта. Кольори чергуються по циклу довжини 3, тому число ходів: 3k +1 (тобто = 1 по mod 3). Але те ж число ходів на дошці NxN одно N2 -1. Звідси N 2 = 2 (mod 3), чого, з міркувань теорії чисел не буває.

Відповідь "не можна".