Тест "Паралельність прямих і площин у просторі"

Контрольний тест за темою

«Паралельність прямих і площин у просторі»

Завдання 1 – 24 дати однозначну відповідь «так» чи  «ні»;                   завдання 25 – 33 обрати одну правильну відповідь; завдання                           34-37 розв’язати і записати відповідь.

1. Якщо  ||  , то будь-яка пряма площини  паралельна площині .

2. Якщо  || , то будь-яка пряма площини  паралельна кожній прямій площини .

3. Якщо || , то будь-яка пряма площини  мимобіжна кожній прямій площини .

4. Якщо || , то для будь-якої прямої а площини  існує пряма  b в площині  така, що а || b.

5. Якщо  || , то для будь-якої прямої а площини  існує пряма  b в площині  така, що прямі а і b — мимобіжні.

6. Якщо  || , то будь-яка пряма, яка перетинає площину , перети­нає і площину  .

7. Якщо || , то будь-яка пряма, яка паралельна площині , пара­лельна і площині .

8. Якщо дві прямі площини  паралельні відповідно двом прямим площини , то  || .

9. Якщо деяка пряма площини  паралельна площині , то  || .

10. Якщо кожна пряма площини  паралельна площині , то  || .

11. Якщо дві прямі, одна з яких лежить у площині  , а друга — в площині , не мають спільних точок, то  || .

12. Якщо кожні дві прямі, одна з яких лежать у площині, а дру­га — в площині, не мають спільних точок, то  || .

13. У даній площині лежить тільки одна сторона трапеції. Чи вірно, що одна зі сторін трапеції паралельна даній площині?

14. Чи вірно, що середня лінія трикутника паралельна  будь-якій площині, що проходить через сторону цього трикутника, паралельно середній лінії?

15. Чи будуть рівні два паралельних відрізки, які утворені між паралельними площинами?

16. У площині нескінченно багато прямих, паралельних іншій площині. Чи вірно, що ці дві площини паралельні?

17. Дві сторони паралелограма паралельні площині. Чи вірно, що ця площина й площина паралелограма паралельні?

18. Відомо, що пряма паралельна площині. Чи існують у площині прямі, які не паралельні даній прямій?

19. Чи може площина, що проходить через середини двох сторін трикутника, перетинати його третю сторону?

20. Чи можуть прямі, які паралельні одній площині, бути мимобіжними?

21. Чи завжди можна через дану точку провести пряму, яка паралельна двом даним площинам (точка не належить жодні з них)?

22. Чи вірно, що дві прямі, які паралельні одній й тій же площині, паралельні між собою?

23. Чи вірно, що дві площини, які паралельні одній й тій же прямій, паралельні між собою?

24. Чи може пряма перетинати одну з паралельних площин, а іншій бути паралельною?

25.  Пряма а паралельна площині α. Скільки площин, паралельних площині α, можна провести через пряму а?

А) Одну;     Б) дві;      В) жодної;     Г) безліч.

26.  Як розташовані площини α і β, якщо пряма а перетинає площину α і паралельна площині β?

А) Паралельні;           Б) перетинаються;

В) збігаються;    Г) визначити не можливо.

27.  Площини α і β паралельні. Пряма а перетинає площину α. Як розташована пряма а відносно площини β?

А) Паралельна площині;     Б) лежить у площині;

В) перетинає площину ;              Г) визначити не можливо.

28.  Яке з наведених тверджень неправильне?

А) Для будь-яких двох прямих можна провести площину, паралельну кожній із них;

Б) дві площини обов'язково паралельні, якщо дві прямі, що лежать в одній площині, відповідно паралельні двом прямим, що лежать в іншій площині;

В) усі прямі, які проходять через одну точку, паралельно заданій площині, лежать в одній площині;

Г) через пряму, паралельну заданій площині,  можна провести площину, паралельну даній, і до того ж тільки одну.
 

29.  Яке з наведених тверджень неправильне?

А) Дві площини паралельні, якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом прямим, що перетинаються, другої площини;

Б) через будь-яку точку поза заданою площиною можна провести площину, паралельну заданій, і до того ж тільки одну;

В) якщо пряма перетинає одну з двох площин, що перетинаються, то вона обов'язково перетинає і другу площину;

Г) дві площини, паралельні третій площині, паралельні між собою.

30.  Дано куб МNKLМ₁N₁K₁L₁ (рис. 1). Укажіть площину, пара­лельну площині МКN₁.

А)МКN₁; Б)М₁К₁L; В)М₁К₁N;   Г)NLN₁.

Рис. 1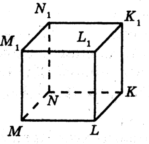    

31.  Дві сторони трикутника паралельні площині . Як розміще­на відносно площини медіана трикутника, яка проходить між цими сторонами?

А ) Має з спільну точку;       Б) Лежить у площині;

В) Паралельна площині ;       Г) Інша відповідь.

32.  Відрізок АВ не перетинає площину α, С — середина відрізка АВ. Через точки А, В, С проведені паралельні прямі, які перетинають площину α  відповідно в точках А₁, В₁, С₁. Знайдіть АА₁,  якщо ВВ₁ = 4 CM; CC₁ = 3 см.

А) 1 см;       Б) 2 см;    В) 3 см;    Г) 4 см.
 

33.  Дано дві паралельні площини α і β. Точки А і В належать площині α, точки С і D — площині β. Відрізки AD і ВС перетинаються в точці М, АВ = 10 см, BM = 6 см, CM = 12 см. Знайти довжину відрізка CD.

34. Паралельні площини і перетинають сторони кута В
у точках А₁С₁і А₂С₂відповідно (рис. 2). Знайдіть довжину відрізка ВС₂, якщо А₁С₁:А₂С₂ = 1:5і ВС₁=2 см.

Рис.2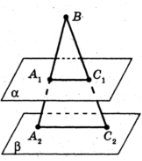 

35.  Площина α і β паралельні між собою. Точка С не належить жодній із площин  і не лежить між ними. Через цю точку проведено  дві прямі. Одна з них перетинає площини α і β у точках А₁ і В₁, а друга - у точках А₂ і В₂ відповідно. Знайдіть довжину відрізка  А₁А₂,  якщо СВ₁=m,  А₁В₁=n,  В₁В₂=k  і CА₂<CB₂.

36. Дано дві паралельні площини і . Точки А і Влежать у площині, точки С і D — у площині . Відрізки АD і ВС перетинаються в точці М. Знайдіть довжину відрізка АВ, якщо СD = 4 см, ВМ: СМ = 2:1.

Відповіді: