ТЕСТ «ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ У ПРОСТОРІ. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМОЇ І ПЛОЩИНИ»

тест                                                                                                                «ПерпендикулярніСТЬ прямИХ у просторі.                                          Перпендикулярність прямої і площини»                                                                   

Варіант І  

1. Яке твердження правильне?

1) Якщо одна з двох прямих перпендикулярна до третьої прямої, то і друга пряма перпендикулярна до цієї прямої.

2) Якщо дві прямі перпендикулярна до третьої прямої, то вони паралельні.

3) Якщо дві прямі перпендикулярні до площини, то вони паралельні.

2. Пряма m перпендикулярна до прямих a і b, які лежать в площині , але m не перпендикулярна до площини . Тоді прямі a і b…

1) паралельні;

2) перетинаються;

3) мимобіжні.

3. Площина проходить через вершину А ромба ABCD перпендикулярно до діагоналі АС. Тоді діагональ BD…

1) перпендикулярна до площини ;

2) паралельна до площини ;

3) лежить в площині

4. Тоді  прямі a і b не можуть  бути…

1) мимобіжними;

2) перпендикулярними;

3) паралельними.

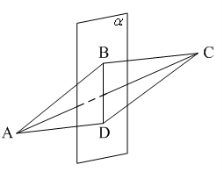
5. ABCD – паралелограм, Тоді  ABCD не може бути…

1) прямокутником;

2) квадратом;

3) ромбом.

6. Пряма перпендикулярна площині круга, якщо вона перпендикулярна двом …

1) радіусам;    

2) діаметрам;    

3) хордам.

Варіант ІІ

1. Пряма називається перпендикулярною до площини, якщо вона перпендикулярна…

1) до однієї прямої, що лежить у площині;

2) до двох прямих, що лежать у площині;

3) до любої прямої, що лежать у площині.

2. . Тоді прямі a і b не можуть бути …

1) перпендикулярними;

2) паралельними;

3) мимобіжними.

3. Діагональ АС квадрата ABCD перпендикулярна  до деякої площини , яка проходить через точку А. Тоді діагональ BD…

1) перпендикулярна  площині ;

2) паралельна площин і ;

3) лежить у площині .

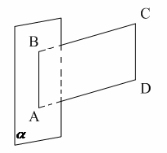
4. ABCD – паралелограм, Тоді ABCD не може бути…

1) ромбом;

2) квадратом;

3) прямокутником.

5. Прямі b і с не можуть  бути…

1) паралельними;

2) перпендикулярними;

3) мимобіжними.

6. Яке твердження неправильне?

1) Через будь-яку  точку простору проходить пряма, яка перпендикулярна до даної площини, і тільки одна.

2) Через точку, що не лежить на прямій можна побудувати тільки одну площину, перпендикулярну даній прямій.

3) Через точку, не лежить на даній прямій, можна побудувати тільки одну пряму, перпендикулярну даній прямій.

ВІДПОВІДІ: