Урок "Кути в просторі"
- в просторі.docx docx
- 75-76 Кути в просторі.pptx pptx
І– й курс
Заняття №
_________
Тема Кути в просторі.
Мета
Навчальна: ввести поняття кутів в просторі, кут між прямою і площиною, кут між похилою і площиною, кут між площинами, навчитися знаходити кути в просторі та розрізняти їх.
Розвиваюча: розвивати логічне мислення, уяву, пам'ять.
Виховна: виховувати математичну культуру, відповідальність.
Основні поняття: кут, простір, похила, перпендикуляр, площина, пряма, проекція.
Очікуванні результати: вивчені поняття та застосування їх на практиці.
Студенти знатимуть: розташування кутів в просторі, знаходження кутів між площинами та прямими.
Студенти вмітимуть: розрізняти розміщення кутів, знаходити міри кутів в просторі, будувати різні види розміщення кутів в просторі.
Тип заняття: засвоєння нових знань і вмінь.
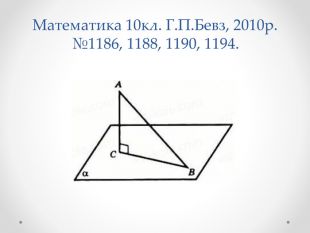
Література: Математика 10кл. Г.П.Бевз, 2010р.
Хід заняття.
- Організаційна частина.
- Перевірка домашнього завдання.
Вивчити конспект.
Виконати № 1108, 1110, 1112.
- Актуалізація опорних знань.
Дати відповіді на питання:
- Що називається проектуванням?
- Яка проектування вам відоме?
- Чим відрізняється паралельне проектування і ортогональне?
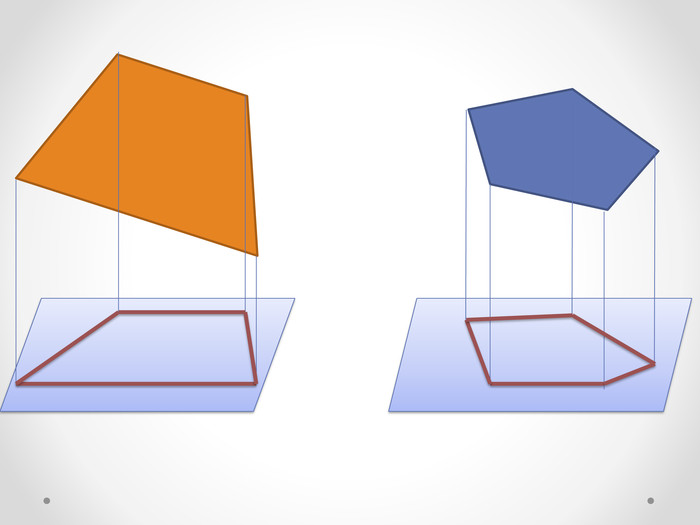
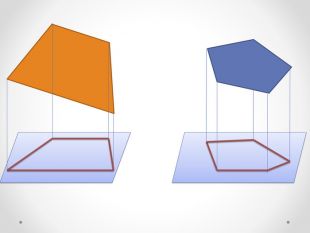
- Зобразіть ортогональне проектування даної фігури:
![]()
![]()
![]()
![]()

![]()

![]()
![]()
- Вивчення нового матеріалу.
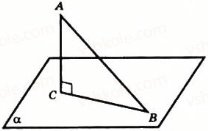
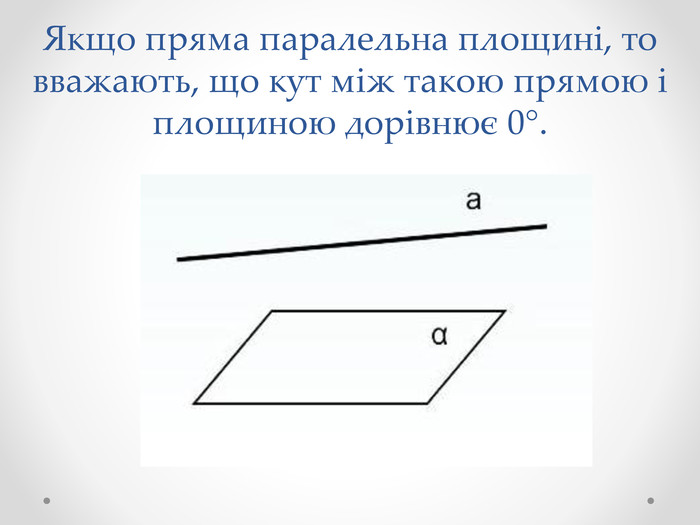
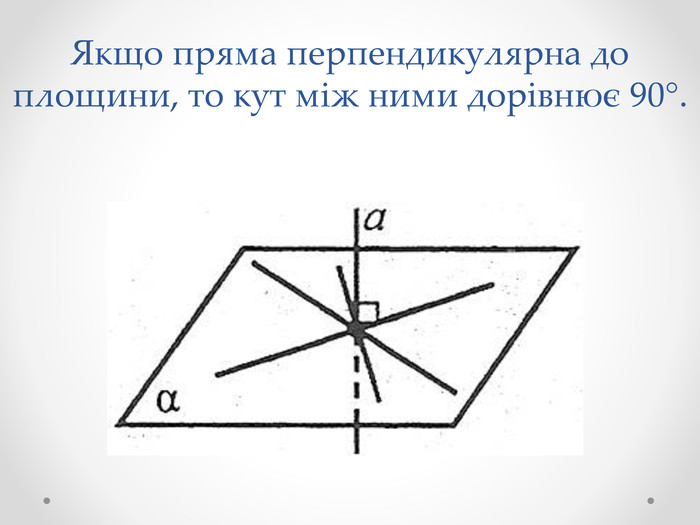
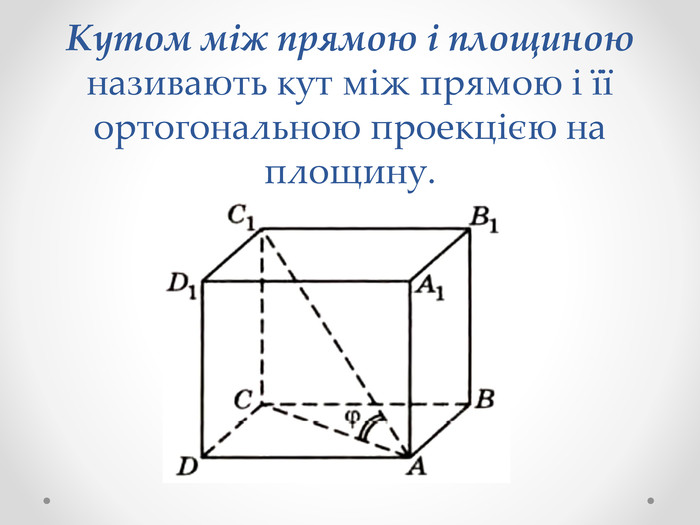
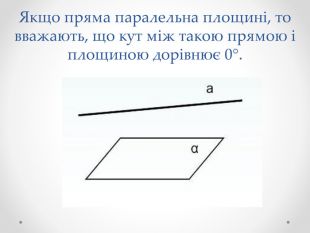
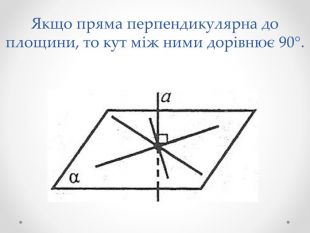
 Якщо пряма паралельна площині, то вважають, що кут між такою прямою і площиною дорівнює 0°. Якщо пряма перпендикулярна до площини, то кут між ними дорівнює 90°. У решти випадків кутом між прямою і площиною називають кут між прямою і її ортогональною проекцією на площину.
Якщо пряма паралельна площині, то вважають, що кут між такою прямою і площиною дорівнює 0°. Якщо пряма перпендикулярна до площини, то кут між ними дорівнює 90°. У решти випадків кутом між прямою і площиною називають кут між прямою і її ортогональною проекцією на площину.
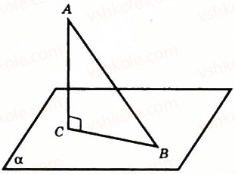
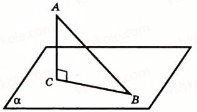
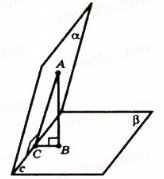
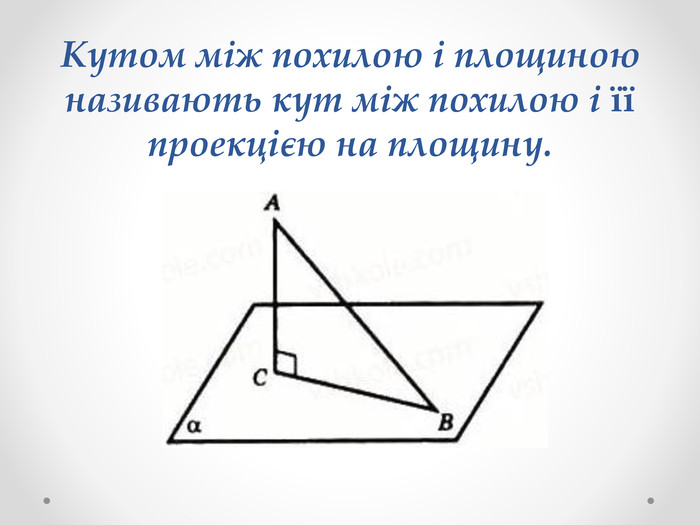
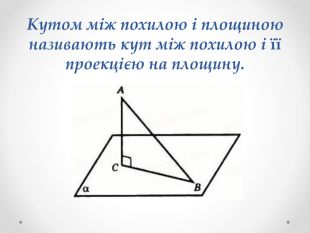
Кутом між похилою і площиною називають кут між похилою і її проекцією на площину. Йдеться про прямокутну (ортогональну) проекцію. Кут між похилою і площиною найменший з усіх кутів, які похила утворює з прямими, проведеними на площині через основу похилої.
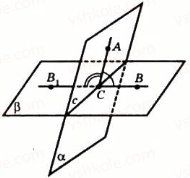
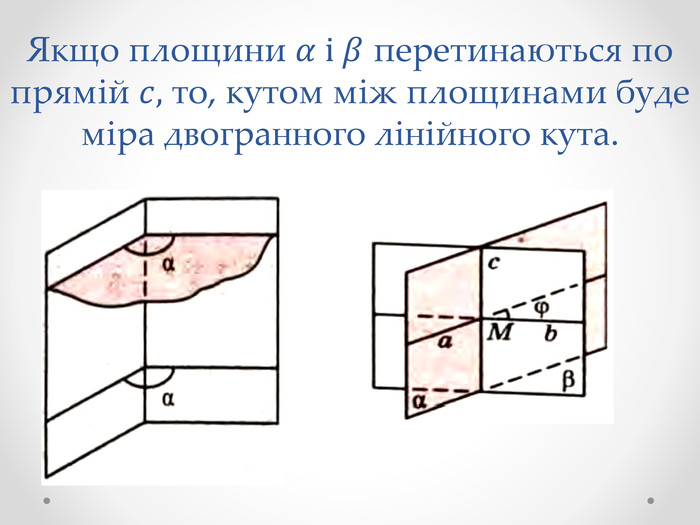
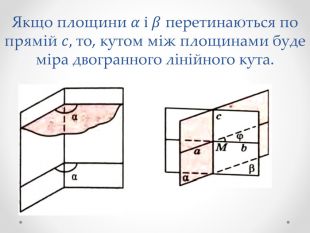
Кут між площинами. Якщо дві площини паралельні, то вважається, що кут між ними дорівнює 0°. Якщо площини ![]() перетинаються по прямій
перетинаються по прямій ![]() то, щоб визначити
то, щоб визначити 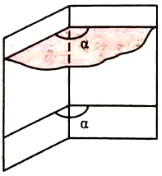 кут між цими площинами, у кожній з них через довільну точку
кут між цими площинами, у кожній з них через довільну точку ![]() прямої
прямої ![]() можна провести прямі
можна провести прямі ![]() , перпендикулярні до прямої
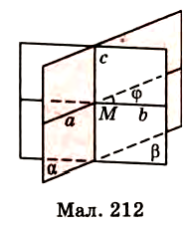
, перпендикулярні до прямої ![]() (мал. 212). Кут між прямими
(мал. 212). Кут між прямими ![]() приймають за кут між даними площинами
приймають за кут між даними площинами ![]() . Можна довести, що міра цього кута
. Можна довести, що міра цього кута ![]() не залежить від вибору точки О на прямій
не залежить від вибору точки О на прямій ![]() Кут між двома площинами, як і між двома прямими, знаходиться в межах від 0° до 90°.
Кут між двома площинами, як і між двома прямими, знаходиться в межах від 0° до 90°.
Якщо кут між двома площинами дорівнює 90°, то площини перпендикулярні.
- Закріплення вивченого матеріалу.
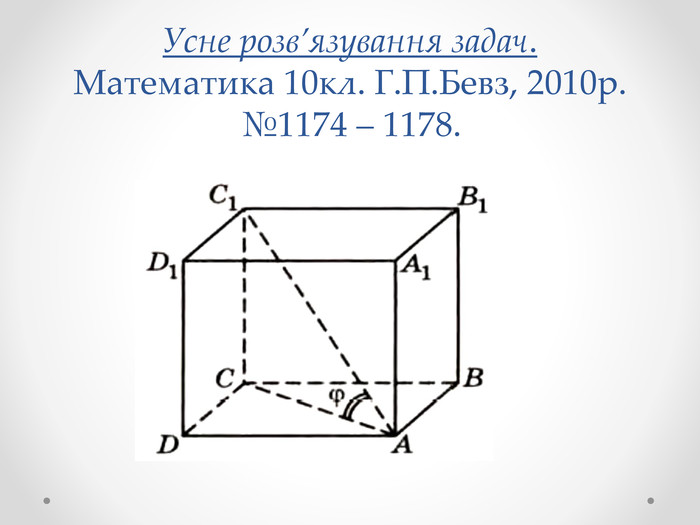
Усне розв’язування задач.
Математика 10кл. Г.П.Бевз, 2010р. №1174 – 1178.
№1174. Чи може бути від’ємним косинус кута нахилу похилої до площини?
1174. Ні. Так як ![]() , то
, то ![]()
![]() – кут нахилу похилої до площини.
– кут нахилу похилої до площини.
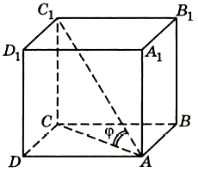
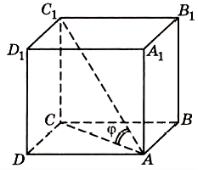 №1175. На малюнку
№1175. На малюнку ![]() діагональ куба
діагональ куба ![]() Під яким кутом нахилена діагональ куба до кожної його грані?
Під яким кутом нахилена діагональ куба до кожної його грані?
1175. Нехай ребро кута дорівнює ![]()
тоді ![]()
З ![]()
![]()
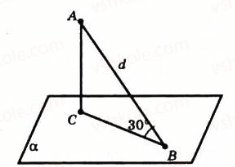 №1176. Похила
№1176. Похила ![]() завдовжки
завдовжки ![]() нахилена до площини а під кутом 30°. Знайдіть відстань від точки
нахилена до площини а під кутом 30°. Знайдіть відстань від точки ![]() до площини
до площини ![]() .
.
1176. ![]() за властивістю катета, який лежить проти кута
за властивістю катета, який лежить проти кута ![]() .
. ![]()
Відповідь: ![]()
№1177. Чи правильно, що дві непаралельні площини ділять простір на чотири двогранні кути?
Так.
№1178. Кут між двома площинами дорівнює 100°. Укажіть міру меншого з утворених двогранних кутів.
1178. ![]()
Відповідь: ![]()
Математика 10кл. Г.П.Бевз, 2010р. №1186, 1188, 1190, 1194 .
№1186. Похила вдвічі довша за її проекцію на площину. Знайдіть кут між похилою і площиною.
|
|
1186. Нехай
З
Відповідь: |
№1188. Знайдіть кут між похилою і площиною, якщо вершина похилої віддалена від площини на відстань, що дорівнює довжині проекції похилої.
|
|
1188. Нехай
Так як
тоді
Відповідь: |
№1190. Довжина похилої ![]() дорівнює 50 см, а точка
дорівнює 50 см, а точка ![]() віддалена від площини на 25 см. Знайдіть кут між похилою і площиною.
віддалена від площини на 25 см. Знайдіть кут між похилою і площиною.
|
|
1190. Нехай
З
Відповідь: |
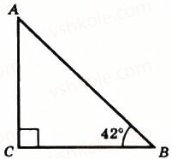
№1194. На якій глибині знаходиться станція метро, якщо її ескалатор довжиною 85м нахилений до площини горизонту під кутом 42°?
|
|
1194. Нехай
Знайдемо
З
|
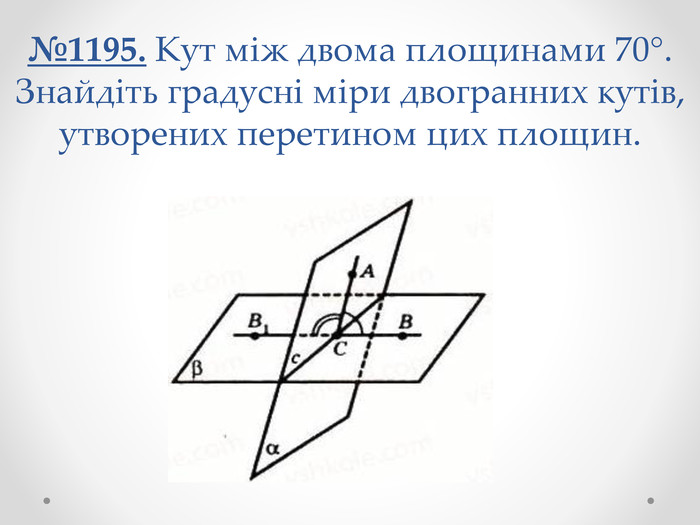
№1195. Кут між двома площинами 70°. Знайдіть градусні міри двогранних кутів, утворених перетином цих площин.
|
|
|
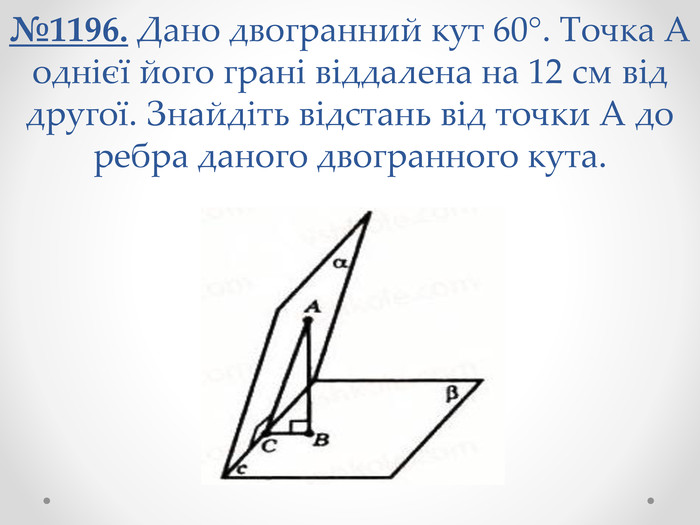
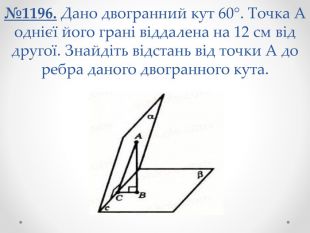
№1196. Дано двогранний кут 60°. Точка А однієї його грані віддалена на 12 см від другої. Знайдіть відстань від точки А до ребра даного двогранного кута.
|
|
|
- Підведення підсумків.
- Що таке кут? Які бувають кути?
- Що таке кут між прямою і площиною?
- Яким може бути кут між прямою і площиною?
- Що таке кут між похилою і площиною?
- Що таке кут між двома площинами?
- Якими приладами вимірюють кут між прямою і горизонтальною площиною?
- Що таке двогранний кут? Які бувають двогранні кути?
- На скільки двогранних кутів розбивають простір дві непаралельні площини?
- Що таке лінійний кут двогранного кута?
- Який з двох двогранних кутів більший?
- У яких межах може змінюватися міра двогранного кута?
- Домашнє завдання.
- Вивчити конспект.
- Виконати № 1187, 1189, 1197.
1


про публікацію авторської розробки
Додати розробку