Навчальний посібник "Медіана трикутника"
 Навчально-виховний комплекс
Навчально-виховний комплекс
«Загальноосвітня школа І-ІІІ ступеня №1 – гімназія
імені Героя Радянського Союзу В.Газіна» смт Ратне
Ратнівського району Волинської області
Т.Сілянкова, Н.Кіпень
Медіана трикутника
Навчальний посібник
Ратне - 2019
ЗМІСТ
ВСТУП………………………………………………………………….……..…4
РОЗДІЛ І. Теоретичні відомості про медіану трикутника……...……….…6
- Означення і властивості медіани трикутника……………...……………..6
- Медіана у рівнобедреному трикутнику……………………...…………..13
- Медіана у прямокутному трикутнику…………………………………..15
РОЗДІЛ ІІ. Властивість одна – способи доведення різні….……………….16
РОЗДІЛ ІІІ. Метод подвоєння медіани……………….…………….………..23
РОЗДІЛ ІV. Медіана в олімпіадних задачах…………………...……………27
РОЗДІЛ V. Задачі для самостійного розв’язування…………..……………31
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ………………...…………………..34
ВСТУП
Сучасному світу потрібна людина з широким кругозором, міцними знаннями, яка добре володіє технічними науками та вміє знаходити раціональні шляхи вирішення проблем. А це означає, що зростають вимоги до вивчення математики.
А як навчитися розв’язувати задачі? Як здати ДПА і ЗНО без проблем?
По-перше, необхідні міцні знання теоретичної бази. Медіана трикутника – це важлива, захоплива і цікава тема в планіметрії. Проте сучасна шкільна програма не розглядає ряд основних властивостей цієї чудової лінії трикутника. У цьому посібнику детально висвітленні теоретичні відомості з темі «Медіана трикутника». Однак, відмінних знань теорії недостатньо для швидкого знаходження раціонального способу розв’язування задач. Цей посібник містить 14 різних способів доведення однієї із властивостей медіани прямокутного трикутника, що дає можливість повторити теоретичний матеріал шкільного курсу планіметрії та вибрати найоптимальніші способи доведення. Це дасть можливість учителям та учням відпрацювати навички з тем: «Кути, утворені за перетину паралельних прямих січною», «Сума кутів трикутника», «Рівнобедрений трикутник», «Прямокутний трикутник», «Ознаки рівності трикутників», «Паралелограм», «Кути, вписані в коло», «Середня лінія трикутника», «Теорема Фалеса», «Теорема Піфагора», «Теорема косинусів», «Координати на площині», «Вектори на площині», «Геометричні перетворення».
У посібнику розглянуто спосіб подвоєння медіани трикутника, що значно спрощує розв’язування ряду задач. Також посібник містить 27 доведених властивостей і розв’язаних задач, у тому числі завдання математичних олімпіад різних рівнів. Ще 25 завдань пропонуються для самостійного розв’язування. До них наведені відповіді.
Посібник покликаний допомогти вчителю у проведенні урочної та позаурочної роботи з учнями, розширити їх математичний кругозір, підготуватися до шкільних занять, до участі в різноманітних математичних змаганнях, до успішної здачі ДПА та ЗНО.
Сподіваємося, що запропонований вашій увазі посібник допоможе читачу зануритися в захопливий світ геометрії й сприятиме успішному розв’язанню задач з теми «Медіана трикутника».
РОЗДІЛ І. Теоретичні відомості про медіану трикутника
-
 Означення і властивості медіани трикутника
Означення і властивості медіани трикутника
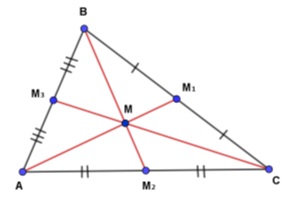
Медіаною трикутника називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
На малюнку відрізок АМ1 — медіана трикутника АВС. Точку М1 називають основою медіани. Будь-який трикутник має три медіани. Відрізки АМ1, ВМ2 і СМ3 — медіани трикутника. Медіани трикутника АВС із сторонами а, b, с прийнято позначати mа, mb, mс. З вершини А виходить медіана mа, з вершини В виходить медіана mb, з вершини С виходить медіана mс.. У будь-якому трикутнику три медіани перетинаються в одній точці. Ця точка називається центроїдом трикутника або центром мас.
Властивості медіан трикутника
Медіани рівних трикутників, проведені до відповідно рівних сторін, рівні.
Доведення
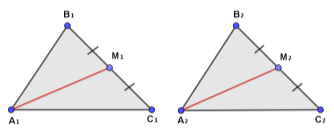 Нехай ∆А1В1С1 = ∆А2В2С2.
Нехай ∆А1В1С1 = ∆А2В2С2.
А1М1, А2М2 – медіани трикутників, проведені до сторін В1С1, В2С2, відповідно. Розглянемо ∆А1М1С1 і ∆А2М2С2:
1) А1С1 = А2С2 (як відповідні сторони рівних трикутників),
2) М1С1 = М2С2 (як половини відповідних сторін рівних трикутників),
3) ![]() С1 =
С1 = ![]() С2 (як відповідні кути рівних трикутників).
С2 (як відповідні кути рівних трикутників).
Отже, ∆А1В1С1 = ∆А2В2С2 за двома сторонами і кутом між ними. З рівності трикутників маємо А1М1 = А2М2. Що і потрібно було довести.
Властивість 2.
Медіана трикутника рівновіддалена від вершин В і С трикутника АВС.
Доведення
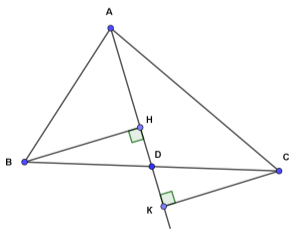 Проведено перпендикуляри ВН і СК до медіани AD. Розглянемо трикутники BDH і CKD. Ці трикутники прямокутні: кути CKD і BHD прямі. Кути CDK і BDH рівні за гіпотенузою та гострим кутом. Якщо трикутники рівні, то рівні і їх відповідні сторони: ВН=СК. Отже, вершини В і С рівновіддалені від медіани AD.
Проведено перпендикуляри ВН і СК до медіани AD. Розглянемо трикутники BDH і CKD. Ці трикутники прямокутні: кути CKD і BHD прямі. Кути CDK і BDH рівні за гіпотенузою та гострим кутом. Якщо трикутники рівні, то рівні і їх відповідні сторони: ВН=СК. Отже, вершини В і С рівновіддалені від медіани AD.
Властивість 3.
Медіани трикутника перетинаються в одній точці та діляться нею у відношенні 2:1 починаючи від вершини.
 Доведення
Доведення
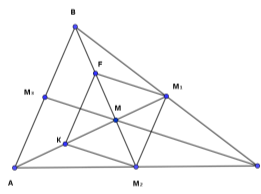
Нехай АВС – даний трикутник, АМ1 і ВМ2 – його медіани, що перетинаються в точці М. Сполучимо послідовно точки М1 і М2 та середини відрізків АМ і ВМ. Оскільки М1М2 – середня лінія трикутника АВС, то М1М2║АВ, М1М2 = ![]() АВ. В трикутнику АВМ: КF – середня лінія, КF║АВ, КF =
АВ. В трикутнику АВМ: КF – середня лінія, КF║АВ, КF =![]() АВ. Звідси КF = М1М2 і КF║ М1М2, отже, чотирикутник КFМ1М2 – паралелограм. За властивістю діагоналей паралелограма FМ = ММ2 і КМ = ММ1. Тоді ВF = FМ = ММ2 і АК = КМ = ММ1. Тобто
АВ. Звідси КF = М1М2 і КF║ М1М2, отже, чотирикутник КFМ1М2 – паралелограм. За властивістю діагоналей паралелограма FМ = ММ2 і КМ = ММ1. Тоді ВF = FМ = ММ2 і АК = КМ = ММ1. Тобто![]() , що й треба було довести. Провівши третю медіану СМ3, аналогічно можна показати , що точка перетину медіан також поділяє її у співвідношенні 2 :1. Що і потрібно було довести.
, що й треба було довести. Провівши третю медіану СМ3, аналогічно можна показати , що точка перетину медіан також поділяє її у співвідношенні 2 :1. Що і потрібно було довести.
Той факт, що три медіани перетинаються в одній точці, був доведений ще Архімедом.
Властивість 4.
Медіана трикутника менша півсуми сторін, проведених з тієї самої вершини, що й медіана.
Доведення
 Нехай АВС – даний трикутник, АМ – медіана. Відкладемо на продовженні медіани АМ відрізок МК = АМ. Тоді в чотирикутнику АВКС діагоналі перетинаються і в точці перетину діляться навпіл. Звідси АВКС – паралелограм. Застосуємо нерівність трикутника до ∆АВК: 2АМ = АК < АВ + ВК = АВ + АС. Звідси випливає, що АМ <
Нехай АВС – даний трикутник, АМ – медіана. Відкладемо на продовженні медіани АМ відрізок МК = АМ. Тоді в чотирикутнику АВКС діагоналі перетинаються і в точці перетину діляться навпіл. Звідси АВКС – паралелограм. Застосуємо нерівність трикутника до ∆АВК: 2АМ = АК < АВ + ВК = АВ + АС. Звідси випливає, що АМ < ![]() (АВ + АС). Що і потрібно було довести.
(АВ + АС). Що і потрібно було довести.
Властивість 5.
Якщо а, b, с – сторони трикутника, то довжини медіан цього трикутника обчислюють за формулами:
та = ![]() ;
;
тb = ![]() ;
;
тс = ![]()
(та, тb, тс —медіани, проведені до сторін а, b, с відповідно).
Доведення
 Нехай у трикутнику ABC ВС = а, АС = b, АВ = с, АМ — медіана, АМ = та. Продовжимо медіану АМ так, що AМ = МD. Позначимо ВC = d1, АD = d2. Оскільки діагоналі чотирикутника ABDC перетинаються і в точці перетину діляться навпіл, то за ознакою паралелограма цей чотирикутник — паралелограм , у якому діагональ AD = 2ma.
Нехай у трикутнику ABC ВС = а, АС = b, АВ = с, АМ — медіана, АМ = та. Продовжимо медіану АМ так, що AМ = МD. Позначимо ВC = d1, АD = d2. Оскільки діагоналі чотирикутника ABDC перетинаються і в точці перетину діляться навпіл, то за ознакою паралелограма цей чотирикутник — паралелограм , у якому діагональ AD = 2ma.
За теоремою косинусів із трикутника ABС маємо:
BС2 = AB2 + AС2 – 2 ∙ AB ∙ AС ∙ cosA,
![]() = с2 + b2 – 2сbcosA. (1)
= с2 + b2 – 2сbcosA. (1)
За теоремою косинусів із трикутника ABD маємо:
АD 2 = АВ2 + ВD2 – 2 ∙ AB ∙ BD ∙ cosB, або
АD2 = АВ2 + ВD2 – 2 ∙ АВ ∙ ВD ∙ cos(180°- A),
АD2 = АВ2 + ВD2 + 2 ∙ АВ ∙ ВD ∙ cos A,
![]() = с2+ b2 + 2abcosA. (2)
= с2+ b2 + 2abcosA. (2)
Додавши рівності (1) і (2) почленно, одержимо: ![]() +
+ ![]() = 2(с2 + b2)
= 2(с2 + b2)
Звідси ![]() + (2та)2 = 2(b2 + с2). Із останньої рівності знаходимо, що та:
+ (2та)2 = 2(b2 + с2). Із останньої рівності знаходимо, що та:
та = ![]() .
.
Міркуючи аналогічно, знаходимо медіани тb і тс:
тb = ![]() ; mс =
; mс = ![]() . Що і потрібно було довести.
. Що і потрібно було довести.
Властивість 6.
Медіана трикутника ділить його на два рівних за площею (рівновеликих) трикутники.
Доведення
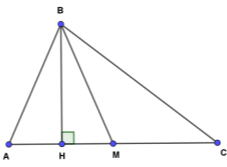 Нехай ВМ – медіана трикутника АВС. Розглянемо ∆АВМ. Проведемо в ньому висоту ВН.
Нехай ВМ – медіана трикутника АВС. Розглянемо ∆АВМ. Проведемо в ньому висоту ВН.
S∆АВМ = ![]() АМ·ВН =
АМ·ВН = ![]() ·
·![]() АС·ВН =
АС·ВН =
= ![]() АС·ВН. Розглянемо ∆СВМ: ВН – його висота, МС =
АС·ВН. Розглянемо ∆СВМ: ВН – його висота, МС = ![]() АС.
АС.
Звідси S∆СВМ = ![]() АС·ВН. Отже, S∆АВМ = S∆СВМ. Що і потрібно було довести.
АС·ВН. Отже, S∆АВМ = S∆СВМ. Що і потрібно було довести.
Властивість 7.
Якщо з’єднати точку перетину медіан трикутника з вершинами, то трикутник розбивається на три рівновеликі трикутники, тобто у цих трикутників рівні площі.![]()
Доведення
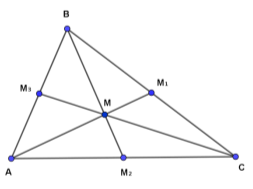 Нехай М – точка перетину медіан трикутника АВС, M1 – середина сторони ВC. Тоді MМ1 – медіана трикутника ВМC і трикутники ВМM1 і СМM1 рівновеликі (дивитися властивість 6). Оскільки АM1 – медіана трикутника ABC, то рівновеликими також є трикутники ABM1 і АСM1. Звідси, площі трикутників ABМ і АСМ рівні. Аналогічно доводимо , что рівні площі трикутників ABМ і CВМ . Отже, SABМ = SАСМ = SСВМ . Що і потрібно було довести.
Нехай М – точка перетину медіан трикутника АВС, M1 – середина сторони ВC. Тоді MМ1 – медіана трикутника ВМC і трикутники ВМM1 і СМM1 рівновеликі (дивитися властивість 6). Оскільки АM1 – медіана трикутника ABC, то рівновеликими також є трикутники ABM1 і АСM1. Звідси, площі трикутників ABМ і АСМ рівні. Аналогічно доводимо , что рівні площі трикутників ABМ і CВМ . Отже, SABМ = SАСМ = SСВМ . Що і потрібно було довести.
Властивість 8.
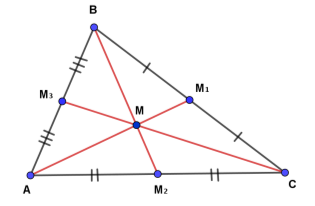
Три медіани трикутника ділять його на 6 рівних за площею (рівновеликих) трикутники.
Доведення
Скориставшись властивостями 6 і 7 отримаємо: SABМ = SАСМ = SСВМ і ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() . Звідси
. Звідси ![]() =
=![]() =
= ![]() =
=![]() =
= ![]() =
=![]() =
= ![]() . Що і потрібно було довести.
. Що і потрібно було довести.
Властивість 9.
Точка перетину медіан при паралельному проектуванні трикутника на площину переходить в точку перетину медіан спроектованого трикутника. (Такою властивістю не володіють точки перетину бісектрис та висот).
Доведення
При паралельному проектуванні відношення відрізків однієї прямої зберігається. Оскільки точка перетину медіан (центроїд) поділяє медіану у відношенні 2:1, починаючи від вершини трикутника, то центроїд при паралельному проектуванні трикутника на площину переходить у центроїд спроектованого трикутника. Що і потрібно було довести.
Властивість 10.
Довжини медіан і довжини сторін трикутника пов’язані формулою
![]() +
+ ![]() +
+ ![]() =
= ![]() (a2 + b2 + c2)
(a2 + b2 + c2)
 Доведення
Доведення
За формулою ![]() =
=![]() :
:
![]() +
+ ![]() +
+ ![]() =
= ![]() +
+![]() +
+![]() +
+![]() -
-![]() +
+![]() +
+![]() +
+![]() -
-![]() =
= ![]() (a2 + b2 + c2).
(a2 + b2 + c2).
Що і потрібно було довести.
Властивість 11.
Якщо дві медіани трикутника перпендикулярні, то сума квадратів сторін, до яких вони проведені, в 5 разів більша квадрату третьої сторони.
Доведення
 Нехай медіана ВМ2 перпендикулярна до медіани СМ3. За властивістю медіан трикутника ВМ: ММ2 = 2:1, тоді ВМ =
Нехай медіана ВМ2 перпендикулярна до медіани СМ3. За властивістю медіан трикутника ВМ: ММ2 = 2:1, тоді ВМ = ![]() ВМ2 , а СМ =
ВМ2 , а СМ =![]() СМ3. Тоді
СМ3. Тоді ![]() (
(![]() +
+![]() ) = а2 або
) = а2 або ![]()
![]() = а2,
= а2,
або b2 + c2 = 5a2. Що і потрібно було довести.
Властивість 12.
Сума трьох векторів, що виходять з точки перетину медіан до вершин трикутника, рівна нулю.
Доведення
 Нехай М – точка перетину медіан трикутника АВС. Доведемо, що
Нехай М – точка перетину медіан трикутника АВС. Доведемо, що ![]() . Медіани АМ1, ВМ2, СМ3 трикутника АВС точкою перетину М діляться у відношенні 1:2. Відкладемо на промені АМ вектор
. Медіани АМ1, ВМ2, СМ3 трикутника АВС точкою перетину М діляться у відношенні 1:2. Відкладемо на промені АМ вектор ![]() . Вектори
. Вектори ![]() і
і ![]() мають рівні довжини і протилежно напрямлені, тому
мають рівні довжини і протилежно напрямлені, тому ![]() +
+ ![]() =
=![]() . Чотирикутник ВМСК – паралелограм, тому за правилом паралелограма
. Чотирикутник ВМСК – паралелограм, тому за правилом паралелограма ![]() . Отже,
. Отже, ![]() . Що і потрібно було довести.
. Що і потрібно було довести.
- Медіана у рівнобедреному трикутнику
Властивість 1.
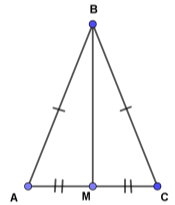
Медіана рівнобедреного трикутника, проведена до основи, є бісектрисою і висотою .
 Доведення
Доведення
Нехай АВС – даний рівнобедрений трикутник з основою АС. ВМ – медіана, проведена до основи. Розглянемо ∆АВМ і ∆CВМ.
В них:
1) АВ = СВ (як бічні сторони рівнобедреного трикутника),
2) АМ = СМ (ВМ – медіана, проведена до АС),
3) ВМ – спільна.
Отже, ∆АВМ = ∆CВМ за трьома сторонами. З рівності трикутників маємо:
![]() АВМ =
АВМ = ![]() СВМ,
СВМ, ![]() АМВ =
АМВ = ![]() СМВ. Оскільки
СМВ. Оскільки ![]() АВМ =
АВМ = ![]() СВМ, то
СВМ, то
ВМ – бісектриса кута В. Оскільки ![]() АМВ =
АМВ = ![]() СМВ і вони суміжні, тому
СМВ і вони суміжні, тому
![]() АМВ =
АМВ = ![]() СМВ = 90º, тобто ВМ – висота, проведена до АС.
СМВ = 90º, тобто ВМ – висота, проведена до АС.
Отже, медіана рівнобедреного трикутника, проведена до основи, є бісектрисою і висотою. Що і потрібно було довести.
Властивість 2.
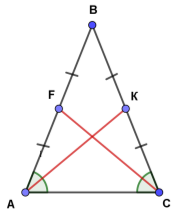
В рівнобедреному трикутнику медіани, проведені до бічних сторін, рівні.
 Доведення
Доведення
Нехай АВС – даний рівнобедрений трикутник з основою АС. AK, CF – медіани, проведені до бічних сторін. Оскільки бічні сторони АВ і СВ рівнобедреного трикутника рівні, то рівними будуть і їх половини ![]() АВ =
АВ = ![]() СВ, тобто AF = СК.
СВ, тобто AF = СК.
За властивістю кутів при основі рівнобедреного трикутника ![]() А =
А = ![]() С. ∆АСF = ∆CAK за двома сторонами і кутом між ними (AF = СК,
С. ∆АСF = ∆CAK за двома сторонами і кутом між ними (AF = СК, ![]() А =
А =![]() С, АС = СА). З рівності трикутників випливає рівність медіан AK = СF . Що і потрібно було довести.
С, АС = СА). З рівності трикутників випливає рівність медіан AK = СF . Що і потрібно було довести.
Властивість 3.
В рівносторонньому трикутнику медіани рівні.
Доведення
З попередньої властивості маємо, що медіани трикутника, проведені до рівних сторін, рівні. Оскільки в рівносторонньому трикутнику всі сторони рівні, то медіани, проведені до цих сторін, також рівні. Що і потрібно було довести.
1.3. Медіана у прямокутному трикутнику
Властивість 1.
Медіана, проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи.
( доведення дивитися в розділі ІІ )
Властивість 2.
У прямокутному трикутнику медіана, що проведена з вершини прямого кута розділяє трикутник його на два необов’язково рівних рівнобедрених трикутники.
Доведення (доведення очевидне з попередньої властивості)
Властивість 3.
Якщо гострі кути прямокутного трикутника відносяться, як 1:2, то медіана, проведена до гіпотенузи, дорівнює одному з катетів цього трикутника.
 Доведення
Доведення
Нехай АВС (![]() С = 90º) – даний трикутник, АМ – медіана,
С = 90º) – даний трикутник, АМ – медіана, ![]() А:
А:![]() В = 1:2. Позначимо
В = 1:2. Позначимо ![]() А = х,
А = х, ![]() В = 2х. Сума гострих кутів прямокутного трикутника дорівнює 90º. Тоді х + 2х = 90, 3х = 90, х =30. Звідси
В = 2х. Сума гострих кутів прямокутного трикутника дорівнює 90º. Тоді х + 2х = 90, 3х = 90, х =30. Звідси ![]() А = 30 º,
А = 30 º, ![]() В = 60º . З попередньої властивості маємо: СМ = МВ. Розглянемо ∆ СМВ, в ньому СМ = МВ, тобто він рівнобедрений.
В = 60º . З попередньої властивості маємо: СМ = МВ. Розглянемо ∆ СМВ, в ньому СМ = МВ, тобто він рівнобедрений. ![]() МВС =
МВС = ![]() МСВ як кути при основі рівнобедреного трикутника.
МСВ як кути при основі рівнобедреного трикутника.
Звідси ![]() МСВ =
МСВ = ![]() МВС = 60º,
МВС = 60º, ![]() СМВ = 180º -
СМВ = 180º - ![]() МСВ -
МСВ - ![]() МВС = 60º.
МВС = 60º.
Отже, ∆СМВ – рівносторонній. Звідси СМ = СВ. Що і потрібно було довести.
РОЗДІЛ ІІ. Властивість одна – способи доведення різні
Властивість
Медіана, проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи.
Доведення
Спосіб 1
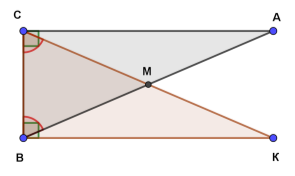 З точки В проведемо перпендикуляр ВК до сторони ВС так, що ВК = СА. Тоді ∆АВС і ∆КСВ – прямокутні, до того ж ВС – спільний катет цих трикутників і АС = КВ (за побудовою). Тому ∆АВС = ∆КСВ (за двома катетами), тоді
З точки В проведемо перпендикуляр ВК до сторони ВС так, що ВК = СА. Тоді ∆АВС і ∆КСВ – прямокутні, до того ж ВС – спільний катет цих трикутників і АС = КВ (за побудовою). Тому ∆АВС = ∆КСВ (за двома катетами), тоді ![]() АВС =
АВС = ![]() КСВ. Отже, ∆МВС – рівнобедрений і
КСВ. Отже, ∆МВС – рівнобедрений і
ВМ = СМ. Аналогічно можна довести, що СМ = АМ.
Таким чином, ВМ = СМ = АМ. Тому СМ – медіана і СМ = ![]() , що і треба було довести.
, що і треба було довести.
Спосіб 2
 Розглянемо ∆АВС(
Розглянемо ∆АВС(![]() С = 90º). Із вершини прямого кута С проведемо до гіпотенузи АВ відрізок СМ так, що СМ = МА. ∆АМС – рівнобедрений з основою АС (за означенням рівнобедреного трикутника). За властивістю кутів при основі рівнобедреного трикутника
С = 90º). Із вершини прямого кута С проведемо до гіпотенузи АВ відрізок СМ так, що СМ = МА. ∆АМС – рівнобедрений з основою АС (за означенням рівнобедреного трикутника). За властивістю кутів при основі рівнобедреного трикутника ![]() МАD =
МАD =![]() МСD. Нехай
МСD. Нехай ![]() МАD =
МАD =![]() МСD =
МСD =![]() . Оскільки сума гострих кутів прямокутного трикутника дорівнює 90º, то в трикутнику АВС
. Оскільки сума гострих кутів прямокутного трикутника дорівнює 90º, то в трикутнику АВС ![]() В=90º-
В=90º- ![]() . Оскільки
. Оскільки ![]() ВСА = 90º (за умовою), то
ВСА = 90º (за умовою), то ![]() ВСМ = 90º -
ВСМ = 90º - ![]() МСА = 90º -
МСА = 90º -![]() .
.
Розглянемо ∆ВМС, в ньому ![]() ВСМ = 90º -
ВСМ = 90º -![]() ,
, ![]() В = 90º -
В = 90º -![]() . Звідси:
. Звідси: ![]() ВСМ =
ВСМ = ![]() В. Отже, ∆ВМС – рівнобедрений з основою ВС (за ознакою рівнобедреного трикутника). Звідси: ВМ = СМ.
В. Отже, ∆ВМС – рівнобедрений з основою ВС (за ознакою рівнобедреного трикутника). Звідси: ВМ = СМ.
Так як СМ = МА (за побудовою) і ВМ = СМ (за доведеним), то
СМ = МА = ВМ. Таким чином, точка М – середина гіпотенузи АВ, відрізок СМ сполучає вершину трикутника із серединою протилежної сторони, отже, СМ – медіана, проведена до гіпотенузи, і вона дорівнює половині гіпотенузи:
СМ = ![]() АВ. Що і треба було довести.
АВ. Що і треба було довести.
Спосіб 3
 Проведемо МК
Проведемо МК![]() СВ. Оскільки АС
СВ. Оскільки АС![]() СВ і МК
СВ і МК![]() СВ, то АС║МК. Проведемо МD
СВ, то АС║МК. Проведемо МD![]() АС. Оскільки СВ
АС. Оскільки СВ![]() АС і МD
АС і МD![]() АС, то СВ║МD.
АС, то СВ║МD.
∆АDМ =∆МКВ за гіпотенузою і гострим кутом, бо АМ = МВ (СМ – медіана, проведена до АВ ) і ![]() DАМ =
DАМ = ![]() КМВ як відповідні кути при АС║МК та січній АВ. З рівності трикутників отримаємо:
КМВ як відповідні кути при АС║МК та січній АВ. З рівності трикутників отримаємо:
АD = МК, DМ = КВ.
∆МКС = ∆СDМ за гіпотенузою і гострим кутом, бо СМ – спільна і ![]() КСМ =
КСМ = ![]() DМС як внутрішні різносторонні кути при СВ║МD та січній СМ. З рівності трикутників отримаємо: МК = DС, КС = МD.
DМС як внутрішні різносторонні кути при СВ║МD та січній СМ. З рівності трикутників отримаємо: МК = DС, КС = МD.
∆АDМ = ∆МКВ = ∆МКС = ∆СDМ за двома катетами. Звідси АМ = МВ = МС. СМ = ![]() АВ. Що і потрібно було довести.
АВ. Що і потрібно було довести.
Спосіб 4
 Продовжимо відрізок СМ. Відкладемо на промені СМ відрізок МD = СМ. Розглянемо чотирикутник САDВ. В нього діагоналі перетинаються і в точці перетину діляться навпіл: АМ = ВМ (СМ – медіана, проведена до АВ) і СМ = МD (за побудовою), тому САDВ – паралелограм (за ознакою паралелограма). Оскільки
Продовжимо відрізок СМ. Відкладемо на промені СМ відрізок МD = СМ. Розглянемо чотирикутник САDВ. В нього діагоналі перетинаються і в точці перетину діляться навпіл: АМ = ВМ (СМ – медіана, проведена до АВ) і СМ = МD (за побудовою), тому САDВ – паралелограм (за ознакою паралелограма). Оскільки ![]() АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ =
АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ = ![]() АВ, що і треба було довести.
АВ, що і треба було довести.
Спосіб 5
 Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Звідси: МD – медіана ∆АМС. Оскільки МD║ВС і ВС
Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Звідси: МD – медіана ∆АМС. Оскільки МD║ВС і ВС![]() АС, то МD
АС, то МD![]() АС. Звідси: МD – висота ∆АМС. Медіана МD ∆АМС є і висотою. Отже, ∆АМС – рівнобедрений, в ньому АМ=МС. Звідси: МС=АМ=МВ.
АС. Звідси: МD – висота ∆АМС. Медіана МD ∆АМС є і висотою. Отже, ∆АМС – рівнобедрений, в ньому АМ=МС. Звідси: МС=АМ=МВ.
Отже, МС = ![]() АВ.
АВ.
Спосіб 6
 Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Оскільки МD║ВС і ВС
Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Оскільки МD║ВС і ВС![]() АС, то МD
АС, то МD![]() АС. Звідси ∆АDМ і ∆СDМ – прямокутні. Розглянемо ∆АDМ(
АС. Звідси ∆АDМ і ∆СDМ – прямокутні. Розглянемо ∆АDМ(![]() D=90º) і ∆СDМ(
D=90º) і ∆СDМ(![]() D=90º), в них:
D=90º), в них:
- МD – спільна,
- АD=DС.
Отже, ∆АDМ = ∆СDМ за двома катетами. Звідси:
АМ=СМ. Отже, МС = ![]() АВ.
АВ.
Спосіб 7
 Проведемо ВD║СА. Продовжимо СМ до перетину з ВD. Розглянемо ∆САМ і ∆DВМ. В них:
Проведемо ВD║СА. Продовжимо СМ до перетину з ВD. Розглянемо ∆САМ і ∆DВМ. В них:
1) АМ = ВМ, бо М – середина АВ,
2) ![]() АМС =
АМС =![]() ВМD як вертикальні,
ВМD як вертикальні,
3) ![]() САМ =
САМ =![]() DВМ як внутрішні різносторонні кути при СА║ ВD і січній АВ. Таким чином, ∆САМ = ∆DВМ за стороною і двома прилеглими кутами. Звідси СА = DВ. САDВ – паралелограм, бо СА║ВD і СА = ВD.
DВМ як внутрішні різносторонні кути при СА║ ВD і січній АВ. Таким чином, ∆САМ = ∆DВМ за стороною і двома прилеглими кутами. Звідси СА = DВ. САDВ – паралелограм, бо СА║ВD і СА = ВD.
Оскільки ![]() АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ =
АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ = ![]() АВ, що і треба було довести.
АВ, що і треба було довести.
Спосіб 8
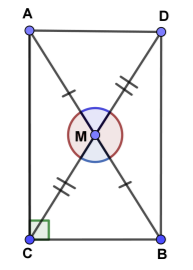
Продовжимо відрізок СМ. Відкладемо на промені СМ відрізок МD = СМ. Розглянемо ∆СМА і ∆DМВ. В них:
1) АМ = ВМ, бо М – середина АВ,
2) СМ = DМ за побудовою,
3) ![]() АМС =
АМС =![]() ВМD як вертикальні.
ВМD як вертикальні.
Таким чином, ∆СМА = ∆DМВ за двома сторонами і кутом між ними. Звідси СА = DВ. Аналогічно ∆АМD = ∆ВМС. Звідси АD = ВС. Чотирикутник САDВ – паралелограм, бо СА = DВ і АD = ВС. Оскільки ![]() АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ =
АСВ=90º, то САDВ – прямокутник. СD = ВА як діагоналі прямокутника і СМ = DМ = АМ = МВ. Отже, СМ = ![]() АВ, що і треба було довести.
АВ, що і треба було довести.
Спосіб 9
 Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Звідси: DМ – середня лінія ∆АВС. За властивістю середньої лінії: DМ=
Проведемо МD║ВС. Оскільки АМ=МВ і МD║ВС, то за теоремою Фалеса АD=DС. Звідси: DМ – середня лінія ∆АВС. За властивістю середньої лінії: DМ=![]() СВ. Проведемо МК║АС. За теоремою Фалеса ВК=КС. Звідси: МК – середня лінія ∆АВС і МК=
СВ. Проведемо МК║АС. За теоремою Фалеса ВК=КС. Звідси: МК – середня лінія ∆АВС і МК=![]() АС.
АС.
СDМВ – прямокутник, оскільки DМ║СК, МК║DС і![]() С=90º. Діагональ СМ прямокутника шукаємо за теоремою Піфагора:
С=90º. Діагональ СМ прямокутника шукаємо за теоремою Піфагора:
СМ2= СК2+МК2=(![]() СВ)2+(
СВ)2+(![]() АС)2;
АС)2;
СМ =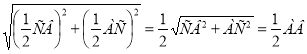 . Отже, СМ =
. Отже, СМ = ![]() АВ.
АВ.
Що і потрібно було довести.
Спосіб 10
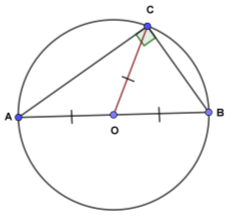 Розглянемо коло з діаметром АВ. О – центр цього кола. Візьмемо довільну точку С на колі.
Розглянемо коло з діаметром АВ. О – центр цього кола. Візьмемо довільну точку С на колі. ![]() АСВ – вписаний у коло кут, який спирається на діаметр. За властивістю вписаних кутів:
АСВ – вписаний у коло кут, який спирається на діаметр. За властивістю вписаних кутів:
![]() АСВ =
АСВ = ![]()
![]() АОВ =
АОВ = ![]() ·180º = 90º.
·180º = 90º.
Отже, ∆АВС – прямокутний з гіпотенузою АВ. СО – медіана ∆АВС, бо АО = ВО як радіуси кола. СО також є радіусом цього кола. Звідси АО = ВО = СО, тобто СО = ![]() АВ, що і треба було довести.
АВ, що і треба було довести.
![]()
Спосіб 11

Введемо систему координат. Розмістимо прямокутний трикутник АВС(![]() С=90º) так, щоб вершина прямого кута співпадала з початком координат, а катети лежали на осях. Тоді: С(0;0), А(а;0); В(0;b). Якщо М(х0;у0) – середина АВ, то СМ – медіана ∆АВС, проведена до гіпотенузи. Знайдемо координати точки М:
С=90º) так, щоб вершина прямого кута співпадала з початком координат, а катети лежали на осях. Тоді: С(0;0), А(а;0); В(0;b). Якщо М(х0;у0) – середина АВ, то СМ – медіана ∆АВС, проведена до гіпотенузи. Знайдемо координати точки М: ![]() ,
, ![]() . Тобто М
. Тобто М![]() . Знайдемо довжини відрізків АМ, ВМ і СМ: АМ =
. Знайдемо довжини відрізків АМ, ВМ і СМ: АМ = 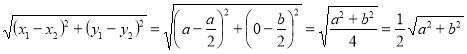 ,
,
ВМ = 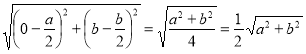 ,
,
СМ = 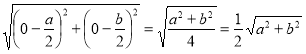 .
.
Звідси АМ = ВМ = СМ. Отже, СМ = ![]() АВ. Що і потрібно було довести.
АВ. Що і потрібно було довести.
Спосіб 12
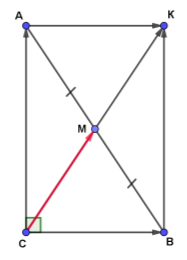 За правилом паралелограма виразимо
За правилом паралелограма виразимо ![]() через
через ![]() і
і ![]() . Маємо:
. Маємо: ![]() . Оскільки
. Оскільки ![]() , то
, то 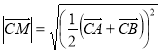 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Отже, СМ = ![]() АВ. Що і потрібно було довести.
АВ. Що і потрібно було довести.
Спосіб 13
Позначимо АВ = с, АС = b, ВС = а. Використаємо формулу:
тс = ![]() . Оскільки в ∆АВС за теоремою Піфагора: с2 = а2 + b2, то тс =
. Оскільки в ∆АВС за теоремою Піфагора: с2 = а2 + b2, то тс = ![]() =
= ![]() =
= ![]() =
= ![]() . Отже, тс =
. Отже, тс = ![]() .
.
Cпосіб 14

Застосуємо до ∆АВС(![]() АСВ=90º) симетрію відносно точки М – середини сторони АВ. ∆АВС перейде у ∆ВАD. Оскільки АМ = ВМ (за умовою), СМ = DМ (точки С і D симетричні відносно точки М) і
АСВ=90º) симетрію відносно точки М – середини сторони АВ. ∆АВС перейде у ∆ВАD. Оскільки АМ = ВМ (за умовою), СМ = DМ (точки С і D симетричні відносно точки М) і ![]() АСВ=90º, то чотирикутник САDВ є прямокутником. Діагоналі прямокутника рівні і точкою перетину діляться навпіл, тобто СМ = DМ = АМ = МВ.
АСВ=90º, то чотирикутник САDВ є прямокутником. Діагоналі прямокутника рівні і точкою перетину діляться навпіл, тобто СМ = DМ = АМ = МВ.
Отже, СМ = ![]() АВ. Що і треба було довести.
АВ. Що і треба було довести.
РОЗДІЛ ІІІ. Метод подвоєння медіани
Для розв’язування деяких геометричних задач потрібно проводити додаткові побудови, тобто добудовувати відрізки й кути, не згадані в умові задачі. Це робиться для отримання допоміжних фігур, розгляд яких дозволяє знайти або довести необхідне. Існують певні види додаткових побудов, що їх застосовують найчастіше. Один із них ми розглянемо в наступній задачі.
Задача
Якщо в трикутнику медіана й бісектриса, проведені з однієї вершини, збігаються, то такий трикутник рівнобедрений. Доведіть.
Розв’язання
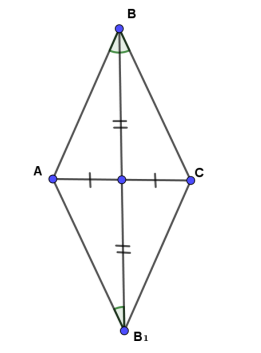 Нехай BD – медіана й бісектриса даного трикутника ABC. Доведемо, що трикутник ABC є рівнобедреним.
Нехай BD – медіана й бісектриса даного трикутника ABC. Доведемо, що трикутник ABC є рівнобедреним.
На промені BD від точки D відкладено відрізок DB1, що дорівнює BD (тобто подвоїмо медіану BD).
Розглянемо трикутники BDC і B1DA. У них AD=CD за означенням медіани, BD=B1D за побудовою, ![]() BDC=
BDC=![]() B1DA, як вертикальні. Таким чином, ∆BDC=∆B1DA за першою ознакою рівності трикутників. Звідси випливає, що
B1DA, як вертикальні. Таким чином, ∆BDC=∆B1DA за першою ознакою рівності трикутників. Звідси випливає, що ![]() 3=
3=![]() 2 і AB1=CB. Розглянемо тепер трикутник BAB1. З огляду на те, що BD – бісектриса кута ABC, маємо
2 і AB1=CB. Розглянемо тепер трикутник BAB1. З огляду на те, що BD – бісектриса кута ABC, маємо ![]() 1=
1=![]() 2, тоді
2, тоді ![]() 1=
1=![]() 3. За ознакою рівнобедреного трикутника трикутник BAB1 є рівнобедреним з основою BB1. Звідси AB1=AB, а оскільки з доведеного AB1=CB, то AB=CB. Таким чином, трикутник ABC рівнобедрений, що й треба було довести.
3. За ознакою рівнобедреного трикутника трикутник BAB1 є рівнобедреним з основою BB1. Звідси AB1=AB, а оскільки з доведеного AB1=CB, то AB=CB. Таким чином, трикутник ABC рівнобедрений, що й треба було довести.
Проаналізуємо розв’язання цієї задачі. Відображення всіх даних умови на рисунку не виявило набору елементів, які дозволяють відразу розпочати доведення. Це зумовило необхідність додаткової побудови, завдяки якій утворився допоміжний трикутник B1DA. Довівши його рівність із трикутником DBC, ми дістали додаткові рівності відрізків та кутів і розв’язали задачу.
Додаткова побудова полягала в подвоєнні відрізка BD. Така побудова використовується найчастіше саме для медіан трикутників, тому метод доведення, що ґрунтується на ній, називають методом подвоєння медіани.
Задача 1.
Дві сторони трикутника дорівнюють 7 см і 11 см, а медіана, проведена до третьої сторони, дорівнює 6 см. Знайдіть третю сторону.
Розв'язання
 Нехай у трикутнику ABC АВ = 7 см, ВС = 11 см, BD — медіана (AD = DC), BD = 6 см.
Нехай у трикутнику ABC АВ = 7 см, ВС = 11 см, BD — медіана (AD = DC), BD = 6 см.
Продовжимо медіану BD і відкладемо на продовженні відрізок DF так, що DF = BD. Чотирикутник ABCF — це паралелограм (оскільки діагоналі АС і BF точкою перетину діляться навпіл), тоді АС² + BF² = 2 ∙ (AB² + BC²).
Звідси АС² + 12² = 2 ∙ (7² + 11²), тоді АС² + 144 = 340;
АС2 =196;
АС² =![]() = 14 (см).
= 14 (см).
Відповідь. 14 см.
Задача 2.
У∆ АВС (b>c) проведена медіана ma .
Який з кутів більший ![]() 1 чи
1 чи ![]() 2?
2? ![]() 3 чи
3 чи ![]() 4?
4?
Розв'язання
Продовживши медіану ma, отримаємо паралелограм ABDC, в якому CD = c i ![]() ADC =
ADC = ![]() 2 (як внутрінші різносторонні).
2 (як внутрінші різносторонні).
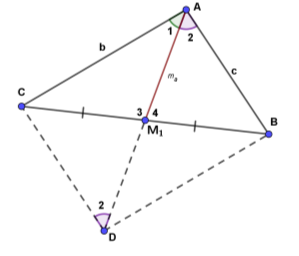 У трикутнику АСD проти сторони b лежить
У трикутнику АСD проти сторони b лежить ![]() 2, а проти с –
2, а проти с – ![]() 1.
1.
Оскільки b > c, то ![]() 2 >
2 >![]() 1.
1.
Крім того, ![]() 3=
3=![]() 2 +
2 + ![]() В (зовнішній кут для
В (зовнішній кут для ![]() АСМ1 ).
АСМ1 ).
Тоді очевидно, що ![]() 3 >
3 >![]() 4.
4.
Задача 3.
Довести, що в будь-якому трикутнику сума медіан ma+mb+mc більша ![]() периметра, але менша всього периметра.
периметра, але менша всього периметра.
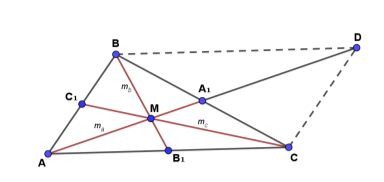 Розв'язання
Розв'язання
Нехай для трикутника АВС точка D - симетрична до А відносно середини А1 сторони АС .
Тоді 2та=АD<АВ+ВD = =АВ+АС=b+с.
Аналогічно доводимо, що 2тb < а+с, 2тс<b+а.
Додавши ці нерівності, одержимо ma+mb+mc < а+b+с.
В іншу сторону, якщо М - точка перетину медіан, то
АМ+ВМ > АВ, ВМ+СМ >ВС, АМ+СМ >АС.
Додаючи ці нерівності і враховуючи, що
![]() , ,
, , ![]() , C
, C![]() ,
,
одержимо ![]() (та + тb + тс) > а + b + с.
(та + тb + тс) > а + b + с.
Звідси і випливає потрібна нерівність.
РОЗДІЛ ІV. Медіана в олімпіадних задачах
Властивості медіан трикутника часто використовуються під час розв’язування олімпіад них задач.
Задача 1.
Висоти АА1, ВВ1, СС1 гострокутного трикутника АВС перетинаються в точці Н. Точки М і N – середини відрізків ВС і АН відповідно. Доведіть, що МN – серединний перпендикуляр відрізка В1С1.
Доведення
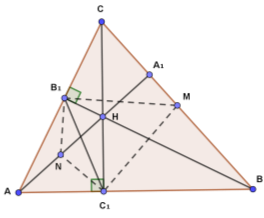 Розглянемо прямокутні трикутники ВВ1С і СС1В. В1М і С1М – медіани цих трикутників відповідно, проведені із вершин прямих кутів. За властивістю медіани прямокутника, проведеної із вершини прямого кута до гіпотенузи В1М = 0,5СВ = С1М, тобто точка М рівновіддалена від кінців відрізка В1С1. Аналогічно, розглянувши прямокутні трикутники В1АН і С1АН, отримали В1N =0,5АН = С1N, тобто точка М рівновіддалена від кінців відрізка В1С1. Таким чином, кожна із точок N і М рівновіддалена від кінців відрізка В1С1, отже, МN – серединний перпендикуляр цього відрізка. Що і потрібно було довести.
Розглянемо прямокутні трикутники ВВ1С і СС1В. В1М і С1М – медіани цих трикутників відповідно, проведені із вершин прямих кутів. За властивістю медіани прямокутника, проведеної із вершини прямого кута до гіпотенузи В1М = 0,5СВ = С1М, тобто точка М рівновіддалена від кінців відрізка В1С1. Аналогічно, розглянувши прямокутні трикутники В1АН і С1АН, отримали В1N =0,5АН = С1N, тобто точка М рівновіддалена від кінців відрізка В1С1. Таким чином, кожна із точок N і М рівновіддалена від кінців відрізка В1С1, отже, МN – серединний перпендикуляр цього відрізка. Що і потрібно було довести.
Задача 2.
В трикутнику АВС ![]() АВС = 60º, точка М – середина сторони АС, а L – точка на стороні ВС така, що АL – бісектриса
АВС = 60º, точка М – середина сторони АС, а L – точка на стороні ВС така, що АL – бісектриса ![]() ВАС. Центр кола, описаного навколо трикутника АВС, лежить на відрізку МL. Знайти величину двох інших кутів трикутника АВС.
ВАС. Центр кола, описаного навколо трикутника АВС, лежить на відрізку МL. Знайти величину двох інших кутів трикутника АВС.
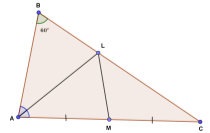 Розв’язання
Розв’язання
Оскільки центр описаного кола – це точка перетину серединних перпендикулярів до сторін трикутника, то МL – серединний перпендикуляр до відрізка АС. Тому – LМ висота і медіана трикутника АLС, звідси, цей трикутник рівнобедрений.
180º = ![]() АВС +
АВС +![]() ВАС +
ВАС +![]() ВСА = 60º + 3
ВСА = 60º + 3![]() ВСА.
ВСА.
Звідси ![]() ВСА = 40º і
ВСА = 40º і ![]() ВАС = 2
ВАС = 2![]() ВСА = 80º.
ВСА = 80º.
Відповідь. ![]() ВСА = 40º,
ВСА = 40º,![]() ВАС = 80º.
ВАС = 80º.
Задача 3.
Доведіть, що довжина медіани, яка виходить із вершини тупого кута трикутника, менша чверті периметра цього трикутника.
Доведення
Нехай а, b, с – сторони трикутника, ![]() - тупий кут (протилежний стороні с), т – медіана. Продовживши медіану на її довжину, одержимо паралелограм зі сторонами а, b і діагоналями с, 2т . Скористаємося теоремою косинусів і тим, що кут
- тупий кут (протилежний стороні с), т – медіана. Продовживши медіану на її довжину, одержимо паралелограм зі сторонами а, b і діагоналями с, 2т . Скористаємося теоремою косинусів і тим, що кут ![]() тупий.
тупий.
(2 т)2 = а2 + b2 - 2аb·соs(180º -![]() ) = а2 + b2 + 2аb·соs
) = а2 + b2 + 2аb·соs ![]() < а2 + b2 - 2аb·соs
< а2 + b2 - 2аb·соs ![]() = с2.
= с2.
Тому 2 т < с. За нерівністю трикутника с < а + b, 2с < а + b + с = Р. Звідси робимо висновок, що т <![]() . Що і потрібно було довести.
. Що і потрібно було довести.
Задача 4.
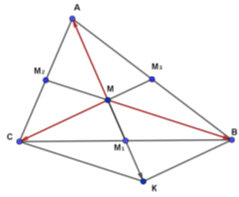
Точка А рухається по периметру трикутника KMN. Точки ![]() ,
,![]() ,
, ![]() лежать на медіанах трикутника KMN і ділять їх у відношенні 1 : 5, рахуючи від вершин. По периметру трикутника
лежать на медіанах трикутника KMN і ділять їх у відношенні 1 : 5, рахуючи від вершин. По периметру трикутника ![]() рухається точка В зі швидкістю, яка втричі більша за швидкість точки А. Скільки разів точка В обійде по периметру трикутник
рухається точка В зі швидкістю, яка втричі більша за швидкість точки А. Скільки разів точка В обійде по периметру трикутник ![]() за той час, за який точка А п’ять разів обійде по периметру трикутник KMN?
за той час, за який точка А п’ять разів обійде по периметру трикутник KMN?
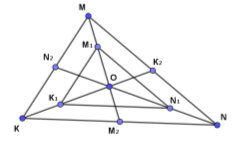 Розв’язання
Розв’язання
Як відомо, медіани трикутника перетинаються і точкою перетину діляться у
відношенні 2 : 1, рахуючи від вершини.
Тоді ![]() .
.
За умовою задачі ![]() .
.
Покажемо, що ![]() .
.
Аналогічно, ![]() ,
,
![]() .
.
![]()
![]()
![]() KON, так як
KON, так як
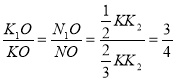 ,
, ![]() KON – спільний.
KON – спільний.
Аналогічно, ![]()
![]()
![]() KOМ і
KOМ і ![]()
![]()
![]() МON, при чому з тим самим коефіцієнтом подібності
МON, при чому з тим самим коефіцієнтом подібності ![]() .
.
Тоді, ![]() і
і ![]() .
.
Нехай швидкість руху точки А дорівнює v, тоді швидкість руху точки В дорівнює 3v. Точка А обійде периметр трикутника за час, що дорівнює ![]() , тоді п’ять разів за час
, тоді п’ять разів за час ![]() .
.
Точка В за цей час обійде периметр трикутника ![]() один раз за
один раз за ![]() .
.
Якщо кількість разів, що пройшла точка В дорівнює х, то отримаємо рівняння ![]() . Звідси х = 20.
. Звідси х = 20.
Відповідь: 20 разів.
Задача 5.
В трикутнику АВС сторона АС = 5, ВС = 3. Яка може бути довжина медіани СМ цього трикутника? ( Вкажіть усі можливі значення)
Розв’язання
 Добудуємо паралелограм АСВD.
Добудуємо паралелограм АСВD.
Тоді точка М – середина діагоналі СD, СD = 2СМ, АD = СВ.
За нерівністю трикутника маємо, що
АС + АD >СD.
Тоді, СМ = 0,5СD і СМ < 0,5(АС + АD) = 0,5(АС +ВС) = 4.
З іншого боку, АС – АD < СD. Тому для медіани СМ буде виконуватись нерівність
СМ = 0,5СD > 0,5(АС – АD) = 0,5(АС – ВС) = 1.
Таким чином, медіана СМ може набувати будь-яких значень
з інтервалу (1; 4).
При будь-якому значенні СМ з цього інтервалу буде існувати трикутник зі сторонами АС = 5, ВС = 3 і медіаною СМ.
Відповідь: довжина медіани належить проміжку (1; 4)
РОЗДІЛ V. Задачі для самостійного розв’язування
Задача 1. Якщо в трикутнику медіана і висота, проведені з однієї вершини, збігаються, то такий трикутник рівнобедрений. Доведіть.
Задача 2. Доведіть, що трикутник, у якому медіана ділить периметр навпіл, рівнобедрений.
Задача 3. Якщо медіана трикутника дорівнює половині сторони, до якої її проведено, то цей трикутник прямокутний.
Задача 4. Одна зі сторін трикутника дорівнює 10, а медіани, що проведені до двох інших сторін, дорівнюють 9 і 12. Знайти площу трикутника .
(Відповідь:72)
Задача 5. ВМ – медіана трикутника АВС. Знайдіть АВ, якщо АС = 16см,
ВС = 13см, ![]() ВМС = 120°.
ВМС = 120°.
(Відповідь: ![]() см)
см)
Задача 6. Знайдіть довжину медіани трикутника зі сторонами 12 см, 14 см і 22 см, проведену до найбільшої сторони.
(Відповідь:7см)
Задача 7. У трикутнику медіана і сторона, до якої вона проведена, дорівнюють відповідно 10 см і 30 см. Знайдіть інші сторони трикутника, якщо його периметр дорівнює 64 см.
(Відповідь:11см, 23см)
Задача 8. Дві сторони трикутника дорівнюють 6 см і 10 см, а медіана, проведена до третьої сторони, дорівнює ![]() см. Знайдіть найбільший кут трикутника.
см. Знайдіть найбільший кут трикутника.
(Відповідь:120°)
Задача 9. Знайти відстань від точки перетину медіан до центра кола, вписаного в рівнобедрений трикутник з основою 160 см і бічною стороною 100 см.
(Відповідь:![]() см)
см)
Задача 10. У трикутника зі стороною 26 см медіани, проведені до двох інших сторін, дорівнюють 15 см і 30 см. Знайдіть довжину третьої медіани.
(Відповідь:27см)
Задача 11.Знайдіть найменшу сторону трикутника, якщо дві його медіани перпендикулярні і мають довжини 3 м і 4 м.
(Відповідь:![]() м)
м)
Задача 12. В трикутнику АВС медіанаа ВМ у два рази менша за сторону АВ і утворює із нею кут 40o. Знайдіть ![]() АВС.
АВС.
(Відповідь:110°)
Задача 13. Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 3 см і ділить прямий кут у відношенні 2:1. Знайдіть менший катет.
(Відповідь:3см)
Задача 14. АА1, ВВ1, СС1 – медіани трикутника АВС. ![]() .
.
Знайдіть ![]() .
.
(Відповідь:1,5)
Задача 15. Медіани ∆АВС АА1, ВВ1 і СС1 перетинаються в точці О, ![]() ,
, ![]() см,
см, ![]() см. Знайдіть ВО.
см. Знайдіть ВО.
(Відповідь:10см)
Задача 16. Медіани трикутника дорівнюють 5, ![]() і
і ![]() . Доведіть, що трикутник прямокутний.
. Доведіть, що трикутник прямокутний.
Задача 17. Числа ![]() ,
, ![]() і
і ![]() задають довжини медіан деякого трикутника. Доведіть, що якщо виконується рівність
задають довжини медіан деякого трикутника. Доведіть, що якщо виконується рівність ![]() , то трикутник прямокутний.
, то трикутник прямокутний.
Задача 18. Сторони трикутника дорівнюють 13, 14 і 15. Знайти площі трикутників, на які разбивається даний трикутник його медіанами.
(Відповідь:14)
Задача 19. Одна сторона трикутника дорівнює а, друга – b. Знайдіть третю сторону, коли відомо, що вона дорівнює медіані, проведеній до неї.
(Відповідь: 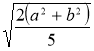 )
)
Задача 20. Дано ∆ ABC, площа якого дорівнює 2. На медіанах AK, BL і CN ∆ ABC взяті відповідно точки P, Q і R так, що AP : PK = 1, BQ : QL = 1 : 2, CR : RN = 5 : 4. Знайдіть площу ∆ PQR.
(Відповідь:![]() )
)
Задача 21. Медіани трикутника дорівнюють 3, 4 і 5. Знайдіть площу трикутника.
(Відповідь:8)
Задача 22. На двох сторонах трикутника (зовні його) побудовані квадрати. Доведіть, що відрізок, який сполучає кінці сторін квадратів, що виходять із однієї вершини трикутника, у два рази більший за медіану трикутника, яка виходить із тієї ж вершини.
Задача 23. Медіани CM і BN прямокутного трикутника АВС (![]() С= 900), перпендикулярні. Знайти катети, якщо гіпотенуза дорівнює с.
С= 900), перпендикулярні. Знайти катети, якщо гіпотенуза дорівнює с.
(Відповідь: ![]() )
)
Задача 24. Знайти площу трикутника, сторонами якого є медіани трикутника з площею S.
(Відповідь: ![]() )
)
Задача 25. Довжини двох медіан трикутника дорівнюють 2 і 3. В яких межах може бути довжина третьої медіани? При якому її значенні площа трикутника найбільша і чому вона дорівнює?
(Відповідь: (1;5); ![]() ; 4)
; 4)
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Атанасян Л.С. Геометрия: учебник для 7-9 классов / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадоминцев. – М. : Просвещение, 1996. – 335с.
- Бевз Г.П. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів / Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова. – 2-ге вид. – Київ: Генеза, 2016. – 192с.
- Бевз Г.П. Геометрія: підручник для 8 класу загальноосвітніх навчальних закладів / Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова. – Київ: Освіта, 2016. – 272с.
- Бевз Г.П. Геометрія: підручник для 9 класу загальноосвітніх навчальних закладів / Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова. – Київ: Освіта, 2017. – 272с.
- Готман Э.Г. Задача одна – решения разные: учебное пособие / Э.Г.Готман, З.А.Скопец. – К. : Радянська школа, 1988. – 173с.
- Єршов А.П. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів / А.П.Єршов, В.В.Голобородько, О.Ф.Крижановський. – Харків: Ранок, 2015. – 224 с.
- Єршов А.П. Геометрія: підручник для 8 класу загальноосвітніх навчальних закладів /А.П.Єршов, В.В.Голобородько, О.Ф.Крижановський, С.В.Єршов. – 3-тє вид. – Харків: Веста, 2010. –
256 с.
- Єршов А.П. Геометрія: підручник для 9 класу загальноосвітніх навчальних закладів / А.П.Єршов, В.В.Голобородько, О.Ф.Крижановський, С.В.Єршов. – 7-ме вид. – Харків: Ранок, 2015. – 256 с.
- Кушнір І.А. Методи розв’язання задач з геометрії: книга для вчителя / І.А.Кушнір. – Київ: Абрис, 1994. – 461с.
- Кушнір І.А. Трикутник у задачах: навчальний посібник / І.А.Кушнір. – Київ: Либідь, 1994. – 104 с.
- Невар С.Э. Медиана треугольника. Оптимальные методы решения задач / С.Э.Невар // Государственное учреждение образования «Средняя школа № 12 г. Пинска». – 2016. – 29с. [Електронний ресурс]. – Режим доступу:
https://ds04.infourok.ru/uploads/.../000769f2-1e1be7a2.doc
- Прасолов В.В. Задачи по планиметрии: учебное пособие / В.В.Прасолов. – М.: Наука, 1986. – 272 с.
1


про публікацію авторської розробки
Додати розробку
