Тест з геометрії 7 клас "Суміжні кути"
1. Два кути називають суміжними, якщо…
а) одна сторона у них є спільною, а дві б) одна сторона у них є спільною, а дві інші сторони цих кутів - не спільні інші сторони цих кутів є
доповняльними
в) одна сторона у них є бісектрисою, а дві інші сторони цих кутів є доповняльними
2. Згідно з теоремою про властивість кутів, сума суміжних кутів дорівнює:
а) об) о 90160
в) 0ог) 180о
3. За наслідками з теореми про властивість суміжних кутів, кут, суміжний із прямим кутом, є
…
а) розгорнутимб) тупим
в) гостримг) прямим
4. За наслідками з теореми про властивість суміжних кутів, кут, суміжний із гострим кутом, є
…
а) прямимб) тупим
в) гостримг) розгорнутим
5. За наслідками з теореми про властивість суміжних кутів, кут, суміжний із тупим кутом, є …
а) прямимб) тупим
в) гостримг) розгорнутим
6. Якщо кути рівні, то суміжні з ними кути…
б) рівні
г) різні
|
|
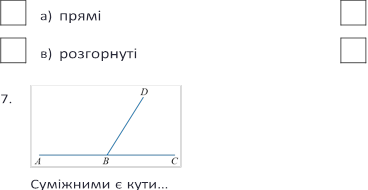
а) ∠ АВD і ∠ DВС
|
б) ∠ DВС і ∠ АВС |
|
|
в) ∠ АВD і ∠ АВС |
г) ∠ DВА і ∠ СВD |
|
8. |
Які з перелічених пар кутів - суміжні:
|
|
а) о об) о о
90 і 1091 і 89
в) о ог) о о
5 і 165166 і 14
9. Один із суміжних кутів на 42° більший від іншого. Які градусні міри цих кутів?
а) о об) о о
58 і 12269 і 111
в) о ог) о о
35 і 14512 і 168
10. Суміжні кути, якщо їх градусні міри відносяться як 4:5, дорівнюють …
а) о об) о о
80 і 100 20 і 80
в) о ог) о о
40 і 14040 і 50
Ключ до тесту
|
1. б (1 балів) |
2. г (1 балів) |
3. г (1 балів) |
4. б (1 балів) |
|
5. в (1 балів) |
6. б (2 балів) |
7. а г (2 балів) |
8. б г (2 балів) |
9. б (3 балів) 10. а (4 балів)
про публікацію авторської розробки
Додати розробку