Тест з теми "Переріз куба площиною, що проходить через три задані точки"
 Переріз куба площиною, що проходить через три задані точки
Переріз куба площиною, що проходить через три задані точки
Ключове питання: «Який многокутник може бути перерізом куба?»
Многокутник з числом сторін більше шести;
гострокутний, прямокутний або тупокутний трикутник; правильний трикутник; рівнобедрений трикутник;
паралелограм; прямокутник; ромб; квадрат;
трапеція; рівнобедрена трапеція; прямокутна трапеція;
п’ятикутник; правильний п’ятикутник; п’ятикутник з двома парами паралельних сторін;
шестикутник; шестикутник з однією віссю симетрії; правильний шестикутник.
Джерело:
1. #3. Как строить сечения многогранников? https://www.youtube.com/watch?v=JiwbTfJa3Y0
(Правильний трикутник, прямокутник, ромб, рівнобедрений трикутник).
2. Урок: Побудова перерізів многогранників. https://www.youtube.com/watch?v=ZaUrgVkkYHQ
(Правильний трикутник, рівнобедрена трапеція, ромб, п’ятикутник з двома парами паралельних сторін).
3. Презентація. Переріз куба https://naurok.com.ua/prezentaciya-pereriz-kuba-pobudova-pereriziv-metodom-slidiv-25407.html
4. Побудова перерізу куба. Шестикутник. https://www.youtube.com/watch?v=rcbUz8QT_lc
5. Площа перерізу куба. Шестикутник. https://www.youtube.com/watch?v=3hhpDBupN70
6. Перерізи многогранників. Побудова перерізів методом слідів https://disted.edu.vn.ua/courses/learn/10119
7. Многоугольники, получающиеся в сечении куба http://www.myshared.ru/slide/51318/
Задача. Точку N взято на ребрі CC1 куба ABCDA1B1C1D1. Доведіть, що переріз куба площиною BND1 - паралелограм.
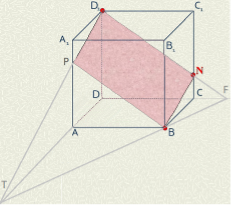 Розв’язання
Розв’язання
Січна площина проходить через три задані точки B, N і D1 куба ABCDA1B1C1D1.
І спосіб. D1N DC = F, FB DA = T, TD A1A = P.
ІІ спосіб. 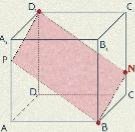 B (BCC1) і N (BCC1), тому BN (BCC1). N (DCC1) і
B (BCC1) і N (BCC1), тому BN (BCC1). N (DCC1) і
D1 (DCC1), тому ND1 (DCC1). Прямі перетину паралельних площин (ABB1) і (D1CC1) січною площиною – паралельні. Через точку B проводимо пряму, яка паралельна ND1. Точка P - перетин цієї прямої з ребром AA1. З’єднаємо точки P і D1. (BCC1) || (ADD1), тому BN || PD1. BND1P – паралелограм за означенням і шуканий переріз.
Виконати завдання (відкрийте вкладку Вставлення, натисніть кнопку Фігури, виберіть Лінія).
 1 (20101, 12). Перерізом куба ABCDA1B1C1D1 площиною, що проходить через точки A, C, C1 є
1 (20101, 12). Перерізом куба ABCDA1B1C1D1 площиною, що проходить через точки A, C, C1 є
|
А |
Б |
В |
Г |
Д |
|
прямокутний трикутник |
рівносторонній трикутник |
прямокутник |
ромб |
трапеція |
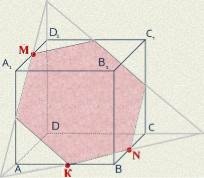
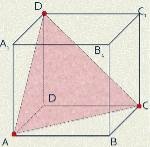
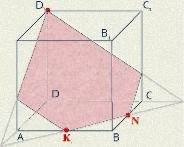
2 (2010П, 28). На рисунках (1-4) зображено куб і три точки, що є вершинами куба або серединами його ребер. Установіть відповідність між кожним рисунком (1-4) і назвою фігури (А-Д), що є перерізом куба площиною, що проходить через три задані точки. 1 2 3 4
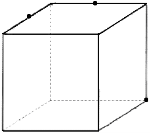
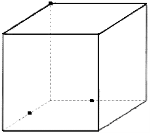
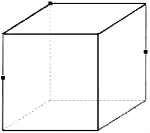
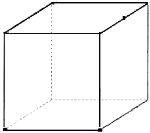
А трикутник Б прямокутник В трапеція Г п’ятикутник Д ромб
3. На рисунках (1-4) зображено куб і три точки, що є вершинами куба або серединами його ребер. Установіть відповідність між кожним рисунком (1-4) і назвою фігури (А-Д), яка є перерізом куба площиною, що проходить через три задані точки. 1 2 3 4
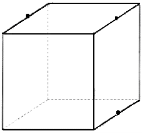
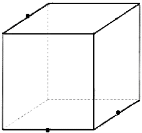

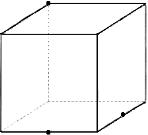
А трикутник Б квадрат В шестикутник Г п’ятикутник Д паралелограм
Відповіді (учителю для перевірки):
1 (20101, 12) В. 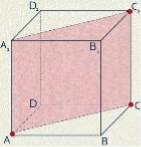 Прямокутник AA1C1C називають діагональним перерізом куба.
Прямокутник AA1C1C називають діагональним перерізом куба.
2 (2010П, 28). 1В, 2А, 3Д, 4Б.
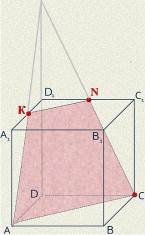
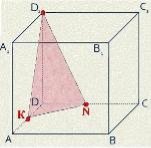
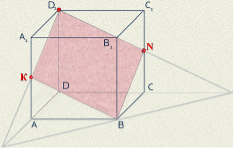
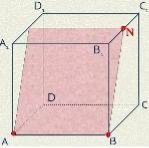
3. 1Б, 2В, 3А, 4Г. 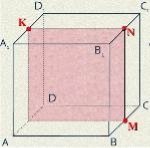


про публікацію авторської розробки
Додати розробку
