Тестові завдання для підготовки до ЗНО
Відділ освіти Чорноморської міської ради Одеської області Олександрівська загальноосвітня школа І-ІІІ ступенів Чорноморської міської ради Одеської області
Завдання на відповідність під час підготовки учнів до ЗНО як засіб реалізації компетентнісного підходу до навчання математики
Антіпа Наталя Степанівна,
учитель математики,
спеціаліст вищої категорії,
старший учитель
м.Чорноморськ
2020
Зміст
Вступ ......................………………………………...……........................3
Розділ 1. Вправи з алгебри 7-8 класи...........………...........................5
Розділ 2. Вправи з геометрії 7-8 класи........………....…...................10
Розділ 3. Вправи з алгебри 9 клас......................................................15
Висновки……… ………………………….………..............................29
Список літератури….…………………………… .....................…….30
Вступ
Займатися підготовкою учнів до ДПА та ЗНО з математики потрібно, на мою думку, починаючи ще з 5 класу. Ця підготовка заключається у знайомстві учнів з різними видами тестових завдань, систематичному повторенні матеріалу, що вивчається. Оскільки я викладаю математику у школі ІІ ступеню, маю досвід роботи щодо такої підготовки. Метою її є підготовка до складання державної підсумкової атестації за курс основної школи, а також підготовка до ЗНО після отримання учнями повної загальної середньої освіти. Успішне виконання учнями завдань зовнішнього незалежного оцінювання з математики спирається, перш за все, на успішне засвоєння ними як теоретичного матеріалу курсу математики, так і методів розв’язування задач, передбачених програмними вимогами.
Велику увагу приділяю повторенню навчального матеріалу, узагальненню та систематизації знань та навичок учнів. Обов’язково в домашнє завдання включаю завдання на повторення. На літні канікули учні отримують завдання за темами, які були вивчені в поточному навчальному році з метою повторення та більш глибокого засвоєння матеріалу. Знайомство учнів із форматами тестових завдань починаю в 5 класі (самостійні роботи, експрес-оцінювання, контрольні роботи тощо). В основному це завдання з вибором однієї чи кількох правильних відповідей, завдання з короткою та розгорнутою відповідями. Завдання на відповідність та встановлення правильної послідовності пропоную учням вже у 8-9 класах.
З геометрії особливу увагу приділяю повторенню формул площ та об’ємів геометричних фігур, основних теорем, таких як терема Піфагора, теореми синусів, косинусів та застосуванню їх для розв’язування задач. Для кожної з тем роблю підбірку завдань за принципом від легких до складних. Часто при вивченні нового матеріалу пропоную дітям завдання практичного характеру, графічні вправи для формування в них навичок правильної побудови малюнка до задачі, читання готових креслень тощо. Особливу увагу приділяю повторенню основних геометричних та алгебраїчних формул. Для цього проводжу математичні диктанти на знання формул, усні заліки. Для виконання вдома пропоную учням завдання для самостійного розв’язання у вигляді домашніх контрольних робіт та тестові завдання. Для самоконтролю учням можна надати правильні відповіді або перевірити на наступному уроці. Також практикую підготовку до ДПА он-лайн, декілька учнів протягом уроку та після нього можуть спробувати свої сили та оцінити отриманий результат. Це достатньо стимулює учнів, щоб наступного разу здобути ще більше балів. Також учні можуть вдома самостійно проходити он лайн-тестування, а потім звітують про свої результати. При виникненні утруднень, розв’язуємо завдання тестів в класі. Для контролю знань використовую тести двох видів «вибери відповідь із запропонованих» та «напиши вірну відповідь». Завдання контрольних робіт для 9 класу намагаюся проводити у формі максимально наближеної до ДПА та ЗНО, обов’язково включаю завдання з одним правильним варіантом відповіді, завдання на встановлення відповідності. Оскільки розв’язування задач під час виконання тесту ЗНО не передбачає застосування калькуляторів та інших обчислювальних засобів, то удосконалення вмінь та навичок усних та письмових обчислень необхідно здійснювати на кожному уроці математики. З цією метою на початку більшості своїх уроків я пропоную учням вправи на усний рахунок («Морський бій», числові ребуси, змагання Прангліміне тощо).
Отже, підсумовуючи сказане, необхідно знайомити учнів з технікою тестування, привчати їх виконувати завдання не лише правильно, але й швидко, постійно контролюючи час, щоб максимально наблизити їх до умов, у яких випускники працюватимуть під час державної підсумкової атестації та зовнішнього оцінювання. Також якісна підготовка до ДПА та ЗНО передбачає організацію самоосвітньої діяльності учнів щодо повторення курсу математики під керівництвом учителя.
Завдання на встановлення відповідності (логічні пари) складається зі спільного вступного запитання та чотирьох завдань, позначених буквами (або цифрами), до кожного з яких потрібно дібрати один варіант відповіді. Як правило, такі завдання мають 4 основи та 5 - 6 варіантів вибору до них.
Розділ 1. Вправи з алгебри 7-8 класи
1. Установити відповідність між виразами (1-4) та тотожно рівними їм виразами (А-Д):
1) (а – b)(а + b ) А) a³ -b³
2) (а + b)( a²– аb +b²) Б) a² -b²
3) (а – b)(a²+ аb + b²) В) ( a+b)²
4) a²+2аb + b² Г) a³ + b³
Д) a² + b²
2. Установити відповідність між виразами (1-4) та тотожно рівними їм виразами (А-Д):
1) 3(5х -7) + 14 А) 2х
2) (х + 5) – (2х +7) Б) -х - 2
3) 10х - 4(2 +3х) В) 15х -7
4) (-5 + х +у) – (х – у -5) Г ) -8 – 2х
Д) 22х – 8
3. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
1) х = 18 -2х А) 8
2) 3(х -5) = х + 1 Б) 6
3) ![]() х = 10 В) немає розв` язку
х = 10 В) немає розв` язку
4) |x| = -7 Г) 3
Д ) 14
4. Установити відповідність між виразами (1-4) та їх значеннями (А-Д):
1) a5· a3 А) a2
2) (a3 )5 Б) a8
3) a5 : a3 В) (аb )10
4) а5 . b5 Г) a15
Д) (аb )5
5. Установити відповідність між виразами (1-4)та їх розкладами на множники (А-Д):
1) а12 + а3 А) (а + b)(3 – х)
2) а(m +n) – в(m + n) Б) (а4 + 1)
3) 3а +3b – ах - bх В) а3(а9 + 1)
4) 3х3 - 3х2 а Г) (а – b)(m + n)
Д) 3х2 (х – а)
6. Установити відповідність між виразами (1-4)та їх розкладами на множники (А-Д):
- х2 + х – 2 А) (х + 3)(х – 2)
- х2 + х – 6 Б) (х – 1)(х + 2)
- х2 - 5х – 6 В) (х – 6)(х + 1)
- х2 – х – 2 Г) (х + 1)(х – 2)
Д) (х + 6)(х + 1)
7. Установити відповідність між назвою функції(1-4) та функцією (А-Д):
1) лінійна функція А) у = 4х2
2) обернена пропорційність Б) у = 2х + 3
3) квадратична функція В) у = 8
4) пряма пропорційність Г) у = 7х
Д) у = -![]()
8. Установити відповідність між рівняннями (1-4) та виразами однією змінною через другу (А-Д):
- 2х + 4у = 8 А) у = -3у - 1
-
3х – 9у = -3 Б) у =
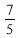 –
– 
- 5у + 2х = 7 В) х = 4 – 2у
-
2у – 7х = 5 Г) у =
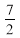 х +
х + 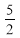
Д) х = 3у — 1
9. Установити відповідність між рівностями з двома змінними (1-4) та парою чисел, яка є розв’язком (А-Д):
1) х + 3у = 1 А) (0; -7)
2) 2х –у = 7 Б) (-2; -6)
3) 5х – 3у = -4 В) (-2; 1)
4) -7х + 4у = -10 Г) (2; -6)
Д) (4; 8)
10. Установити відповідність між формулою (1-4) та точкою перетину з віссю Ох (А-Д):
- у = 2х – 3 А) (2; 0)
- у = -5х + 2 Б) (-0,5; 0)
- 3х – 4у = 6 В) (0,4; 0)
- -2у – 8х = 4 Г) (0;2)
Д) (1,5; 0)
11. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
1) ![]() = 5 А) -3
= 5 А) -3
2) ![]() =
= ![]() Б) 7
Б) 7
3) ![]() =
= ![]() В)
В) ![]()
4) ![]() х =
х = ![]() Г) 7,5
Г) 7,5
Д ) -0,75
12. Установити відповідність між виразами (1-4) та тотожно рівними їм виразами (А-Д):
1) (а +1)(а -1)(a²+1) А) 2a2 +18
2) (а + 3)² +( а -3)² Б) a4 +1
3) (2 – ![]() )² −
)² −![]() В) 4 −
В) 4 − ![]()
4) 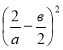 Г) a4 −1
Г) a4 −1
Д) ![]()
13. Установити відповідність між виразами (1-4) та тотожно рівними їм виразами (А-Д):
-
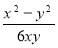 ·
· 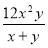 А) 1,5
А) 1,5
-
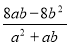 ·
· 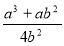 Б)
Б) 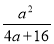
-
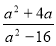 ׃
׃ 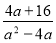 В) 2х(х + 4у)
В) 2х(х + 4у)
-
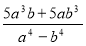 :
: 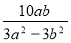 Г) 2х2 – 2ху
Г) 2х2 – 2ху
Д ) ![]()
14. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
- x2 = 7 А) немає розв` язку
- x2 - 2 = 7 Б) х = ±7
-
|x|= -7 В) х = ±
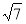
-
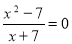 Г) х = 7
Г) х = 7
Д) х = 3
15. Установити відповідність між системою рівнянь (1-4) та парою розв’язків цих систем (А-Д):
1) ![]() А) (1; 2)
А) (1; 2)
2) ![]() Б) (4; 3)
Б) (4; 3)
3) ![]() В) (5; 2)
В) (5; 2)
4) ![]() Г) (-2; 3)
Г) (-2; 3)
Д) (2; 2)
16. Установити відповідність між функцією (1-4) і її кутовим коефіцієнтом (А-Д):
-
у = -2х +
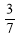 А) к =
А) к = 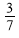
-
у =
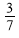 х – 2 Б) к = 2
х – 2 Б) к = 2
-
7х + 3у = 2 В) к = -
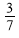
- -3х – 7у = -2 Г) к = - 2
Д ) к = -![]()
17. Установити відповідність між виразами (1-4) та їх значеннями (А-Д):
1) ![]() А)
А) ![]()
2) ![]() Б)
Б) ![]()
3) ![]() В)
В) ![]()
4) ![]() Г)
Г) ![]()
Д) ![]()
18. Установити відповідність між виразами (1-4) та їх значеннями(А-Д):
-
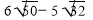 А)
А) 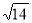
-
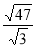 Б) 10
Б) 10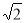
-
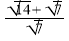 В) 7
В) 7
-
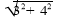 Г)
Г)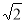 + 1
+ 1
Д) 5
19. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
-
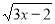 = 4 А) 36
= 4 А) 36
-
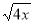 + 2 =0 Б) 6
+ 2 =0 Б) 6
-
6 -
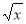 = 0 В) 64
= 0 В) 64
-
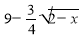 = 3 Г) немає розв` язку
= 3 Г) немає розв` язку
Д) -62
20. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
- 3х2 - 12 = 0 А) немає розв` язку
- х2 + 2х = 0 Б) ±2
- х2 = -2,5 В) 0; - 2
- 4х2 – 25 = 0 Г) ± 2,5
Д) 4
21. Установити відповідність між виразами (1-4) та їх значеннями (А-Д):
-
 А) - 6
А) - 6
-
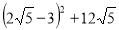 Б) 6
Б) 6
-
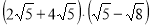 В) 3
В) 3
-
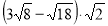 Г) 2
Г) 2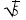
Д) 29
22. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
1) х2 – 7х + 10 = 0 А) - 2; 5
2) х2 – 3х – 10 = 0 Б) 2; 5
3) х2 + 3х – 10 = 0 В) 2; - 5
4) х2 + 7х + 10 = 0 Г) 10; 7
Д) - 2;- 5
23. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
- х2 – 9х + 20 = 0 А) - 4; 5
- х2 – х - 20 =0 Б) - 4; - 5
- х2 +х – 20 = 0 В) 4; 5
- х2 + 9х + 20 = 0 Г) 1; 20
Д) 4; - 5
24. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д) :
-
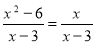 А) - 4; 3
А) - 4; 3
-
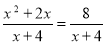 Б) 2
Б) 2
-
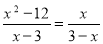 В) 3
В) 3
-
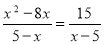 Г) - 4
Г) - 4
Д) - 2
Розділ 2. Вправи з геометрії 7-8 класи
Установити відповідність між величинами (1-4), та їх значеннями (А-Д)
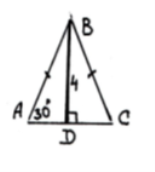
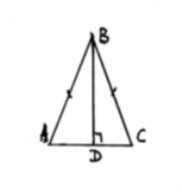
1. 1) Знайти АВ А) ![]()
2) Знайти АС Б) ![]()
3) Знайти SАВС В) ![]()
4) Знайти РАВС Г) 8
Д) ![]()
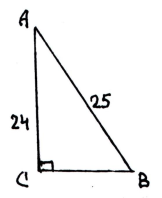
 2. Дано: РАВС = 36; АС = 10
2. Дано: РАВС = 36; АС = 10
1) Знайти АВ А) ![]()
2) Знайти ВД Б) 13
3) Знайти SАВС В) ![]()
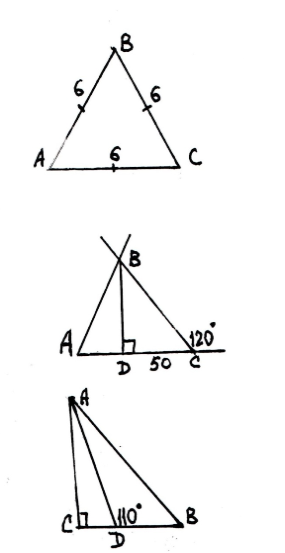 4) Знайти sin C Г) 12
4) Знайти sin C Г) 12
Д) 60
3. 1) Знайти SАВС А) ![]()
2) Знайти R Б) ![]()
3) Знайти r В) ![]()
4) Знайти cos A Г) ![]()
Д) 0,5
4. 1) Знайти кут А А) 100º
2) Знайти кут В Б) 60º
3) Знайти кут С В) 40º
4) Знайти ВС Г) 80º
Д) 120º
5. Дано: АД - бісектриса кута
1) Знайти кут СДА А) 20º
2) Знайти кут В Б) 70º
 3) Знайти кут САД В) 50º
3) Знайти кут САД В) 50º
4) Знайти кут САВ Г) 80º
Д) 40º
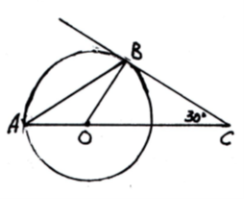
6. 1) Знайти кут ОВС А) 60º
2) Знайти кут ВОС Б) 30º
3) Знайти кут АОВ В) 90º
4) Знайти кут АВО Г) 150º
Д) 120º
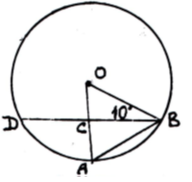
7. Дано: ВС=СД; кут ОВС=10º
1) Знайти кут АОВ А) 40º
2) Знайти кут ОАВ Б) 50º
3) Знайти кут АВС В) 80º
4) Знайти кут ОСВ Г) 120º
Д) 90º
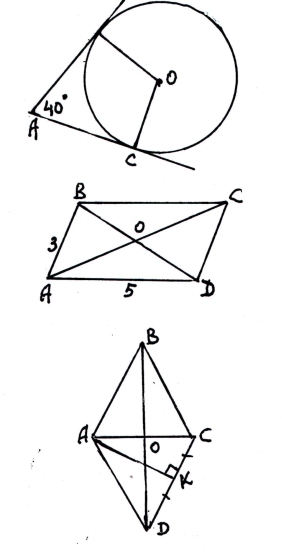 8. 1) Знайти кут ВАО А) 90º
8. 1) Знайти кут ВАО А) 90º
2) Знайти кут ОВА Б) 20º
3) Знайти кут ВОА В) 140º
4) Знайти кут ВОС Г) 120º
Д) 70º
9. Дано: АВСД - паралелограм; кут А=60º
1) Знайти SАВСД А) 16
2) Знайти ВД Б) 7
3) Знайти АС В) 7,5![]()
4) Знайти РАВСД Г) ![]()
Д) 15
10. Дано: К - середина ДС; ДК=5
1) Знайти кут АДС А) 10
2) Знайти АС Б) 10![]()
3) Знайти ВД В) 100
4) Знайти SАВСД Г ) 60
Д ) 50![]()
11. Дано: АВСД - прямокутник; АО -
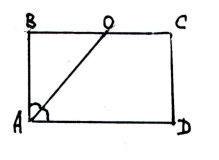 бісектриса кута А, ВО : ОС=5:7; РАВСД =34.
бісектриса кута А, ВО : ОС=5:7; РАВСД =34.
1) Знайти АД А) 5
2) Знайти АВ Б) 13
3) Знайти ВД В) 17
4) Знайти SАВСД Г) 12
Д) 60
 12. 1) Знайти СВ А)
12. 1) Знайти СВ А) ![]()
2) Знайти sin A Б) ![]()
3) Знайти cos A В) 7
4) Знайти tg А Г) ![]()
 Д)
Д) ![]()
13. 1) Знайти СД А) 10
2) Знайти АС Б) 8![]()
3) Знайти ВС В) 8
4) Знайти SАВС Г) 4![]()
Д) 80
14. 1) Знайти СВ А) 9
2) Знайти АД Б) 15
3) Знайти SАВС В) 130
4) Знайти АС Г) 150
Д) 20
 15. 1) Знайти АС А) 6
15. 1) Знайти АС А) 6![]()
2) Знайти ВС Б) 2![]()
3) Знайти SАВС В) 7,5
4) Знайти SАСД Г) 3,5![]()
Д) ![]()
 16. 1) Знайти АС А) 18
16. 1) Знайти АС А) 18![]()
2) Знайти SАСД Б) 12
3) Знайти SАВС В) 9
4) Знайти середню Г) 36
лінію трапеції АВСД Д) 36![]()
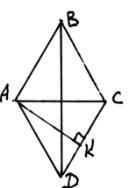 17.Дано: АВСД - ромб; ВД=24; АС=18
17.Дано: АВСД - ромб; ВД=24; АС=18
1) Знайти РАВСД А ) 14,4
2) Знайти SАВСД Б) 60
3) Знайти АК В) 7,2
4) Знайти r Г) 216
Д) 120
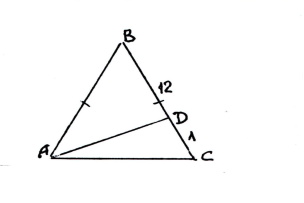 18. Дано:АВ=ВС
18. Дано:АВ=ВС
1) Знайти АС А) 32,5
2) Знайти SАВС Б) ![]()
3) Знайти АД В) 65
4) Знайти tg САД Г) 5
 Д)
Д)![]()
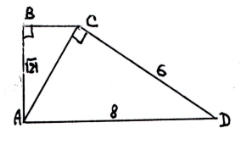
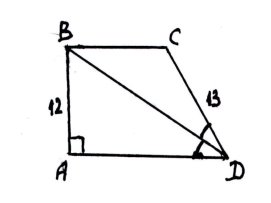
19. Дано: АВСД - прямокутна трапеція,
АВ=12, СД=13, ДВ- бісектриса кута Д.
1) Знайти ВС А) 18
2) Знайти АД Б) 186
3) Знайти SАВСД В) 13
4) Знайти ВД Г) 6
Д) 20
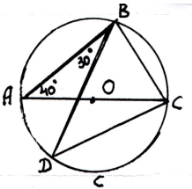 20. 1) Знайти кут АСД А) 60º
20. 1) Знайти кут АСД А) 60º
2) Знайти кут АВС Б) 30º
3) Знайти кут ДВС В) 90º
4) Знайти кут ВДС Г) 80º
Д ) 40º
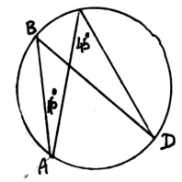 21.1) Знайти кут В А) 15º
21.1) Знайти кут В А) 15º
2) Знайти кут Д Б) 45º
3) Знайти кут ВОА В) 120º
4) Знайти кут АОД Г) 60º
Д) 80º
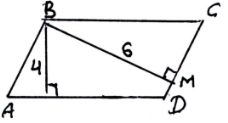 22. Дано: АВСД - паралелограм; ДС= 8
22. Дано: АВСД - паралелограм; ДС= 8
1) Знайти АД А) 48
2) Знайти SАВСД Б) 4
3) Знайти АК В) 12
4) Знайти МС Г) 8
 Д) 6
Д) 6
23. Дано: АВСД – трапеція; кут АС = 90º
ВС = 12; АД = 20; А = СД
1) Знайти висоту АВСД А) 8
2) Знайти SАВСД Б) 4
3) Знайти АС В) 128 4) Знайти АВ Г) 20
Д) 8
Розділ 3. Вправи з алгебри 9 клас
1. Установити відповідність між квадратними рівняннями (1-4) та сумою їх коренів (А-Д):
1) х2 +5х+4=0 А) 2
2) х2 - 2х+3=0 Б) -5
3) х2 +7х - 4=0 В) 7
4) х2 +2х- 1=0 Г) -7
Д) -2
2. Установити відповідність між графіками функцій (1-4) та абсцисами точки перетину з віссю Ох (А-Д):
1) у = х2 -3х -6 А) 0
2) у = х2 - 1 Б) -2 і 3
3) у = х2 -2х - 3 В) 1 і -1
4) у = х2 -4х +3 Г) -1 і 3
Д) 3 і 1
3. Установити відповідність між графіками функцій (1-4) та абсцисами точки перетину з віссю Оу (А-Д):
1) ![]() А) 2
А) 2
2) ![]() Б) 0
Б) 0
3) ![]() В) 1
В) 1
4) ![]() Г) -2
Г) -2
Д) 3
4. Установити відповідність між функцією (1-4) та місцем знаходження вершини параболи (А-Д):
1) у=(х-1)2 А) в початку координат
2) у=х2 -1 Б) на осі Ох
3) у=х2 В) на осі Оу
4) у= -х2 +5 Г) в І чверті
Д) в ІІІ чверті
5. Установіть відповідність між нерівністю (1-4) та її розв'язком (А-Д):
1) x2 – 2x -15![]() А) [0;3]
А) [0;3]
2) ![]() Б) [-3;5]
Б) [-3;5]
3) ![]() В) (-∞;-5]⋃ [5;+∞)
В) (-∞;-5]⋃ [5;+∞)
4) ![]() Г) (-∞;-3]⋃ [5;+∞)
Г) (-∞;-3]⋃ [5;+∞)
Д) (-∞;3)⋃ (3;+∞)
6. Установити відповідність між графіками функцій (1-4) та абсцисами точки перетину з віссю Ох (А-Д):
1) у = -2 х2 +3х +5 А) 1 і 3
2) у = -х2 +5 Б) 2 і 4
3) у = 7 х2 +4х - 9 В) 4
4) у = 5 х2 +2х +3 Г) 2
Д) 3
7. Установити відповідність між парами функцій(1-4) та їх точками перетину (А-Д):
1) у = 1 і у = ![]() А) (0;5)
А) (0;5)
2) у = -х і у = ![]() Б) (2;4)
Б) (2;4)
3) ![]() і у = 2 В) (4;2)
і у = 2 В) (4;2)
4) у = -х2 +5 і у = 5 Г) не перетинаються
Д) (5;1)
8. Установити відповідність між парами функцій (1-4) і точками їх перетину (А-Д):
1) ![]() і
і![]() А) (0; 5)
А) (0; 5)
2)![]() і
і![]() Б) (-1; 1)
Б) (-1; 1)
3)![]() і
і ![]() В) (3; 5)
В) (3; 5)
4)![]() і
і ![]() Г) (1; 2)
Г) (1; 2)
Д) (3; 1)
9. Установити відповідність між нерівністю (1-4) та кількістю цілих розв'’зків (А-Д):
1) -2x2 + 5x + 10 >0 А) 1
2) 3x2 – 5x +2<0 Б) 0
3) ![]() В) 1 і 2
В) 1 і 2
4) x2 + 2x +3<0 Г) розв'язків не має
Д) 2 і 3
11. Установити відповідність між нерівністю (1-4) та цілими розв’язками нерівностей (А-Д):
1) x2 – 1< 0 А) 3, 4 і 5
2) - x2 + x + 2 > 0 Б) 0
3) x2 - 8x +15 > 0 В) -3 ; -2
4) x2 + 5x +6 < 0 Г) 5; 6
Д) 1
12. Установити відповідність між рівняннями(1-4) та кількостю їх розв’язків (А-Д):
1) х2-7х+10=0 А) один
2) х2+8х+16=0 Б) два
3) (х2 -1)(х2 -5)=0 В) жодного
4) х2+5х+7=0 Г) три
Д) безліч
13. Установити відповідність між виразами (1-4) та їх розкладами на множники (А-Д):
1) 2х2+4х - 6 А) (х-3)(х+2)
2) х2 - х - 6 Б) 3(х+2)(х-5)
3) 3х2 -9х -30 В) 2(х-1)(х+3)
4) х2-4 Г) (х-4)(х+4)
Д) (х+2)(х-2)
14. Установити відповідність між функціями(1-4) та проміжками зростання або спадання(А-Д):
1) ![]() А) зростає на [2;+∞)
А) зростає на [2;+∞)
2) у = ![]() Б) спадає на (-∞; 3,5]
Б) спадає на (-∞; 3,5]
3) у = -х2 +3,5 В) спадає на всій області визначення
4) у = х2 -7х+10 Г) зростає на (-∞; 0]
Д) спадає на [10;+∞)
15. Установити відповідність між функцією (1-4) та її найбільшим значенням (А-Д):
1) у = - х2 +4х -3 А) 2
2) у = -х2 +2х +1 Б) 3
3) у = -х2 -4х - 1 В) 1
4) у = -х2 -2х -3 Г) -3
Д) -2
16. Установити відповідність між функцією (1-4) та її найменшим значенням (А-Д):
1) у = х2 -6х -3 А) -4
2) у = х2 - 2 Б) -2
3) у = х2 +2х - 3 В) -1
4) у = х2 -6х +11 Г) 0
Д) 2
17. Установити відповідність між квадратною функцією (1-4) та координатами вершини параболи (А-Д):
1) у = (х+5)2 -3 А) (-5; -3)
2) у = (х-5)2 -3 Б) (5; -3)
3) у = (х+3)2 -5 В) (-3; -5)
4) у = (х-3)2 -5 Г) (3; 3)
Д) (3; -5)
18. Установити відповідність між квадратним рівнянням (1-4) та дискримінантом квадратного рівняння (А-Д):
1) 2х2-3х+1=0 А) D=0
2) 8у2+4у+0,5=0 Б) D=16
3) х2 -5х +8=0 В) D=8
4) -х2-2х+1=0 Г) D=1
Д) D=-7
19. Установити відповідність між функціями (1-4) та ординатами вершини параболи (А-Д):
1) у = (х-2)2 А) 1
2) у = х2 -2 Б) 2
3) у = (х+2)2 В) 1 і 3
4) у = (х-2)2 +5 Г) 2 і 4
Д) 1 і 4
20. Установити відповідність між функціями (1-4) та геометричним перетворенням графіка функції у = х2 (А-Д):
1) у = (х-2)2 + 3 А) на 3 одиниці вправо і на 3 одиниці вгору
2) у = (х-2)2 -3 Б) на 2 одиниці вправо і на 3 одиниці вгору
3) у = (х+3)2 +2 В) на 2 одиниці вправо і на 2 одиниці вниз
4) у = (х-3)2 +3 Г) на 3 одиниці вліво і на 2 одиниці вгору
Д) на 2 одиниці вправо і на 3 одиниці вниз
21. Установити відповідність між квадратними рівняннями (1-4) та їх коренями (А-Д):
- х2 - 12х +20=0 А) 6 і -4
- х2 - 7х +12=0 Б) -2 і -3
- х2 - 5х + 6 =0 В) -6 і 3
- х2 + 3х -28 =0 Г) 6 і 1
Д) 5 і 1
22. Установити відповідність між квадратними рівняннями (1-4) та їх коренями (А-Д):
- х2 + 3х – 18=0 А) 6 і -4
- х2 - 2х – 14=0 Б) -2 і -3
- х2 + 5х + 6 =0 В) -6 і 3
- х2 – 6х + 5 =0 Г) 6 і 1
Д) 5 і 1
23. Установити відповідність між рівняннями (1-4) та їх коренями (А-Д):
- х2 + х – 72 =0 А) 8 і -9
- х2 - х – 56 =0 Б) -7 і 8
- х2 - х – 72 =0 В) -8 і
- х2 + х – 56 =0 Г) -8 і 7
Д) 7 і 8
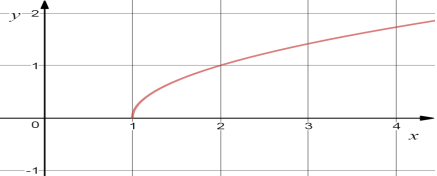
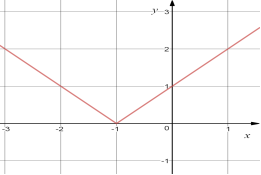
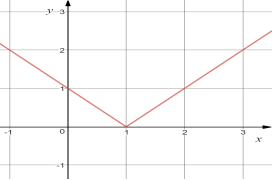
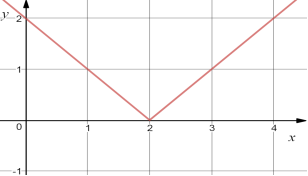
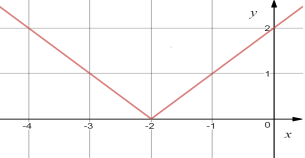
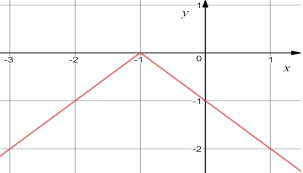
24.Установіть відповідність між графіком (1-4) та функцією (А-Д):
|
1) |
|
А) |
|
|
2) |
|
Б) |
|
|
3) |
|
В) |
|
|
4) |
|
Г) |
|
|
|
|
Д) |
|
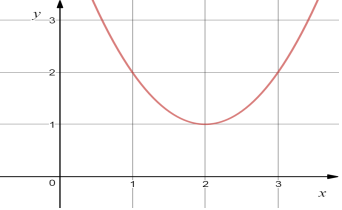
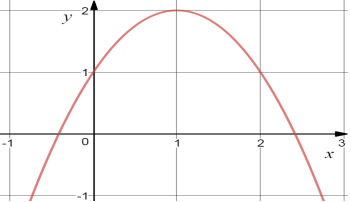
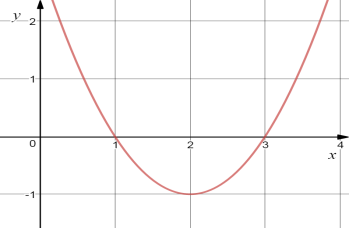
25. Установити відповідність між графіком (1-4) та функцією (А-Д):
|
1) |
|
А) |
у = -(х-1)2 +2 |
|
2) |
|
Б) |
у = -(х+2)2 +1 |
|
3) |
|
В) |
у = (х-2)2 +1 |
|
4) |
|
Г) |
у = (х-2)2 -1 |
|
|
|
Д) |
у = (х-1)2 -2 |
26. Установити відповідність між нерівностями (1-4) та їх розв'язками (А-Д):
1) ![]() А) [-2; 0)
А) [-2; 0)
2) ![]() Б) (-1; 0)⋃ (0; 1)
Б) (-1; 0)⋃ (0; 1)
3) – x2 + 2x ≥0 В) [0; 2]
4) ![]() Г) (0; 1)
Г) (0; 1)
Д) (-∞;-2]⋃ (0;+∞)
27. Установити відповідність між фунціями (1-4) та кординатами точок перетину їх графіків (А-Д):
1)![]() і
і![]() А) (-1;1)
А) (-1;1)
2)![]() і
і![]() Б) (1; 2)
Б) (1; 2)
3)![]() і
і ![]() В) (1; 1)
В) (1; 1)
4)![]() і
і ![]() Г) (- 2; 2)
Г) (- 2; 2)
Д) (1; 2)
28. Установити відповідність між рівняннями (1-4) та їх найбільшими коренями (А-Д):
1) х2 +4х-5=0 А ) 3
2) х2 -х-6=0 Б) 1
3) х2 -х-2=0 В) -1
4) х2 +4х+3=0 Г) 5
Д) 2
29. . Установити відповідність між рівняннями (1-4) та їх найменшими коренями (А-Д):
1) х2 -4х+3=0 А) 0
2) х(х -9)=0 Б) -4
3) 3х2 -48=0 В) 1
4) х2 -4=0 Г) 9
Д ) -2
30. Установити відповідність між нерівностями (1-4) та найбільшими їх цілими ї розв’язками (А-Д):
1) ![]() А) розв'язків немає
А) розв'язків немає
2) ![]() < 0 Б) -1
< 0 Б) -1
3) ![]() В) 1
В) 1
4) x2 – 2<0 Г) 5
Д) 2
31. Установити відповідність між нерівностями (1-4) і їх розв’язками (А-Д):
1)![]() А) [-9; 7]
А) [-9; 7]
2) ![]() Б) [0; 3]
Б) [0; 3]
3) ![]() В) (-∞;1) ⋃ (5;+∞)
В) (-∞;1) ⋃ (5;+∞)
4) ![]() Г) (-∞; -3] ⋃ [1;+∞)
Г) (-∞; -3] ⋃ [1;+∞)
Д) (4; 12)
32. Установити відповідність між нерівностями (1-4) і їх найменшими цілими розв’язками (А-Д):
1) 2х2 – 5х+2<0 А) 2
2) -2х2+3х+2>0 Б) 0
3) ![]() В) -1
В) -1
4) ![]() Г) 1
Г) 1
Д) розв'язків не має
33. Установити відповідність між нерівностями (1-4) та їх розв’язками (А-Д):
1) ![]() А) (-2;5)
А) (-2;5)
2) ![]() Б) [-5;2)
Б) [-5;2)
3) ![]() В) (-∞;-2)⋃ [3;+∞)
В) (-∞;-2)⋃ [3;+∞)
4) ![]() Г) (-∞; -5]⋃ (2;+∞)
Г) (-∞; -5]⋃ (2;+∞)
Д) (-3;2)
34. Установити відповідність між нерівностями (1-4) та їх розв’язками (А-Д):
1) ![]() А) [-4;-3)⋃ (-3;2]
А) [-4;-3)⋃ (-3;2]
2) ![]() Б) [-7;1)⋃ (1;3]
Б) [-7;1)⋃ (1;3]
3) ![]() В) [3;4)⋃ (4;5]
В) [3;4)⋃ (4;5]
4) ![]() Г) [2;8)⋃ (8;9]
Г) [2;8)⋃ (8;9]
Д) [-1;2)⋃ (2;3]
35. установити відповідність між функціями (1-4) та областю визначення функції (А-Д):
1)![]() А) (-∞;6)⋃ (6;+∞)
А) (-∞;6)⋃ (6;+∞)
2)![]() Б) (-∞;2)⋃ (2;3 )⋃(3;+∞)
Б) (-∞;2)⋃ (2;3 )⋃(3;+∞)
3)![]() В) (-∞;0)⋃(0;+∞)
В) (-∞;0)⋃(0;+∞)
4) ![]() Г) (-∞;0]⋃ [7;+∞)
Г) (-∞;0]⋃ [7;+∞)
Д) (-∞;+∞)
36. Установити відповідність між нерівностями (1-4) та їх цілими розв’язками (А-Д):
1)![]() А) -2; -1; 0; 1
А) -2; -1; 0; 1
2) ![]() Б) 0
Б) 0
3) ![]() В) 4 і 5
В) 4 і 5
4) ![]() Г) 2 і 3
Г) 2 і 3
Д) розв'язків не має
37. Установити відповідність між системою нерівностей (1-4) та їх цілими розв’язками (А-Д):
1) ![]() А) - 5
А) - 5
2) ![]() Б) розв'язків немає
Б) розв'язків немає
3) ![]() В) 3
В) 3
4) ![]() Г) -1; 0; 1
Г) -1; 0; 1
Д) 2; 3; 4
38. Установити відповідність між дробами (1-4) та їх відповідними значеннями (А-Д):
1)![]() А)
А) ![]()
2)![]() Б)
Б) ![]()
3)![]() В)
В) ![]()
4)![]() Г)
Г) ![]()
Д) ![]()
39. Установити відповідність між рівняннями(1-4) та їх кореннями (А-Д):
1) (x+2)(x – 4) = x2 +2 А) -4
2) (x +1)(x-3) = x2 +5 Б) ![]()
3) (x+2)2 =(x-4)(x+3) В) - 5
4) (x+3)2=(x+5)(x-4) Г) -3
Д)![]()
40. Установити відповідність між дробами (1-4) та їх відповідними значеннями (А-Д):
1) ![]() А)
А) ![]()
2) ![]() Б)
Б) ![]()
3) ![]() В)
В) ![]()
4) ![]() Г)
Г) ![]()
Д) ![]()
41. Установити відповідність функціями (1-4) та відповідними проміжками області визначень (А-Д):
1)![]() А) (-∞;0)⋃ (5;+∞)
А) (-∞;0)⋃ (5;+∞)
2)![]() Б) (0;1)⋃ (1;2)
Б) (0;1)⋃ (1;2)
3)![]() В) (0; 1)
В) (0; 1)
4)![]() Г) (1;2)⋃ (3;5)
Г) (1;2)⋃ (3;5)
Д) (1;2)⋃ (2;3)
42. Установити відповідність між нерівностями (1-4) та множинами їх розв’язків (А-Д):
1) 3 < x – 2 < 5 А) (-7; - 5)
2) 3 < x + 2 < 5 Б) (- 3; - 1)
3) 3 < - x – 2 < 5 В) (-1; 3)
4) 3 < - x + 2 < 5 Г) (1; 3)
Д) (5; 7)
43. Установити відповідність між системами нерівностей (1-4) та відповідними проміжками розв’язків (А-Д):
1) ![]() А) (1;5)
А) (1;5)
2) ![]() Б) (1;3)
Б) (1;3)
3) ![]() В) (1;4)
В) (1;4)
4) ![]() Г) (3;5)
Г) (3;5)
Д) (3;4)
44. Установіть відповідність між нерівностями (1-4) та множинами їх розв’язків (А-Д):
1) ![]() А) [-4; 2)
А) [-4; 2)
2) ![]() Б) [-1;4)⋃ (4;5]
Б) [-1;4)⋃ (4;5]
3) ![]() В) [-2;2)⋃ (2;8]
В) [-2;2)⋃ (2;8]
4) ![]() Г) [-2;2)⋃ (2;4]
Г) [-2;2)⋃ (2;4]
Д) [3;4)⋃ (4;5]
45. Знайти відповідність між функцією та її графіком:
|
1)у = |
А)
|
|
|
2) y = |
Б) |
|
|
3 y = |
В) |
|
|
Г) |
|
|
|
Д) |
|
Висновки
Під час навчання математики – головне: навчити дитину аналізувати зміст завдання, щоб вона побачила оту «родзинку», від якої залежить весь розв`язок. Цій меті і відповідають вправи на встановлення відповідності, тому що їх розв`язування вимагає не тільки виконання математичних розрахунків, але й вміння аналізувати подану математичну інформацію.
Пропоновані тестові завдання дозволяють мені під час уроку за короткий час перевірити об’єм вивченого матеріалу, швидко діагностувати оволодіння учнями основного рівня підготовки з окремих навчальних тем.
Дані тести можна використовувати як для індивідуальної перевірки, так і окремими завданнями на самостійних чи контрольних роботах.
Список літератури
- Алгебра: підруч. для 8 кл. загальноосвітн. навч. закл. / О.С. Істер - К.: Освіта, 2008.- 208 с.
- Мерзляк А.Г., Полонський М.С., Рабінович Ю.М., Якір М.С. Збірник задач і завдань для тематичного оцінювання з алгебри для 9 класу. - Харків, Гімназія, 2004.- 160 с.
- Математика. Комплексне видання: Довідник з математики. 5-11класи. Аналіз найпоширених помилок. Тести/ О.С.Будна, С.М.Будна, А.Р.Гальперина, М.Я.Забелишинська, Ю.О.Захарченко, О.В. Школьний.-4-те вид., перероб. і доп.-К.: “Літера ЛТД”, 2012.-336 с..
- Підсумкові контрольні роботи для ДПА з математики. 9 клас/М.В.Березняк.-Тернопіль: Підручники і посібники, 2015.-64 с.
- Геометрія. 8 клас: Збірник самостійних і контрольних робіт/ А.П. Єршова, В.В. Голобородько, О.Ф. Крижановський.-2-ге ви.-Ч.: Веста Видавництво “Ранок”-2009-80ст.
1

про публікацію авторської розробки
Додати розробку