Тотожні перетворення раціональних виразів
Тема. Тотожні перетворення раціональних виразів
Мета: домогтися засвоєння учнями змісту поняття «тотожні перетворення раціональних виразів» та схеми (алгоритму) перетворення раціонального виразу на раціональний дріб.
Тип уроку: засвоєння знань та первинних умінь.
Наочність та обладнання: опорний конспект «Тотожні перетворення раціональних виразів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Зібрати зошити учнів із виконаним домашнім завданням на перевірку.
Виконання вправи на повторення (виконання дій у виразі, що містить усі арифметичні дії з раціональними числами) обговорити під час фронтальної роботи (для пожвавлення можна організувати «математичну естафету» — змагання між учнями, які сидять на різних рядах).
III. Формулювання мети і завдань уроку
З метою усвідомленого сприйняття учнями слів учителя знову звертаємо їх увагу на те, що існує аналогія між способами перетворень суми, різниці, добутку і частки раціональних чисел та відповідно сумою, різницею, добутком і часткою раціональних виразів. Звернувшись до змісту останнього завдання домашньої роботи (знайти значення числового виразу, що містить всі дії з раціональними числами) та до попереднього міркування, формулюємо завдання — вивчення способів перетворення раціональних виразів, що містять кілька арифметичних дій різних ступенів із раціональними виразами.
Отже, формулювання мети уроку (вивчити питання про способи перетворення раціональних виразів, що містять кілька арифметичних дій) веде до усвідомлення необхідності формулювання і виконання завдань уроку:
• з'ясувати, чи відрізняється спосіб перетворення числових виразів від способів перетворення раціональних виразів;
• сформулювати загальну схему дій під час виконання вправ на перетворення раціональних виразів, що містять дії різних ступенів, на раціональний дріб;
• сформувати первинні вміння використовувати складену схему під час розв'язування відповідних вправ.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу перед його вивченням слід активізувати такі знання і вміння учнів: правила виконання арифметичних дій із раціональними числами та порядок виконання дій у числових виразах, що містять дії різного ступеня; тотожні перетворення цілих виразів; перетворення суми, різниці, добутку і частки двох раціональних дробів на раціональний дріб.
Виконання усних вправ
- При яких значеннях змінних дріб не має змісту?
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
При яких значеннях змінних цей дріб дорівнює нулю?
-
Подайте вираз у вигляді дробу: а)
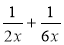 ; б)
; б) 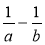 ; в)
; в) 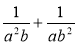 ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
- Які з рівностей є тотожностями. Чому?
а) 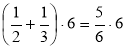 ; б)
; б) 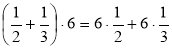 ;
;
в) 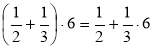 ; г)
; г) 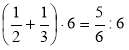 ?
?
V. Засвоєння знань
План вивчення нового матеріалу
- Загальне уявлення про можливість перетворення будь-якого раціонального виразу на раціональний дріб. Що означає фраза «спрости вираз»?
- Орієнтовна схема дій під час перетворення раціонального виразу на раціональний дріб.
|
Конспект 5 |
|
Тотожні перетворення раціональних виразів |
а) встановлюємо (визначаємо), які дії з раціональними дробами слід виконати, виходячи з умови завдання; б) виконуємо ці дії або у порядку спадання дії, або користуючись законами (властивостями) арифметичних дій (перестановка + і; сполучна + і; розподільна) та властивостями раціональних дробів (основною властивістю дробу) |
Мета вивчення останнього розділу «Перетворення раціональних виразів» підтеми «Множення і ділення раціональних дробів» полягає в узагальненні знань способів перетворення раціональних дробів та вмінь виконувати ці перетворення в комплексі. Тому вивчення теоретичного матеріалу слід розпочати із загального питання про можливість перетворення будь-якого раціонального виразу на раціональний дріб. При цьому вчителю слід наголосити на тому, що якщо завдання не ставиться інакше, то спрощення раціонального виразу вважається здійсненим, якщо в результаті тотожних перетворень дістали раціональний дріб (це твердження бажано проілюструвати низкою прикладів та контрприкладів). При цьому слід розуміти, що спрощення виразів (а саме так частіше формулюються завдання на перетворення раціональних виразів) не є якоюсь окремою арифметичною дією, завдання спростити вираз означає: по-перше, встановити, які дії і в якому порядку слід виконати за умовою виразу, а по-друге, правильно виконати ці дії у встановленому попередньо порядку.
Після цього переходимо до розгляду прикладів, уміщених у підручнику. При цьому бажано домогтися від учнів свідомого ставлення до цієї роботи: має бути фіксація послідовності дій та, можливо, створення узагальненої схеми дій під час виконання перетворень виразів подібною виду. Тому цю частину матеріалу уроку можна запропонувати учням для самостійного (або групового) опрацювання (за текстом підручника). У такому разі після самостійного опрацювання учнями нового матеріалу обов'язково проводиться презентація виконаної роботи, а за необхідності – корекційна робота.
VI. Засвоєння вмінь
Виконання усних вправ
-
Яка послідовність дій у виразі
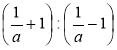 ?
?
-
Прокоментуйте виконання дій у виразі
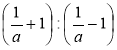 .
.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Відповідь. ![]() .
.
- Розкладіть на множники вираз:
а) тп – пk; б) т2п – тk; в) 9т2п – 6тk; г) т2 – п2; д) т2 – 1; є) т2 – 4n2;
ж) т3 – 4m; з) т3 + 8; и) m4 – 4m3 + 4m2.
Виконання письмових вправ
Для реалізації дидактичної мети уроку на цьому уроці слід розв'язати завдання такого змісту.
- Пряме застосування складеного на уроці алгоритму перетворення раціональних виразів на раціональний дріб.
1) Спростіть вираз:
а) 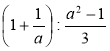 ; б)
; б) 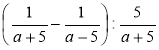 ;
;
в) ![]() ; г)
; г) 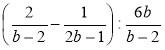 ;
;
д) ![]() ; є)
; є) 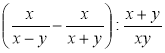 .
.
2) Виконайте дії:
а) 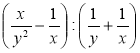 ; б)
; б) 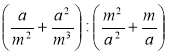 ;
;
в) ![]() ; г)
; г) 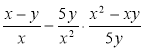 .
.
3) Виконайте дії: а) 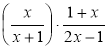 ; б)
; б) 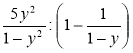 ;
;
в) 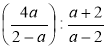 ; г)
; г) 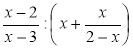 .
.
-
Обчислення значень виразів зі змінними при даних значеннях
змінних, що передбачають попереднє перетворення раціональних
виразів на раціональний дріб.
Спростіть вираз ![]() і знайдіть його значення при х = 6.
і знайдіть його значення при х = 6.
-
Доведення тотожностей із необхідністю виконувати перетворення
раціональних виразів на раціональний дріб.
1) Доведіть тотожність:
а) ![]() ; б)
; б) ![]() .
.
2) Доведіть тотожність:
а) 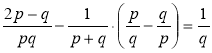 ;
;
б)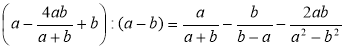 ;
;
в) 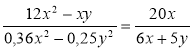 .
.
- Вправи на повторення.
1) Розв'яжіть рівняння: а) (х – 1)(х2 + х + 1) – х3 – х2 = 2х;
б) (х + 2)2 – 4 = 0; в) ![]() ; г)
; г) ![]() .
.
2) Із формули ![]() виразіть:
виразіть:
а) змінну с через змінні а і b; б) змінну b через змінні а і с.
-
Логічні вправи та завдання підвищеного рівня складності для учнів,
які мають достатній та високий рівні знань.
1) Доріжкою велотреку їдуть два велосипедисти зі сталими швидкостями. Коли вони їдуть у протилежних напрямках, то зустрічаються через кожні 10 с; коли ж в одному напрямку, то один наздоганяє іншого через кожні 100 с. Яка швидкість кожного велосипедиста, якщо довжина доріжки 200 м?
2) Доведіть, ідо якщо m ≠ n, m ≠ 0 і n ≠ 0, то значення виразу
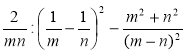 не залежить від значень змінних.
не залежить від значень змінних.
3) Яке число пропущене?
|
|
- 3 |
|
|
? |
Розв'язуючи вправи (див. вище) на перетворення раціональних виразів, необхідно спеціально зупинятись на першому пункті схеми перетворень раціональних виразів — на порядку виконання перетворень, бо саме на цьому етапі учні припускаються найбільшої кількості помилок. Тому корисно перед початком розв'язування письмових завдань розібрати кілька усних вправ на визначення порядку виконання дій у числових виразах.
Слід зауважити, що всі вправи, спрямовані на формування вмінь перетворення раціональних виразів, є досить складними для учнів, бо передбачають упевнене оволодіння одночасно всіма алгоритмами перетворень раціональних дробів. Тому бажано диференціювати вимоги до темпу та кількості розв'язаних завдань для учнів з різними рівнями навчальних досягнень. Щоб попередити можливі помилки (особливо в учнів, які потребують додаткової педагогічної уваги), можна широко використовувати довідковий матеріал (картки-підказки, довідкові таблиці тощо).
Щоб урізноманітнити урок, присвячений формуванню оперативних навичок, слід включати до розгляду завдання на повторення.
VII. Підсумки уроку
В якому з випадків правильно вибрана послідовність дій із раціональними виразами?
а) 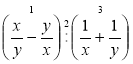 ; б)
; б) 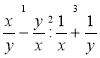 ; в)
; в) 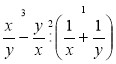 .
.
VIII. Домашнє завдання
- Вивчити орієнтовну схему дій перетворення раціонального виразу на раціональний дріб.
- Розв'язати вправи на застосування вивченої схеми.
- Повторити: зміст поняття рівняння з однією змінною, лінійне рівняння з однією змінною та супутні поняття (див. довідник з математики, 7 клас), умову рівності раціонального дробу до нуля, а також розв'язати відповідні вправи.


про публікацію авторської розробки
Додати розробку
