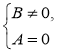Раціональні рівняння. Розв'язування раціональних рівнянь

Тема. Раціональні рівняння. Розв'язування раціональних рівнянь

Мета: домогтися засвоєння учнями змісту понять: «раціональне рівняння», «ціле раціональне рівняння», «дробово-раціональне рів­няння» - та усвідомлення логічного зв'язку між цими поняттями; сформувати в учнів уявлення про зміст поняття «ОДЗ рівняння», роль його в побудові загальної схеми розв'язання дробово-раціонального рівняння та про саму схему розв'язання дробово-раціонального рів­няння; сформувати вміння відрізняти вивчені види рівнянь одне від одного та аргументувати свою думку; знаходити, використовуючи зміст поняття, ОДЗ рівняння, а також розв'язувати найпростіші дробово-раціональні рівняння за вивченою схемою.

Тип уроку: засвоєння знань та первинних умінь.

Наочність та обладнання: опорний конспект «Раціональні рівняння».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Перевірку домашнього завдання проводимо як аналіз самостійної роботи (див. попередній урок).

III. Формулювання мети і завдань уроку

На інтуїтивному рівні учні мають первинне уявлення про структуру шкільного курсу алгебри. Цю інформацію вчитель міг надати учням раніше, ще на початку вивчення алгебри, або на одному з уроків система­тизації та повторення матеріалу, вивченого у 7 класі, або запропонувати схему, то відображує структуру шкільного курсу алгебри 7—9 класу.

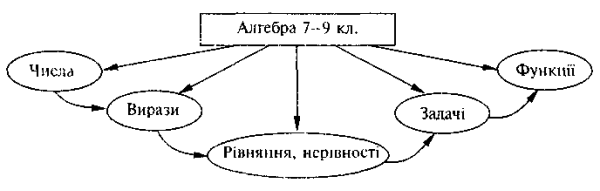
Тому вони мають усвідомити той факт, що вивчення способів перетворення самих по собі раціональних виразів не с самоціллю ви­вчення алгебри, навпаки, вони цікавлять нас лише тому, що можуть бути застосовані в роботі з іншими об'єктами вивчення алгебри – рівняннями (та нерівностями), які у свою чергу є засобом для розв'язу­вання текстових задач. Тому цілком логічно після вивчення способів перетворень дробових раціональних виразів вивчити питання про види та способи розв'язання рівнянь, що складаються з таких виразів. Ці слова вчителя висловлюють основну дидактичну мету уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняті учнями навчального матеріалу перед вивченням матеріалу уроку слід активізувати такі знання і вміння учнів: означення цілих та дробових раціональних ви­разів, тотожних перетворень цілих виразів та раціональних дробів (перетворень суми, різниці, добутку і частки двох раціональних дробів на раціональний дріб), а також умови рівності дробу нулю, ОДЗ раціонального (цілого та дробового виразів) та основної властивості пропорції; змісту основних по­нять, пов'язаних із поняттям рівняння з однією змінною (ко­рінь рівняння або розв'язок рівняння, що означає розв'язати рівняння з однією змінною)

Виконання усних вправ

1. Обчисліть: ; ; ; ; ; ; ; .
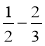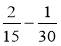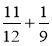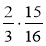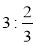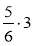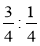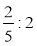2. Укажіть допустимі значення змінної у виразі:

х² – 4; ; ; ; ; .

При яких значеннях змінних вирази набувають значення, що до­рівнює нулю?

3. Назвіть порядок виконання дій у виразі:

а) 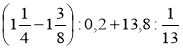; б) ; в) .

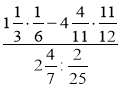4. Подайте вирази у вигляді нескоротного дробу:

а) ; б) ; в) ; г) ; д) .

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення раціонального рівняння, цілого раціонального рівнян­ня, дробово-раціонального рівняння (із прикладами та контрприкладами).

2*. Означення   ОДЗ   (раціонального)   рівняння;   знаходження   ОДЗ раціонального рівняння.

3. Алгоритм розв'язання дробово-раціонального рівняння виду = 0, (де А і В — деякі многочлени від однієї змінної).

4. Приклад застосування вивченого алгоритму.

5*. Схема розв'язання найпростіших дробово-раціональних рівнянь з параметром.

 Вивчення матеріалу уроку починається з систематизації знань учнів щодо видів рівнянь з однією змінною та доповнення знань учнів про види рівнянь уявленням про загальний вид раціональних рівнянь, а також різновидів таких рівнянь (цілих та дробових). При цьому важливо, щоб учні усвідомили, що саме вид виразів, з яких складається дане рівняння, і визначає вид рівняння, який у свою чергу визначає спосіб розв'язання рівняння.

На цьому уроці розпочинається копітка робота з формування сталих умінь учнів розв'язувати дробові рівняння шляхом рівносильних пере­творень, за загальною схемою, поданою в «Таблицях з алгебри, 7—11 кла­си» Є. П. Неліна, яка передбачає передусім розуміння учнями змісту поняття «ОДЗ рівняння». Тому для формування в учнів уміння матема­тично грамотно розв'язувати дробові рівняння правильно було б уже на перших уроках знайомства учнів із новим для них видом рівнянь, відштовхуючись від знайомого учням поняття ОДЗ виразу, сформувати означення ОДЗ рівняння і на прикладах продемонструвати, як впливає зміна ОДЗ (перехід від цілого рівняння до дробового) на кількість та можливість існування коренів рівняння (такий підхід до викладення пи­тання про розв'язування дробово-раціональних рівнянь у 8 класі до­цільно здійснювати за умови належного рівня інтелектуальної підготов­ки учнів). Далі доцільно було б скласти з учнями алгоритм знаходження ОДЗ найпростішого дробового раціонального рівняння виду

= 0

(де А і В — деякі многочлени від однієї змінної).

У 8 класі традиційно вивчається кілька способів рівносильного перетворення дробових рівнянь, але на першому уроці, щоб не перевантажити учнів новими поняттями, до розгляду пропонується спосіб розв'язання дробових рівнянь, який передбачає використання умови рівності дробу нулю.

* Якщо дозволяє рівень підготовки учнів (сформовані чітке уявлен­ня про зміст поняття рівняння з параметром та вміння розв'язувати лінійні рівняння з параметрами), то вже на цьому уроці можна запро­понувати учням ознайомитись зі схемою розв'язання дробово-раціо­нальних рівнянь із параметром.

VI. Засвоєння знань

Виконання усних вправ

1. Які з рівнянь: 2х – 1 = 0; х² – 3х + 5 = 0; 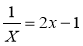; ; 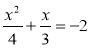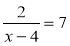є раціональними? цілими раціональними? дробово-раціональними?
2. Прокоментуйте (використовуючи алгоритм) розв'язання рівняння .

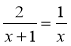1) ОДЗ: х ≠ 0 та х + 1 ≠ 0; х ≠ 0 та х ≠ -1;

2) , , ;

3) х – 1 = 0,

    х = 1 — входить до ОДЗ.

Відповідь. 1.

3. Заповніть таблицю:

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1*. Знаходження ОДЗ дробово-раціонального рівняння виду = 0, де А і В — деякі многочлени від однієї змінної.

2. Перевірка за відомим ОДЗ рівняння, які із заданих чисел не є коре­нями рівняння (не входять до ОДЗ).

3. Розв'язування дробово-раціональних рівнянь виду = 0 (де А і В — деякі многочлени від однієї змінної) за алгоритмом (див. вище).

1) Розв'яжіть рівняння: а) ; б) ; в) .

2) Розв'яжіть рівняння: а) ; б) ; в) .

3) Розв'яжіть рівняння: а) ; б) ; в) .

4. Складання та розв'язування рівнянь за словесним описом.

1) Яке число треба додати до знаменника дробу , щоб дістати дріб ?

2) Яке одне й те саме число треба додати до чисельника дробу і помножити на нього знаменник цього дробу, щоб дістати дріб ?

5. Складання та розв'язування рівнянь за умовою задачі.
Знаменник дробу на 3 більший від чисельника. Якщо до чисельни­ка дробу додати 32, то дістанемо дріб, удвічі більший від даного.
Знайдіть початковий дріб.

6*. Розв'язування дробово-раціональних рівнянь з параметром.

Розв'яжіть рівняння з параметром а: .

7. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) При якому значенні а тотожно рівні вирази і ?

2) Яке число пропущене?

8. На повторення: перетворити раціональний вираз із використанням набутих раніше знань.

Спростіть вираз:

а) ;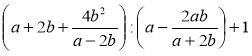

б) ;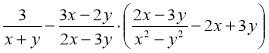

в) ;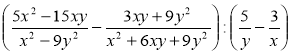

г) .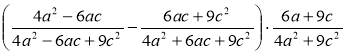

 Вправи для письмового розв'язування, запропоновані на урок, передбачають формування вмінь використовувати алгоритм роз­в'язання дробово-раціональних рівнянь, розглянутий вище, тому представляють досить велику кількість раціональних рівнянь; але, щоб урізноманітнити роботу учнів на уроці, вправи на розв'язування рівнянь можна доповнити вправами на скла­дання рівнянь або за описом співвідношення виразів, з яких складається рівняння (на цьому етапі можна провести роботу зі складання всіх можливих видів рівнянь для даного запису співвідношення виразів), або за умовою арифметичної задачі. Також вправи уроку можна доповнити вправами на повторення попереднього матеріалу (перетворення раціональних виразів).

 *Якщо дозволяє рівень підготовки учнів (з метою довгостроко­вої підготовки до незалежного зовнішнього оцінювання учнів у 12 класі), можна запропонувати до розв'язування серію най­простіших дробово-раціональних рівнянь із параметром (ви­вчивши попередньо відповідний алгоритм).

VII. Підсумки уроку

В якому з випадків правильно розв'язане рівняння?

VIII. Домашнє завдання

1. Вивчити означення раціонального рівняння, цілою раціонального рівняння, дробово-раціонального рівняння, ОДЗ раціонального рівняння, алгоритм розв'язання дробово-раціонального рівняння виду 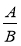= 0, (де А і В – деякі многочлени від однієї змінної).
2. Розв’язати вправи на застосування вивченого алгоритму різного рівня складності.
3. Повторити властивості рівносильних рівнянь, основну властивість пропорції; розв'язали серію рівнянь на застосування цих власти­востей (див. 6, 7 класи).