Тотожні перетворення раціональних виразів
Тема. Тотожні перетворення раціональних виразів
Мета: закріпити знання учнів про загальну схему дій під час перетворення раціонального виразу на раціональний дріб; доповнити знання учнів деякими спеціальними видами перетворень раціональних виразів (способи перетворення відношення двох дробових виразів, способи перетворення раціональних виразів із застосуванням властивостей арифметичних дій); удосконалювати вміння учнів виконувати тотожні перетворення раціональних виразів за загальною схемою та із застосуванням спеціальних способів перетворень.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Тотожні перетворення раціональних виразів».
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
Щоб зекономити час на уроці, вчитель може запропонувати учням роздавальний матеріал — розв'язання домашніх вправ на перетворення раціональних виразів із повним розв'язанням — самостійно опрацювати, у класі перевіряється правильність виконання запропонованих завдань; роботи учнів, що не мають помилок, можна оцінити.
Більш ретельно можна перевірити виконання завдання на повторення (включивши вправи на повторення до усних вправ (див. нижче)).
III. Формулювання мети і завдань уроку
З метою більш глибокого усвідомлення учнями необхідності вивчення питання уроку (вивчення деяких прийомів «швидкого» перетворення раціональних виразів) можна вкотре звернутись до аналогічних прийомів перетворень числових виразів, вивчених у 6 класі. Для цього пропонуємо учням виконати завдання 1.
Завдання 1
Обчисліть значення виразу найбільш раціональним способом:
а) 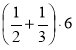 ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 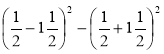 .
.
Після обговорення виконуємо дії та знову акцентуємо увагу учнів на тих властивостях, застосування яких дозволило суттєво спростити обчислення; після чого пропонуємо учням завдання 2.
Завдання 2
Спростіть раціональні вирази (подібні за формою до розв'язаних числових виразів).
а) 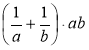 ; б)
; б) 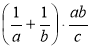 ; в)
; в) ![]() ; г)
; г) 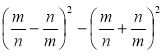 .
.
Під час обговорення формулюємо питання: «Чи можна використовувати під час перетворення раціональних виразів властивості дій над числами та властивості самих раціональних виразів, щоб спростити процедуру перетворення раціонального виразу на раціональний дріб?»
Зрозуміло, що пошук відповіді на поставлене питання і є основною дидактичною метою уроку.
IV. Актуалізація опорних знань та вмінь
Як і на попередньому уроці, з метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння учнів: правила виконання арифметичних дій із раціональними числами та порядок виконання дій у числових виразах, то містять дії різного ступеня; тотожні перетворення цілих виразів; перетворення суми, різниці, добутку і частки двох раціональних дробів на раціональний дріб; знаходження найменшого спільного знаменника для кількох раціональних дробів, а також застосування розподільної властивості множення відносно додавання для спрощення обчислень (значень числових виразів).
Виконання усних вправ
- Розкажіть про порядок виконання перетворень виразу
![]()
або запишіть цей порядок, якщо взяти в дужки вирази: ![]() ;
; ![]() ;
; ![]() . Чому?
. Чому?
-
Яке число (вираз) слід поставити замість *, щоб утворена рівність
була тотожністю?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 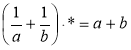 .
.
-
Знайдіть спільний знаменник для дробів:
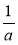 і
і 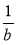 ;
; 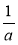 ,
, 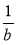 і
і 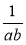 ;
; 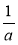 ,
, 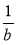 і
і 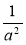 ;
; 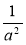 і
і 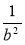 ; 1 і
; 1 і 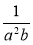 .
.
V. Засвоєння знань
План вивчення нового матеріалу
- Застосування розподільної властивості множення для перетворень раціональних виразів.
- Застосування основної властивості дробу для перетворень раціональних виразів.
- Застосування для перетворення раціональних виразів алгоритмів перетворень цілих виразів (формул скороченого множення, розкладання на множники тощо).
Навчальний матеріал цього уроку, як і будь-який інший матеріал, пов'язаний із раціоналізацією перетворень, передбачає вільне оволодіння учнями змістом навчального матеріалу попередніх уроків і наявності достатнього та високого рівнів умінь учнів щодо застосування цих знань на практиці. Тому, перш ніж переходити до вивчення раціональних способів перетворення раціональних виразів, учитель має переконатися, що учні готові сприймати цей матеріал (в іншому випадку він переноситься на наступний урок або дається фрагментарно і оволодіння ним не вимагаємо від усіх учнів).
Якщо учні готові до сприйняття цього навчального матеріалу, тоді прийоми «швидких перетворень» краще за все вивчати на конкретних прикладах, супроводжуючи їх коментарем. Особливу увагу слід приділити перетворенню так званих «чотириповерхових дробів» (тобто відношень двох дробових виразів) та їх особливих випадків, бо, як відомо з досвіду роботи, ці перетворення є найскладнішими для розуміння учнями. Тому дуже важливо перед початком роботи з вивчення перетворень такого виду виконати відповідні вправи на повторення (знайти спільний знаменник для дробів та виконати множення раціонального дробу на цілий вираз), що й відбувається під час виконання усних вправ.
VI. Засвоєння вмінь
Виконання усних вправ
- Прокоментуйте правильність виконаних дій у виразах:
а) ![]() ;
;
б) 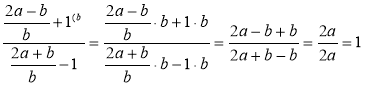 .
.
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту.
- Спрощення раціональних виразів із використанням, де це можливо, розподільної властивості множення відносно додавання (віднімання).
1) Спростіть вираз:
а) 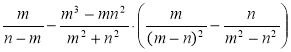 ; б)
; б)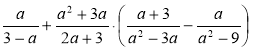 .
.
2) Спростіть вираз:
а) 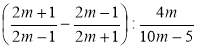 ; б)
; б) 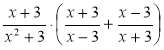 .
.
-
Спрощення виразів із використанням (якщо це доцільно) формул
скороченого множення або інших способів розкладання многочленів на множники.
1) Подайте у вигляді многочлена чи раціонального дробу:
а) 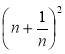 ; б)
; б) 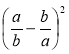 ; в)
; в) 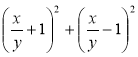 ; г)
; г) 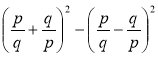 ;
;
д) 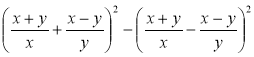 ; є)
; є) 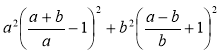 .
.
-
Спрощення виразів, що мають вигляд відношення двох дробових
виразів, із використанням основної властивості дробу.
1) Спростіть вираз: а) 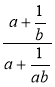 ; б)
; б) 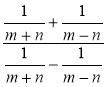 .
.
2) Спростіть вираз: а) ![]() ; б)
; б) 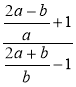 ; в)
; в) 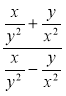 ; г)
; г) 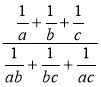 .
.
3) Виконайте підстановку та спростіть здобутий вираз:
а) ![]() , якщо
, якщо ![]() ; б)
; б) ![]() , якщо
, якщо ![]() .
.
-
Знаходження ОДЗ виразу (або, навпаки, значень змінних, при яких
дріб не має змісту); знаходження, значень змінних, при яких вираз
дорівнює нулю.
1) При яких значеннях змінної не мас змісту вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ?
?
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Спростіть вираз:
а) 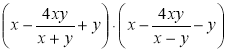 ; б)
; б) 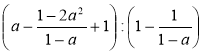 .
.
2) Доведіть тотожність: 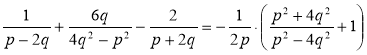 .
.
3) Доведіть тотожність Л. Ейлера: 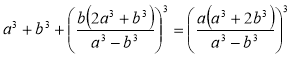 .
.
4) Яке число пропущено?
|
у = 4х + b |
у = -х + а |
|
|
|
|
-13 |
9 |
Формуванню сталих навичок перетворень раціональних виразів із використанням властивостей арифметичних дій та властивостей раціональних дробів сприяє виконання достатньої кількості різних за змістом вправ. Але, крім цього, слід приділити увагу й розгляду питань на повторення (особливо це стосується матеріалу про ОДЗ раціонального виразу та умови, що дріб дорівнює нулю, — цей матеріал необхідно повторити з метою успішного сприйняття питання розділу — «Раціональні рівняння»).
VII. Підсумки уроку
В якому з випадків правильно виконано дію з раціональними дробами?
а) 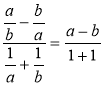 ; б)
; б) 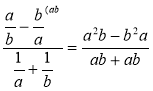 ;
;
в) 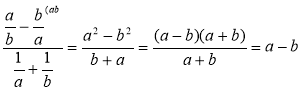 .
.
VIII. Домашнє завдання
- Засвоїти зміст вивчених способів перетворень раціональних виразів.
- Розв'язати вправи на застосування цих способів.
- На повторення: вправи на знаходження ОДЗ виразу та використання умови, що дріб дорівнює нулю, завдання, що передбачають розв'язування лінійних рівнянь.


про публікацію авторської розробки
Додати розробку